基于遺傳算法的鐵路縱斷面優化研究
何祥衛
(中鐵第四勘察設計院集團有限公司,湖北武漢 430063)
在解決鐵路縱斷面優化問題時,首先要建立基于優化算法的數學模型,所以優化算法不單單會對模型的質量產生影響,而且也決定了該模型求解的精度和效率。當前國內應用廣泛的算法主要有蟻群算法、二次規劃法、梯度投影法等。蟻群算法由 M.Dori于1991年提出[1],它主要應用于離散空間優化問題,之后很多研究人員對該算法進行改進以適于解決連續性的鐵路線路優化問題,但它還不是真正意義上的連續空間優化。二次規劃法是一種特殊的非線性規劃方法,缺點是以二次函數作為目標函數的海森矩陣很難求得。梯度投影法適用于解決具有線性約束的非線性規劃問題[2],它的弊端是當優化過程接近最優解時,“鋸齒”現象頻繁發生,從而導致收斂速率下降,最優解難以得到。針對上述方法存在的問題,本文引入遺傳算法,此方法可在一個可行域中自動搜索一個最優解或較優解[3,4],且對求解問題限制較少,可適用于解決傳統搜索方法難以處理的縱斷面優化問題。
1 建立縱斷面優化的數學模型
1.1 優化變量
整個縱斷面設計線可由變坡點里程、變坡點的設計高程和相應的豎曲線表達,依照遺傳算法搜索求解過程的全局性,筆者在此選取變坡點里程和變坡點的設計高程這兩個優化變量,采用改進后的遺傳算法進行優化研究。
1.2 目標函數
傳統的縱斷面優化模型是在縱斷面線路設計要素滿足適當的約束條件下,盡可能地節約人力物力,減少工程造價成本,所以應把線路的總工程費用作為目標函數進行優化。考慮到實際工程包含路基土石方工程、橋隧工程、支擋工程、涵洞工程等分項工程,將它們分別設立不同的目標函數,并作表達式如下

式中,f1(x)為路基土石方工程費用;f2(x)為橋隧工程費用;f3(x)為支擋工程費用;f4(x)為涵洞工程費用;f(x)為縱斷面設計線的總工程費用。
1.3 約束條件
縱斷面設計的約束條件包括:坡度約束、坡長約束、起終點高程約束、豎緩曲線重疊約束、平縱組合約束等。
2 基于遺傳算法的縱斷面優化設計
遺傳算法是一種模擬自然選擇和生物進化機制的優化算法。1975年,美國的John Holland教授首次提出該算法,它的基本思想來源于達爾文的進化論和Mendel的遺傳學說[5]。遺傳算法中核心的兩個算子是交叉和變異,它們被反復利用到由可以代表問題的解的染色體上。遺傳算法基于適應度函數選擇合適的染色體,并剔除掉適應性較差的染色體,按照適者生存的原則,通過交叉變異的反復迭代過程產生適應環境的新種群[6,7]。下面對基于遺傳算法的縱斷面優化模型進行分析闡述。
2.1 編碼設計
常見的編碼方式是Holland教授提出的二進制編碼。為了更好地結合縱斷面優化的知識建立模型,本文采用實數編碼方式。該編碼適用于較大空間的搜索,能解決變坡點位置組合需要較大空間搜索的問題,并將編碼的基因與變坡點一一對應起來,能有效提高該模型的精度和效率。
實數編碼中每個個體ρ可表示為
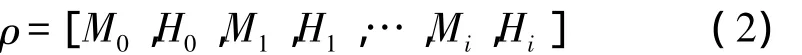
式中,Mi為變坡點里程,Hi為變坡點設計高程,i=1,2,3,…,n。
2.2 種群初始化
為了使初始種群具有多樣性,減少算法陷入局部解的可能性,本文將采用崎嶇度的方法對初始個體進行處理,并挑選最優個體放入初始種群,從而得到適合算法的初始種群[8]。這種方法能使模型在預期內得到最優解,并且能縮減搜索時間。
縱斷面方案的初始種群是一系列由崎嶇度生成的個體的集合,每個個體分別代表一組解,即一條完整的經連續處理后的縱斷面曲線。
2.3 適應度函數的構建
遺傳算法進化過程以每個個體的適應度值作為選擇依據。縱斷面優化的目標是減少線路運營維護費用以及增強機車行駛安全性,并且改良與周邊環境的協調性(平面線型已經擬定的情況)。但是現階段研究尚未明確揭示線路運營維護費用與縱斷面線形之間的關系,而且線路與周邊環境的協調性也不好量化。在此選取土石方工程費用作為適應度函數變量,基于此目標函數求得個體的適應度值。
要選取遺傳進化過程中最優的個體,則需根據土石方費用函數建立適應度函數,計算個體的適應度值,然后將個體的適應度值進行排列選擇。該適應度函數如下
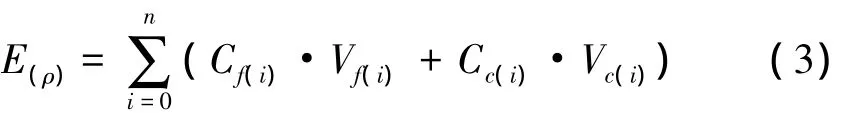
式中,n為方案中橫斷面的個數;Vf(i)、Vc(i)分別為i路段的填、挖體積;Cf(i)、Cc(i)分別為i路段的單位填方及挖方費用。
2.4 遺傳操作數
標準遺傳算法操作數包含選擇、交叉和變異。這3個操作數分別模擬了自然界中生物進化的3個不同階段,同時這3個階段也是相互結合相互滲透的。因此,選擇合適的或者改變每個算子的排列組合和操作方式,都能極大程度地影響該算法的優化計算結果。
2.4.1 選擇策略
在保持種群多樣性的前提下為使得算法收斂速度加快,本文采用排序輪盤法選擇算子。第一步計算每個個體的適應度值 E(ρi),其中 i=1,2,…,n,然后對種群中的個體按照其適應度值E(ρi)由小到大排列。選擇每個個體ρ的概率pi為

計算個體ρ的累積概率qi為

旋轉n次輪盤后,獲得新的種群。輪盤方法中放回取樣的選擇策略容易使新種群產生重復的方案,所以在該過程中,要對重復的新方案進行剔除。選擇策略設計流程如圖1所示。
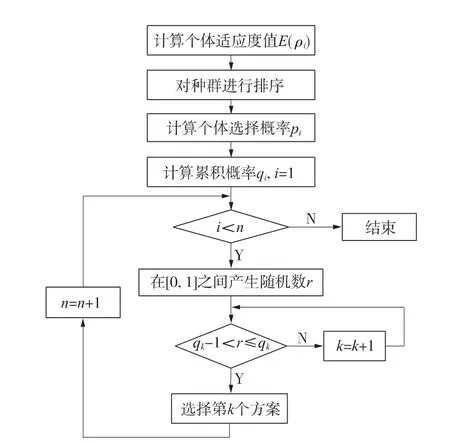
圖1 選擇操作流程
2.4.2 交叉操作
交叉算子是遺傳算法中最核心的部分,即把2個配對的染色體在同一位置被切斷,基因重組后形成2個新個體。通過交叉操作產生的個體具有離散性強的特征,該特征能夠大大增強算法的全局尋優能力。本文采用啟發式交叉,將適應度較大的個體向著較優的個體增大的方向移動,交叉后得到更優個體。該交叉方法有利于生成較優個體,能在全局范圍內搜索變坡點。
2.4.3 變異操作
變異運算是對個體串的某些基因值做等位替換后形成一個新個體。根據已有經驗,優化設計中交叉采用多種變異算子。變異概率Pm通常取0.000 1~0.1。通過變異操作,計算種群中的最優的縱斷面方案(即最優個體)與當前個體的差異值,將該值乘以變異概率來調整當前縱斷面方案。
2.5 約束條件的處理
上文已經介紹了縱斷面設計的約束條件,經過每次迭代后產生新的個體,若個體符合約束條件,則保留用于下一次迭代,若不符合,則剔除并重新迭代。
2.6 停止規則
利用遺傳算法進行縱斷面優化的目標是為了尋得可行解中的最優方案,并且該方案能滿足事先設定的所有約束條件。上述過程已經完成了一次完整的迭代,是否繼續取決于算法的停止規則。一種是指定一個最大的遺傳代數G,當進化迭代次數達到G時即停止;另一種是對各代的最佳解進行監控的方法,動態確定停止規則。即當前的最好解在連續20代沒有變化時即停止計算。否則,將繼續迭代。在本文中采用后一種方法。
3 算法實現過程
基于遺傳算法與動態監測最優解的方法需要通過許多次的迭代才能不斷地接近最優解,該過程用人工計算幾乎不可能實現。本文為解決該算法繁瑣冗長的計算過程,在VS.NET下利用AutoCAD二次開發平臺和遺傳算法方法編制了縱斷面優化程序,以期提高程序的執行效率。縱斷面優化程序流程如圖2所示。
4 結語
本文引進了模擬生物進化過程和遺傳機理的遺傳算法,該算法具有全局優化和對問題提供啟發式等特點,將遺傳算法應用于縱斷面優化模型,能更便捷地解決多峰函數優化問題以及無解析表達式的目標函數優化問題,提高優化模型的計算效率,減少設計人員的工作任務量,具有很好的適用價值。但是,遺傳算法的應用依然存在一些適應度函數及有效約束處理上的問題,在接下來的研究中,應重點考慮改進遺傳算法的構造方式。
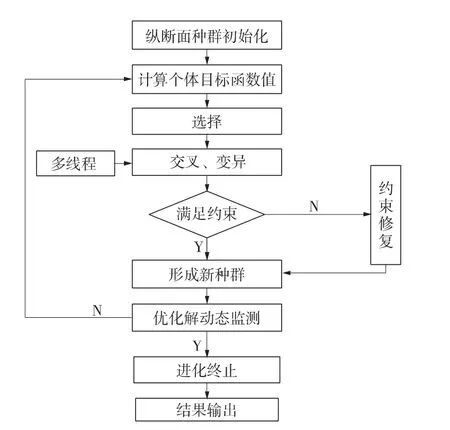
圖2 縱斷面優化程序流程
[1]段海濱.蟻群算法原理及其應用[M].北京:科學出版社,2005.
[2]詹振炎.梯度投影法及其在鐵路縱斷面設計中的應用[J].長沙鐵道學院學報,1979,26(4):32-37.
[3]Eungcheol Kim,Manoj K.Jha,Bongsoo Son.Improving the computational efficiency of highway alignment optimization models through a stepwise genetic algorithms approach[J].Transportation research part B,2005,17(39):339-360.
[4]Goldberg,D.E.Genetic Algorithms in Search,Optimization,and Machine Learning[M].Massachusetts,Addison-Welsey Publishing Company Inc,1989.
[5]楊獻波.基于遺傳算法的公路縱斷面優化研究[D].南京:東南大學,2006.
[6]陳國良.遺傳算法及其應用[M].北京:人民郵電出版社,1996.
[7]李敏強.遺傳算法的基本理論與應用[M].北京:科學出版社,2002.
[8]許金良.集成化公路CAD系統研究與開發[D].西安:長安大學,2002.

