基于橢球不確定集約束的魯棒自適應相干檢測器
代保全 王 彤 同亞龍 吳建新 保 錚
?
基于橢球不確定集約束的魯棒自適應相干檢測器
代保全 王 彤*同亞龍 吳建新 保 錚
(西安電子科技大學雷達信號處理國家重點實驗室 西安 710071)
針對存在導向矢量誤差時自適應相干檢測器(ACE)的檢測性能下降問題,該文提出一種基于橢球不確定集約束的魯棒ACE設計方法。該方法在深入分析ACE檢測器工作原理的基礎上,利用導向矢量的尺度變化不影響ACE檢測器輸出這一特點,建立魯棒ACE檢測器模型并將其轉化為凸優化問題,最后采用牛頓-拉夫森方法對該問題進行求解。仿真實驗結果表明,該方法可有效提高ACE檢測器對導向矢量誤差的魯棒性。
雷達信號處理;自適應相干檢測器;導向矢量誤差;橢球不確定集;魯棒檢測
1 引言
上述方法所建立的導向矢量模型與導向矢量的尺度有關,而ACE檢測器與導向矢量的尺度無關,因此并不適用于改善ACE檢測器對導向矢量誤差的敏感性。針對這種情況,本文給出了一種魯棒ACE檢測器的設計方法。首先假設真實導向矢量位于一橢球不確定集[14]內,然后根據ACE檢測器的特點,將魯棒ACE設計問題轉化為凸優化問題,最后采用牛頓-拉夫森方法求解該優化問題。本文方法適用于包括波束指向誤差以及陣元幅相誤差在內的多種導向矢量誤差情況,仿真實驗驗證了該方法的有效性。
2 信號模型
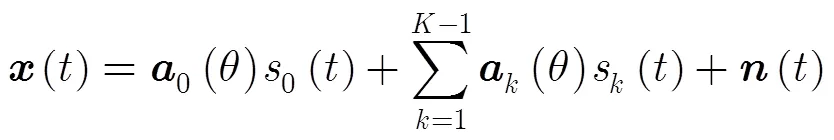
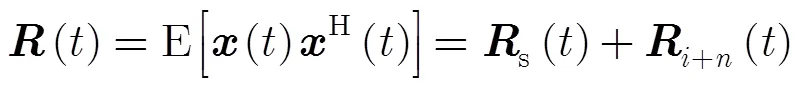

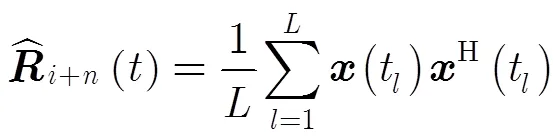
經整理后,式(3)可以寫成式(5)形式[1,2]:
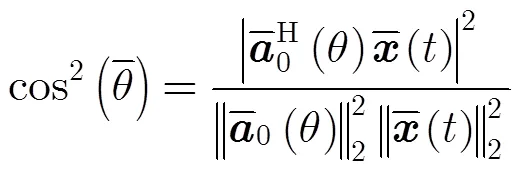
實際上,式(3)也可以表示成式(6)形式:
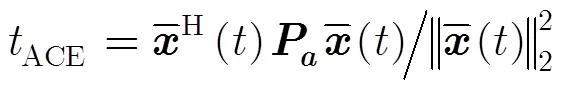
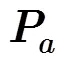
3 魯棒ACE檢測器算法原理
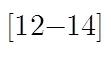
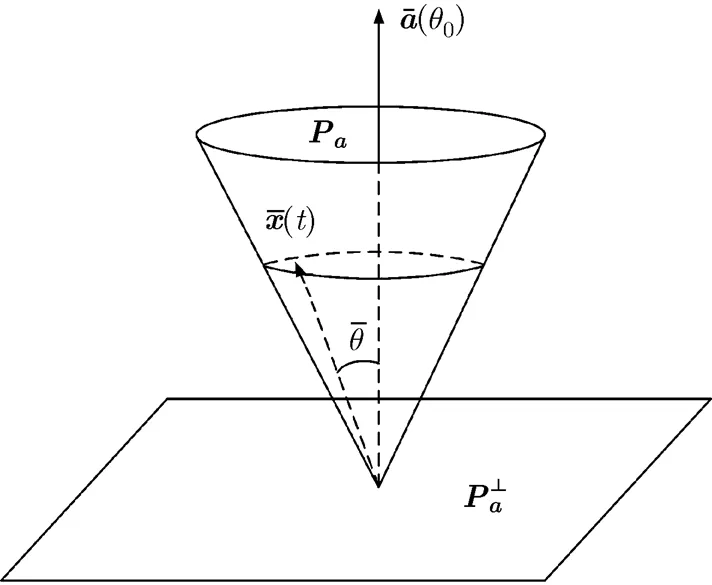
圖1 ACE檢測器示意圖
3.1算法提出

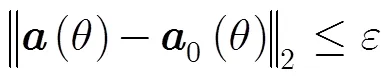


則式(9)中的橢球不確定集約束可以轉化為如式(11)的球不確定集約束。
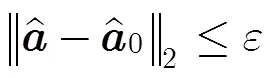
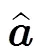
則式(11)可轉化為式(12):

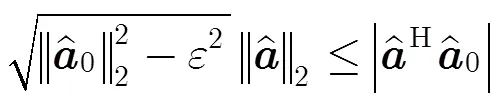



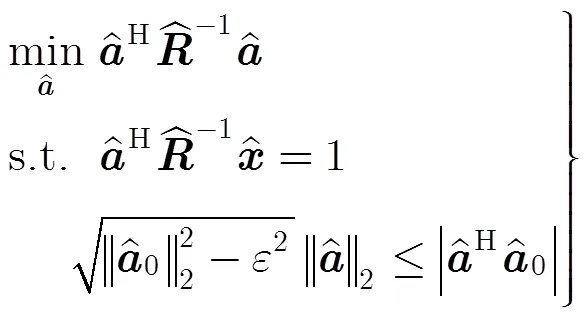
這里,我們采用Lagrange乘子算法[13,14]對式(16)進行求解。
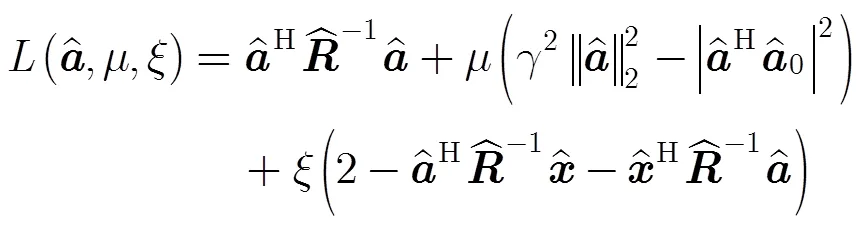
對式(17)進行整理有
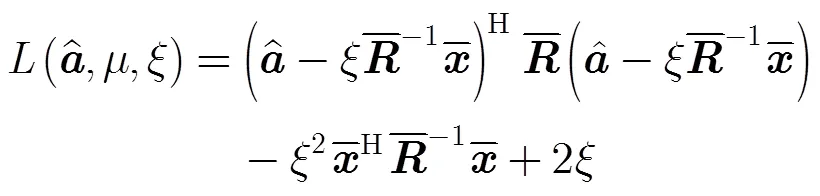
顯然,如果滿足


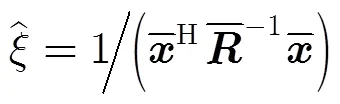
將式(21)代入式(20)有

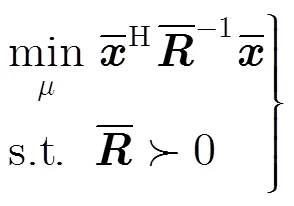
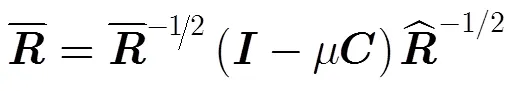
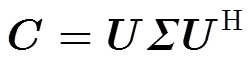
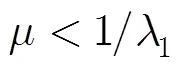

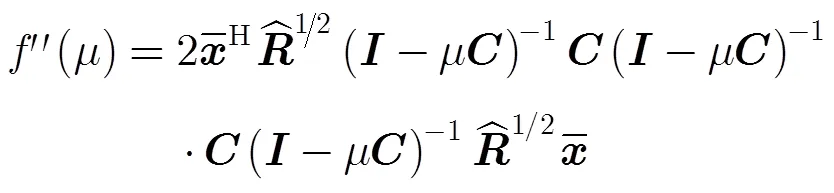
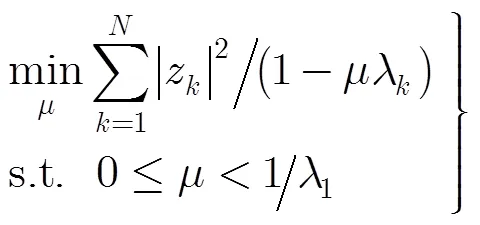
3.2算法實施步驟
本文算法的實施步驟總結如下:
步驟1 利用式(10)將橢球不確定集約束轉化為球不確定集約束。
3.3運算量分析

4 仿真分析
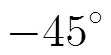
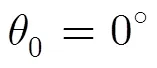

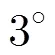
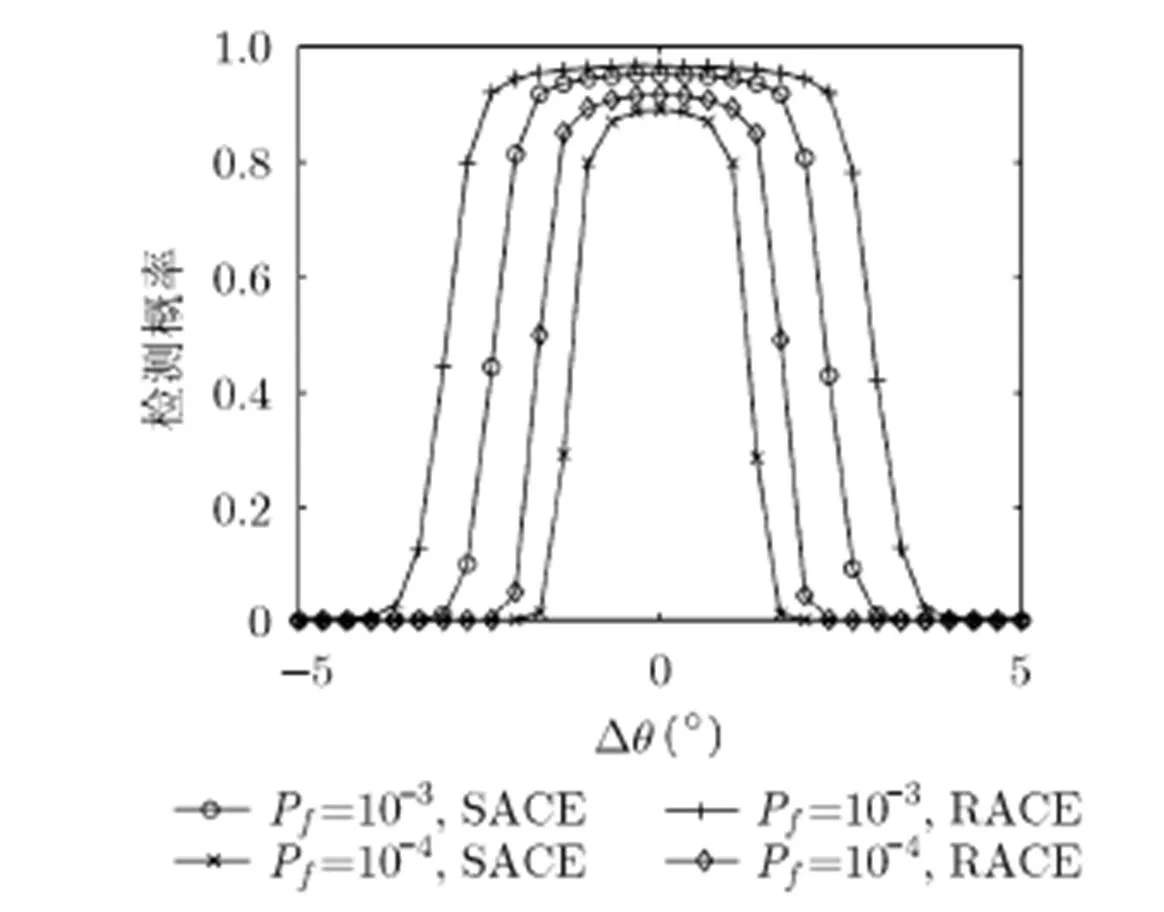
圖3 檢測概率隨指向誤差的變化情況
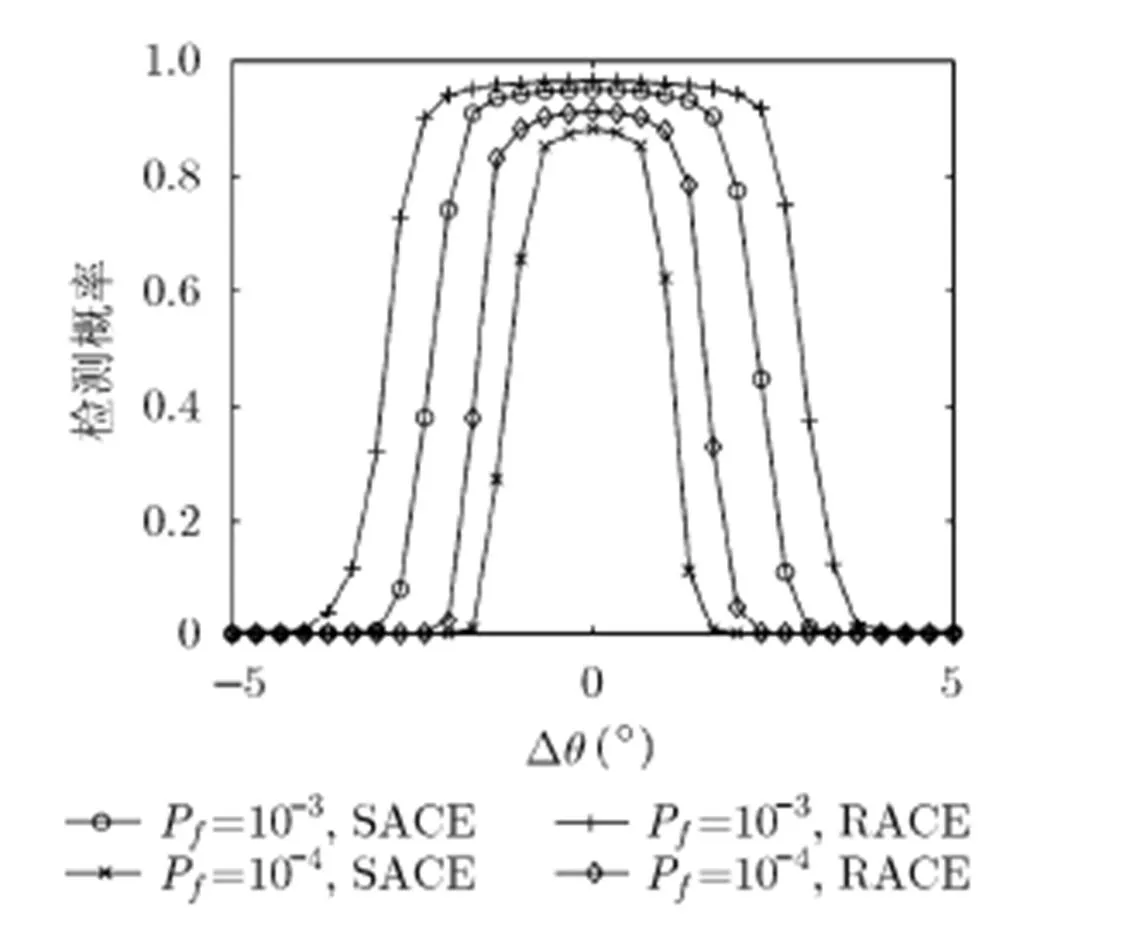
圖4 存在幅相誤差時,檢測概率隨指向誤差的變化情況
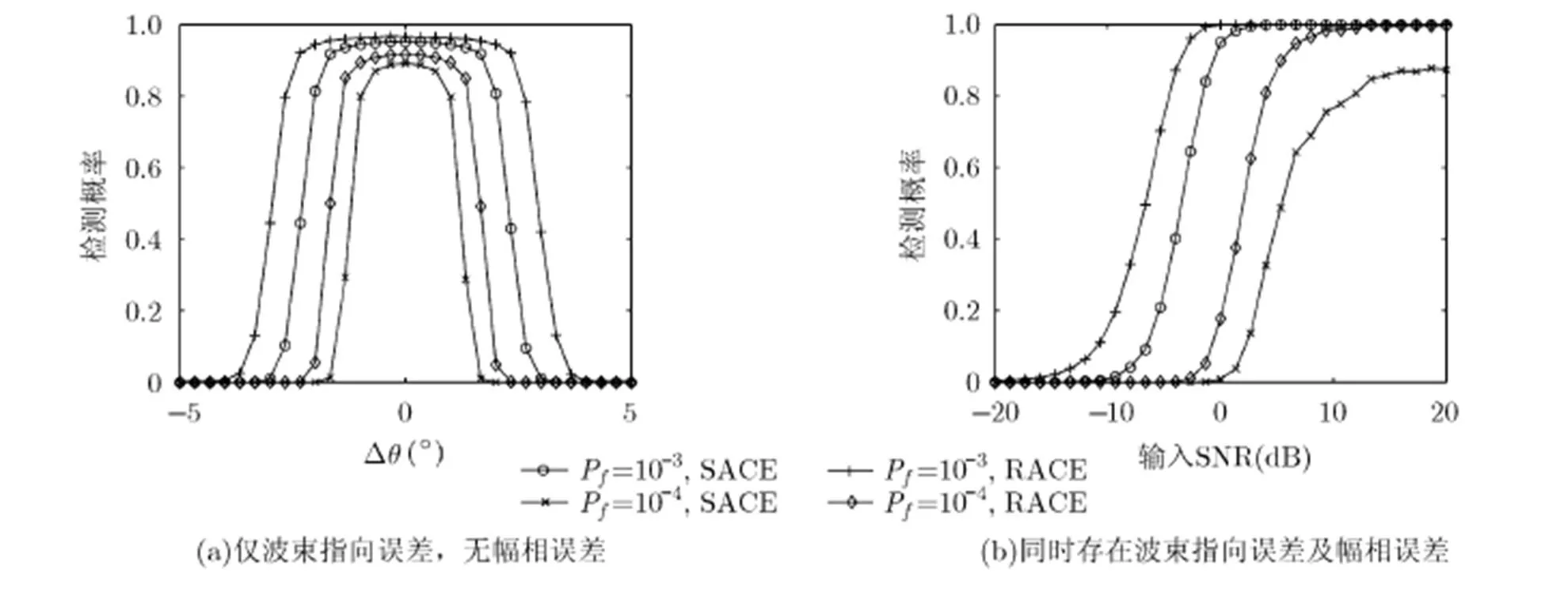
圖5 檢測概率隨輸入信噪比的變化情況
5 結束語
針對存在導向矢量誤差時ACE檢測器性能下降這一問題,在深入分析ACE檢測器的工作機理及其影響參數的基礎上,本文提出了一種基于橢球不確定集約束的魯棒ACE檢測器設計方法。利用導向矢量的尺度不影響輸出ACE檢測器輸出這一特性,將非凸的魯棒ACE檢測器設計問題轉化為凸優化問題,并給出了求解該問題的具體實施步驟。仿真結果表明,本文所給出的ACE檢測器具有較好的導向矢量誤差適應能力,能夠在有效抑制旁瓣目標的同時,降低檢測器對導向矢量誤差的敏感性。需要說明的是本文方法在給定橢球不確定集的情況下,可以設計出具有較強魯棒性的ACE檢測器,但如何根據實際導向矢量誤差情況構建適當的橢球不確定集這一問題并沒有涉及,還需進一步研究。
[1] Kraut S, Scharf L, and Butler R. The adaptive coherence estimator: a uniformly most-powerful-invariant adaptive detection statistic[J]., 2005, 53(2): 427-438.
[2] Bidon S, Besson O, and Tourneret J. The adaptive coherence estimator is the generalized likelihood ratio test for a class of heterogeneous environments[J]., 2008, 15: 281-284.
[3] Wang P, Sahinoglu Z, Pun M,.. Knowledge-aided adaptive coherence estimator in stochastic partially homogeneous environments[J]., 2011, 18(3): 193-196.
[4] Raghavan R. Maximal invariants and performance of some invariant hypothesis tests for an adaptive detection problem[J]., 2013, 61(14): 3607-3619.
[5] Liu Jun, Zhang Zi-jing, Shui Peng-lang,.. Exact performance analysis of an adaptive subspace detector[J]., 2012, 60(9): 4945-4950.
[6] Hossain M, Milford G, Reed M,.. Efficient robust broadband antenna array processor in the presence of look direction errors[J]., 2013, 61(2): 718-727.
[7] De Maio A, De Nicola S, Farina A,.. Adaptive detection of a signal with angle uncertainty[J].&, 2010, 4(4): 537-547.
[8] Zhang Wei, Wang Ju, and Wu Si-liang. Robust Capon beamforming against large DOA mismatch[J]., 2013, 93(4): 804-810.
[9] Liu Ai-fei, Liao Gui-sheng, Ma Lun,.. An array error estimation method for constellation SAR systems[J]., 2010, 7(4): 731-735.
[10] Jia Wei-min, Jin Wei, Zhou Shu-hua,.. Robust adaptive beamforming based on a new steering vector estimation algorithm[J]., 2013, 93(9): 2539-2542.
[11] Khabbazibasmenj A, Vorobyov S A, and Hassanien A. Robust adaptive beamforming based on steering vector estimation with as little as possible prior information[J]., 2012, 60(6): 2974-2987.
[12] 金偉, 賈維敏, 姚敏立. 迭代對角加載采樣矩陣求逆魯棒自適應波束形成[J]. 電子與信息學報, 2012, 34(5): 1120-1125.
Jin Wei, Jia Wei-min, and Yao Min-li. Iterative diagonally loaded sample matrix inverse robust adaptive beamforming[J].&, 2012, 34(5): 1120-1125.
[13] Li Jian, Stoica P, and Wang Zhi-song. Doubly constrained robust Capon beamformer[J]., 2004, 52(9): 2407-2423.
[14] Lorenz R and Boyd S. Robust minimum variance beamforming[J]., 2005, 53(5): 1684-1696.
[15] Jiang Xue, Zeng Wen-jun, Yasotharan A,.. Robust Beamforming by linear programming[J]., 2014, 62(7): 1834-1849.
[16] Press W, Teukolsky S, Vetterling W,.. Numerical Recipes in C: The Art of Scientific Computing[M]. 2nd Ed. New York: Cambridge University Press, 1992: 456-462.
代保全: 男,1985年生,博士生,研究方向為陣列信號處理、空時自適應信號處理.
王 彤: 男,1974年生,教授,研究方向為機載雷達運動目標檢測、合成孔徑雷達成像.
同亞龍: 男,1987年生,博士生,研究方向為陣列信號處理、空時自適應信號處理、雷達成像和動目標檢測.
吳建新: 男,1982年生,副教授,研究方向為空時自適應信號處理、雷達成像及動目標檢測.
保 錚: 男,1927年生,教授,研究方向為自適應信號處理、陣列信號處理、雷達成像和目標識別等.
Robust Adaptive Coherence Estimator Based on Ellipsoid Uncertainty Set Constraint
Dai Bao-quan Wang Tong Tong Ya-long Wu Jian-xin Bao Zheng
(,,710071,)
Adaptive Coherence Estimator (ACE) often suffers considerable performance degradation in the presence of steering vector errors. In this paper, a robust ACE detector based on the ellipsoid uncertainty set constraint is proposed. A detailed analysis of ACE detector is first conducted, which results in an interesting observation that scaling of the steering vector does not affect the statistical test of ACE. With this property exploited, a model for designing robust ACE detector is constructed and is subsequently converted into a convex optimization problem. Then, the solution to the problem is given with the powerful Newton-Raphson method. Simulation results show that the robustness of the proposed detector against the steering vector errors can be improved significantly compared with the standard ACE.
Radar signal processing; Adaptive coherence estimator; Steering vector errors; Ellipsoid uncertainty set; Robust detector
TN957.51
A
1009-5896(2014)12-2969-06
10.3724/SP.J.1146.2014.00563
王彤 twang@mail.xidian.edu.cn
2014-04-30收到,2014-07-03改回
國家自然科學基金(61372133, 61101241)和中央高校基本科研業務費專項資金(K50511020008)資助課題

