盾構機土壓平衡系統的ARMA模型及其參數估計

李守巨,霍軍周,曹麗娟

(1．大連理工大學工業裝備結構分析國家重點實驗室,遼寧大連 116023;2．大連理工大學機械工程學院,遼寧大連 116023;3．大連海洋大學機械與動力工程學院,遼寧大連 116023)

盾構機土壓平衡系統的ARMA模型及其參數估計

李守巨1,霍軍周2,曹麗娟3

(1．大連理工大學工業裝備結構分析國家重點實驗室,遼寧大連 116023;2．大連理工大學機械工程學院,遼寧大連 116023;3．大連海洋大學機械與動力工程學院,遼寧大連 116023)

為了表征盾構機土倉壓力平衡系統的時滯特性和提高模型的預測精度,建立了該系統的自回歸滑動平均(ARMA)模型,并提出了基于優化算法的ARMA模型參數估計方法。實驗結果表明,與經典的線性機理模型相對比,新模型顯著提高了土倉壓力的擬合和預測精度。ARMA模型預測土倉壓力的最大相對誤差從機理模型的41%降低到9%。結合實驗數據,分析了該系統動態響應的時滯特性,分析表明,螺旋輸送機轉速對下一時刻土倉壓力影響的時滯特性更加明顯。

自回歸滑動平均模型;參數估計;土壓平衡系統;盾構機;時滯特性

土壓平衡盾構機是地鐵隧道掘進過程中經常使用的機器類型之一,其土倉壓力的大小直接影響到掘進工作面的土壓力,決定了地表變形特征。因此,對盾構機土倉壓力平衡動態系統模型的研究引起了國內外的普遍關注。劉宣宇等提出了一種基于土倉壓力場梯度的土壓平衡盾構開挖面穩定性的判定方法,利用非均勻B樣條最小二乘方法建立了密封艙壓力場的分布模型[1];筆者基于改性后渣土的非線性本構關系,建立了盾構機土倉平衡系統的動態模型,提出了基于遺傳算法的土倉壓力系統模型參數辨識方法[2];Xu等在實驗室和現場研究了土壓平衡盾構機土倉壓力控制問題[3];Yang等建立了基于PID的土倉壓力控制模型,提出了盾構機推進系統的比例控制方法,并且在實驗臺驗證了控制算法的有效性[4];施虎等歸納了盾構設計和制造中所涉及到的6項關鍵技術,介紹盾構掘進模擬試驗方法及模擬試驗中的相似關系,重點論述體現盾構模擬試驗技術先進性的模擬試驗平臺的研制進展和現狀[5];王洪新采用流體力學理論推導了近似的土倉壓力及刀盤開口處壓力差計算方法,通過現場監測數據和離散元分析結果對公式進行了驗證和修正[6];施虎等采用自適應神經模糊推理系統(ANFIS)建立了一個以推進力、推進速度、土倉壓力實時數據采樣值為輸入,螺旋輸送機轉速為輸出的基于排土控制的盾構土壓平衡控制模型[7];夏毅敏等針對某地鐵施工工程需求,應用所開發的復合式土壓平衡盾構刀盤CAD系統進行了刀盤優化設計[8]。由于盾構機所穿越地層本身的復雜性和隨機性、土倉內渣土本構關系的非線性、土倉壓力變化對螺旋輸送機轉速改變響應的延遲性和渣土改性的不確定性,使得盾構機土倉壓力平衡系統具有時變性、時滯性、不確定性和非線性特性,很難從物理和力學、數學本質上得到精確的解析機理模型。盡管如此,機理模型卻能夠表征系統在線性、確定性和趨勢性上的輸入與輸出之間的內在映射關系。為了解決機理模型預測精度低、無法表征系統非線性和時變性問題,某些基于觀測數據的統計模型建模方法逐步為學術界所重視,其中有代表性的是自回歸滑動平均(ARMA)模型的統計建模方法。ARMA模型已經廣泛應用到模型辨識[9]、風速預測[10-11]、能力需求預測[12]、過程報警預測[13]、最優估計[14]、不確定性系統建模等領域[15],并且顯示了其優越性。但是,如何將ARMA建模方法應用到盾構機土壓平衡系統建模鮮見報道。本文基于盾構機土倉壓力平衡系統的線性機理模型,提出一種新的盾構機土壓平衡系統自回歸滑動平均模型,表征盾構機土倉壓力平衡系統的時滯特性,并實驗驗證新模型的有效性。

1 盾構機土壓平衡系統的自回歸滑動平均模型

盾構機土倉壓力受盾構機推進速度和螺旋輸送機的轉速影響,在大多數情況下,盾構機的推進速度設定為常數,通過實時調整螺旋輸送機的轉數控制土倉的壓力,進而控制掘進工作面的土壓力,最終實現控制地表變形的目的。當盾構機的推進速度為固定值時,盾構機土倉壓力與螺旋輸送機轉速之間的線性機理模型[2]為

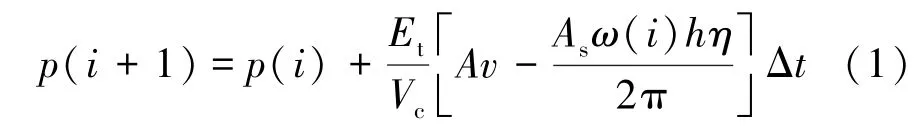
其中,p(i)和p(i+1)分別為當前時刻和下一時刻土倉壓力;Δt為采樣間隔時間;v為盾構機的推進速度; A為盾構機的橫截面積;h為螺旋輸送機的螺距;η為螺旋輸送機的排土效率;ω(i)為當前時刻的螺旋輸送機轉速;As為螺旋輸送機的有效排土面積;Vc為盾構機土倉體積;Et為渣土的等效變形模量。式(1)所建立的動態系統模型所存在的缺點在于沒有考慮到該系統的時滯特性,導致模型預測精度較低。

受式(1)的啟發,根據圖1所建立的盾構機土壓平衡系統的輸入與輸出關系,考慮到該系統的時滯特性,提出如下盾構機土倉壓力平衡系統的自回歸滑動平均(ARMA)模型:

其中,α,β,γ和λ為待估計模型中的系數;p(i-1)和ω(i-1)分別為前一時刻的土倉壓力和螺旋輸送機轉速。ARMA模型中的第1,2項為系統輸出(盾構機土倉壓力)的過去值的組合,即自回歸部分,反映土倉壓力過去值對當前值的影響;第3,4項為系統輸入(即螺旋輸送機的轉數)過去值的組合,即滑動平均部分,反映螺旋輸送機轉數過去值對土倉壓力當前值的影響。在盾構機土倉壓力平衡系統的ARMA模型參數確定之后,該模型就可以預測盾構機土倉壓力隨螺旋輸送機的變化規律,為盾構機土倉壓力控制提供系統模型。

圖1 盾構機土壓平衡系統的輸入與輸出Fig．1 Input and output of earth pressure balance system of shield

2 盾構機土壓平衡系統ARMA模型參數估計

在盾構機土倉壓力平衡系統的ARMA模型中,除了需要辨識確定的渣土的等效切線變形模量(Et)和螺旋輸送機的排土效率(η)之外,還包括系數α, β,γ和λ,而模型中的其他參數都是確定量。為了估計系統模型中的參數,定義如下的均方根誤差(root mean square error)為目標函數:

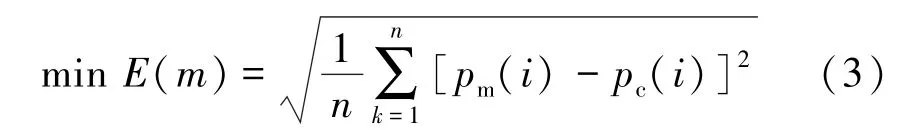
其中,pc(i)為按照式(2)由系統ARMA模型計算得到的土倉壓力,它是未知的模型參數矢量m={Et,η, α,β,γ,λ}T的函數,被辨識的模型參數包括渣土的等效變形模量Et和螺旋輸送機的排土率η以及系數α,β,γ和λ;pm(i)為實驗觀測到的土倉壓力;n為采樣數量。式(3)將系統辨識問題轉化為無約束優化問題,可以采用非線性最小二乘法、遺傳算法等優化方法求解。土壓平衡系統ARMA模型參數估計就是根據實驗觀測數據,在模型結構已知的條件下,采用基于優化搜索的系統辨識方法,通過不斷修正ARMA模型中的參數,使得ARMA模型的輸出(pc)與實驗觀測的土倉壓力(pm)之間的誤差達到最小值,如圖2所示。

圖2 ARMA模型參數估計Fig．2 Parameter estimation of ARMA model

為了獲得目標函數的極小值,估計ARMA模型中的參數,采用Gauss-Newton方法對參數估計問題進行求解。與擬牛頓算法相對比,Gauss-Newton方法不需要計算海森(Hessian)矩陣,而且收斂速度高于其他梯度搜索算法,其迭代格式為

其中,e為誤差矢量;J為ARMA模型計算的土倉壓力對模型參數的Jacobian矩陣;ρk為迭代步長;dk為Gauss-Newton方向矢量;k為迭代次數,而步長ρk可以通過二次插值方法或者試錯方法優化確定。Jacobian矩陣J中的元素由靈敏度系數表示

其中,Jij為第i時刻土倉壓力計算值對第j個模型參數mj的靈敏度;Δmj為第j個模型參數增量;Ij為第j個單位矢量。當不同時刻土倉壓力觀測值和螺旋輸送機的轉速已知,根據目標函數(3),采用Gauss-Newton優化搜索方法就可以估計出ARMA模型中的參數。

3 實驗研究

為了驗證所提出新模型的有效性,在大連理工大學盾構機試驗臺上進行了實驗研究。盾構機土倉壓力控制試驗臺由液壓油缸推進系統、刀盤旋轉驅動系統、螺旋輸送機排土系統、觀測數據采集系統和土倉壓力控制系統組成(圖3)。其中,推進系統的推進速度是參考盾構機實際掘進速度和試驗臺模型的比例確定的,并且由PLC程序控制。根據螺旋輸送機和盾構機試驗臺推進裝置的基本特性,確定采樣間隔時間為1 s,土倉壓力的初始壓力為56 kPa,刀盤的推進速度為v=20 mm/min,設計的螺旋輸送機轉速在0．2～1．2 rad/s變化,如圖4所示;觀測的土倉壓力在10～80 kPa變化,如圖5所示。螺旋輸送機的主要幾何特征尺寸為有效面積As為18 142．7 mm2,螺距h為128 mm,排土速率q為36．8×10-6mm3/s,平衡轉速為0．573 rad/s,推進速度為20 mm/min,螺旋輸送機排土率η=1．0。土倉的主要幾何特征尺寸直徑為 900 mm,寬度為 128 mm,橫截面積 A為0．636 m2,體積Vc為0．081 4 m3。土倉內渣土的改性材料包括膨潤土泥漿、泡沫和水,3種改性材料占原狀土體的比例分別為6%,20%和10%左右。

圖3 盾構機土倉壓力控制試驗臺Fig．3 Testing device for controlling earth pressure in chamber of shield

根據圖4螺旋輸送機轉速隨時間變化和圖5土倉壓力隨時間變化的實驗數據,以及新建的土倉壓力系統的ARMA模型,采用優化方法估計ARMA模型中的參數,表1給出了根據實驗數據得到的線性機理模型和ARMA模型的參數。在圖3,4中,前240組數據用來進行模型參數估計,后120組參數用來進行預測。

圖4 螺旋輸送機轉速隨時間的變化Fig．4 Variation of conveyor rotation speed versus time

圖5 土倉壓力隨時間的變化Fig．5 Variation of chamber pressure versus time

表1 系統模型參數辨識結果Table 1 Identified model parameters for different model

從表1可以看出,線性機理模型所得到的螺旋輸送機排土效率大于100%,很顯然是不盡合理的。模型參數α和γ表征了土倉壓力平衡系統的線性部分,該線性部分正是線性機理模型所表征的。模型參數β和λ表征了該系統的時滯部分,此部分恰恰是ARMA模型所特有的,參數β和λ的引入將會顯著提高模型的預測精度。從該4個參數的大小對比可以發現,螺旋輸送機的轉速對土倉壓力平衡系統影響的時滯特性更加明顯,進一步揭示了該系統時滯特性的物理本質。與盾構機的直徑相對比,螺旋輸送機直徑小一個數量級,改變螺旋輸送機的轉速并不能立即改變土倉壓力,而是需要又一個滯后過程,這也就是ARMA模型能夠比較準確表征土倉壓力平衡系統特性的原因所在。

如圖6所示,機理模型擬合最大相對誤差48%,預測最大相對誤差41%。ARMA模型擬合最大相對誤差14%,預測最大相對誤差9%,新模型明顯提高了擬合和預測精度。

圖6 土倉壓力預測值與觀測值的對比Fig．6 Comparison between forecast pressure and observed pressure

4 結 論

(1)土壓平衡盾構機土倉壓力平衡系統的工作性態表現出較強的時滯特征,簡單的線性模型無法精確表征該動力系統的時滯特性,ARMA模型為解決這一課題提供了新的途徑。

(2)實驗結果表明,線性機理模型擬合的最大相對誤差為48%,預測最大的相對誤差為41%。ARMA模型擬合最大相對誤差為14%,預測最大相對誤差為9%。與經典的線性機理模型相對比,ARMA模型的擬合精度和預測精度得到了顯著的提高,盾構機土倉壓力平衡系統的ARMA模型精確地表征了該系統的時滯特性。

(3)模型參數α和γ表征了土倉壓力平衡系統的線性部分,該線性部分正是線性機理模型所表征的。模型參數β和λ表征了該系統的時滯部分,此部分恰恰是ARMA模型所特有的,參數β和λ的引入將會顯著提高模型的預測精度。與盾構機的直徑相對比,螺旋輸送機直徑小一個數量級,改變螺旋輸送機的轉速并不能立即改變土倉壓力,而是需要又一個滯后過程,這也就是ARMA模型能夠比較準確表征土倉壓力平衡系統特性的本質所在。

(4)盡管ARMA模型給出了較高的土倉壓力擬合和預測精度,但是該模型并沒有考慮到該系統的時變性、非線性和隨機性。渣土的等效變形模量和螺旋輸送機的排土效率可能是土倉壓力的函數,同時盾構機掘進過程中地質條件隨機變化,如何考慮這些復雜因素的影響進行土壓平衡系統建模是本課題進一步深入研究的內容。

[1] 劉宣宇,邵 誠,劉東昭．基于密封艙壓力場梯度的盾構開挖面穩定性判定[J]．煤炭學報,2012,37(10):1463-1468．

Liu Xuanyu,Shao Cheng,Liu Dongzhao．Stability judgment of shieldexcavation face based on earth pressure field gradient in pressure chamber[J]．Journal of China Coal Society,2012,37(10):1463-1468．

[2] 李守巨,曹麗娟．盾構機土倉壓力控制模型及其參數辨識[J]．煤炭學報,2012,37(2):206-210．

Li Shouju,Cao Lijuan．Pressure control model on soil chamber of shield machine and its parameter identification[J]．Journal of China Coal Society,2012,37(2):206-210．

[3] Xu Qianwei,Zhu Hehua,Ding Wenqi．Laboratory model tests and field investigations of EPB shield machine tunneling in soft ground in Shanghai[J]．Tunneling and Underground Space Technology, 2011,26(1):1-14．

[4] Yang Huayong,Shi Hu,Gong Guofang,et al．Electro-hydraulic proportional control of thrust system for shield tunneling machine[J]．Automation in Construction,2009,18(7):950-956．

[5] 施 虎,楊華勇,龔國芳．盾構掘進機關鍵技術及模擬試驗臺現狀與展望[J]．浙江大學學報(工學版),2013,47(5):741-749．

Shi Hu,Yang Huayong,Gong Guofang．Key technologies of shield tunneling machine and present status and prospect of test rigs for tunneling simulation[J]．Journal of Zhejiang University(Engineering Science),2013,47(5):741-749．

[6] 王洪新．土壓平衡盾構刀盤開口率對土艙壓力的影響[J]．地下空間與工程學報,2012,8(1):89-93．

Wang Hongxin．Influence of aperture ratio of cutterhead of EPB shield on earth pressure in the chamber[J]．Chinese Journal of Underground Space and Engineering,2012,8(1):89-93．

[7] 施 虎,龔國芳,楊華勇．盾構掘進土壓平衡控制模型[J]．煤炭學報,2008,33(3):343-346．

Shi Hu,Gong Guofang,Yang Huayong．Control model of earth pressure balance for shield tunneling[J]．Journal of China Coal Society, 2008,33(3):343-346．

[8] 夏毅敏,卞章括,暨智勇,等．復合式土壓平衡盾構刀盤CAD系統開發[J]．計算機工程與應用,2012,48(36):64-69．

Xia Yimin,Bian Zhangkuo,Ji Zhiyong,et al．Development of cutter head CAD system for composite EPB shield[J]．Computer Engineering and Applications,2012,48(36):64-69．

[9] Yao Guoyu,Ding Ruifeng．Two-stage least squares based iterative identification algorithm for controlled autoregressive moving average (CARMA)systems[M]．Computers and Mathematics with Applications,2012,63:975-984．

[10] Erasmo Cadenas,Wilfrido Rivera．Wind speed forecasting in three different regions of Mexico,using a hybrid ARIMA-ANN model [J]．Renewable Energy,2010,35:2732-2738．

[11] Ma Lei,Luan Shiyan,Jiang Chuanwen．A review on the forecasting of wind speed and generated power[J]．Renewable and Sustainable Energy Reviews,2009,13:915-920．

[12] Volkan S,Edigera,Sertac Akar．ARIMA forecasting of primary energy demand by fuel in Turkey[J]．Energy Policy,2007,35:1701-1708．

[13] 王 鋒,李宏光,臧 灝．基于Logistic和ARMA模型的過程報警預測[J]．化工學報,2012,63(9):2941-2947．

Wang Feng,Li Hongguang,Zang Hao．Process alarm prognosis based on Logistic and ARMA models[J]．CIESC Journal,2012,63 (9):2941-2947．

[14] 孫書利,劉麗芳．具有隨機多丟包的ARMA信號最優線性估計[J]．控制與決策,2013,28(2):223-228．

Sun Shuli,Liu Lifang．Optimal linear estimation for ARMA signals with stochastic multiple packet dropouts[J]．Control and Decision, 2013,28(2):223-228．

[15] 王紅瑞,高 雄,錢龍霞．基于ARMA-GARCH模型的水文過程不確定性分析[J]．中國科學:技術科學,2012,42(9):1069-1080．

Wang Hongrui,Gao Xiong,Qian Longxia．Uncertainty analysis of hydrological processes based on ARMA-GARCH model[J]．Scientia Slnica Technologica,2012,42(9):1069-1080．

Autoregressive moving average model and its parameter estimation for earth pressure balance system of shield

LI Shou-ju1,HUO Jun-zhou2,CAO Li-juan3
(1.State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian University of Technology,Dalian 116023,China 2.School of Mechanical Engineering,Dalian University of Technology,Dalian 116023,China 3.School of Mechanical and Power Engineering,Dalian Ocean University,Dalian 116023,China)

In order to characterize time delaying property and increase forecasting precision of earth pressure balance system of shield,an autoregressive moving average(ARMA)model was proposed．Based on optimization algorithm,parameter estimation procedure was presented to determine ARMA model parameters．The experimental investigation shows that compared with classic mechanism model,ARMA model obviously increases fitting and forecasting precisions．The maximum relative error of computed earth pressure falls from 41%to 9%forecasted by ARMA model．According to experimental data,the time delaying properties of the dynamic response of the system was discussed．The affection of past rotating speed of conveyor on earth pressure on next time is more obvious．

autoregressive moving average model;parameter estimation;earth pressure balance system;shield;time delaying property

TD263

A

0253-9993(2014)11-2201-05

2013-10-10 責任編輯:常 琛

國家重點基礎研究發展計劃(973)資助項目(2013CB035402);國家自然科學基金重點資助項目(51105048);工業裝備結構分析國家重點實驗室開放基金資助項目(S14206)

李守巨(1960—),男,遼寧沈陽人,教授,博士。E-mail:lishouju@dlut．edu．cn

李守巨,霍軍周,曹麗娟．盾構機土壓平衡系統的ARMA模型及其參數估計[J]．煤炭學報,2014,39(11):2201-2205．

10．13225/j．cnki．jccs．2013．1470

Li Shouju,Huo Junzhou,Cao Lijuan．Autoregressive moving average model and its parameter estimation for earth pressure balance system of shield[J]．Journal of China Coal Society,2014,39(11):2201-2205．doi:10．13225/j．cnki．jccs．2013．1470