單輪自平衡機器車的系統建模與最優控制

張團善，李文真

(西安工程大學電子信息學院，陜西西安710048)

單輪自平衡機器車的系統建模與最優控制

張團善，李文真

(西安工程大學電子信息學院，陜西西安710048)

針對高階次、多變量、非線性、欠驅動的單輪自平衡車系統，提出了一種改進的最優控制算法.首先采用拉格朗日方程推導出力學模型，線性化后，得到系統的線性化方程，然后分別利用線性二次型最優控制算法和基于對稱根軌跡的最優控制算法實現了單輪機器車的平衡控制和動態穩定.通過比較可以看出，基于對稱根軌跡的最優控制算法較傳統的最優控制算法有更好的穩定性和魯棒性，仿真結果驗證了力學模型的正確性和反饋線性化控制算法的有效性.

單輪自平衡機器車;拉格朗日方程;線性二次型;對稱根軌跡

0 引言

單輪自平衡機器車作為一種新型的環保輕型代步工具以其體積小、功耗低、易于控制、適應地形變化能力強等特點，引起了許多業內研究者的興趣.與其他類型的機器車相比，自平衡機器車最主要的特征是要在各種狀態下保持機器車的姿態平衡［1］.單輪自平衡機器車的工作原理是通過收集外部采集的數據，設計平衡控制算法和反饋調節器使系統達到動態平衡.Salerno等人根據倒立擺特性，以機器車車體的旋轉角度為變量得到了雙輪自平衡機器車的動力學方程，并通過應用微分幾何方法對系統各種控制器參數的狀態變量進行了分析［2］;Vos等人針對典型的倒立擺自平衡機器車系統提出了一種自適應控制算法，實現了機器車的平衡控制，但沒有實現其運動控制［3］;美國加州大學的學生研制出了一款帶豎直飛輪和行走輪的自平衡機器車，利用極點配置算法實現了自身的平衡［4］;郭磊等人研究了一種帶水平飛輪和運動配重機構的自平衡機器車，并根據線性理論MIMO方法設計了控制算法并進行了測試［5］.由于上述研究中的自平衡機器車結構復雜、非線性程度高，其良好的控制效果是建立在精確數學模型的基礎上，用簡單的PID調節器和狀態反饋控制器難以實現機器車的動態平衡，需要設計復雜的非線性控制器，成本較高，故本文對只保留行走輪的單輪機器車進行了數學建模并使用傳統的線性二次型最優控制算法和基于對稱根軌跡的最優控制算法分別進行控制，實現了機器車的動態鎮定和自平衡，同時兼顧了系統響應的快速性和穩定性.這樣的設計簡化了機器車的結構，增加了實用性，降低了控制難度并提高了線性控制算法的可靠性.仿真結果表明，在一定角度范圍內，兩種控制算法均能使系統達到穩定平衡狀態，而SRL最優控制算法比傳統的最優控制算法更有利于提高機器車的動態性能.

1 結構和動力學模型

1.1 結構特點及運動原理

單輪自平衡機器車的機械結構由車輪本體，內嵌的伺服電機和輪軸外側的踏板組成;控制系統主要包括驅動器、傳感器和控制板，如圖1所示.

單輪自平衡機器車是個結構不穩定的系統，具有靜不平衡性，必須采用動態平衡的策略，即讓機器車在平衡點附近不停地運動進行調節.如果將人等效為直立的車體，則對單輪機器車的運動控制最終表現為對車輪位移和車體傾角的控制，即通過檢測裝置將傾角和位置信息反饋給執行電機，產生作用轉矩，對系統的狀態進行實時的反饋調節，使機器車按照給定的速度運動，同時保證車體的轉角為零.

1.2 模型建立及參數說明

將直立的人等效為直立的車體，當人站立在輪軸兩側的踏板上時，整個系統的重心位于輪子上方，而車輪只有一個支點與地面接觸，如圖2所示.建立模型前，假設以下條件：(1)車輪、車體均為剛體;(2)不考慮機器車和車體所受的外界干擾力;(3)不考慮車體與輪子之間的滑動摩擦力; (4)車輪與地面不打滑.建立如圖3所示直角坐標系，規定機器車的前進方向為x軸正方向，與y軸垂直，輪子的軸線方向為z軸方向.

設車輪質量為m，車體質量為M，車輪半徑為R，輪心到車體質心的距離為L，車輪繞z軸的轉角為θR，車體繞y軸的轉角為θP，電機對車輪的轉矩為C，車輪的位移為xR，車體對Y軸的轉動慣量為Jpθ，車輪對Z軸的轉動慣量為JR.

圖1 單輪自平衡機器車實物照片

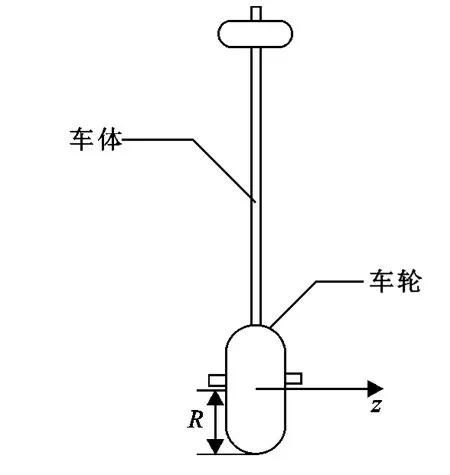
圖2 單輪機器車結構圖

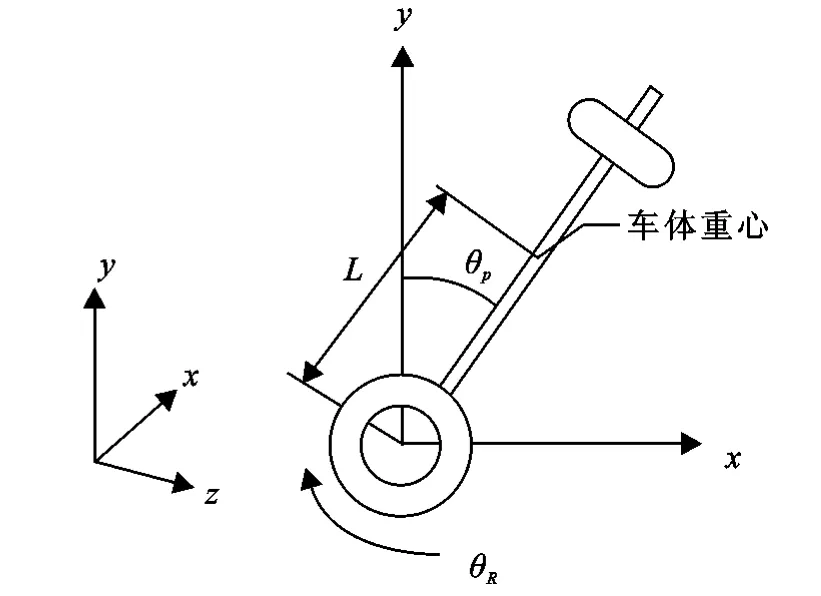
圖3 系統坐標系和幾何參數含義

自平衡機器車有車輪位移、車體轉角兩個自由度，但只有一個控制輸入(電機的作用轉矩)，是典型的欠驅動系統.嚴格地講，它和倒立擺一樣，是一種欠驅動連桿系統，其中車輪是主動關節，車體屬于被動執行機構，車輪位移與車體轉角兩變量之間存在耦合關系［6］.由于欠驅動連桿系統具有多變量、強耦合的特性，用牛頓力學的分析方法為其建立準確的數學模型將十分復雜，因此本文選用拉格朗日方程從能量學的角度對系統進行動力學建模.其中數學表達式為

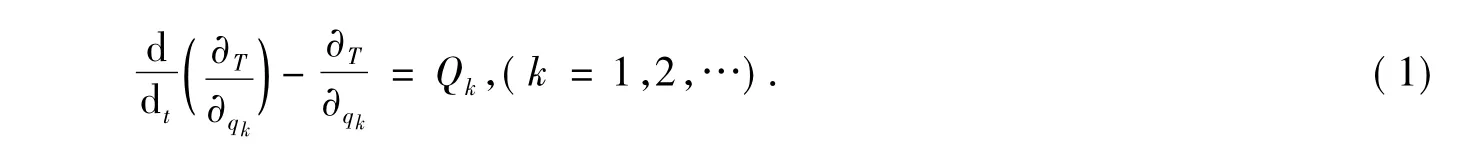
式中T為系統的總動能，q為系統的廣義坐標，Q為系統的廣義力.

選取車輪轉角和車體轉角作為系統的運動狀態變量，由這兩個相互獨立的狀態變量可以惟一確定系統的位置，在此坐標系下，車輪轉角對應的廣義力等于電機對車輪的作用轉矩，而車體轉角對應的廣義力等于車體重力與電機對車體的作用轉矩，即

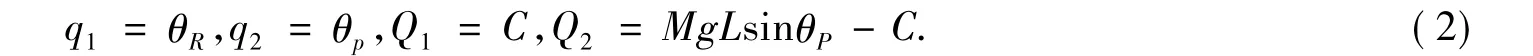
系統的動能包括車輪的平動動能T1，車輪繞z軸的轉動動能T2，車體的平動動能T3，車體繞過其質心且平行于z軸的轉動動能T4，表達式如下

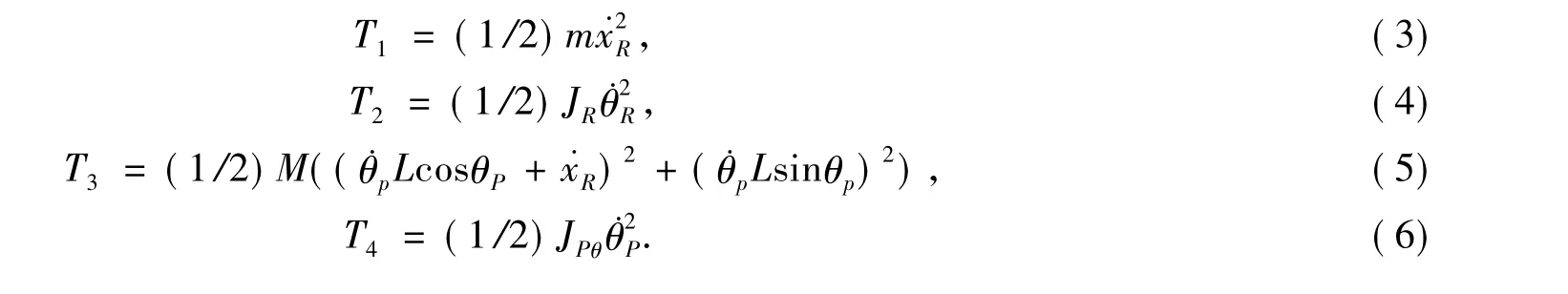
系統總動能為

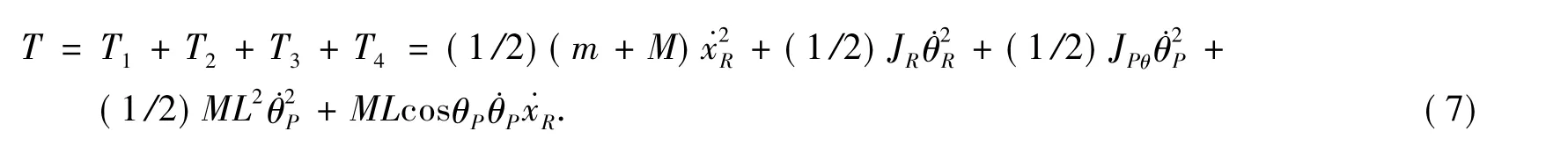
為簡化模型和局部線性化，對車體的轉角做如下約束：在平衡點附近時令sinθp≈θp，cosθp≈1.將式(2)～(7)代入式(1)，可得以下線性方程組：

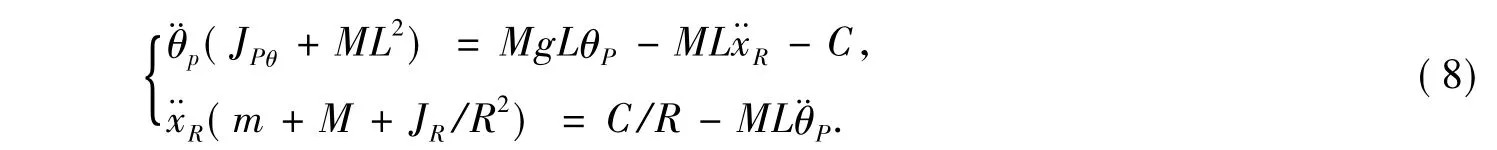
整理式(8)，并代入系統參數可得到線性化的數學模型：

系統參數見表1(注：為了方便后期系統模型的制作與硬件調試，在建立參考模型時對整個系統進行了適當的縮小).

表1 系統參數

由系統的狀態方程知，該系統是單輸入多輸出的欠驅動系統，但各個狀態變量之間存在耦合，結合能量傳遞的思想，對不可驅動狀態變量的控制可以通過對可驅動狀態變量的控制來間接達到.因此，可以通過狀態反饋實現對整個欠驅動系統的實時控制.

用拉格朗日方程建立模型的方法是從總體能量的角度考慮，故在模型建立的過程中可以忽略系統內部之間的作用力，通過選擇不同的狀態量和輸出量達到不同的控制效果［7］，為了達到全面的控制效果，將系統的4個狀態量均選為輸出量，對系統實施全反饋控制.

結合能控性判別矩陣M=［B，AB，A2B，A3B］，經MATLAB計算得rank(M)=4，系統能控;同理，由系統能觀性矩陣N=［C，CA，CA2，CA3］T可知，rank(N)=4，系統能觀.

1.3 系統的穩定性分析

線性定常系統穩定的充要條件是其全部特征根均具有負實部［8］.因本文將單輪自平衡機器車近似為不隨時間改變的線性系統，故可以通過線性定常系統的穩定性判據對系統進行判穩.

由特征值方程

可得系統的特征值為

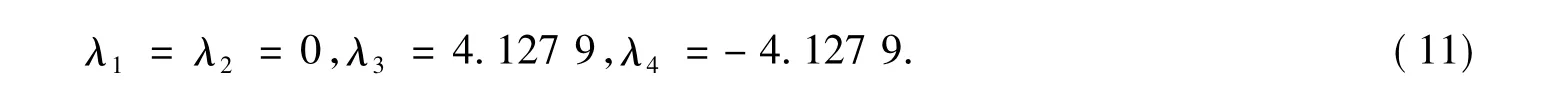
從式(11)可以看出，系統有一個正特征值和兩個零特征值，不滿足勞斯穩定的必要條件，而且無論怎樣調節系統的參數，都無法使之達到穩定的狀態.反饋控制可以將閉環系統的極點配置在根平面上所期望的位置，使系統達到穩定狀態，而任意配置極點的充要條件是系統能控能觀［9］，這是上文判斷能控能觀性的意義所在.

圖4是系統的開環階躍響應，可以看出此時系統是不穩定的，這與上述穩定性分析的結果一致.

圖44 個狀態量的開環階躍響應

2 系統控制器設計

2.1 LQR控制器設計

單輪機器車的平衡問題，是一個狀態正定問題，目標是在行走時使車體保持直立的狀態，由于單輪自平衡機器車是一個高階系統，使用傳統的PI調節器進行控制時位移和速度曲線的振蕩較為嚴重，甚至出現系統失控的現象［10］.因此本文選擇了線性最優控制理論來設計反饋控制算法，目標是在車體的傾角為零，位移和速度穩定在固定值的基礎上，使系統的性能指標達到極小.根據無限時間的線性二次型最優狀態調節器理論，當tf趨于無窮時，最優控制問題等效為尋找一個控制量u(t)=-kx(t)使得以下的二次型性能指標［11］達到極小值：

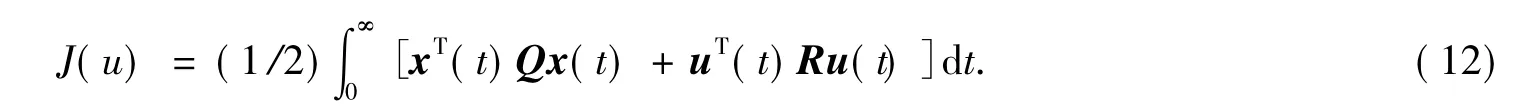
式中x(t)為n維狀態向量;u(t)為r維控制向量;Q矩陣是半正定m×m實對稱矩陣;R是正定r×r實對稱矩陣.

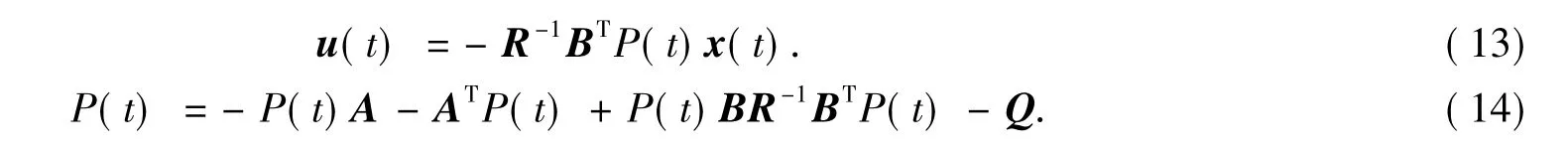
其中P(t)可由方程(14)解出;u(t)為主動控制力方程.

求解式(14)需要給定兩個重要參數，即Q矩陣和R矩陣.其中，Q矩陣代表狀態向量的權重，R矩陣則代表控制量的權重，它們分別表示系統運動過程中動態跟蹤誤差的總度量和能量消耗的總度量.在平衡控制中穩定的動態性能是首要要求，低能耗是次要要求，故取R=1.Q矩陣中的非零元素代表在控制過程中系統對各個狀態的誤差要求，經反復測試，并參照控制中車體和輪子的位移大小，取Q=［1000 0 0 0;0 0 0 0;0 0 100 0;0 0 0 0］.

因為Riccati方程較為復雜難解，在得知Q、R矩陣的前提下可以利用MATLAB函數庫中的lqr函數幫助求解式(13)和式(14)，得到系統的最優反饋增益矩陣

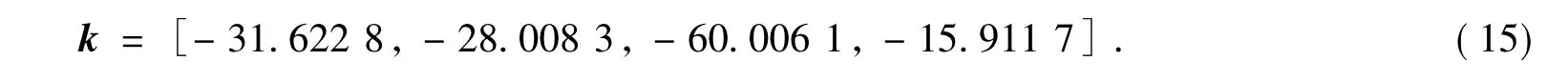
LQR控制方法的simulink仿真模型如圖5所示.經MATLAB仿真可得，在此控制方案下，系統4個狀態量的階躍響應如圖6所示.由圖6可以看出，給系統加入階躍擾動時，系統能夠較快地達到平衡狀態，在此過程中位移的超調量約為30mm，傾角的超調量約為0.02rad，調節時間約為2s，穩態誤差、上升時間也符合穩態要求.在此基礎上，如果再增加Q矩陣中的某些元素，系統的動態性能響應還會有所改善，但控制量也會上升，在保證控制量足夠小，兼顧其他動態響應指標的基礎上，此時的系統性能已經能夠滿足要求.

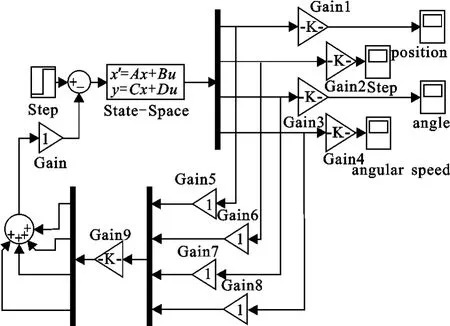
圖5 LQR仿真模型

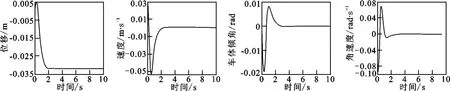
圖6 LQR控制下的系統仿真曲線

2.2 基于SRL的最優控制器設計

針對高階次的系統，采用極點配置實現狀態反饋的方法雖簡單直觀，但對期望極點位置的選擇十分復雜，且無法確定期望極點的最優或較優，傳統的LQR調節器雖通過確定加權矩陣的方法找到了最優的反饋增益矩陣，但確定加權矩陣Q和R的普遍方法是仿真試湊法，即先初步選取Q和R，如果符合要求就求出最優增益矩陣K.進行仿真實驗，如果不符合須重新選取，直至符合系統的性能指標要求［12］，矩陣中因數的選擇主要依賴于設計者的經驗和調試，具有較大的盲目性.因此，本文根據對稱根軌跡(SRL)的原理，把最優控制和極點配置的思想結合起來，選擇了一個新的性能指標函數，用于得到期望的最優閉環極點，即，將傳統的最優控制規律簡化描述成如下的性能指標［13］

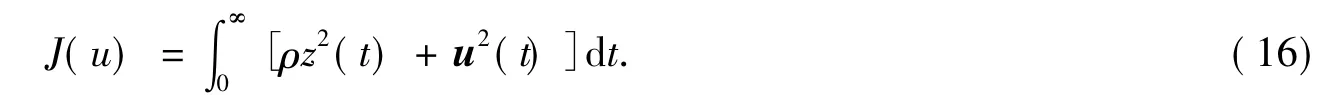
對如下的系統能夠最小，即

其中式(16)中的z2(t)為系統跟蹤誤差的權值，u2(t)為系統控制量的權值，ρ是加權系數又稱根軌跡參數，用于權衡跟蹤誤差對于控制量的相對損耗.以下是對稱根軌跡方程的解：

使J(u)最小化的控制規律由線性反饋u=-kx得到，這里k的最優值即以上對稱根軌跡方程中穩定根位置上的k值.可以看出s和-s對式(18)的影響是相同的，對于式(18)的任意根s0，必將對應一個根-s0，因此稱所得的根軌跡為對稱根軌跡，對稱的含義是此根軌跡關于原點對稱.最優主導極點可以由SRL中參數ρ所對應的穩定極點得到，在此根軌跡下選取的穩定極點具有使性能指標式(16)極小的特點，文獻［13-14］給出了SRL的產生過程和SRL上的穩定極點使性能指標式(16)極小的證明，在此不做闡述.

利用SRL設計最優控制器的過程是先選定矩陣H(H決定了系統的跟蹤誤差，需保持一個很小的值)，再根據式(18)畫出SRL曲線，在曲線中選取適當的ρ值(它平衡了跟蹤誤差和控制量對系統的重要性)，并找出與之對應的極點，然后將這些極點用于極點配置的運算中，得到反饋增益K，對系統進行反饋控制.

在上述理論基礎上結合系統對位置和角度的輸入要求，取跟蹤誤差矩陣H為

代入式(17)可得系統跟蹤輸出與控制輸入的傳遞函數

圖7給出了由式(18)所得的對稱根軌跡.

由于最優的閉環極點一定是穩定的，所以選擇左半S平面上的極點.經MATLAB計算得：當ρ=1時，對應的極點為-4.14+0.24i，-4.14-0.24i，選擇這兩個極點作為主導極點，在此基礎上，取-20+i和-20-i作為輔助極點，它們位于主導極點的左側，距離虛軸的距離是主導極點的5倍，對系統的影響較小.故期望的閉環極點為［-20+i，-20-i，-4.14+0.24i，-4.14-0.24i］.

結合MATLAB的狀態反饋函數：K=acker(A，B，P)得出反饋增益矩陣，其中，P為各個期望極點的值，即

將新的最優反饋矩陣K代入圖5的Simulink仿真模型中，可以得出在此控制方案下，4個狀態量的階躍響應，SRL控制下的系統仿真曲線如圖8所示.

由圖8可以看出，改進后系統的調節時間大約是0.5s，比傳統的LQR控制器的調節時間縮短了1.5s，響應速度變快，超調量也明顯減小，動態穩定性有所提高.結果表明，參數ρ的選擇是合理的.

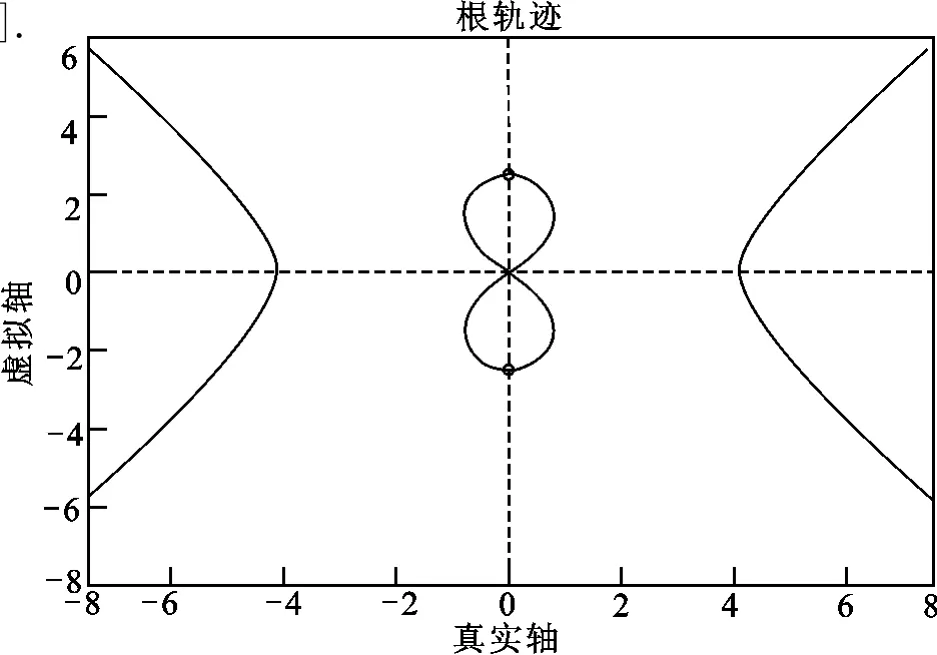
圖7 機器車系統的對稱根軌跡

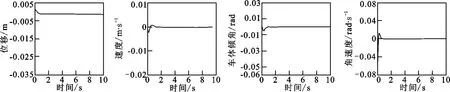
圖8 SRL控制下的系統仿真曲線

在選擇期望極點時，應該考慮系統的動態性能和閉環極點對于控制量的影響，否則容易導致控制量過高.傳統的最優控制算法雖使控制量達到了一個較小的值，卻無法建立起性能指標與系統誤差之間的聯系，并且確定權矩陣是很困難的，必須經過多次實驗找到合適的加權矩陣.而基于參數的SRL最優控制方法在一定程度上抑制了選擇加權矩陣時對系統的主觀影響，使控制方法更易把握，并用參數ρ平衡了輸入量與跟蹤誤差對系統的影響，實現了最優和穩定的統一.

參數ρ的選取有一定的限制條件.當ρ→0時，被控對象處于“高代價控制”情況，不利于控制能量的利用，很低的控制使用在系統的跟蹤輸出量z上產生了很大的誤差;而當ρ→∞時，被控對象處于“廉價控制”的情況，在這種情況下，反饋增益矩陣K是無界的，同樣不利于實際系統的控制.因此，本文在選取參數ρ時全面考慮了系統根的位置、時間響應、反饋增益、阻尼比等因素，并進行了大量的實驗，最終達到了控制量、跟蹤誤差與控制效果之間的動態平衡.

綜上所述，SRL法既得到了理想的最優閉環極點進而保證了良好的控制性能，又能在系統誤差與控制量之間達到動態平衡，綜合了最優控制理論和反饋控制方案，達到了控制量與控制效果的統一.較之傳統的LQR控制，對稱根軌跡法控制的超調量小、控制方法簡單、響應速度快，在實際中具有更高的應用價值.

3 結束語

單輪自平衡機器車是非線性、欠驅動、高階次系統的典型代表之一，本文在局部線性化的基礎上用全狀態反饋實現了對欠驅動狀態變量的間接控制，并采取構造不同的線性二次型最優性能指標函數的方法，設計了平衡控制算法.仿真結果表明，基于LQR的最優控制方法和基于SRL的最優控制方法都可以使單輪自平衡機器車系統達到穩定狀態，而基于SRL的最優控制方法既消除了LQR控制算法中選取Q，R矩陣的不確定性，又利用參數ρ的選擇，找出了系統響應與期望極點的位置、時間響應及反饋增益之間的關系，控制方法簡單、響應速度快、超調量小，因此在實際中具有更高的應用價值.

［1］阮曉剛.兩輪自平衡機器人的研究與設計［M］.北京：科學出版社，2012：10-17.

［2］A SALERNOA，J Nonlinear.On the nonlinear controllability of a quasiholonomic mobile robot［C］//Proc of IEEE ICRA，Taiwan，2003：3379-3384.

［3］VOS D W，Von FLOTOW A H.Dynamics and nonlinear adaptive control of an autonomous unicycle：Theory and experiment［C］.IEEE，USA：1990：182-187.

［4］常文超.自平衡獨輪機器人控制系統的研究［D］.河北：河北科技大學，2012.

［5］郭磊.單輪車機器人的動力學建模與非線性控制［J］.系統仿真學報，2009，21(9)：2730-2733.

［6］孫寧.一類欠驅動系統的控制方法綜述［J］.智能系統學報，2011，6(3)：200-203.

［7］阮曉剛.兩輪自平衡機器人動力學建模及其平衡控制［J］.計算機應用研究，2009，26(1)：99-103.

［8］劉豹.現代控制理論［M］.北京：機械工業出版社，2001：157-177.

［9］鄭大鐘.線性系統理論［M］.北京：清華大學出版社，2002：281-283.

［10］FAIZAN F，FARID F，REHAN M.Implementation of discrete PID on inverted pendulum［J］.Education Technology and Computer，2010，70(11)：48-51.

［11］吳受章.應用最優控制［M］.西安：西安交通大學出版社，1987：10-20.

［12］POWELL J David.動態系統的反饋控制［M］.朱齊丹，譯.北京：電子工業出版社，2004：138-190.

［13］T Kailath.Linear systems［M］.Englewood Cliffs：Prentice Hall，1980：158-258.

［14］ROB Hoogendijk，A J Den Hamer，GEORGO Angelis，et al.Frequency response data based optimal control using the data based symmetric root Locus［C］//2010 IEEE International Conference on Control Applications，Yokohama，Japan，2010： 1010-1015.

System modeling and optimal control for the self-balancing unicycle

ZHANG Tuan-shan，LI Wen-zhen

(School of Electronics and Information，Xi'an Polytechnic University，Xi'an 710048，China)

An improved optimal approach is proposed for the high order，multivariate，typical nonlinear underactuated unicycle.The dynamical model is firstly established based on Lagrangian formulation.The tangent linearization of the model at its equilibrium yields to the linearization nominal model.Then respectively using LQR optimal algorithm and SRL optimal control algorithm to achieve dynamic balancing and motion control of the unicycle.By the simulation comparisons，SRL optimal control algorithm has a better anti-jamming and robustness than LQR optimal control algorithm.Computer simulation verifies the validity of the dynamic model，the effect of the controller is testified by simulation experiments.

self-balancing unicycle;Lagrangian equations;linear quadratic regulator(LQR);symmetrical root locus(SRL)

TP 242

A

1674-649X(2014)01-0077-07

Lagrange乘子進行求解，可以得到

編輯：武暉;校對：孟超

2013-08-04

張團善(1971-)，男，湖北省隨州市人，西安工程大學副教授，碩士生導師.E-mail：zz102@sina.com