基于包含度理論的概念格構造方法研究

何 苗，石 慧，魏 玲

(西北大學數學系，陜西西安 710127)

Wille R.于1982年首先提出了形式概念分析理論[1－2]，用于概念的發現、排序和顯示。形式背景與形式概念是形式概念分析的基本概念，形式概念是由形式背景中的對象集和屬性集組成的統一體，形式概念之間可形成一種有序的層次結構——概念格，概念格的構造[3－5]是形式概念分析理論的主要研究內容之一。

Duntsch和Gediga把粗糙集中的上、下近似算子引入概念格理論中，得到了面向屬性概念格[6]。類似地，Yao獲得了面向對象概念格，并對兩者之間的關系做了進一步的研究[7－9]。包含度理論[10]是張文修教授提出的一種定量化不確定性的理論，是對“包含關系”的擴充，從而包含了“關系”的不確定性。作者利用包含度基于形式背景定義了4種新的算子，并證明了當包含度取不同的值時，可以構造4種概念格，即經典概念格、補背景概念格、面向屬性概念格和面向對象概念格。因而，本文提出的基于包含度理論構造概念格的方法可以實現對多種概念格構造方法的統一。

1 預備知識

定義1[2]稱(G，M，I)為一個形式背景，其中G={g1，…，gt}為對象集，每個gi(i≤t)稱為一個對象;M={m1，…，ms}為屬性集，每個mj(j≤s)稱為一個屬性;I為G和M之間的二元關系I?G×M。若(g，m)∈I，則稱g具有屬性m，用gIm表示。

對于形式背景(G，M，I)，在對象集X?G和屬性集B?M上分別定義運算

X*={m|m∈M，?g∈X，gIm}，

B'={g|g∈G，?m∈B，gIm}。

?g∈G，記{g}*為g*;?m∈M，記{m}'為m'。若?g∈G，g*≠?，g*≠G，且?m∈M，m'≠?，m'≠M，則稱形式背景(G，M，I)是正則的。本文提到的形式背景都是正則的。

對于二元關系I，定義其補關系Ic={(g，m)|? (gIm)}，則形式背景(G，M，Ic)是(G，M，I)的補形式背景。

設(G，M，I)是形式背景，?A?G，B?M，若滿足A*=B且A=B'，則稱(A，B)是一個形式概念，簡稱概念;其中A稱為概念的外延，B稱為概念的內涵。形式背景(G，M，I)的全體概念記為 L(G，M，I)。?(A1，B1)，(A2，B2)∈ L(G，M，I)，定義

(A1，B1)∧ (A2，B2)=(A1∩ A2，(B1∪B2)'*)，

(A1，B1)∨ (A2，B2)=((A1∪ A2)*'，B1∩B2)，

則L(G，M，I)是完備格，稱為概念格。

定義2[6]設(G，M，I)是形式背景，?X?G，B?M，定義一對近似算子◇，□，:

X◇={m|m∈M，m'∩X≠?}，

B□={g|g∈G，g*?B}。

定義3[6]設(G，M，I)是形式背景，?X?G，B?M，若一個二元組(X，B)滿足X◇=B，B□=X，稱(X，B)為面向屬性概念。

記 LP(G，M，I)={(X，B)|X◇=B，B□=X}，則LP(G，M，I)是完備格，稱為面向屬性概念格。其上、下確界定義為:?(X1，B1)，(X2，B2)∈ LP(G，M，I)，

(X1，B1)∧ (X2，B2)=(X1∩ X2，(B1∩B2)□◇)，

(X1，B1)∨ (X2，B2)=((X1∪X2)◇□，B1∪B2)。

定義4[9]設(G，M，I)是形式背景，?X?G，B?M，若一個二元組(X，B)滿足X□=B，B◇=X，稱(X，B)為面向對象概念。

記 LO(G，M，I)={(X，B)|X□=B，B◇=X}，則LO(G，M，I)是完備格，稱為面向對象概念格。其上、下確界定義為:?(X1，B1)，(X2，B2)∈ LO(G，M，I)，

(X1，B1)∧ (X2，B2)=((X1∩X2)□◇，B1∩B2)，

(X1，B1)∨ (X2，B2)=(X1∪ X2，(B1∪B2)◇□)。

定義5[11]設(G，M，I)是形式背景，?X?G，B?M，在X和B上定義運算

X+={m∈M|?g∈X，(g，m)?I}，

B+={g∈ G|?m ∈B，(g，m)?I}。

設(G，M，I)是形式背景，?X?G，B?M，若滿足X+=B且X=B+，則(X，B)是補背景(G，M，Ic)的概念。補背景(G，M，Ic)的全體概念記為L(G，M，Ic)。?(A1，B1)，(A2，B2)∈L(G，M，Ic)，定義

(A1，B1)∧ (A2，B2)=(A1∩ A2，(B1∪B2)'*)，

(A1，B1)∨ (A2，B2)=((A1∪A2)*'，B1∩B2)，

則L(G，M，Ic)是完備格，稱為補背景的概念格。

2 基于包含度的4種概念格構造方法

本節主要基于包含度定義了新算子，當包含度取不同的值時，新算子就是*，'，+，◇，□，算子，由此可以構造經典概念格、補背景概念格、面向對象概念格和面向屬性概念格。

定義6[10]設(X，≤)是偏序集，若對于任意x，y∈X，都有數D(y/x)與之對應，且滿足:

1)0≤D(y/x)≤1，

2)x≤ y? D(y/x)=1，

3)x≤ y≤z? D(x/z)≤ D(x/y)，則稱D為X上的包含度。

設G是有限集，Π(G)表示G上的全體子集，“?”表示集合的包含關系，則(Π(G)，?)為偏序集。?E∈Π(G)，F∈Π(G)，記則根據包含度的定義可知，D為Π(G)上的包含度。

定義7 設(G，M，I)是形式背景，?X≠?，X?G，B≠?，B?M，在X和B上定義運算(0≤α≤β≤1):

定義8 設(G，M，I)是形式背景，?X?G，B?M，在X和B上定義運算(0≤α≤β≤1):

例1 表1給出的形式背景(G，M，I)來源于匈牙利的科教電影“生物與水”［2］。這里的對象是電影中提及的生物，屬性是電影所強調的特性。對象和屬性代碼意義如下:①螞蝗，②魚，③蛙，④狗，⑤水草，⑥蘆葦，⑦豆，⑧玉米;a:在水中生活，b:在陸地生活，c:有葉綠素，d:雙子葉，e:單子葉，f:能運動，g:有四肢，h:哺乳。

表1 科教電影“生物與水”的形式背景(G，M，I)Tab.1 Formal context(G，M，I)of science and eduration filum"Biology and Water"

考察表1的形式背景 (G，M，I)。若設 α =0.5，β=1，則根據定義7和定義8可得:

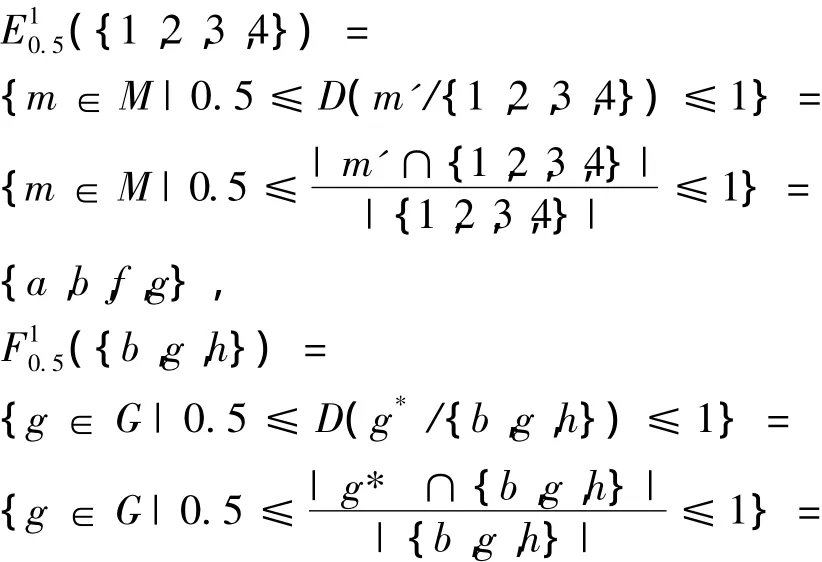
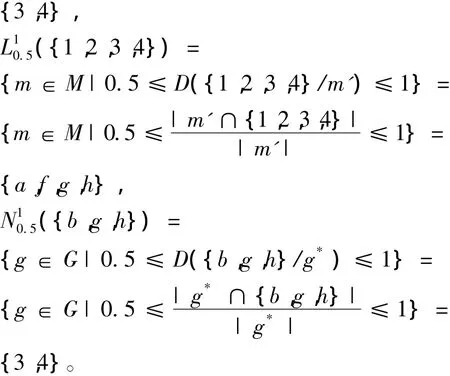
根據定義7和定義8，可得如下結論。

性質1 當［α1，β1］?［α2，β2］時，以下性質成立

例2 考察形式背景表1。若取［α1，β1］ =［0.5，1］，［α2，β2］ = ［0.25，1］，則計算可得

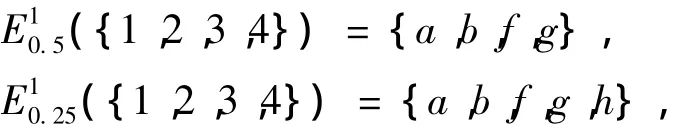
因此

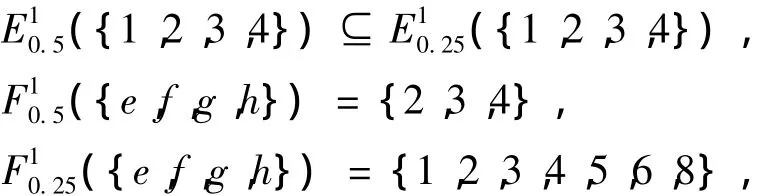
因此

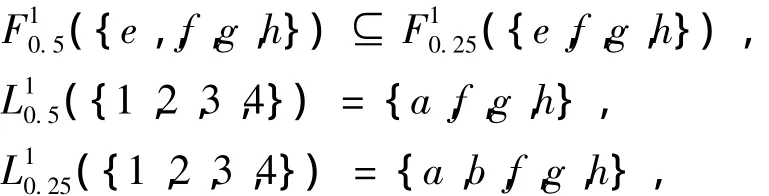
因此

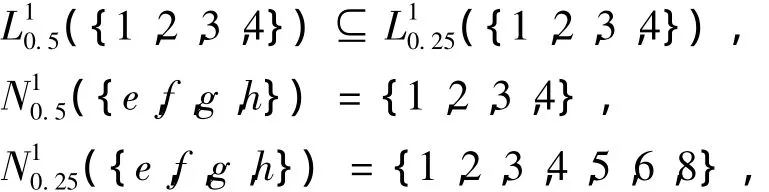
因此

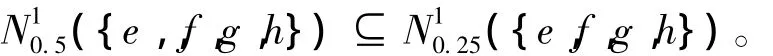
定理1 設(G，M，I)是形式背景，?X?G，B?M，0≤α≤β≤1，有

證 明1)E11(X)={m∈M|D(m'/X)=1}=

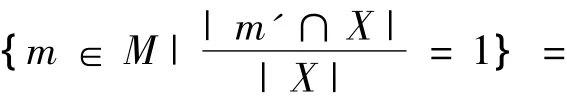
{m∈M|X?m'}=X*，

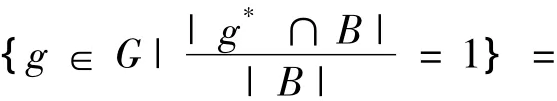
{g∈ G|B ? g*}=B'。

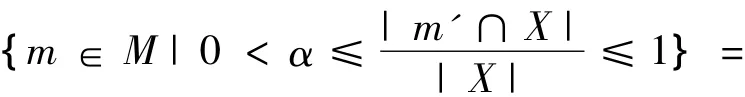
{m∈M|X∩m'≠?}=X◇。

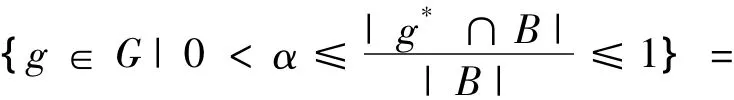
{g∈G|B∩g*≠?}=B◇。

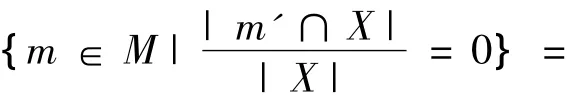
{m∈M|m'∩X=?}=X+，

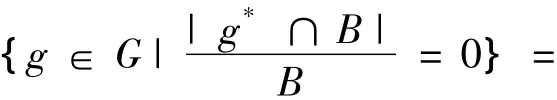
{g∈G|g*∩B=?}=B+。

定理2 設(G，M，I)是形式背景，?X?G，B?M，0≤α≤β≤1，有

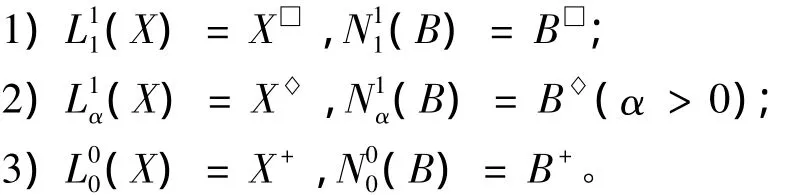
證 明1)L11(X)={m∈M|D(X/m')=1}=

{m∈M|m'?X}=X□，

N11(B)={g∈G|D(B/g*)=1}=

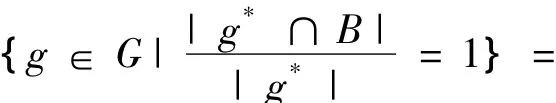
{g∈G|g*?B}=B□。

2)L1α(X)={m∈M|α≤D(X/m')≤1}=

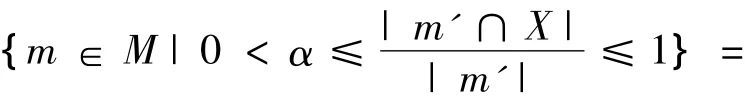
{m∈M|X∩m'≠?}=X◇，

N1α(B)={g∈ G|α ≤ D(B/g*)≤1}=

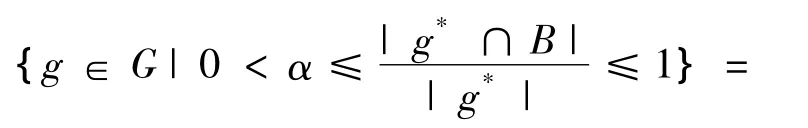
{g∈G|g*∩B≠?}=B◇。

3)L00(X)

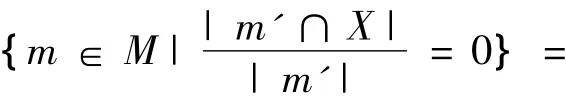
{m∈M|X∩m'=?}=X+，

N00(B)={g∈G|D(B/g*)=0}=

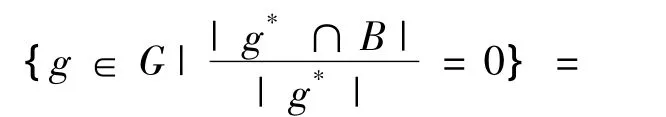
{g∈G|B∩g*=?}=B+。

可由以上定理以及已有的*，'，+，◇算子的性質［2，6，11］，得出以下結論。

推論1 設(G，M，I)是形式背景，?X1，X2，X?G，B1，B2，B?M，以下性質成立

(Ⅰ)當α=β=1時

由定理1與定理2知，當α，β取特定的值時，Eβα，Fβα算子對應著形式背景的概念格與補背景概念格中的算子，因而可以構造相應概念格。類似地，Lβα，Nβα算子對應補背景概念格、面向對象概念格與面向屬性概念格中的算子，因而可以構造這3種格。具體方法如下定理所示。

定理3 設(G，M，I)是形式背景，?X?G，B?M(0≤α≤β≤1)，則

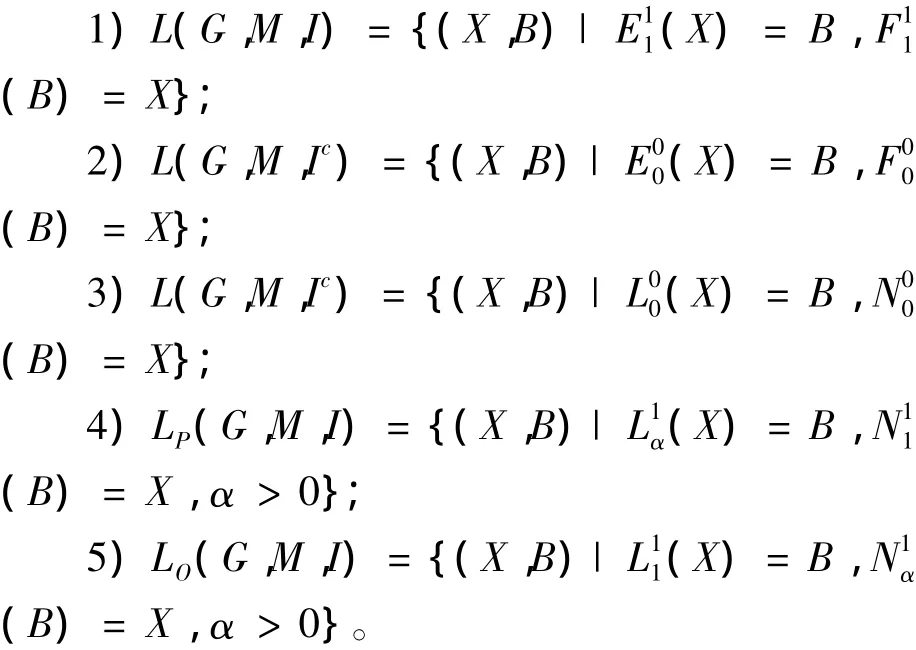
3 結語

本文基于包含度理論定義了新的算子，并證明了當包含度取不同的值時，利用新算子可以構造4種概念格，即經典概念格、補背景概念格、面向屬性概念格和面向對象概念格。這種基于包含度方法是對這4種概念格構造方法的統一。

[1]WILLE R.Restructuring lattices theory:an approach based on hierarchies of concepts[C]∥RIARAL I，Ordered Sets.Dordrecht:Reidel，1982:445-470.

[2]GANTER B，WILLE R.Formal Concept Analysis[M].Mathematical Foundations，New York:Springer-Verlag，1999.

[3]CARPINETO C，ROMANO G.Concept Data Analysis:Theory and Application [M].Chichester:John Wiley＆Sons，Ltd，2004.

[4]HO T B.Discovering and using knowledge from unsupervised data[J].Decision Support System，1997，21(1):29-42.

[5]BELOHLAVEK R.Fuzzy closure operators[J].Journal of Mathematical Analysis and Applications，262(2001)473-489.

[6]DUNTSCH I，GEDIGA G.Approximation operators in qualitative data analysis[C]∥In:Theory and Application of Relation of Structures as Knowledge Instruments，2003:216-233.

[7]YAO Y Y.A comparative study of formal concept analysis and rough set theory in data analysis[J].Lecture Notes in Artificial Intelligence，2004，3066:59-68.

[8]YAO Y Y.A partition model of granular computing[J].Lecture Notes in Computer Science，2004，3100:232-253.

[9]YAO Y Y.Concept Lattices in Rough Set Theory[C]∥DICK S，KURGAN L，PEDRYCZ W，et al.Proceedings of 2004 Annual Meeting of the North American Fuzzy Information Proceeding Society Washington:IEEE Computer Society，2004:796-801.

[10]張文修，梁怡.不確定性推理原理[M].西安:西安交通大學出版社，1996.

[11]何苗，魏玲.基于原背景的補背景概念獲取[J].計算機科學，2012，39(11):197-200.