基于近似對沖的亞式期權定價模型與實證分析

袁國軍， 肖慶憲

（1.上海理工大學管理學院，上海 200093；2.皖西學院經濟與管理學院，六安 237012）

基于近似對沖的亞式期權定價模型與實證分析

袁國軍1，2， 肖慶憲1

（1.上海理工大學管理學院，上海 200093；2.皖西學院經濟與管理學院，六安 237012）

考慮了標的股票的價格服從跳-擴散過程的亞式定價問題.利用無套利原理和廣義Ito公式，運用近似對沖跳躍風險的方法，建立了跳-擴散過程中算術平均亞式期權的定價模型.然后，通過變量代換，將超拋物型偏微分方程變為一般拋物型方程，基于半離散化方法，給出了基于半離散化的差分求解方法，并且對差分格式的穩定性和誤差進行了分析.最后，以北歐電力交易所曾經交易過的亞式期權為例，對亞式期權定價進行了實證分析.

跳-擴散過程；亞式期權；近似對沖；數值方法

亞式期權是目前OTC（柜臺交易）市場上最受投資者歡迎的金融衍生產品，其最早是由美國銀行家信托公司（Bankers Trust）于20世紀90年代在日本東京推出，故稱為亞式期權.最初設計開發亞式期權的目的是用于防止市場上的操縱行為，尤其是期權到期前的操縱行為.后來，針對法人治理結構下現代公司的“內部人控制”問題，引入了亞式期權，對公司經理人采用基于亞式期權的經理人激勵機制，較好地解決了“內部人控制”問題.與歐式期權相比，亞式期權不但具有套期保值的功能，而且還具有價格便宜、可以盡可能減少市場操縱和內幕交易的優點.因此，關于亞式期權的研究成為企業界和理論界的熱點問題之一.

亞式期權實際上是一種路徑相依期權，期權到期日的收益依賴于部分或整個期權有效期內標的資產所經歷的價格的平均值.交割價以幾何平均和算術平均最為常見.Cox等［1］首次給予亞式期權定價方法，通過引入路徑相依變量，給出了亞式期權定價的二叉樹方法.Barraquand［2］給出了二叉樹方法修正的前移打靶格子方法.基于交易賬戶的思想，Shreve等［3］通過對標的證券的自融資交易復制期權對亞式期權進行定價.Hoogland等［4］采用半解析的方法來處理標的證券支付紅利的亞式期權定價問題.另外，亞式期權的定價方法還有：基于偏微分方程求解法［5-6］、Monte Carlo模擬法［7］、傅里葉變換法［8］、近似解析法［9］和上下界法［10］等.

然而，上述關于亞式期權的定價方法都是基于標的資產的價格服從幾何布朗運動給出的，只適用于資產價格的連續變化情況.但在金融實踐中，一些重大信息的到達會對標的資產的價格變化造成劇烈的波動，出現大幅的跳躍現象.因此，幾何布朗運動不能很好地刻畫資產價格的變化情況，尤其是跳躍現象.Merton［11］首次用Poisson過程來刻畫價格的跳躍現象，假設標的資產的價格服從Poisson 跳-擴散過程.Halluin等［12］研究了跳-擴散模型中具有固定執行價格的亞式期權定價問題.Fusai等［13］對Levy過程下的離散亞式期權的定價進行了研究，并且給出了幾何平均亞式期權的傅里葉變換形式的封閉解和算術平均亞式期權的遞歸算法.Chou等［14］研究了跳-擴散模型中的亞式期權定價問題，得到了類似于B-S模型中的亞式期權價格的封閉解，推廣了連續情形下的B-S模型.Kim等［15］運用二叉樹方法給跳-擴散模型中亞式期權進行定價，并且討論了二叉樹方法的收斂性.Hubalek等［16］在標的資產價格同時具有隨機波動率和跳躍的假設下，給出了幾何平均亞式期權價格的半顯式公式.劉宣會等［17］分別在完全市場與不完全市場上，通過選擇賬戶折算變換與復制，將跳-擴散模型中一種算術平均亞式期權定價問題簡化為一種類似歐式期權的定價問題，然后運用Merton對沖風險方法得到了原亞式期權的定價和套期保值策略.張靜等［18］討論了跳躍-擴散模型下亞式期權的定價問題，得到了具有固定執行價格算術平均亞式期權的價格下界公式，并且通過數值計算驗證了該下界公式可以作為亞式期權定價的近似公式.孔文濤等［19］運用總體最小二乘擬蒙特卡洛方法為帶跳市場中隨機利率下的美式-亞式期權定價，并將得到的定價結果和不帶跳市場中的美式-亞式期權的價格進行了比較.韓響楠等［20］在標的資產價格服從跳-擴散過程的假設下，給出了具有固定執行價格亞式期權和浮動執行價格亞式期權價格的一個下界.魏正元［21］在跳躍-擴散過程模型限定下，運用It?-Skorohod微分公式和等價鞅測度變換，得到了歐式加權幾何平均亞式期權封閉形式的解析定價公式.

盡管Black-Schole與Merton模型已成功應用到金融市場，但是近來經驗研究表明：在刻畫資產價格波動上，它們與實際還存在較大偏差.主要表現為：a.跳風險是不容忽視的，可能蘊涵了某種重要的經濟現象；b.資產收益分布可能具有非對稱、尖峰厚尾特征以及“隱含波動率微笑”.近幾十年來，很多研究都是通過解釋Black-Scholes模型的這兩個缺陷來修正Black-Scholes公式，但是這些模型也沒能很好地體現資產收益的尖峰厚尾和非對稱特征，特別是尖峰厚尾特征.Kou［22］的研究發現，已有的跳-擴散模型不能很好地反映金融市場的實際情況，于是他提出了一種新的跳-擴散模型，認為跳躍的密度函數服從雙指數分布.該模型最主要的特點就是能產生一個尖峰厚尾分布，雙指數跳-擴散模型能夠很好地體現資產收益的經驗特征：尖峰厚尾特征和期權定價中的“波動率微笑”.Kou等應用均衡理論，研究了雙指數跳-擴散過程下的期權定價問題，分別得到了標準歐式期權定價公式、美式期權近似定價公式和幾種路徑依賴型期權的定價公式.Park［23］討論了雙指數跳-擴散模型中回望期權二叉樹方法的收斂性問題；鄧國和等［24-25］分別研究了連續支付紅利的雙指數跳-擴散模型中美式兩值現金或無看漲期權的定價問題和CIR隨機波動率與Kou 雙指數跳-擴散組合模型的美式期權函數及最佳實施邊界的性質.（4）

目前文獻中關于跳-擴散模型中期權定價采用的方法主要有：鞅方法、隨機微分方程法、一般均衡理論法和Merton對沖法等.但Merton對沖法只是對沖Brown運動的風險，對Poisson跳躍通常采用取其期望的方法.跳躍行為發生的頻率雖然很小，然而一旦發生，將會對股票、債券及金融衍生產品市場產生巨大的沖擊.歷史上股票市場上多次崩盤事件的發生均是由股票價格的向下大幅劇烈波動造成的.所以，在跳-擴散期權定價模型中，跳躍部分的風險必須給予高度的重視，盡量考慮到跳躍風險對期權價格的影響.因此，本文采用近似對沖跳躍風險的方法，并且運用證券組合技術和無套利原理建立了標的資產價格服從Kou 跳-擴散過程的算術平均亞式期權的定價模型，并且討論了該定價模型的數值解法及其穩定性和誤差等問題.

1 基于近似對沖跳躍風險的亞式期權定價模型

設St為一個風險資產的價格過程，在給定的概率空間（Ω，F，P）中，滿足下列隨機微分方程

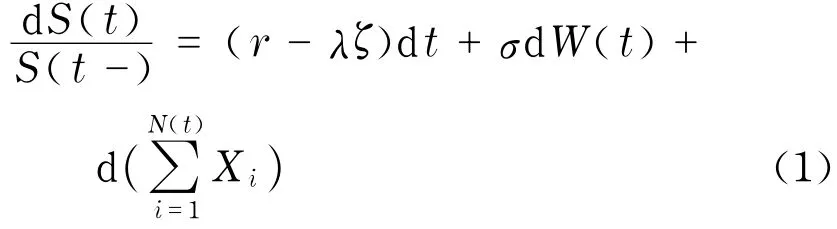
式中，無風險利率r、波動率方差σ2為常數；ζ= E［Xi］；W（t）是一個標準Brownian運動；N（t）是跳躍強度為λ的Poisson過程；W（t），N（t），｛Xi｝相互獨立，且｛Xi｝是獨立同分布的隨機變量，具有對數雙指數密度函數

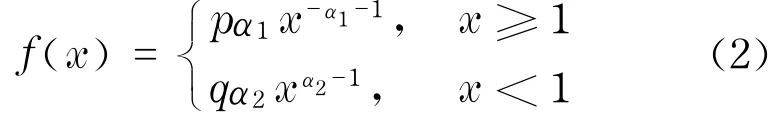
式中，α1，α2分別為兩個指數分布的參數，且α1＞1；p，q分別為價格向上跳躍和向下跳躍的概率，且p+q=1.

設期權的有效期為T，對于任意時刻0≤t≤T，期權的價格V是標的資產價格S、路徑變量J和時間t的函數，記為V=V（S（t），J，t）.期權賣出方在t時刻持有Δ份風險資產，以期對沖在期權到期日T時刻損失V=V（S，J，T）的風險，即花費了ΔS，于是在t時刻該組合的價值為

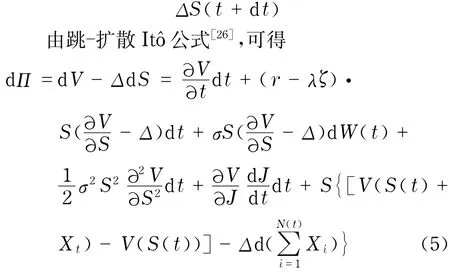
Poisson過程N（t）在d t時間內有一次跳躍的概率是λd t，超過一次的概率是o（d t）.因此，如果d t足夠小，可以忽略多次跳躍，并有

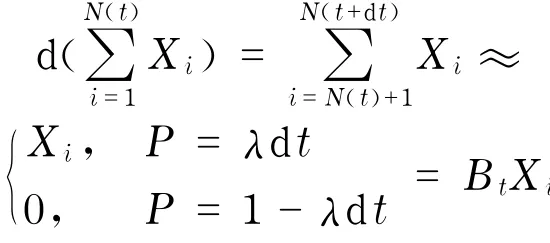
其中，Bt為Bernoulli隨機變量，且P（Bt=1）= λd t，P（Bt=0）=1-λd t，Xi是跳躍幅度，服從對數雙指數分布.由Taylor公式得

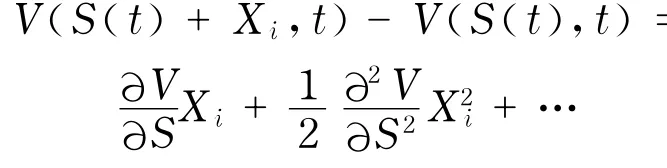
若時間的變化d t足夠小，標的資產的價格要么發生一次跳躍，要么沒有跳躍.分別求出沒有跳躍和有一次跳躍時期權的價格，再以發生跳躍與否的概率作為權重求出跳-擴散模型中亞式期權的價格.

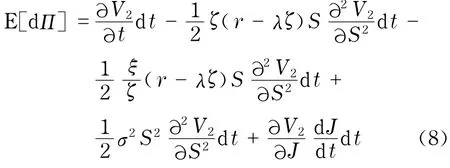
根據期權定價的無套利原理，則投資組合的期望收益等于其無風險收益，即：E［dΠ］=rΠd t，則

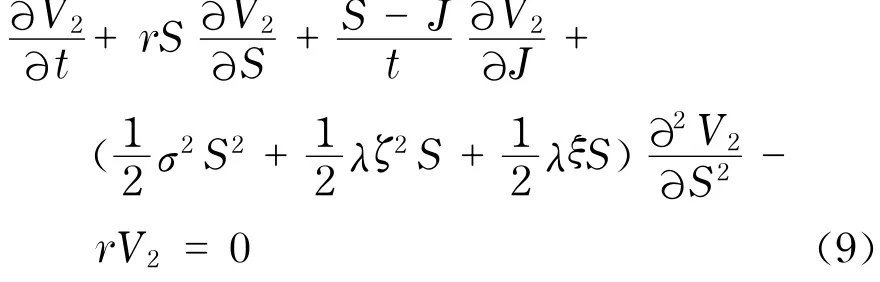
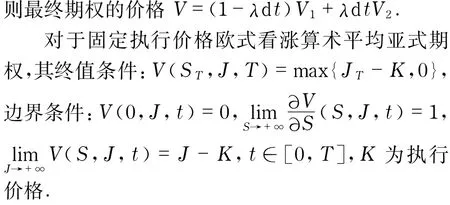
2 數值解法

若標的資產價格服從幾何布朗運動，幾何平均亞式期權有解析解，而算術平均亞式期權則沒有解析，通常用二叉樹方法、均值關系近似方法、二階矩近似方法、Monte Carlo模擬方法等來求解算術平均亞式期權定價模型.Boyle［7］采用Monte Carlo方差控制方法，以幾何平均為標的的亞式期權作為初始值，導出了算術平均亞式期權的近似解.基于線性過程的方法，Bouaziz［27］給出了平均執行價格亞式期權的近似解.利用對數正態分布近似算術平均的真實分布來作為算術平均近似的分布，Lévy［28］給出了算術平均亞式期權定價的近似解.Simon［29］給出了算術平均亞式期權的近似解及模擬方法.

對于跳躍過程服從復合Poisson過程下的亞式期權更是沒有解析解.另外，由于亞式期權具有避免人為操縱、內部交易等優點，在目前的期權OTC市場上深受投資者歡迎.與幾何平均相比，算術平均更容易理解，在期權OTC市場上，以算術平均亞式期權表現最為活躍.因此，研究其數值解更具有實踐意義和應用價值.這里主要討論了跳躍過程服從復合Poisson過程的Kou 跳-擴散模型中算術平均亞式期權定價的數值解法問題.

對于線性拋物型偏微分方程，求解的數值方法有有限元法、有限差分法等.拋物型偏微分方程在某種意義上是常微分方程的擴展［30］.因此，可以僅對空間導數離散化，將偏微分方程近似轉化為一個常微分方程組，這種方法稱為半離散化方法［30］.這里，僅給出式（9）的半離散化差分格式，式（6）的半離散化差分格式及其穩定性和誤差分析等結果同理可得.

由于式（9）是一個含有3個變量的超拋物型偏微分方程，為了給出其簡單易行的數值方法，先通過適當的變換，把它變為一般的拋物型偏微分方程.首先給出變換

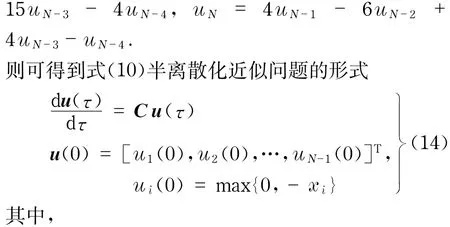
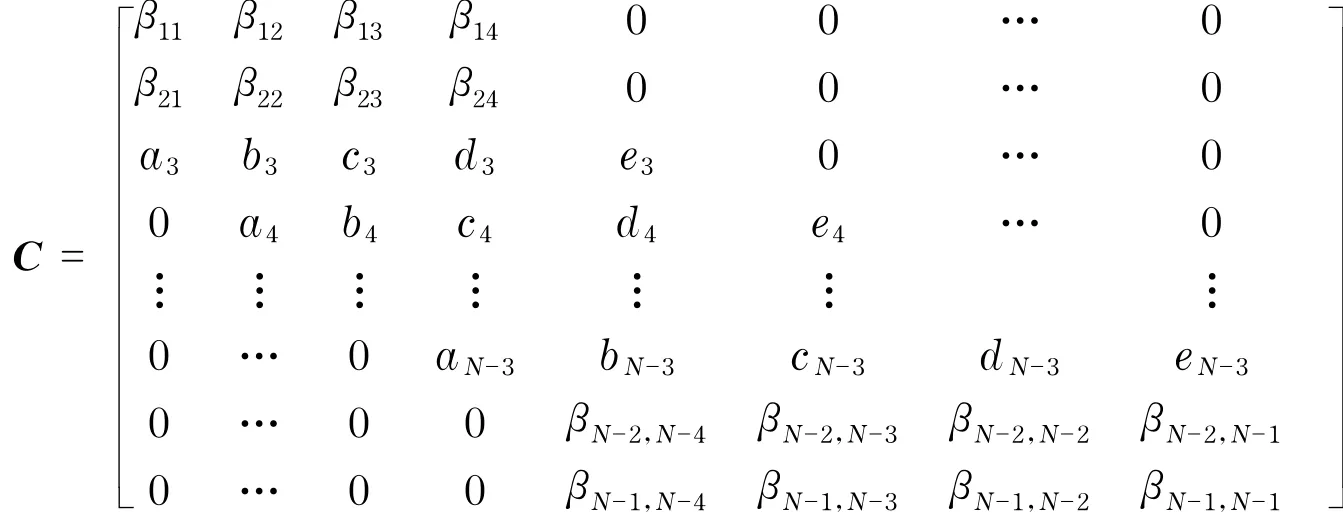
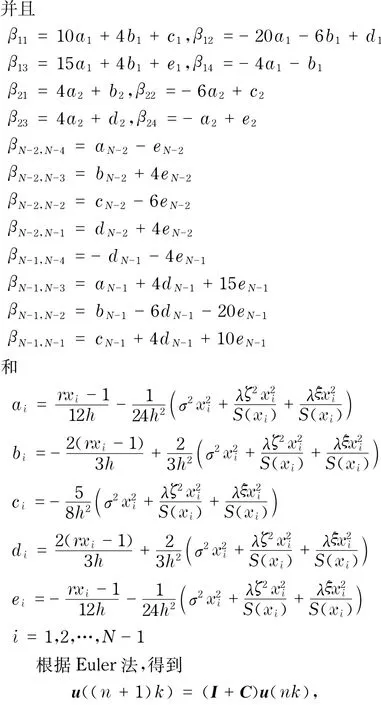
其中，I是N-1階單位矩陣，k=Δt，lk=τ=T-t，則式（15）向量初值問題的數值解為

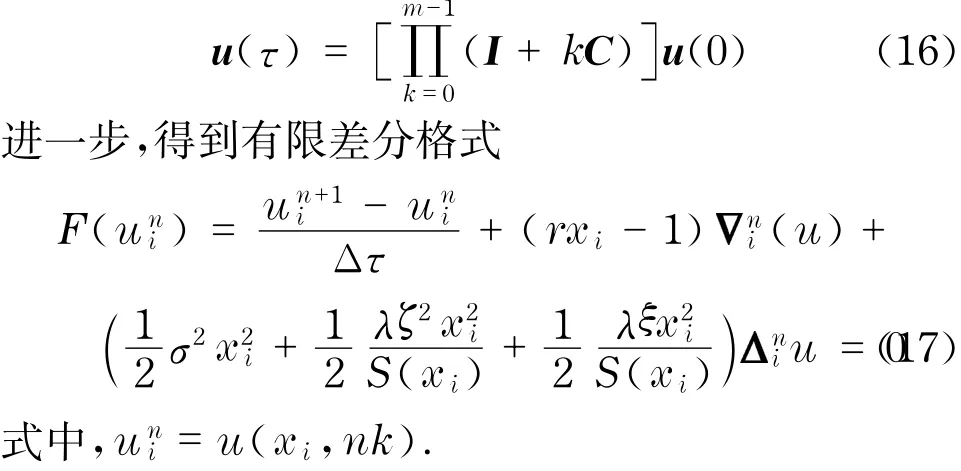
3 差分格式的穩定性分析

本節討論對于固定的h=Δx＞0，有限差分格式對時間的穩定性.即h=Δx固定時，當k=Δτ，l→+∞，且lk=τ時，解u（τ）仍是有界的.

當h固定時，矩陣C也是固定的，則矩陣C可以分解為

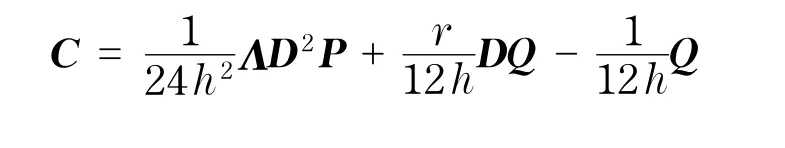
式中，Λ和D是對角陣，且

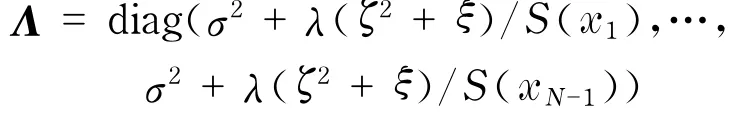
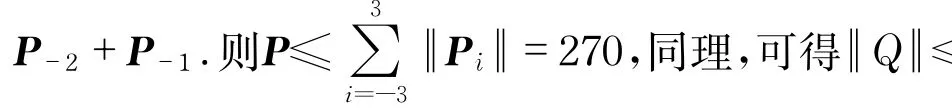
4 差分格式的誤差分析

對于一個有效的差分格式，當分割越來越細時，其截斷誤差應趨于零，亦即意味著差分格式的精確解能夠很好地趨向于偏微分方程理論上的精確解.

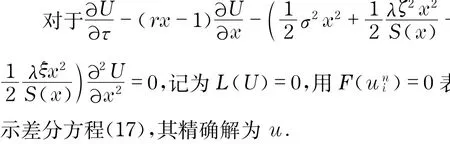
令Tni（U）=F（Uni）-L（Uni），若當h=Δx→0，k=Δτ→0時，Tni（U）→0，則稱差分格式的誤差有界，也即差分格式是收斂的［31］.其中，Uni表示方程（11）在點（xi，nk）處的理論值，即Uni=U（xi，nk）.如果Tni（U）=O（hp）+O（kq），則稱差分格式的截斷誤差是O（hp+kq）［31］.

對于差分格式的內點，則有

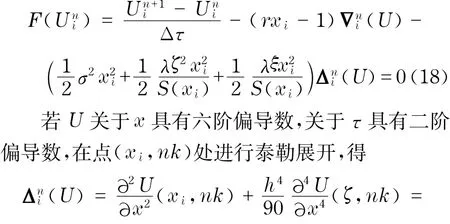
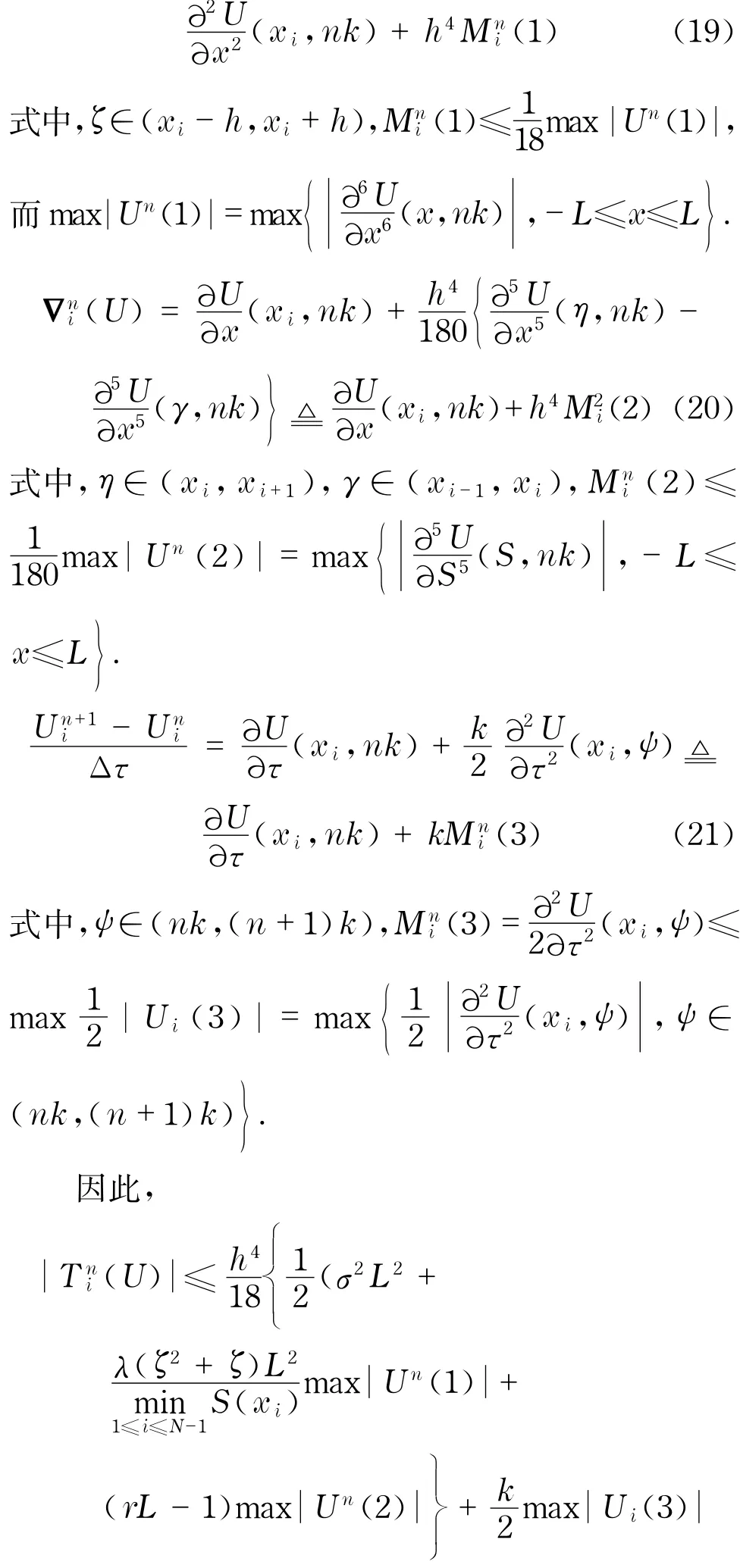
所以差分格式式（17）的截斷誤差有界，且Tni（U）= O（h4）+O（k）.

5 實證分析

北歐電力交易所（Nord Pool）的期權交易開始于1999年10月29日，提供兩種類型可供交易的期權：歐式電力期權（EEO或EPO）和亞式電力期權（AEO或APO）.其中亞式電力期權的標的資產是在北歐電力交易所交易的標準的電力期貨合約，亞式電力期權是根據現貨電價市場的系統電價的算術平均值進行自動執行和結算的.如果平均系統平均電價和執行價格的價差為正（負），則買入（賣出）的亞式電力期權是盈利的，在結算期的最后一個交易日后進行結算；如果是“價格不變”或是“賠錢的”，則不發生支付行為.因此，亞式電力期權本質上就是金融衍生品中的亞式期權.另外，亞式電力期權是北歐電力交易所中一個特殊且重要的電力衍生產品.一是因為它是唯一在交易所交易的亞式期權；二是盡管它滿足了投資者在不穩定電力市場上進行套期保值的需求，但是可能基于較低的流動性，北歐電力交易所后來終止了其交易.

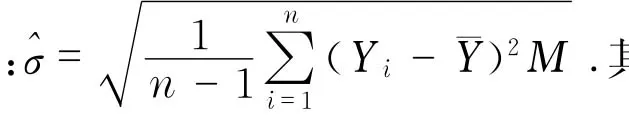
用U1表示標的資產價格向上跳躍的百分比，U2表示標的資產價格向下跳躍的百分比，假設U1，U2均是在一定的有限區域上服從對數雙指數分布.規定當系統電價上升（下降）超過3%時，跳躍即發生.這里假設U1的取值范圍為U1∈［0.03，0.1］，U2的取值范圍為U2∈［-0.1，-0.03］.將系統電價的樣本看成是有序樣本，根據上面假設，由市場數據，很容易找到相應的跳躍點.若U1發生了n1次，U2發生了n2次，則跳躍強度λ的估計為λ=（n1+n2）／n.根據樣本計算，n1=84，n2= 110，故λ=0.535 5.另外，根據樣本數據，可以計算出跳躍的平均幅度ζ=0.016，跳躍幅度的方差為ξ=0.191 6，無風險利率取r=0.032 5.

為了檢驗本文模型和計算方法的有效性和期權價格對poisson跳躍分布的穩健性，利用本文的定價模型及差分算法計算出1999年11月25日至2000年1月3日19個交易日（共26個交易日，舍去了7個明顯異常的數據）的亞式電力期權（AEOGB0300）的價格.圖1給出了不同交易日的本文計算價格、Merton模型價格、對數均勻分布價格與市場價格計算結果的比較.

從圖1可以看出，用本文模型和方法計算的亞式電力期權的價格比用Merton模型和跳躍服從對數均勻分布模型計算的價格更接近市場的實際價格.另外發現，亞式電力期權的價格對poisson跳躍分布具有較大的敏感性，與對數正態分布和對數均勻分布相比，期權價格對對數雙指數分布更敏感，其計算的期權價格更接近市場價格.

圖2給出了亞式電力市場價格、計算價格及標的資產（電力期貨合約）價格變化趨勢.從圖2可以看出，采用本文的模型和方法計算的期權價格變化趨勢和標的資產價格變化的趨勢幾乎完全吻合（僅出現一次不吻合）.隨著每個時間點上標的資產價格的漲跌，該期權的理論價值也會立即產生相應的漲跌，但是變化的幅度大于標的資產的變化幅度（因為標的資產——電力期貨合約的價格較高），而市場價格卻出現了6次變化趨勢與標的股價變化趨勢相反的情況.因此，本文模型和方法計算的價格對標的資產價格的敏感度要高于市場價格對標的資產價格的敏感度.

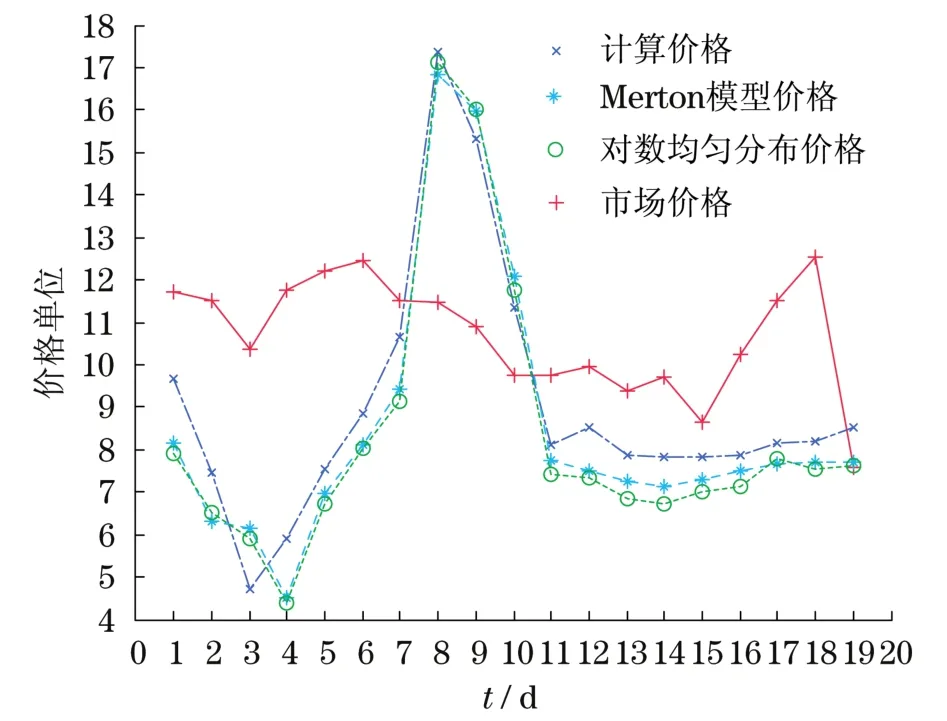
圖1 幾種模型價格與市場價格的比較Fig.1 Comparison of several models’prices with market prices

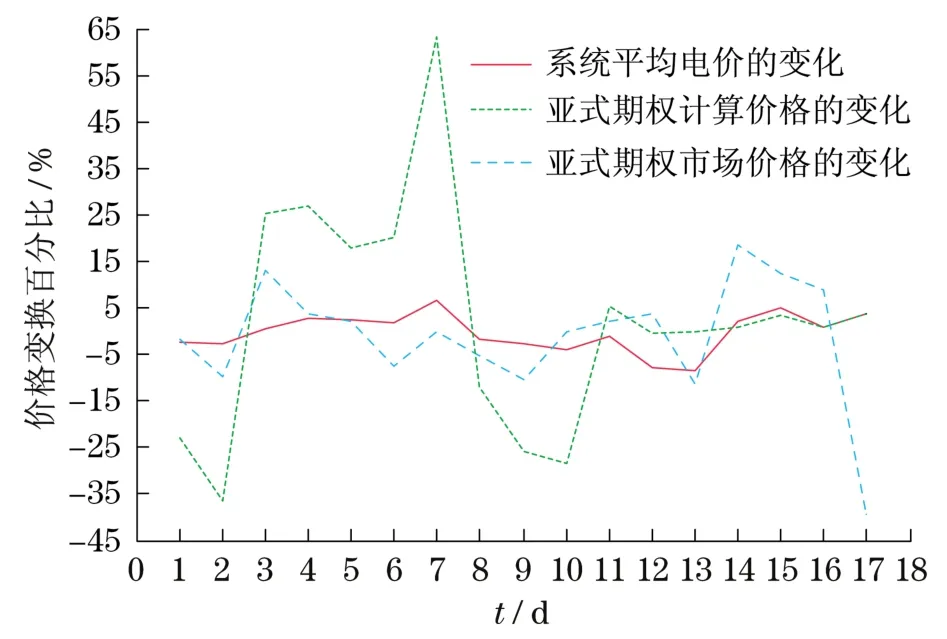
圖2 亞式電力期權市場價格、計算價格及標的期貨合約價格變化趨勢比較Fig.2 Changing trend comparison between the market price，calculated price and futures contract price of Asian eletricity options

6 結束語

基于近似對沖跳躍風險的方法，本文建立了標的資產價格服從跳-擴散過程的歐式固定執行價格算術平均亞式期權的定價模型.給出了基于半離散化的差分求解方法，并且對差分格式的穩定性和誤差進行了分析.在最后的實證分析部分，以北歐電力交易所曾經交易過的亞式電力期權為例，對亞式期權的定價進行了實證分析.

致謝本文作者衷心感謝波蘭Wroclaw大學Rafal Weron教授提供了北歐亞式電力期權數據.

［1］ Cox JC，Ross S A，Rubinstein M.Option pricing：a simple approach［J］.Journal of Finance Economics，1979，7（2）：229-263.

［2］ Barraquand J，Pudet T.Pricing of American pathdependent contingent claims［J］.Mathematical Finance，1996，3（1）：17-51.

［3］ Shreve S，Vecer J.Options on a trade account：vacation calls，vacation puts and passport options［J］.Finance and Stochastics，2000，8（4）：255-274.

［4］ Hoogland J K，Neumann C D.Local scale invariance and contingent claim pricing［J］.International Journal of Theoretical and Applied Finance，2001，4（1）：1 -21.

［5］ Rogers L C G，Shi Z.The value of an Asian option［J］. Journal of Applied Probability，1995，32（4）：1077 -1088.

［6］ Dubois F，Lelievre T.Efficient pricing of Asian options by the PDE approach［J］.Journal of Computational Finance，2004，8（2）：55-64.

［7］ Boyle P，Broadie M，Glasserman P.Monte Carlo methods for security pricing［J］.Journal of Economic Dynamics and Control，1997，21（8／9）：1267-1321.

［8］ Benhanou E.Fast fourier transform for discrete Asian options［J］.Journal of Computational Finance，2002，6 （1）：49-61.

［9］ Foschi P，Pagliarani S，Pascucci A.Approximations for Asian options in local volatility models［J］.Journal of Computational and Applied Mathematics，2013，237 （1）：442-459.

［10］ Vanmaele M，Deelstra G，Liinev J，et al.Bounds for the price of discrete arithmetic Asian options［J］.Journal of Computational and Applied Mathematics，2006，185（1）：51-90.

［11］ Merton R C.Option pricing when underlying stock returns are discontinuous［J］.Financial Economics，1976，3（1／2）：125-144.

［12］ Halluin Y D，Forsyth P A，Labahn G.A semi-Lagrangian approach for American Asian options under jump diffusion［J］.SIAM Journal on Scientific Computing，2005，27（1）：315-345.

［13］ Fusai G，Meucci A.Pricing discretely monitored Asian options under Lévy processes［J］.Journal of Banking and Finance，2008，32（10）：2076-2088.

［14］ Chou CS，Lin H J.Asian options with jumps［J］. Statistics&Probability Letters，2006，76（18）：1983 -1993.

［15］ Kim K I，Qian X S.Convergence of binomial tree method for Asian options in jump-diffusion models［J］. Journal of Mathematical Analysis and Applications，2007，330（1）：10-23.

［16］ Hubalek F，Sgarra C.On the explicit evaluation of the geometric Asian options in stochastic volatility models with jumps［J］.Journal of Computational and Applied Mathematics，2011，235（11）：3355-3365.

［17］ 劉宣會，徐成賢.基于跳躍-擴散過程的一類亞式期權定價［J］.系統工程學報，2008，23（2）：142-147.

［18］ 張靜，何春雄，郭艾，等.跳躍-擴散模型下亞式期權的定價［J］.系統工程，2010，28（12）：96-99.

［19］ 孔文濤，張衛國.帶跳市場中隨機利率下的美式-亞式期權定價［J］.系統工程學報，2012，27（3）：338 -343.

［20］ 韓響楠，何春雄.帶跳市場中亞式期權的價格下界［J］.系統工程學報，2010，25（3）：354-359.

［21］ 魏正元.跳躍-擴散型歐式加權幾何平均價格亞式期權定價［J］.應用概率統計，2007，23（3）：238-246.

［22］ Kou SG.A jump-diffusion model for option pricing ［J］.Management Science，2002，48（8）：1086-1101.

［23］ Park H S.Analytical binomial lookback options with double-exponential jumps［J］.Journal of the Korean Statistical Society，2009，38（4）：397-404.

［24］ 鄧國和，黃艷華.雙指數跳擴散模型的美式二值期權定價［J］.高校應用數學學報，2011，26（1）：21-26.

［25］ 鄧國和，楊向群.隨機波動率與雙指數跳-擴散組合模型的美式期權定價［J］.應用數學學報，2009，32（2）：236-255.

［26］ Cont R，Tankov P.Financial modeling with jump process［M］.Boca Raton：Chapman and Hall／CRC，2004.

［27］ Bouaziz L，Briys E，Crouhy M.The pricing of forwardstarting Asian options［J］.Journal of Banking& Finance，1994，18（5）：823-839.

［28］ Lévy E.Pricing European average rate currency options［J］.Journal of International Money and Finance，1992，11（5）：474-491.

［29］ Simon S，Goovaerts M J，Dhaene J.An easy computable upper bound for the price of an arithmetic Asian option ［J］.Insurance：Mathematics and Economics，2000，26 （2／3）：175-183.

［30］ Iserles A.A first course in the numerical analysis of differential equations［M］.London：Cambridge University Press，1996.

［31］ Golub G H，van Loan C F.Matrix cooputations［M］. Baltimore：The Johns Hopkins University Press，1996.

（編輯：丁紅藝）

Pricing Model of Asian Options and Empirical Analysis Based on Approximating Hedge

YUANGuo-jun1，2， XIAOQing-xian1
（1.Business School，University of Shanghai for Science and Technology，Shanghai 200093，China；2.School of Economy and Management，West Anhui University，Lu’an 237012，China）

The Asian pricing was considered when underlying stock price obeys jump-diffusion process.An arithmetic mean Asian options pricing model and a partial differential equation of the pricing model were established by using the generalized It oformula and the no-arbitrage principle，based on the method of approximating hedge jump risk.Then，the ultra parabolic partial differential equation was transformed into a generalized parabolic equation by using variable substitution method.The semidiscretization numerical arithmetic scheme of the partial differential equation derived by means of semidiscretization，and the stability and error analysis of the difference scheme were also discussed.Finally，the empirical analysis of Asian option pricing was carried out，taking the Asian-style electricity options，as an example which have been traded in the Nord Pool.

jump-diffusion process；Asian options；approximating hedge；numerical method

F 830.9；F 224.0文獻標示碼：A

1007-6735（2014）05-0416-09

10.13255／j.cnki.jusst.2014.05.002

2013-09-20

國家自然科學基金資助項目（11171221）；上海市一流學科建設資助項目（XTKX2012）

袁國軍（1981-），男，博士研究生.研究方向：金融工程.E-mail：13865792190＠163.com

肖慶憲（1956-），男，教授.研究方向：金融工程.E-mail：qxxiao＠163.com