艉軸密封裝置Ω彈簧組的多參數優化設計

楊 敏， 柳建華， 吳堂榮

（1.上海理工大學能源與動力工程學院，上海200093；2.中國船舶重工業集團公司第七〇四研究所，上海200031）

艉軸密封裝置Ω彈簧組的多參數優化設計

楊 敏1， 柳建華1， 吳堂榮2

（1.上海理工大學能源與動力工程學院，上海200093；2.中國船舶重工業集團公司第七〇四研究所，上海200031）

Ω彈簧組作為艉軸密封裝置的重要組成部件，其結構補償能力直接影響艉軸密封裝置的密封效果.基于零階算法，以單片彈簧的特征厚度、寬度、中圓半徑和頂圓半徑為設計變量，對Ω彈簧組進行多參數優化分析.通過有限元優化設計，分析求解Ω彈簧組各設計參數的響應以及徑向剛度的最優解，優化后的剛度值比優化前的增加了11.5%.并對優化前后的Ω彈簧組分別進行諧響應分析，驗證了Ω彈簧組徑向剛度的優化設計對改變Ω彈簧組頻率補償能力的有效性，進而改善其結構補償能力.

Ω彈簧組；結構補償能力；零階算法；多參數優化分析；諧響應

近年來，Ω彈簧組在一種新型艉軸密封裝置中得到了廣泛應用.利用Ω彈簧組受壓時所產生的預緊力，使動摩擦副與靜摩擦副之間產生一定的軸向壓力，進而通過運動摩擦副起到端面密封效果.圖1為艉軸密封裝置結構示意圖，該裝置能夠有效補償軸系高速旋轉時產生的軸向、徑向振動，保證艉軸密封端面的平穩密封［1-3］.Ω彈簧的結構補償能力與彈簧組的徑向剛度有直接的關系，徑向剛度越大，其頻率補償能力越強，而對應的幅值補償能力則會受到限制.

眾多學者對改善Ω彈簧的結構補償性能進行了試驗研究.王曉軍等［4］研究了Ω彈簧金屬片的最大應力區、密封結構的剛度曲線、比壓曲線以及振動補償特性.胡舉喜等［5］在此基礎上對其進行優化設計，分別研究了3種金屬彈簧片根部半徑和彈簧片厚度對Ω彈簧組的壽命及補償能力的影響，提出了根圓半徑以及厚度對Ω彈簧剛度、補償能力的影響.艉軸密封裝置工作時，軸系高速轉動所產生的軸向、徑向振動作用于靜環端面，再傳遞至Ω彈簧組結構.Ω彈簧組在安裝時有一定的預壓縮量，所以，對于艉軸密封裝置，其頻率補償能力比幅值補償能力更為重要.因此，本文基于零階優化算法，以Ω彈簧組徑向剛度為目標，對Ω彈簧組進行多參數優化設計，使其具有合適的結構補償能力.

1 算法與模型

1.1 艉軸密封裝置的基本結構

構成艉軸密封裝置的基本元件有固定座、Ω彈簧組、夾緊環、靜環、動環、驅動環和艉軸，如圖1所示.通過Ω彈簧組的軸向補償能力，為艉軸提供軸向密封作用.現主要研究Ω彈簧組對艉軸密封效果的影響.

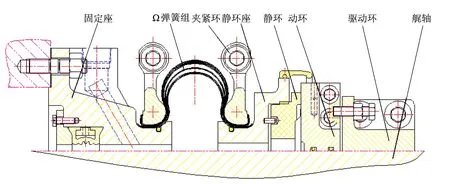
圖1 艉軸密封裝置結構示意圖Fig.1 Schematic diagram of ship seal device

1.2 零階優化算法

Ω彈簧組優化設計時考慮的設計參數較為復雜，同時需要考慮最小安全因子對參數設計的限制，故考慮零階優化算法，其計算流程如圖2所示.零階算法是在一定次數的抽樣基礎上，擬合設計變量、狀態變量和目標函數的響應函數，從而尋求最優解.函數曲線（或曲面）的形式可采用線性擬合、平方擬合或平方加交叉項擬合［6-8］.

采用平方擬合，則目標函數的擬合式為

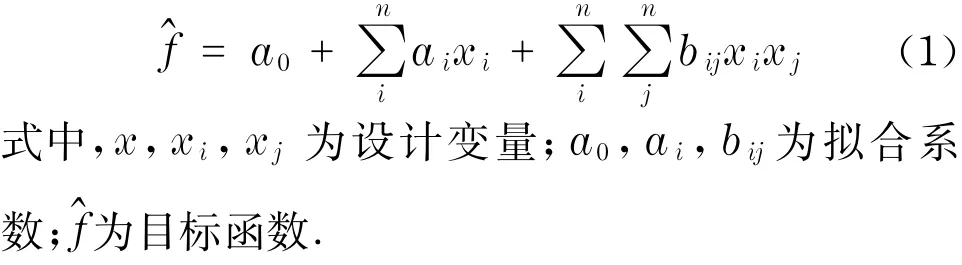
對于設計變量和狀態變量的約束條件，可采用罰函數將其轉化為無約束方程，如式（2）所示，從而將帶有約束的優化問題轉化成無約束的最小值求解問題.

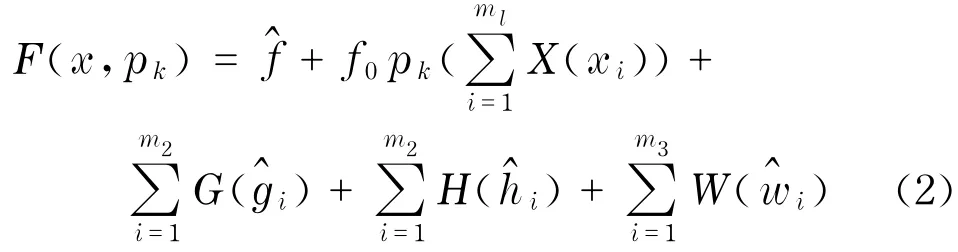
當設計變量（或狀態變量）接近限值時，其罰函數值將急劇增加.

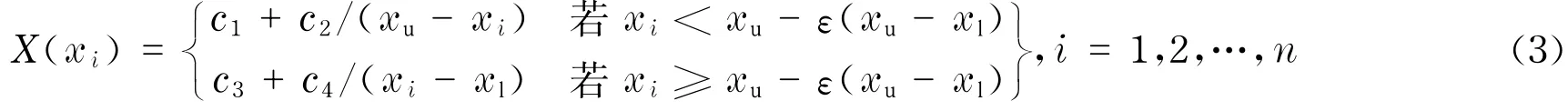
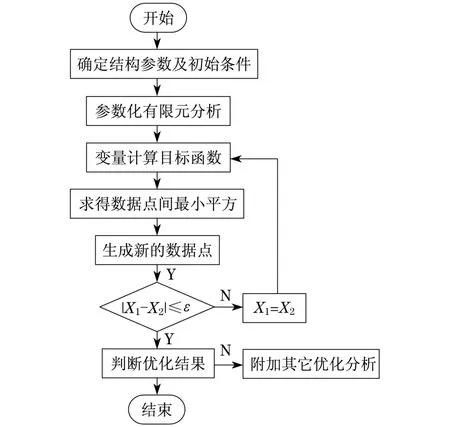
圖2 Ω彈簧組優化流程圖Fig.2 Process flow diagram of optimization forΩspring set

式中，xu，xl為設計變量的上下限；c1，c2，c3，c4為系數；ε是極小的正數.

轉化為無約束問題后，即可采用序慣無約束極小化方法來搜索無約束目標函數.

1.3 有限元模型的建立

采用ANSYS Design Modeler對Ω彈簧組進行參數化建模.常規的單片Ω彈簧采用層合殼單元離散，可以簡化有限元模型［9］，但本文研究的Ω彈簧組由單片支撐彈簧、單片橋接彈簧和單片支架彈簧疊加組成，涉及到鋪層方向上不同單片彈簧層間應力問題，層合板理論和相應的層合板殼單元不再適用.所以，使用3D結構單元Solid185模型對其進行有限元離散，更加準確地反映鋪層之間的應力作用.單元Solid185含有8個節點，每個節點考慮3個自由度，則節點位移

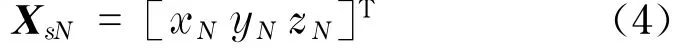
式中，xN，yN，zN分別為節點N沿x，y，z方向的線位移.

1.4 數學模型

艉軸密封裝置工作時受到軸向、徑向振動作用及不穩定水壓影響，會對艉軸密封裝置的彈簧組結構產生位移載荷，Ω彈簧組的控制方程為

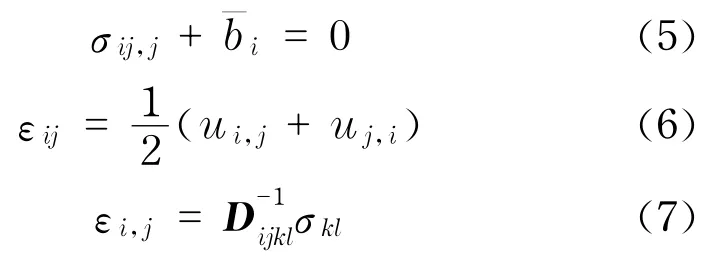
位移邊界條件為

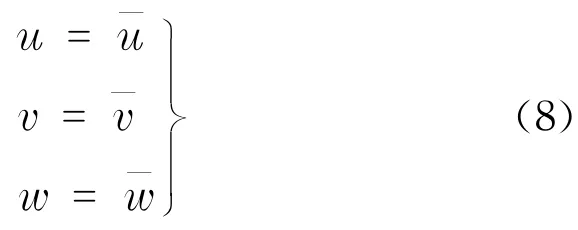
式中，σij，j為應力σij對j方向求偏導數；b表示作用在Ω彈簧組上沿著i方向的單位體積力；ui，j為ui對j方向的偏導數，εij為ioj面內的剪應變；Dijkl為彈性矩陣，可根據Voigt移動規則得出對應關系；為邊界位移；εi，j為應變；σkl為應力；σij為ioj面上的應力；ui為位移分量；u，v，w為臨近表面的位移.

2 多變量優化設計

優化設計是將實際問題首先轉化為最優問題，然后運用最優化原理和方法，從滿足各種設計要求及限制條件的全部可行方案中，選出最優設計參數，獲得最優值.通過最優設計，能夠使零件的力學性能得到改善，并且獲得理想的結構布局和尺寸.

2.1 設計變量及約束條件

Ω彈簧組優化涉及到的設計變量分別為單片彈簧的特征厚度T，寬度W，中圓半徑Rm以及頂圓半徑Rt，如圖3所示.

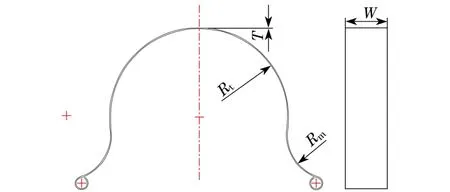
圖3 單片Ω彈簧示意圖Fig.3 Schematic diagram of singleΩspring

Ω彈簧組一般用于艦船艉軸密封等場合，其主要失效方式為屈服失效，故采用最大應力理論和畸變能密度理論進行強度校核.

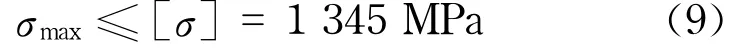
式中，σmax為最大應力；［σ］為許用應力.

由于水下固有環境不同以及沖擊波等突發頻譜的不同，可以根據實際的情況，選擇合適的安全因子.本設計中應該保證最小安全因子ξmin不小于1.45，即

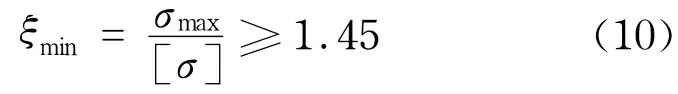
2.2 目標函數

在矩陣位移法中，單元分析的任務是建立單元剛度方程，形成單元剛度矩陣，單元剛度方程為

待優化的Ω彈簧組要求得到最大的徑向剛度，故優化目標函數確立為

式中，Ke為剛度矩陣；qe，Pe分別為位移向量、力向量；Kr為優化目標函數；Ke，r為徑向剛度矩陣.

最終優化數學模型為

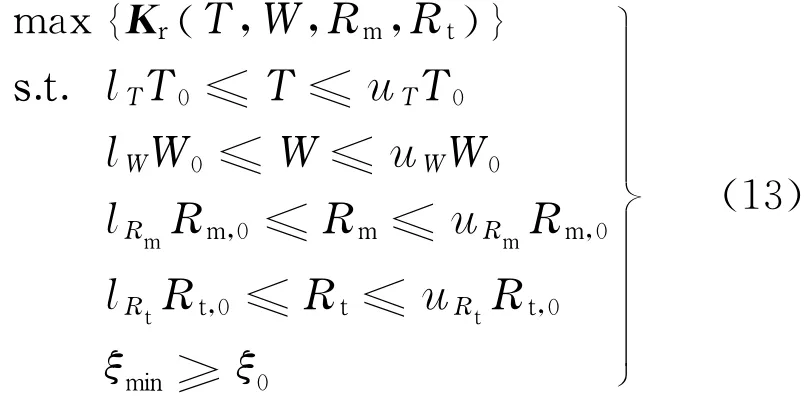
式中，T0，W0，Rm，0，Rt，0分別為Ω彈簧組單片初始特征厚度、寬度、中圓半徑和頂圓半徑；uT，lT，uW，lW，uRm，lRm，uRt，lRt分別代表對應參數的上限、下限系數；ξ0為設計安全因子.

3 優化分析

采用零階方法對優化模型進行參數優化.Ω彈簧組的主體材料是蒙乃爾合金K500，彈性模量為1.78×1011，泊松比為0.32，屈服極限為1 345 MPa，安裝時有20 mm的預壓縮量，各狀態變量的設計上、下限系數分別為（1±10%）.

3.1 優化結果

選取最小安全因子為狀態參數，徑向剛度最小為目標函數，目標驅動優化結果，得到優化結果如圖4所示，徑向剛度與最小安全因子隨著設計參數的改變而發生改變.

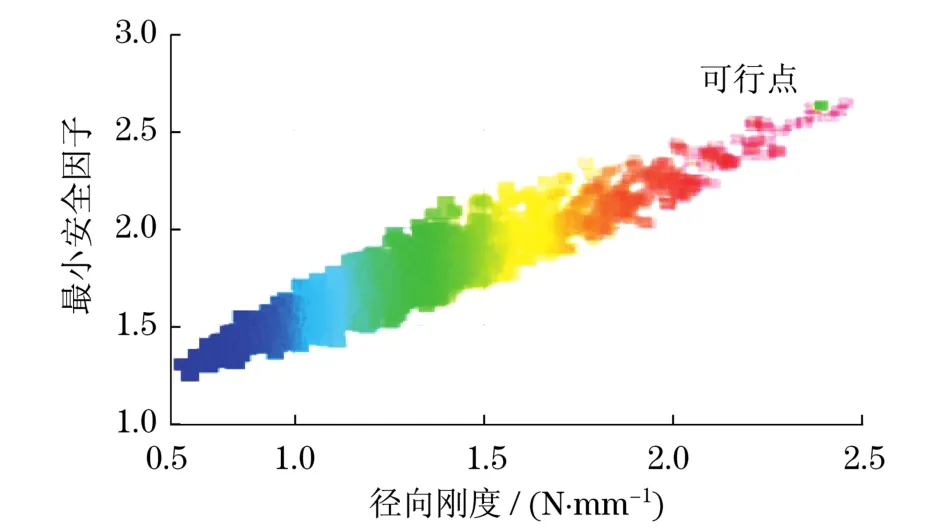
圖4 優化結果權衡圖Fig.4 Balanced figure for optimization results

表1分別列出了優化前后各個參數的取值，可以看出，在保證最小安全因子符合設計要求的情況下，特征厚度和寬度適當增大可以提高Ω彈簧組徑向剛度；同時，中圓半徑增大與頂圓半徑減小對提高Ω彈簧組徑向剛度起到增益作用.徑向剛度由優化前的1 355 N／m增大為1 511 N／m，提高了11.5%，優化效果明顯.

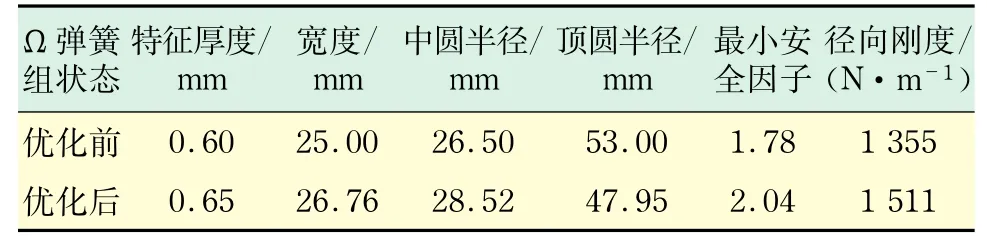
表1 優化前后參數對照Tab.1 Comparison of parameters before and after optimization

3.2 優化前后諧響應分析

為評價多參數優化對Ω彈簧組結構補償能力的影響，在模態分析的基礎上，對優化前后的Ω彈簧組分別進行諧響應分析.諧響應分析主要用于確定線性結構在承受隨時間按正弦（簡諧）規律變化的載荷時的穩態響應，分析過程中只計算結構的穩態受迫振動［10-11］.

分析結果如圖5所示，Ω彈簧組優化前在不同頻率的最大響應幅值為22 mm，優化后可補償最大響應幅值減小為13 mm，但同時其頻率響應范圍變大，即頻率補償能力增強，進一步驗證了提高Ω彈簧組的徑向剛度可以改善其結構補償能力.

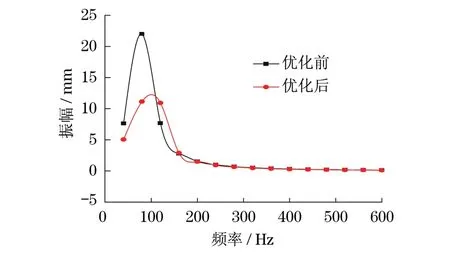
圖5 優化前后諧響應圖Fig.5 Harmonic response figure

4 結 論

a.基于零階算法，以徑向剛度為優化設計目標，建立Ω彈簧組多參數優化設計模型，實現了結構補償能力的優化.

b.Ω彈簧組的特征厚度、寬度、中圓半徑增加，頂圓半徑減小，可以提高Ω彈簧組的徑向剛度.

c.通過優化前后Ω彈簧組的諧響應分析，驗證了優化設計的有效性.結果表明，提高Ω彈簧組的徑向剛度能有效地提高Ω彈簧組的頻率補償能力，進而改善其結構補償能力.

［1］ 周斌興，劉步豐，胡年豐.新型船舶艉軸端面密封裝置的結構與設計［J］.船舶工程，2009，31（2）：24-26.

［2］ 周斌興，張能武.船舶艉軸密封Ω型彈性元件的設計與應用［J］.船海工程，2006（6）：60-62.

［3］ 王瑾，王亞斯，段文珊，等.船舶艉軸密封裝置動態環境下的熱態性能模擬分析［J］.上海理工大學學報，2013，5（4）：361-364.

［4］ 王曉軍，胡舉喜，楊海峰，等.新型艉軸密封裝置的有限元分析與設計［J］.艦船電子工程，2010，30（6）：166-169.

［5］ 胡舉喜，常龍，楊海峰，等.船舶密封裝置Ω彈簧組的優化設計［J］.船舶工程，2010，32（2）：82-84.

［6］ 郭彤，李愛群，費慶國，等.零階與一階優化算法在懸索橋模型修正中的應用對比分析［J］.振動與沖擊，2007，26（4）：35-38.

［7］ More J J，Wright S J.Optimization software guide ［M］.Philadelphia：Society for Industrial&Applied Mathematics，1993.

［8］ Zheng Q，Zhuang D M.Integral global optimization algorithms，implementations and numerical tests［J］. Journal of Global Optimization，1995，7（4）：421-454.

［9］ 劉寶山，趙國忠，顧元憲.復合材料層合板結構振動聲輻射優化［J］.振動與沖擊，2008，27（12）：31-35.

［10］ 周小林，趙高暉，王國欽，等.水潤滑艉軸承負載能力的分析［J］.上海理工大學學報，2004，26（4）：378-380.

［11］ 周旭輝，楊俊.推力軸承軸向剛度對船舶軸系振動響應的影響［J］.船海工程，2012，41（4）：110-112.

（編輯：石 瑛）

Multi-parameter Optimal Design ofΩSpring Set for the Ship Seal Device

YANGMin1， LIUJian-hua1， WUTang-rong2
（1.School of Energy and Power Engineering，University of Shanghai for Science and Technology，Shanghai 200093，China；2.China Shipbuilding Industry Corporation 704 Institution，Shanghai 200031，China）

The structural compensation ability ofΩspring set，as an important component of ship seal device，directly affects the sealing effect of ship seal device.Based on zero-order optimization method，multi-parameter optimization of theΩspring set was conducted with the design variables of the characteristic thickness，width，and the radiuses of both the middle and top circles.The responses of various design parameters and the optimal solution of maximum radial stiffness were analyzed.In conclusion，the radial stiffness increases by 11.5%after the optimization.Moreover，making the harmonic response analysis ofΩspring set before and after the optimization respectively，the results verify the effectiveness ofΩspring stiffness optimization to modify its frequency compensation ability，and thus improve its structural compensation ability.

Ωspring set；structural compensation ability；zero-order algorithm；multiparameter optimization analysis；harmonic response

U 664.21文獻標示碼：A

1007-6735（2014）05-0469-04

10.13255／j.cnki.jusst.2014.05.011

2014-01-05

楊 敏（1991-），男，碩士研究生.研究方向：機械密封技術的研究和模擬.E-mail：yangminshlgdx＠163.com

柳建華（1956-），男，教授.研究方向：制冷系統節能技術與優化.E-mail：lwnlwn＿liu＠163.com