等效熱點應(yīng)力法結(jié)合臨界面法評估焊接接頭多軸疲勞強度研究
, ,
(1.中國船舶科學(xué)研究中心 船舶結(jié)構(gòu)研究室,江蘇 無錫 214082;2.大連理工大學(xué) 船舶工程學(xué)院,遼寧 大連 116024)
在船舶與海洋工程實際中,多數(shù)的焊接結(jié)構(gòu)受到復(fù)雜載荷作用而處于多軸疲勞損傷狀態(tài)。對于分析焊接部位復(fù)雜的應(yīng)力狀態(tài),熱點應(yīng)力法是目前綜合考慮評估精度和工程應(yīng)用兩個關(guān)鍵因素的最佳選擇。工程上一般采用有限元法計算焊接部位的應(yīng)力分布,并利用線性外插法來獲得熱點應(yīng)力的大小[1-2]。然而,現(xiàn)有的方法在應(yīng)用于復(fù)雜焊接結(jié)構(gòu)的多軸疲勞強度評估時,存在以下不足:①線性外插法難以用于復(fù)雜焊接接頭的熱點應(yīng)力計算。對于多軸疲勞強度評估,需要分析焊趾附近復(fù)雜應(yīng)力場的最大剪應(yīng)力、正應(yīng)力等多個應(yīng)力分量的大小和方向,而這些應(yīng)力分量的大小和方向取決于焊接部位的幾何外形和不同類型載荷的聯(lián)合作用,很難通過外插法獲得。②目前的熱點應(yīng)力法只考慮焊趾處的結(jié)構(gòu)表面應(yīng)力而忽略板厚方向應(yīng)力梯度對疲勞強度的影響,對于復(fù)雜應(yīng)力場的多軸疲勞強度評估,這種缺陷導(dǎo)致的誤差可能會更加明顯。
多軸疲勞損傷狀態(tài)下疲勞評估參考應(yīng)力第一主應(yīng)力的方向總是不斷變化,使得采用一個疲勞參量控制的疲勞理論不再適用于焊接結(jié)構(gòu)的多軸疲勞壽命預(yù)測。臨界面法認(rèn)為疲勞裂紋擴(kuò)展主要由臨界面上最大剪應(yīng)變和與其對應(yīng)的法向正應(yīng)變兩個疲勞參量控制[3]。基于臨界面法的Modified W?hler Curve Method(MWCM)方法通過對有限元計算結(jié)果進(jìn)行簡單的后處理,便可對復(fù)雜焊接結(jié)構(gòu)的多軸疲勞壽命進(jìn)行預(yù)測[4-5]。
文中提出一種新的可以應(yīng)用于復(fù)雜焊接接頭多軸疲勞強度評估的熱點應(yīng)力法,在焊趾處沿著板厚方向選取一點的結(jié)構(gòu)應(yīng)力作為疲勞強度評估的參考應(yīng)力。將該方法與基于雙參數(shù)臨界面法的MWCM法相結(jié)合,能夠有效評估復(fù)雜焊接結(jié)構(gòu)的多軸疲勞壽命。
1 等效熱點應(yīng)力的定義
熱點應(yīng)力是指最大結(jié)構(gòu)應(yīng)力或幾何應(yīng)力,作為一種參考應(yīng)力,熱點應(yīng)力只考慮結(jié)構(gòu)宏觀幾何形狀引起的應(yīng)力集中,而不考慮焊縫形狀本身所引起的局部非線性應(yīng)力的影響。
本文提出的等效熱點應(yīng)力是基于非線性應(yīng)力在板厚方向的分布處于自平衡狀態(tài)的特點。如圖1所示,處于自平衡狀態(tài)的非線性應(yīng)力必然會在靠近板材表面下的一點處應(yīng)力值變?yōu)榱悖虼嗽谠擖c處的總體應(yīng)力不包含非線性應(yīng)力,本文將這一點稱為“零點位置”。零點位置處的應(yīng)力狀態(tài)和熱點應(yīng)力的定義在本質(zhì)上是相同的,即只包含了由焊接結(jié)構(gòu)宏觀幾何尺寸引起的應(yīng)力集中,并將零點位置處的應(yīng)力稱為等效熱點應(yīng)力,作為焊接接頭疲勞強度評估的參考應(yīng)力。
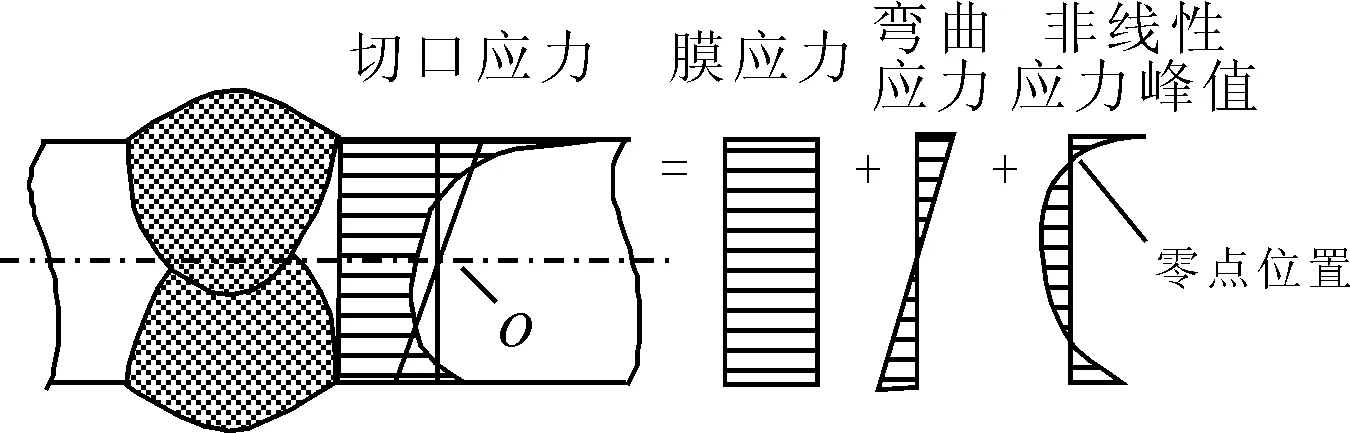
圖1 熱點處板厚方向典型的非線性應(yīng)力分布
2 零點位置分布規(guī)律
要計算一個焊接接頭的等效熱點應(yīng)力,首先要確定等效熱點應(yīng)力所在的零點位置。既然非線性應(yīng)力分布項是由焊趾本身引起的,那么零點位置必然會受到焊趾幾何外形及尺寸的影響。本文將闡明針對不同的焊趾幾何尺寸以及在不同的載荷工況下零點位置在板厚方向的分布規(guī)律。
2.1 零點位置計算
文中將對接焊縫作為研究對象,材料為普通鋼,彈性模量為210 GPa,泊松比為0.3。幾何形式見圖2,參數(shù)的選取見表1。為了便于分析,文中將零點位置全部歸一化表示為d/t。
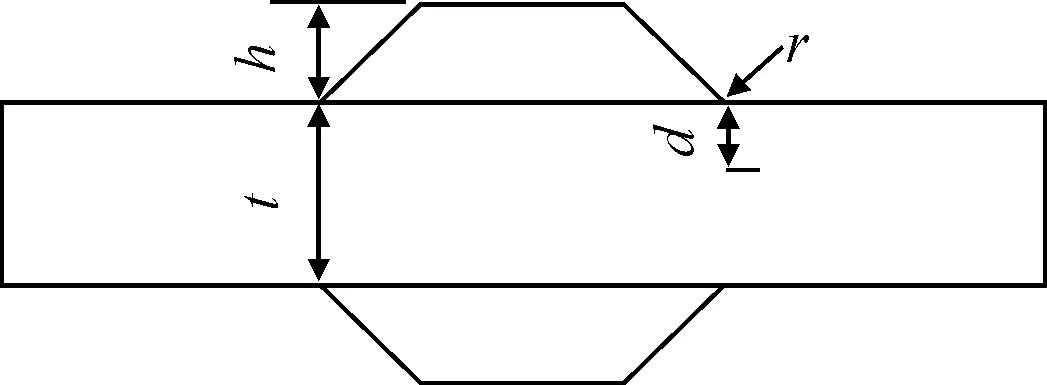
t-板厚;h-焊腿高度(間隔1 cm);d-零點位置距離平板表面深度;θ-焊趾角度(間隔5°);r-焊趾端部圓弧半徑(間隔0.5 mm)圖2 對接焊縫幾何形式

板厚t/mm焊腿高度h/mm焊趾角度θ/(°)趾端半徑r/mm209~1210~600~2
為了研究不同載荷形式對零點位置的影響,在板端施加拉伸、彎曲以及拉彎組合載荷,在平板表面處的名義應(yīng)力分別表示為σT、σB和σT+σB。定義R=σT/(σT+σB)為拉伸應(yīng)力比,表示不同的拉彎組合工況。
圖3為采用平面應(yīng)變單元建立的有限元模型,在焊趾附近網(wǎng)格尺寸設(shè)置為0.01t以保證應(yīng)力計算具有足夠的精度。
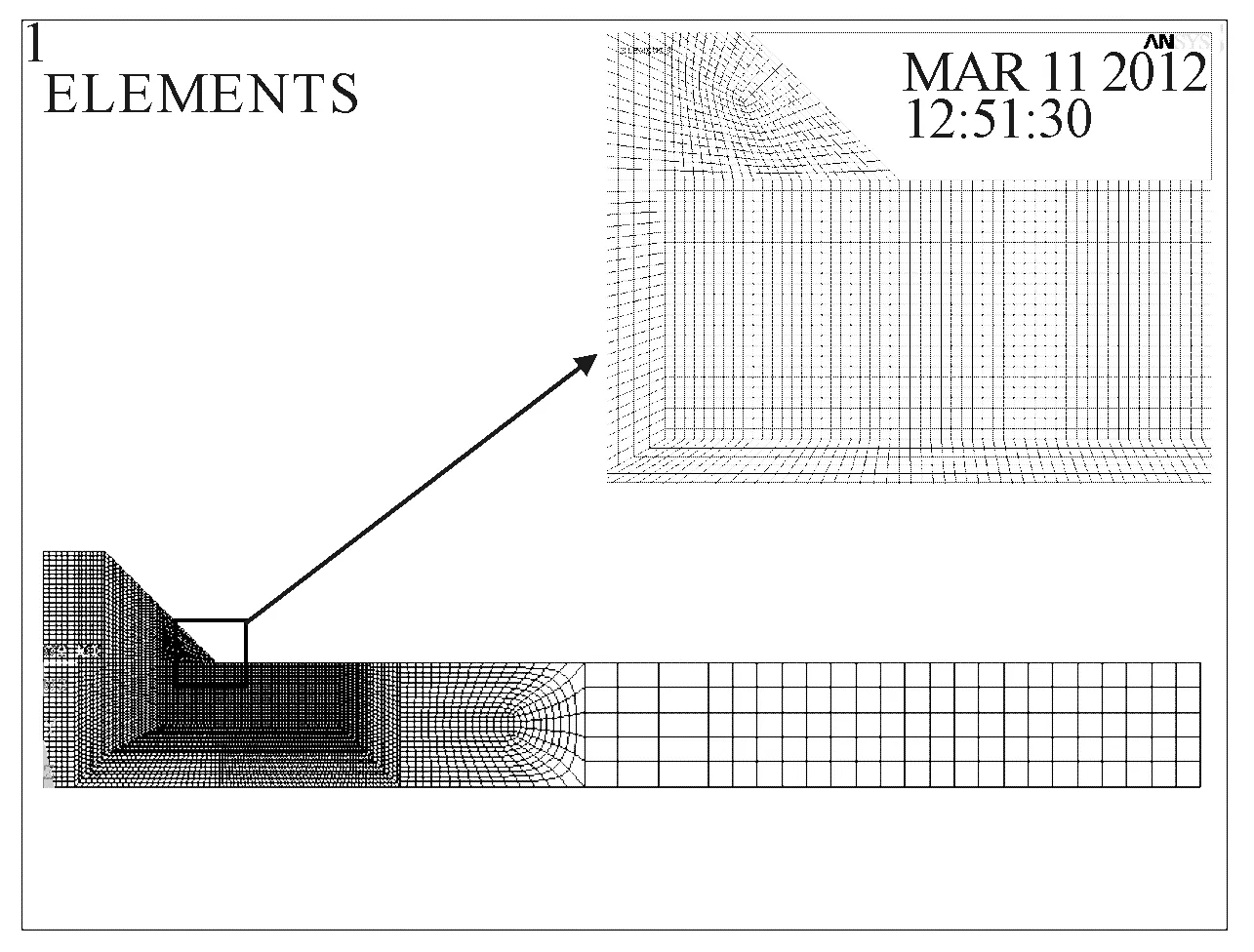
圖3 對接焊縫有限元模型
對接焊縫處的應(yīng)力集中完全是由焊趾本身引起的[6],熱點應(yīng)力集中系數(shù)為1.0,在非線性分布應(yīng)力零點位置,切口應(yīng)力將等于同樣深度的名義應(yīng)力。
圖4為某一工況下焊趾處沿板厚方向的應(yīng)力分布計算結(jié)果,其中細(xì)實線為提取每個節(jié)點第一主應(yīng)力得到的切口應(yīng)力分布曲線,細(xì)虛線為根據(jù)已知載荷工況確定的名義應(yīng)力分布曲線,兩條線的交點位置即為文中定義的零點位置。
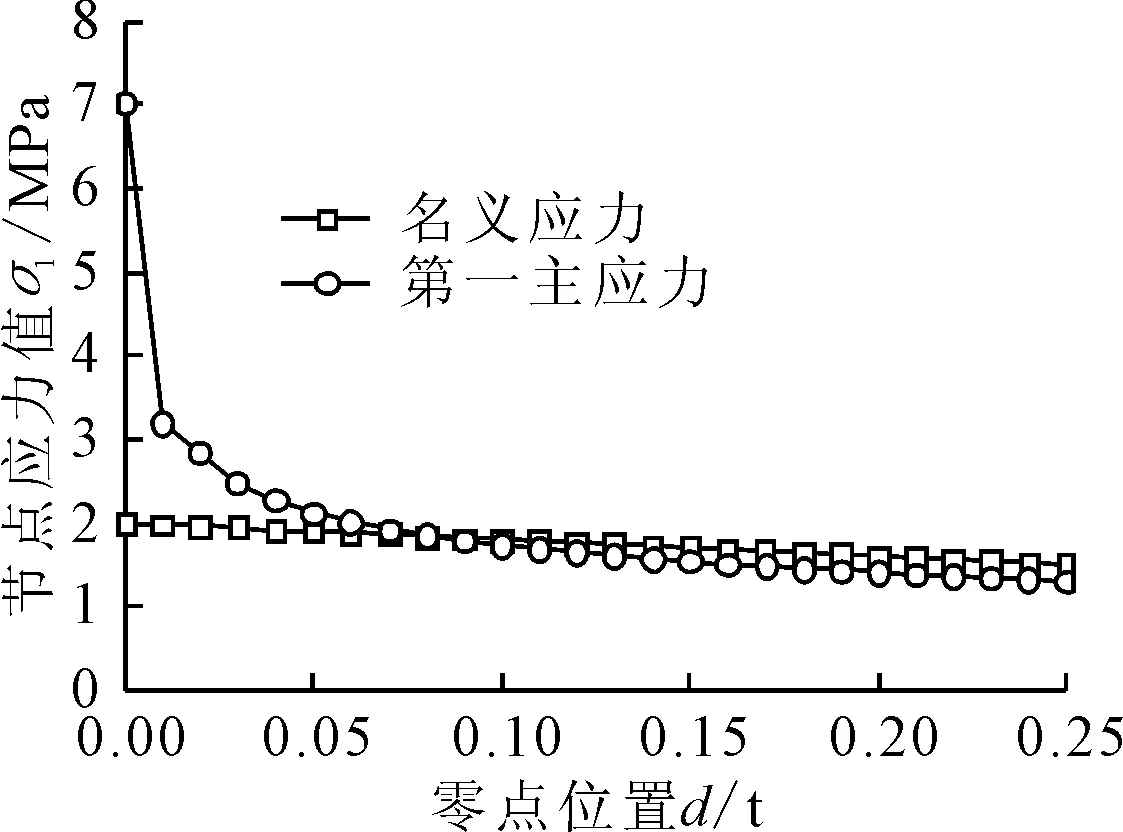
圖4 零點位置確定方法
2.2 零點位置變化趨勢
通過一系列有限元應(yīng)力計算,分別研究了在不同的載荷工況下焊縫焊腿高度(取相對高度h/t)、焊趾角度θ以及趾端半徑r的變化對零點位置的影響。圖5為固定θ=45°,r=1 mm,焊趾高度h/t從0.3增加到0.6時零點位置的變化趨勢。零點位置的所有計算結(jié)果及離散程度見圖6。
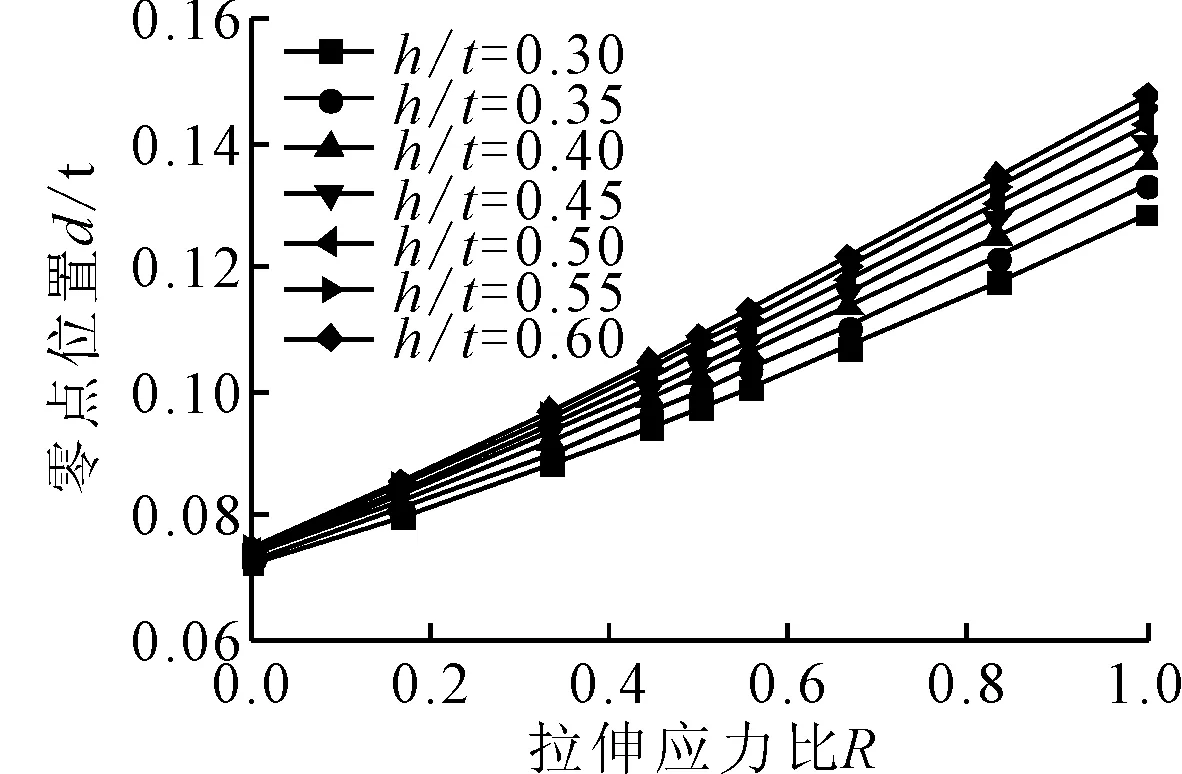
圖5 零點位置變化趨勢 (θ=45°,r=1 mm)
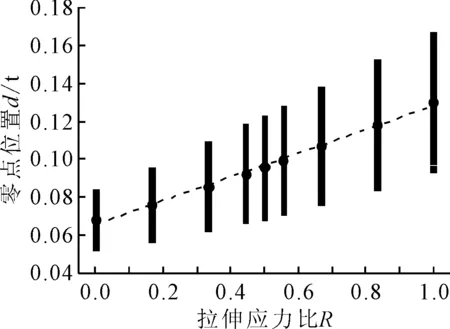
圖6 零點位置數(shù)值計算結(jié)果及線性擬合方程
由圖5可見:①不同的載荷工況對零點位置有顯著的影響,當(dāng)載荷為純彎曲時,零點位置到平板表面的距離最小。其主要原因是在純彎曲工況下焊趾處沿厚度方向的應(yīng)力梯度最大,導(dǎo)致非線性應(yīng)力峰值在很小的范圍內(nèi)下降到名義應(yīng)力的水平;而當(dāng)載荷為單向拉伸時,情況則正好相反。②在焊縫幾何尺寸完全相同的情況下,零點位置d/t與拉伸應(yīng)力比R之間存在近似的線性關(guān)系,可以用線性方程來擬合。③在同一載荷工況下,焊腿高度的增加會導(dǎo)致零點位置在一定范圍內(nèi)加深,但變化幅度不大。焊趾角度θ以及趾端半徑r的變化對零點位置的影響與焊腿高度相似。
2.3 零點位置擬合方程
有限元計算結(jié)果表明要準(zhǔn)確確定零點位置,需要建立零點位置與焊接接頭幾何尺寸以及載荷類型之間的數(shù)學(xué)關(guān)系。但是本文從工程應(yīng)用出發(fā),忽略焊接接頭幾何尺寸對零點位置的影響,只建立零點位置d/t與拉伸應(yīng)力比R之間的擬合方程。原因主要有以下兩點:
1)熱點應(yīng)力法能夠廣泛應(yīng)用于工程實際的優(yōu)點之一就是不需要考慮焊趾部位的幾何尺寸,如果本文的方法需要焊趾尺寸作為已知條件,則失去了熱點應(yīng)力法的意義。
2)計算結(jié)果表明載荷形式對零點位置的影響非常明顯,而焊趾尺寸引起的零點位置的離散程度則相對較小,而且在零點位置附近(見圖4),應(yīng)力梯度已經(jīng)變得非常平緩,即使確定的零點位置有一定的誤差,但導(dǎo)致的應(yīng)力誤差卻會相對小很多。因此,作者認(rèn)為即使完全不考慮焊趾尺寸的影響,最終的等效熱點應(yīng)力計算結(jié)果也會有較高的精度。
取每種載荷工況下零點位置最大值與最小值之間的中點進(jìn)行線性擬合,得到方程
d/t=0.062R+0.066
(1)
式(1)表示在同一載荷工況下,任何幾何尺寸的焊接接頭將采用同一個零點位置d/t。利用擬合的零點位置獲得的等效熱點應(yīng)力記為σfitting,在真實的零點位置獲得的等效熱點應(yīng)力記為σreal,兩者之間的誤差表示為
(2)
與圖6中的算例對應(yīng),利用擬合方程獲得的等效熱點應(yīng)力的計算誤差見圖7。
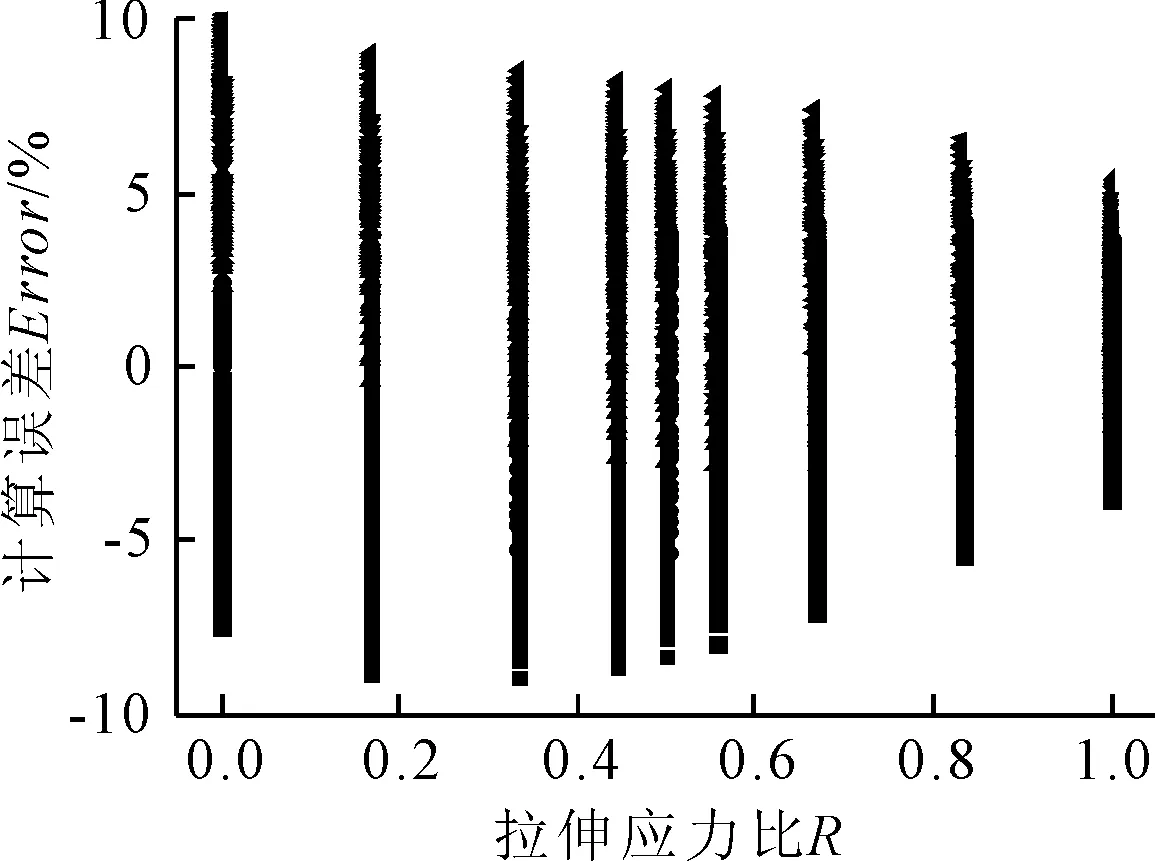
圖7 等效熱點應(yīng)力的計算誤差
在以彎曲為主的載荷工況下,由于板厚方向的應(yīng)力梯度較大,導(dǎo)致等效熱點應(yīng)力的計算誤差也較大,但最大誤差不超過10%;在以拉伸為主的載荷工況下,最大誤差則可降到5%左右。
3 等效熱點應(yīng)力法的精度驗證
為了驗證等效熱點應(yīng)力法的精度,選擇一組DNV船級社采用的焊接試件進(jìn)行分析[7],試件的具體幾何尺寸見DNV規(guī)范[8]。選擇試件1和4分別代表以拉伸和彎曲為主的載荷工況進(jìn)行有限元分析。①根據(jù)現(xiàn)有的熱點應(yīng)力計算方法,采用20節(jié)點塊體單元,設(shè)置網(wǎng)格大小為t×t,分別在距離焊趾0.5 t和1.5 t處讀取單元應(yīng)力,利用線性外插法計算熱點應(yīng)力;②采用文中的方法計算等效熱點應(yīng)力,選擇8節(jié)點塊體單元,設(shè)置零點位置附近的網(wǎng)格大小為0.05 t×0.05 t,兩個試件的有限元模型見圖8~9。
圖8 焊接試件1有限元模型
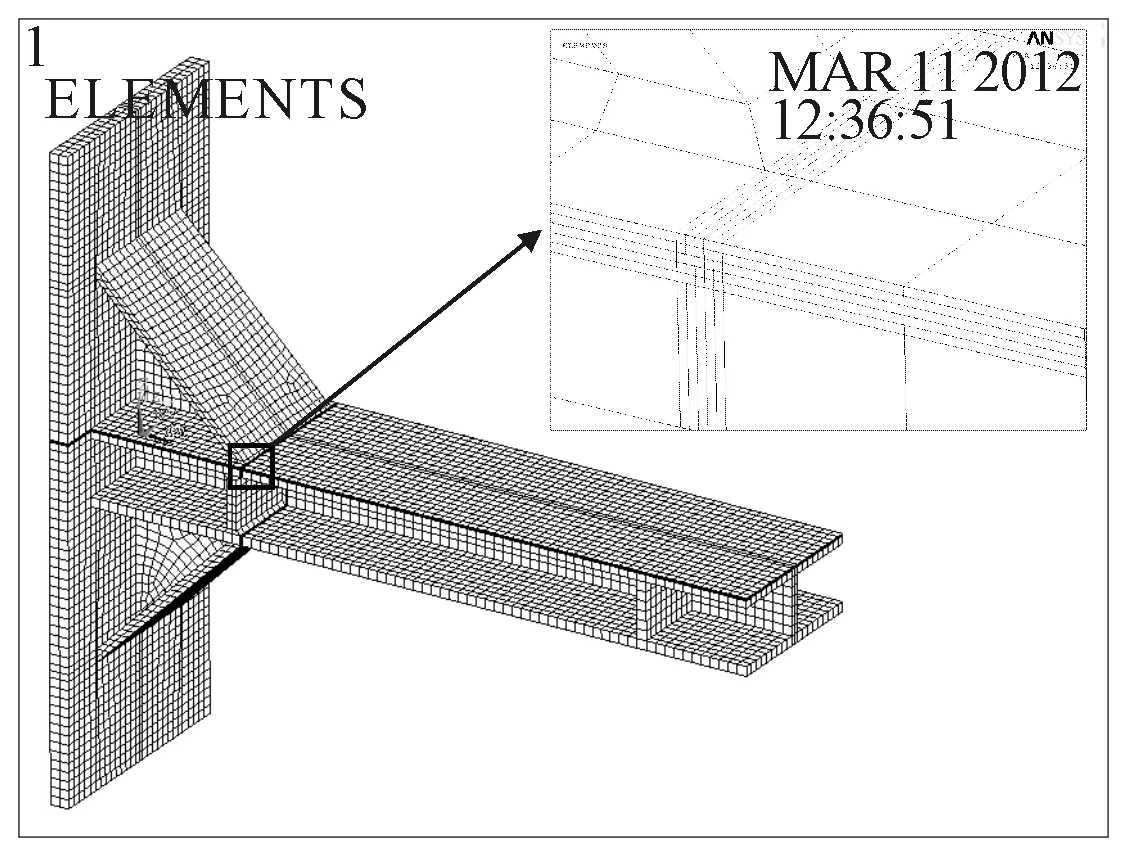
圖9 焊接試件4有限元模型
兩種方法熱點應(yīng)力集中系數(shù)計算結(jié)果見表2。
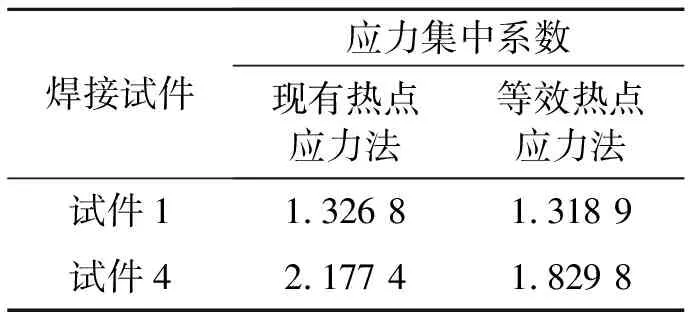
表2 熱點應(yīng)力集中系數(shù)計算結(jié)果
試件1主要承受拉伸應(yīng)力,兩種方法的計算結(jié)果非常接近,說明等效熱點應(yīng)力和線性插值法計算的熱點應(yīng)力在厚度效應(yīng)不明顯的情況下具有很好的一致性。試件4主要承受彎曲應(yīng)力,等效熱點應(yīng)力要明顯小于線性插值法計算的熱點應(yīng)力,和試驗結(jié)果更加接近。
圖10為該組焊接試件疲勞試驗的結(jié)果,其中縱坐標(biāo)為采用線性外插法獲得的熱點應(yīng)力。根據(jù)等效熱點應(yīng)力法和現(xiàn)有熱點應(yīng)力法計算結(jié)果的比例關(guān)系,對原有的試驗數(shù)據(jù)進(jìn)行修正。如圖11所示,修正后的試驗數(shù)據(jù)離散程度明顯降低,說明文中提出的等效熱點應(yīng)力能夠在一定程度上考慮厚度效應(yīng)的影響,具有更高的計算精度。
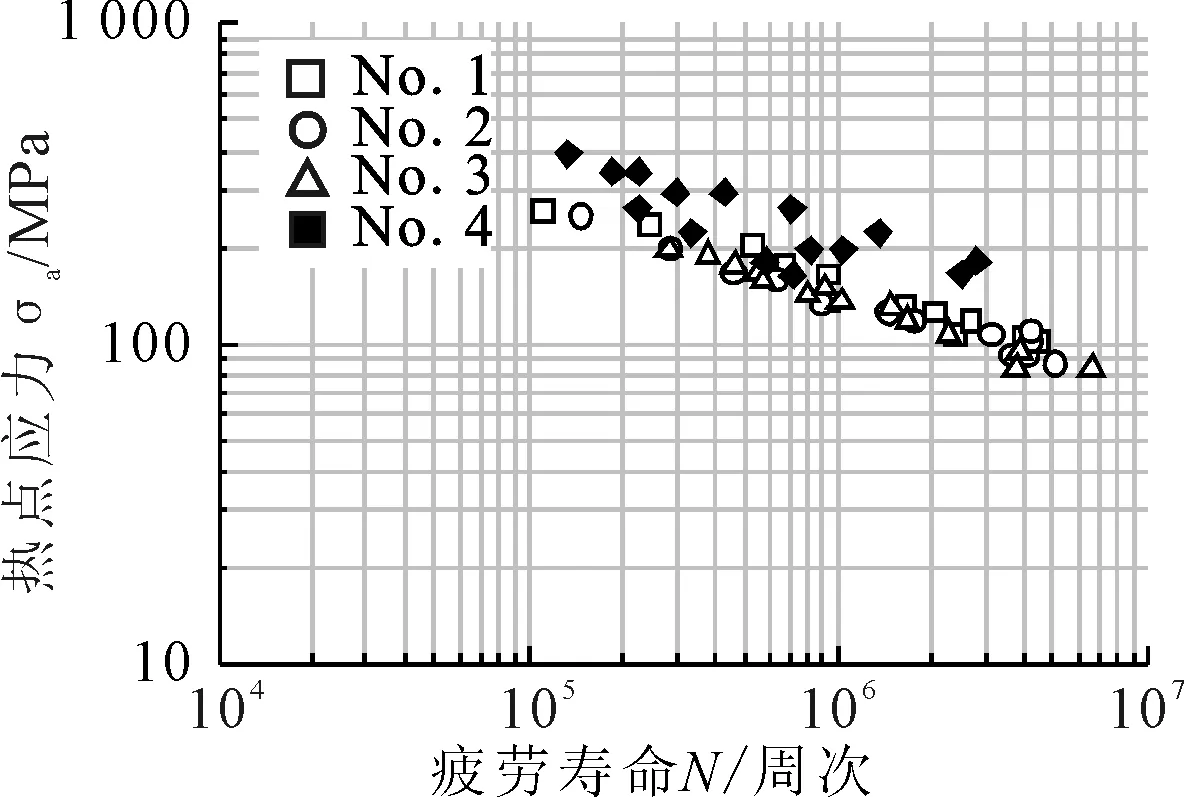
圖10 DNV焊接試件疲勞試驗數(shù)據(jù)

圖11 修正為等效熱點應(yīng)力表示的疲勞試驗數(shù)據(jù)
4 多軸疲勞強度評估
4.1 基于臨界面法的MWCM法
MWCM法認(rèn)為結(jié)構(gòu)的最大剪應(yīng)力幅值面為疲勞臨界面,為疲勞裂紋萌生概率最大的平面。疲勞裂紋在最大剪應(yīng)力面處萌生,而最大剪應(yīng)力面上的法向正應(yīng)力有助于疲勞裂紋的擴(kuò)展。因此,MWCM法采用最大剪應(yīng)力幅值Δτ和法向正應(yīng)力幅值Δσn作為評估焊接結(jié)構(gòu)多軸疲勞壽命的疲勞損傷參量,可用它們的比值ρw=Δτ/Δσn表示焊接結(jié)構(gòu)所受的復(fù)雜應(yīng)力狀態(tài)。見圖12。
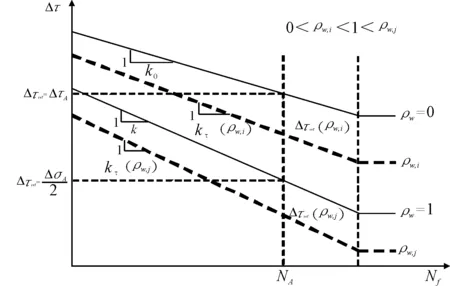
圖12 Modified W?hler曲線
由圖12可見,任何一條Modified W?hler曲線均可以通過反向斜率和參考失效次數(shù)下的參考剪應(yīng)力范圍惟一確定。L.Susmel等人定義控制方程如下。
kτ(ρw)=-2ρw+5 (0≤ρw≤1)
kτ(ρw)=3 (ρw≥1)
(3)
Δτref(ρw)=-32ρw+96 (0≤ρw≤2)
Δτref(ρw)=32 (ρw≥2)
(4)
MWCM法不依賴于焊接結(jié)構(gòu)所承受外界載荷的復(fù)雜性,其評估的多軸疲勞損傷僅與疲勞臨界點處比值ρw有關(guān),給定應(yīng)力水平下焊接結(jié)構(gòu)的多軸疲勞循環(huán)次數(shù)見式(5),一般取NA=5×106次。
(5)
4.2 等效熱點應(yīng)力法結(jié)合MWCM法預(yù)測多軸疲勞強度
對于Model4焊接試件,采用solid45單元,有限元模型見圖9,焊趾端部沿x方向和沿厚度方向網(wǎng)格大小為0.05t,其他區(qū)域網(wǎng)格最大為t×t,邊界條件為端面固定約束。
在水平桁材加強筋處施加垂直向下的集中載荷為
fz=128sinθ
(6)
在最右端施加水平向右的集中載荷為
(7)
結(jié)構(gòu)疲勞臨界面由于結(jié)構(gòu)承受多軸非比例載荷的作用而不斷發(fā)生變化,使得疲勞控制參量的大小和方向也是不斷變化的,為了更準(zhǔn)確地反映非比例載荷作用下的應(yīng)力狀態(tài),將非比例載荷離散為36個載荷離散點,計算每一個載荷離散點的最大剪應(yīng)力和對應(yīng)的法向正應(yīng)力。
對于每一個載荷點,可以計算得到該工況下的拉伸應(yīng)力比、零點位置、零點位置處最大剪應(yīng)力以及其對應(yīng)的法向正應(yīng)力,見圖13~16。
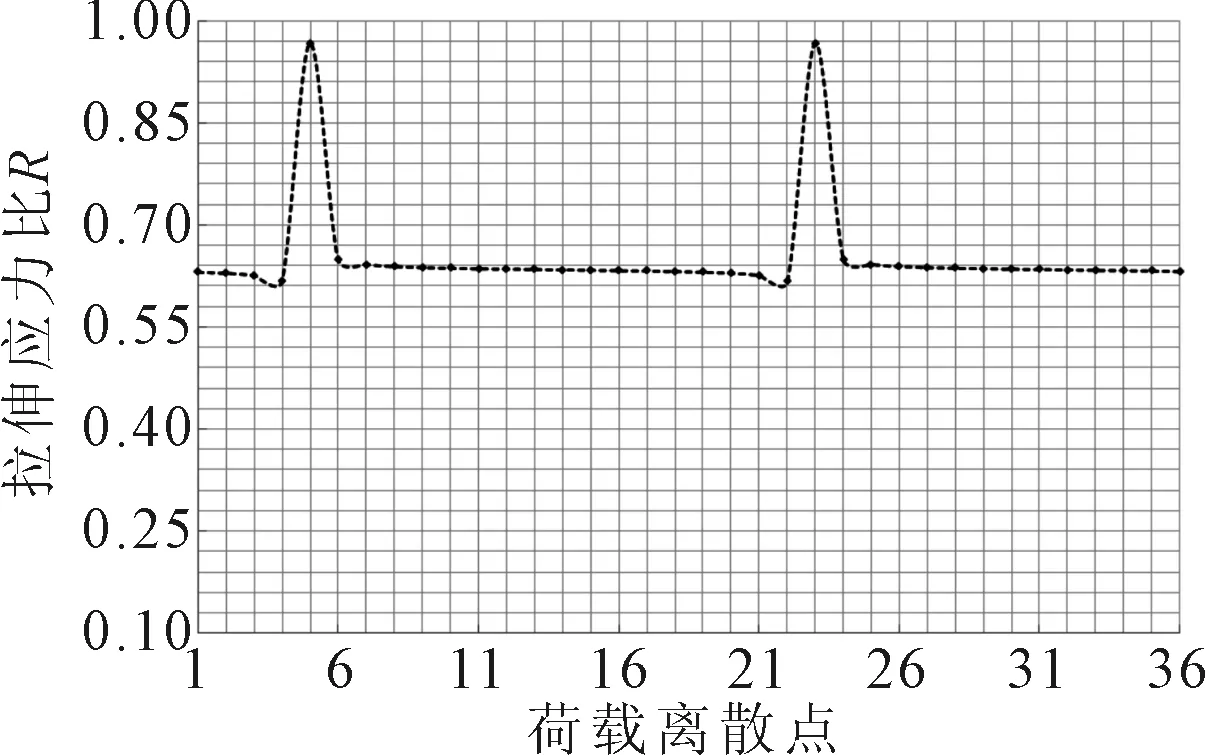
圖13 拉伸應(yīng)力比R匯總
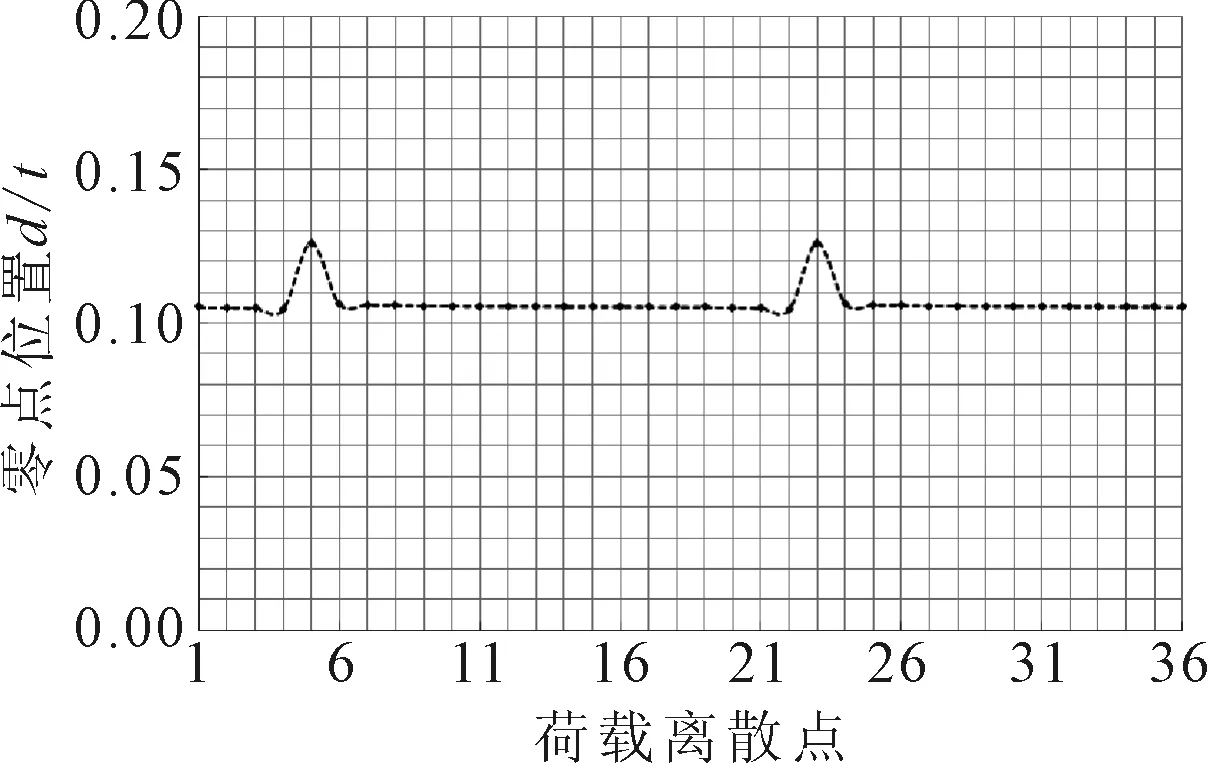
圖14 零點位置匯總
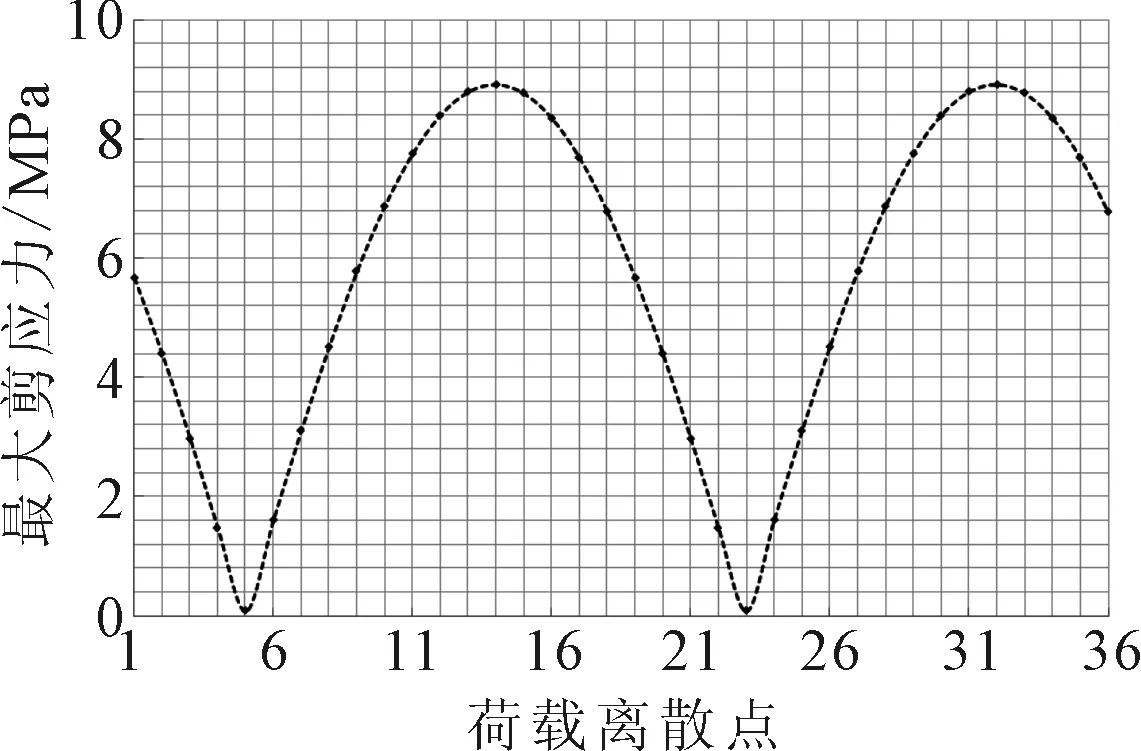
圖15 最大剪應(yīng)力匯總
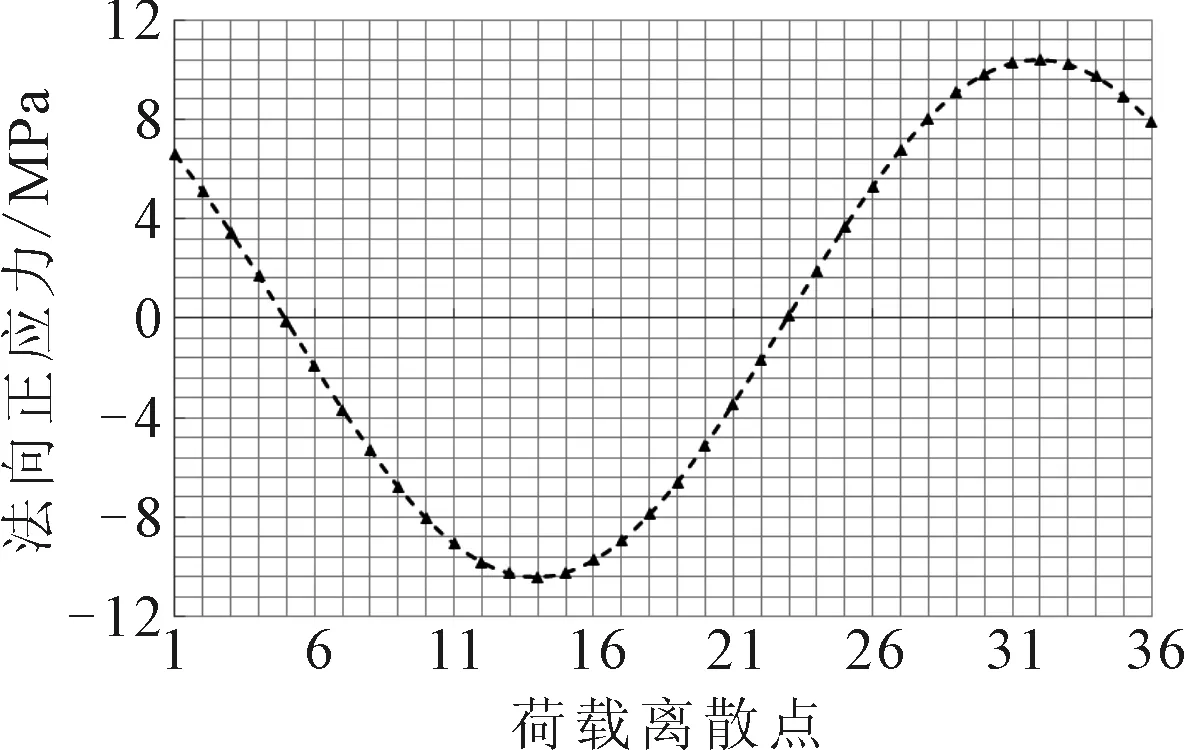
圖16 法向正應(yīng)力匯總
由圖15和圖16可以計算得到最大剪應(yīng)力幅值Δτ、法向正應(yīng)力幅值Δσn以及它們的比值ρw,通過控制方程計算反向斜率和參考剪應(yīng)力范圍,繪制Modified W?hler曲線如圖17,根據(jù)式(5)便可計算得到焊接結(jié)構(gòu)在一定載荷路徑給定應(yīng)力水平下的多軸疲勞壽命。

圖17 Modified W?hler曲線
5 結(jié)論
1)焊接接頭零點位置受到焊趾本身幾何尺寸以及載荷形式的影響,但是從工程應(yīng)用出發(fā),可以完全忽略焊趾尺寸的影響,引起的等效熱點應(yīng)力計算誤差不超過10%,建立的零點位置擬合方程只和載荷形式相關(guān)。
2)在以拉伸為主的載荷工況下,等效熱點應(yīng)力和線性外插法計算的熱點應(yīng)力非常接近,說明兩種方法具有很好的一致性;在以彎曲為主的載荷工況下,等效熱點應(yīng)力法能夠在一定程度上考慮厚度效應(yīng)對疲勞強度的影響,比原有的熱點應(yīng)力法具有更高的精度。
3)等效熱點應(yīng)力法能夠直接分析某一點的復(fù)雜應(yīng)力狀態(tài),和基于臨界面法的MWCM法相結(jié)合,建立了一種更加精確的復(fù)雜焊接接頭多軸疲勞強度評估方法。
[1] 張 毅,黃小平,崔維成,等.對接接頭焊趾應(yīng)力集中有限元分析[J].船舶力學(xué),2004,8(5):91-99.
[2] 王甲畏,王德禹.基于熱點應(yīng)力的FPSO焊接結(jié)構(gòu)疲勞問題研究[J].船舶工程,2005,27(1):62-66.
[3] BROWN M W,MILLER K J.A theory for fatigue failure under multiaxial stress and strain conditions.Proc.Inst[J].Mechanical Engineers,1973,187:745-755.
[4] SUSMEL L,LAZZARIN P.A bi-parametric W?hler curve for high cycle multiaxial fatigue assessment[J].Blackwell Science Ltd.Fatigue Fract Engng Mater Struct,2001(25):63-78.
[5] SUSMEL L.A novel engineering procedure to predict the lifetime of steel welded joints subjected to both uniaxial and multiaxial fatigue loading[J].International Journal of Fatigue,2008,30:888-907.
[6] MADDOX S J.Hot-spot stress design curves for fatigue
assessment of welded structures[J].International Journal of Offshore and Polar Engineering,2002,12(2):134-141.
[7] LOTSBERG I,SIGURDSSON G.Hot spot stressS-Ncurve for fatigue analysis of plated structures[J].Trans-actions of the ASME,2006,128:330-336.
[8] DNV-RP-C203. Fatigue strength analysis of offshore steel structures:Appendix D Commentary[S].Oslo:Det Norske Veritas,2005.

