導邊形狀對軸流式噴泵性能影響的計算分析
,,,
(海軍工程大學 動力工程學院,武漢 430033)
噴水推進在高速高性能船舶領域得到廣泛應用[1-3]。噴水推進器主要由噴水推進泵(以下稱為噴泵)和進水流道兩部分構成。噴泵是噴水推進核心部件,噴泵對效率、揚程、流量、抗空化等方面有較高要求,設計難度較大[4-5]。近年來,計算機技術和計算流體力學(computational fluid dynamics,CFD)發展很快,與傳統水力模型試驗相比,其周期短,耗資較少,CFD在船舶噴水推進技術研發、預報、設計中的應用日趨廣泛。在以前葉片進口邊位置和形狀主要憑經驗來設計,對性能曲線的影響只有試驗后才知曉[6]。在理論上,通過泵氣蝕余量公式,認為修圓葉片進口外圓部分可以提高葉片的抗汽蝕性能[7]。楊軍虎等[8]利用CFD軟件FLUENT對低轉速軸流泵進行過葉片外緣修圓對性能的影響進行過研究,重點對葉頂間隙的流場進行了分析。國外Angelo Cervone、Giovanni Pace等利用水力試驗,研究發現導邊幾何形狀對空化特性影響較大。對于高轉速軸流式噴水推進泵,空化是非常重要的考慮因素,葉片導邊形狀對該空化性能和水力性能之間的影響研究報道仍比較少。為了研究導邊形狀對水力效率和空化性能的影響情況,文中運用CFD方法,通過改變某高速摩托艇噴水推進泵導邊形狀,研究導邊形狀對該類噴水推進泵敞水效率和空化性能的影響,為高轉速泵的設計、性能優化提供基本參考。
1 控制方程與湍流模型
1.1 控制方程
流體流動須遵守質量守恒規律,動量守恒定律和能量守恒定律。控制方程即為這些守恒定律的數學描述,包括連續性方程和動量方程(也稱Navier-Stokes方程,簡稱N-S方程)。在定常條件下,選用不可壓縮的三維連續方程和RANS方程模擬噴水推進泵內流場。
1)質量守恒方程。
▽·(ρV)=0
(1)
2)動量守恒方程(N-S方程)。
(2)
3)能量守恒方程。
(3)
1.2 湍流模型
利用有限體積法對RANS偏微分方程進行離散,進而對其進行數值求解。所有算例都采用SST(shear stress transport)模型來封閉方程組。SST模型結合了κ-ε模型和κ-ω模型的優點, 在近壁面區域,采用κ-ω模型模擬,湍流耗散較小,收斂性好。在湍流充分發展區域,采用κ-ε模型,計算效率高,對復雜流場的適應性更好。兩種模型的結合能夠較好地模擬粘性底層的流動[9]。SST模型的最大優點就在于考慮了湍流剪切應力,從而不會對渦流黏度造成過度預測[10]。研究采用高階SST模型。
1.3 CFD方法驗證
在對該高速摩托艇軸流式噴泵進行CFD計算前,先以KaMeWa71SⅡ型噴水推進器的混流式噴水推進泵為例對其水動力特性進行數值模擬,并與廠商提供的噴水推進器數據進行比較,以驗證所用方法和模型的可信性。
KaMeWa71SII型噴水推進器的混流式噴水推進泵幾何模型見圖1。

圖1 KaMeWa71SII幾何模型
該噴泵葉輪進口直管處直徑為710 mm,葉輪有6片,導葉11片。該噴泵流體性能數值計算的幾何分為噴口、導葉、葉輪以及本文為計算敞水性能所添加的進口直管。噴口和進口直管都用ICEM軟件,劃分六面體網格。導葉部和葉輪部用TurboGrid軟件劃分六面體網格,對葉輪進行網格無關性計算,計算結果見圖2。
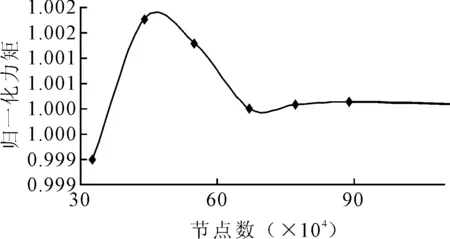
圖2 網格無關性計算
經計算葉輪網格至少需要70萬,本研究該葉輪網格實取98.3萬。其他部件的網格數見表1。
邊界條件為總壓進口,靜壓出口。時間步按CFX推薦設置,設為物理時間1/ω(ω為轉速,(°)/s)。
噴水推進泵軸功率計算結果見表2。由表2可見,計算值與廠商提供數據相對誤差均在1.5%以內,滿足工程要求。故從工程應用的角度來看,該方法計算水動力特性是可信的。
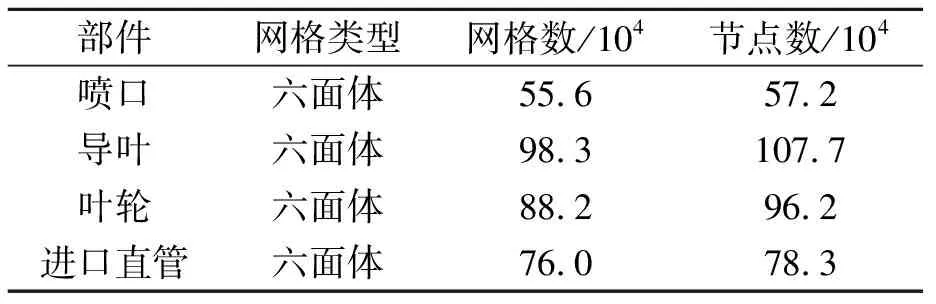
表1 各部分網格數
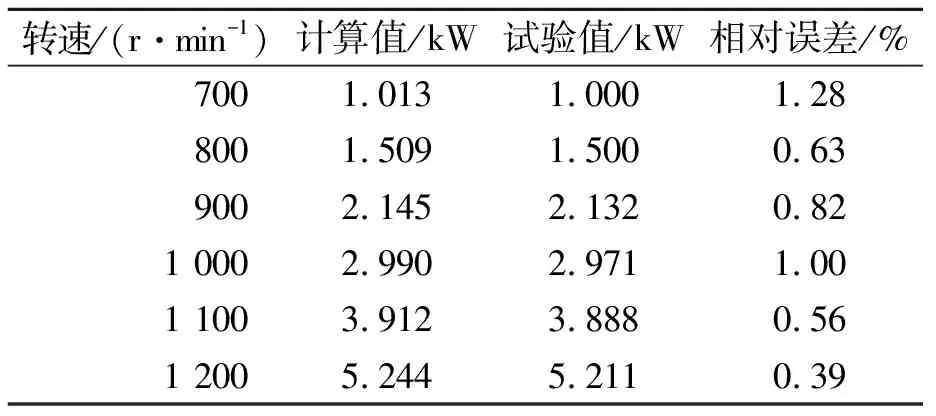
表2 CFD計算值與試驗值對比
2 CFD模擬計算
研究對象為某高速摩托艇噴水推進器的噴水推進泵,其轉速較高,額定轉速為7 500 r/min。僅以該軸流式泵體的敞水性能為研究對象。該噴水推進泵為單級軸流泵,通過改變導邊的修圓情況,研究導邊對該泵性能的影響。
2.1 幾何建模
根據摩托艇噴水推進器幾何,利用CAD三維建模軟件UG進行幾何建模。噴泵分為葉輪體、導葉體和噴口段3部分。噴泵葉輪葉片為3片,導葉為6片,噴口段也對應設置了6片二級導葉以加強整流效果。該軸流式噴泵尺寸較小,葉輪直徑為155.5 mm,葉頂間隙為0.5 mm。導葉體和噴口段幾何模型見圖3,網格劃分見圖4。
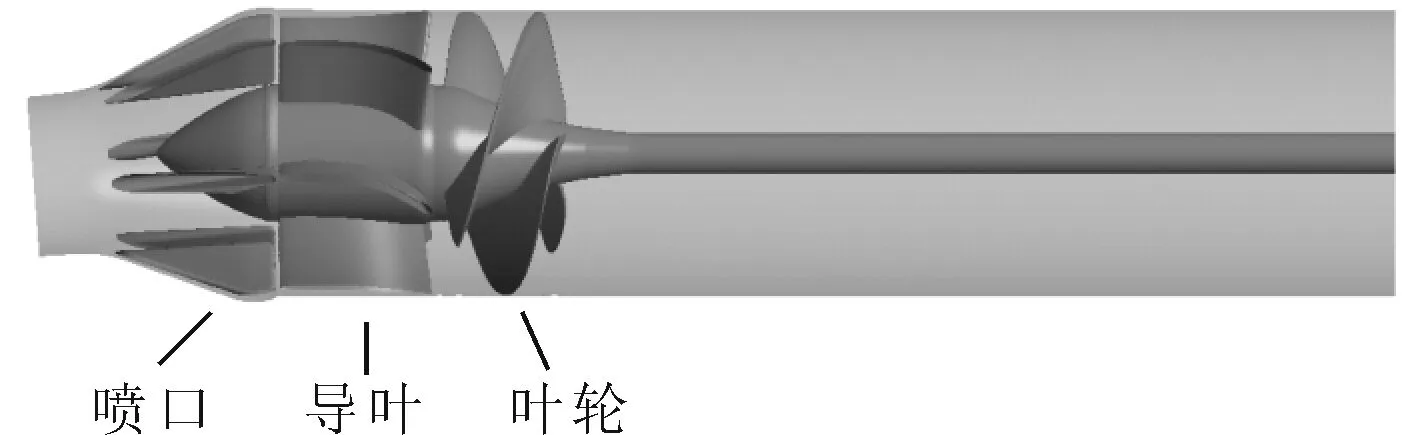
圖3 噴水推進泵幾何模型

圖4 噴水推進泵網格
對于該噴泵葉輪的建模分為修圓導邊幾何與未修圓導邊的幾何。原噴泵幾何為葉輪a。葉輪a較未修圓幾何葉片(以下稱為葉輪c)在導邊形狀上有較大改變,導邊形狀為“c”字形。葉輪b修圓程度介于葉輪a、c之間,見圖5。
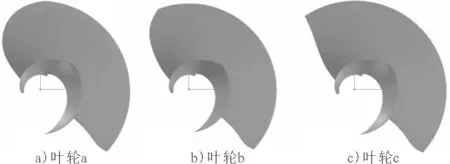
圖5 葉輪a、葉輪b、葉輪c單通道幾何
2.2 網格劃分
葉輪和導葉用ANSYS 12.0軟件中專為旋轉機械劃分網格的CFX-TurboGrid軟件。由于葉輪扭曲程度較大,故采用J型拓撲,導葉采用H型拓撲結構。噴口由于包含了二級導葉,幾何較為復雜,用ICEM軟件,四面體網格進行劃分,在壁面邊界用菱柱形網格進行加密,對細小部件用密度盒加密,確保對幾何描述的準確性。在對葉輪葉片網格無關性分析中,通過對葉輪a單通道網格節點數設定變化,對計算的軸力矩進行監測,力矩變化波動見圖6。
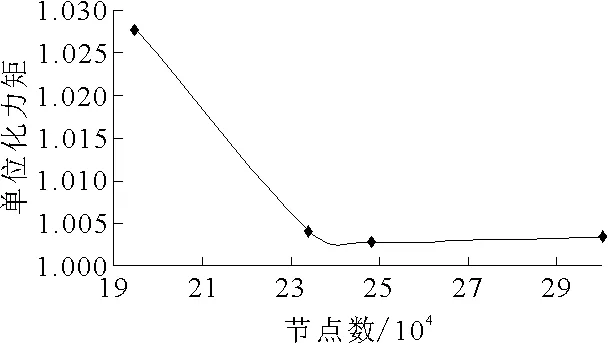
圖6 網格無關性計算
經計算葉輪總網格至少需70.8萬節點,本研究實取80.5萬以上。其他部分取較大的網格數以保證網格滿足要求。具體網格數和節點數見表3。
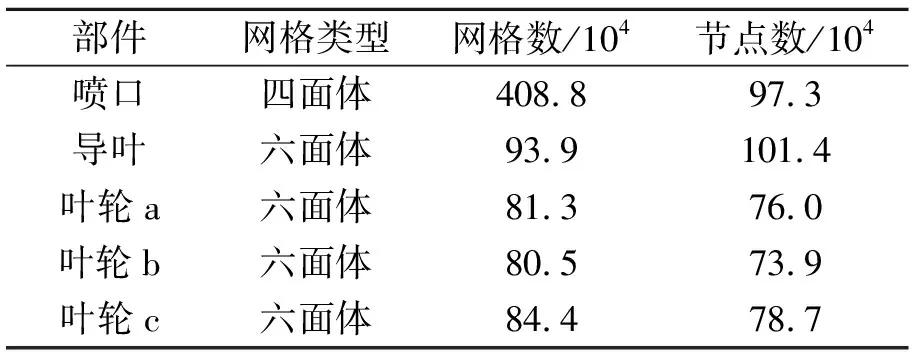
表3 具體網格數和節點數
2.3 邊界條件設置
對噴泵敞水性能進行計算時,為保證均勻流動,在葉輪進口前加直管進流道,管徑與葉輪進口直徑相等,長度在2倍直徑以上。采用邊界條件為流量進口,靜壓出口邊界條件,葉輪葉片與輪轂為相對靜止壁面條件,泵殼設為絕對靜止壁面條件。在計算空化性能時,在原有基礎上加入空化模型進行計算。
3 計算結果分析
噴泵的敞水性能指孤立泵在均勻進流條件下的性能,即不加進水流道的水力性能。模擬計算噴泵在7 500 r/min的情況下,噴泵葉輪分別采用葉輪a、b和c計算流量190~230 kg/s的軸功率、揚程和效率,見圖7~9。
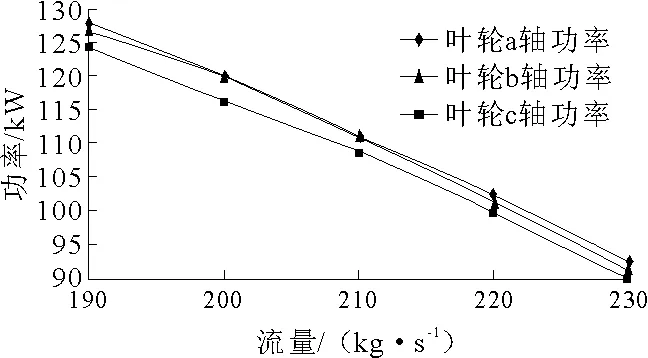
圖7 軸功率對比
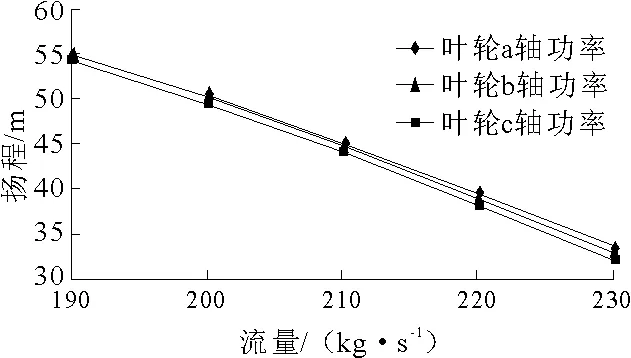
圖8 揚程對比
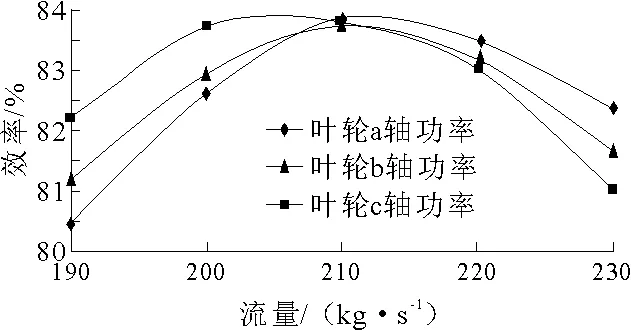
圖9 效率對比
分析發現,葉輪a、b和c的功率和揚程都有微小變化。葉輪a的功率最大,葉輪c的功率最小。因為該軸流式噴泵的葉片包角較大,修圓導邊后造成葉片做功面積減小,但進流角相對于葉輪c會變大,在這兩種作用的綜合作用下,造成該泵的功率在葉輪a的情況下所需功率最大。
分析還發現修圓導邊對該裸泵的工作點效率影響微小,但在小于工況點的流量時,效率明顯低于未修圓導邊。分析認為葉輪外緣修圓后,泄漏流動加強,降低了做功效率。
為進一步計算導邊形狀對空化性能的影響,在原計算模型的基礎上加入空化模型,分析葉片在最高效率工況點,流量為210 kg/s時的空化情況見圖10。
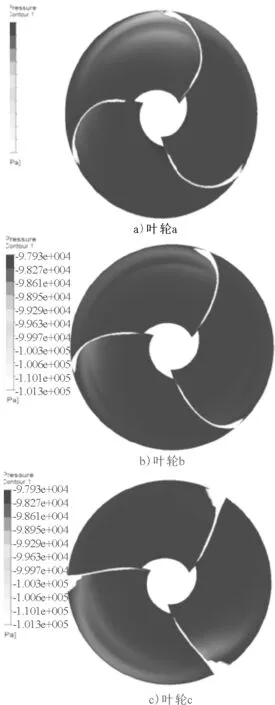
圖10 空化對比
從空化的對比圖中可以發現,葉片空化都發生在葉稍和導邊部分,葉輪c的空化面積明顯最多,葉輪a空化面積最小,這與用理論分析的情況一致。一方面,流進葉輪的液體先與導邊中部接觸,獲得能量后一部分液體沿著導邊向葉稍方向流動,旋轉能量增加了,壓力也增加了,延遲了空化的發生;另一方面通過后處理葉輪的流場矢量,可以發現在葉稍處流動非常劇烈,葉輪a的弧形導邊相對于葉輪c的直線導邊可以明顯地減少來流的沖擊,削弱了二次流的影響,見圖11。
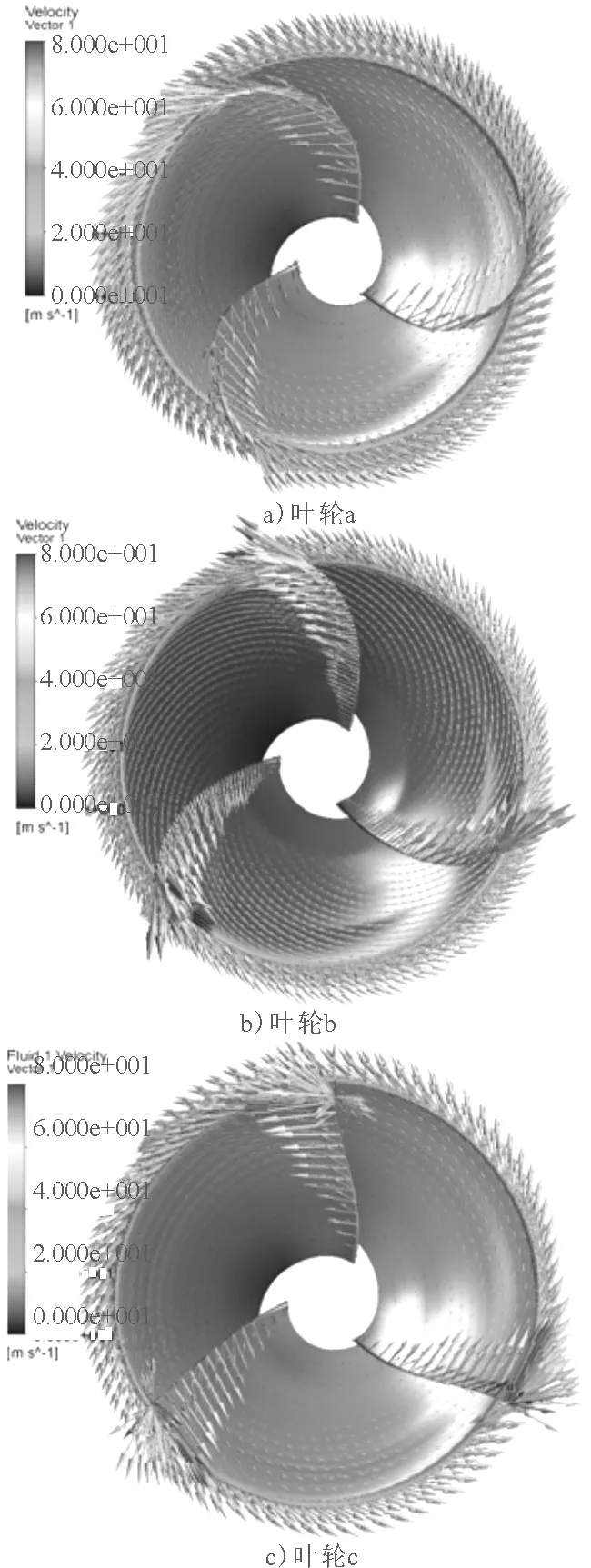
圖11 葉輪流場矢量
葉頂部分是做功和流動最強烈的地方,葉片外緣導邊部分修圓以后,造成葉片葉稍卸載,減小了空化發生面積。
4 結論
1)對于高轉速的軸流泵,修圓導邊的葉片對軸流泵的功率和揚程有微小的影響,會造成小于工作點流量時的效率降低;
2)修圓導邊的葉片在空化性能上優于直導邊的葉片,空化面積明顯減少,有利于葉片葉稍卸載。
[1] BULTEN N.Numerical analysis of a waterjet propulsion system[D]. Eindhoven, The Netherlans:The Eindhoven University of Technology,2006.
[2] 劉承江,王永生,丁江明等.現代噴水推進裝置的演變[J].艦船科學技術,2006,28(4):8-12.
[3] ALLISON J L.Marine waterjet propulsion[J].Transaction of SNAME,1993,101:275-335.
[4] ALLISON J L,JIANG C B.Modern tools for waterjet pump design and recent advances in the field[C]∥Internationa Conference on Waterjet Propulsion Ⅱ.RINA,Amsterdam,1998:128-142.
[5] 湯方平.噴水推進軸流泵設計及紊流數值分析[D].上海:上海交通大學,2006.
[6] 李世煌.葉片泵的非設計工況及其優化設計[M].北京:機械工業出版社,2006.
[7] 關醒凡.軸流泵和斜流泵[M].北京:中國宇航出版社,2009.
[8] 楊軍虎,馬靜先,張人會,等.軸流泵葉片外緣修圓對泵性能的影響[J].蘭州理工大學學報,2007,33(5):60-63.
[9] 靳栓寶.基于CFD噴水推進泵性能分析及優化設計[J].船海工程,2010,39(2):125-129.
[10] 謝龍漢,趙新宇,張炯明.ANSYS CFX流體分析及仿真[M].北京:電子工業出版社,2012.

