雙列圓錐滾子軸承功耗特性研究

鄧四二,胡廣存,董曉

(1.河南科技大學機電工程學院,河南洛陽 471003;2.浙江兆豐機電股份有限公司,浙江杭州 311232)

雙列圓錐滾子軸承功耗特性研究

鄧四二1,2,胡廣存1,董曉1

(1.河南科技大學機電工程學院,河南洛陽 471003;2.浙江兆豐機電股份有限公司,浙江杭州 311232)

在滾動軸承動力學理論基礎上,建立了雙列圓錐滾子軸承非線性動力學微分方程及其摩擦功耗數學模型,采用精細積分法和預估-校正Adams-Bashforth-Moulton多步法相結合的方法進行求解,分析了軸承不同工況參數、結構參數及工藝參數對軸承摩擦功耗的影響。研究結果表明:軸承摩擦功耗隨傾覆力矩及轉速的增加先緩慢增加然后近似線性增加,轉速對軸承摩擦功耗的影響比較明顯,在滿足使用要求下應盡量選取低轉速;側向載荷比的增加使“壓緊側”軸承摩擦功耗增加,“放松側”減小,兩側摩擦功耗差值增加;軸承摩擦功耗隨大擋邊傾角的增加而增加,隨滾子球基面半徑的增加而減小;滾子波紋度為奇數階次時,軸承摩擦功耗隨波紋度幅值的增加呈先升高后降低的趨勢;偶數階次時,軸承摩擦功耗隨波紋度幅值的增加而增加。

機械學;軸承動力學;雙列圓錐滾子軸承;功耗

0 引言

雙列圓錐滾子軸承作為裝甲車輪轂單元的關鍵部件,其摩擦功耗等性能直接影響到整車的安全性、使用壽命和舒適度。雙列圓錐滾子軸承工作時,既能承受較大的徑向載荷,又能承受一定的軸向載荷和傾覆力矩,受力情況比較復雜,對其動態性能分析較為困難。

20世紀70年代,Gupta[1-2]建立了滾動軸承動力學分析模型ADORE,但模型中對圓錐滾子軸承保持架結構進行了簡化,不能真實地反映滾子在保持架兜孔內的動態性能。文獻[3-4]利用數值計算方法對雙列圓錐滾子軸承動力學微分方程進行求解,提出了DRTRB綜合模型,研究了軸承在非Newton流變模型下的拖動等性能。Choi等[5]采用遺傳算法對汽車輪轂軸承進行分析研究,通過改變離散設計變量對輪轂軸承進行了優化設計。國內學者黎桂華等[6]基于轎車線性剛體運動的穩態轉彎模型對輪轂軸承外部載荷進行推導計算,分析了軸承外部載荷特性。陳雪峰[7]對汽車輪轂軸承進行疲勞分析,通過汽車輪轂軸承組件設計及潤滑系統的客觀分析對軸承疲勞失效成因進行詳細闡述,進而預防輪轂軸承的疲勞失效。武福等[8]以動車組動力轉向架的軸箱軸承(密封雙列圓錐滾子軸承)為研究對象,利用溫度場和熱應力場的耦合關系,建立軸承的數值分析模型,但是模型中沒有考慮軸承自轉和所受軸向載荷的影響。

目前,國內外對輪轂用圓錐滾子軸承的研究大多以單列圓錐滾子軸承為對象,而有關雙列圓錐滾子軸承的研究較少。鑒于此,本文針對某一型號汽車輪轂用雙列圓錐滾子軸承,基于滾動軸承動力學分析理論[9],考慮了6個自由度下的滾子、保持架的打滑、滾子的偏斜以及軸承內部摩擦與潤滑等因素,對雙列圓錐滾子軸承進行動力學分析,建立軸承非線性動力學微分方程,并在此基礎上建立雙列圓錐滾子軸承摩擦功耗數學模型。采用精細積分法和預估-校正Adams-Bashforth-Moulton多步法相結合的方法,對輪轂用雙列圓錐滾子軸承非線性動力學微分方程進行求解,并分析軸承不同工況參數、結構參數以及工藝參數對輪轂用雙列圓錐滾子軸承摩擦功耗的影響。

1 軸承動力學模型

圖1為雙列圓錐滾子軸承的軸向平面。雙列圓錐滾子軸承的兩個內圈通過鎖扣連結在一起,內圈固定,外圈以轉速ωe帶動保持架與滾動體進行旋轉。為了便于分析,引入以下主要坐標系:原點在軸承中間橫截面上的空間慣性坐標系{O;X,Y,Z},外圈坐標系{Oe;Xe,Ye,Ze},以及滾子坐標系(Xrm, Yrm,Zrm),下標m表示軸承列數,m=1,2(表示軸承列1和列2,下同).軸承使用過程中會受到以下外部載荷作用:

1)軸向預載荷F0,用軸向初始預緊量Δ0表示。

2)軸向載荷Fa和徑向載荷Fr.

3)繞Z軸方向的傾覆力矩MZ.

上述外部載荷除軸向預載荷作用在兩個內圈上外,其余均作用在軸承外圈上,見圖1.

軸承內、外滾道延長線及滾動體軸線相交于軸承中心軸線上一點A0,如圖2所示。滾子大端面中心到軸承軸線的徑向距離為

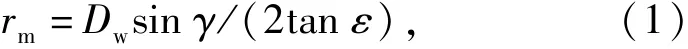
滾子大端面與內圈大擋邊的接觸高度h為

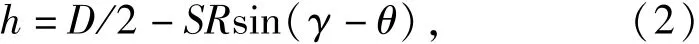
式中:D為滾子平均直徑,D=(Dw+Dw1)/2,Dw、Dw1分別為滾子的大端、小端直徑;SR為滾子大端球基面半徑;θ為內圈大擋邊傾角;ε為滾子半錐角;γ為軸承平均接觸角,γ=(α+β)/2,α、β分別為軸承的外接觸角和內接觸角。

1.1 軸承內部零件間相互作用

1.1.1 滾動體與滾道間的接觸載荷

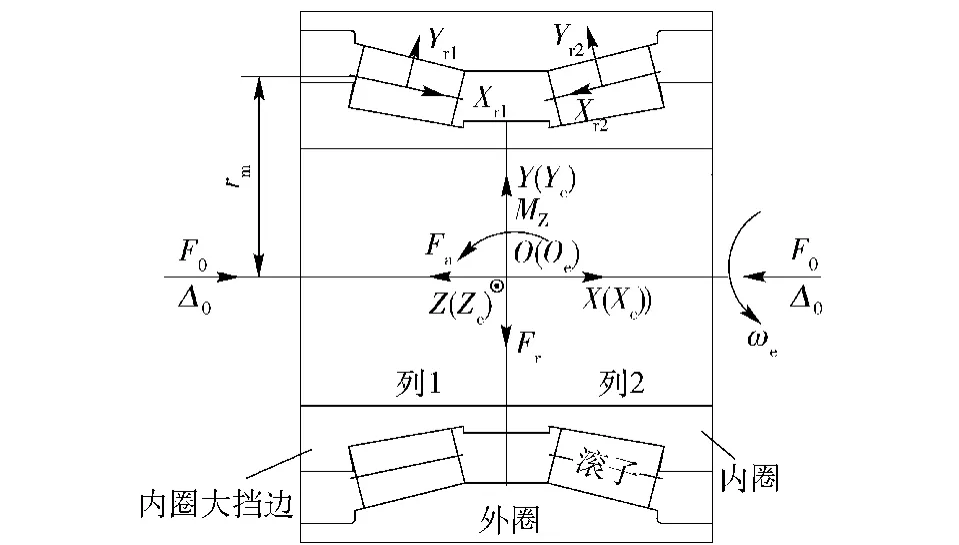
圖1 雙列圓錐滾子軸承坐標系和所受外載荷示意圖Fig.1 Coordinate system and external load of double row tapered roller bearing

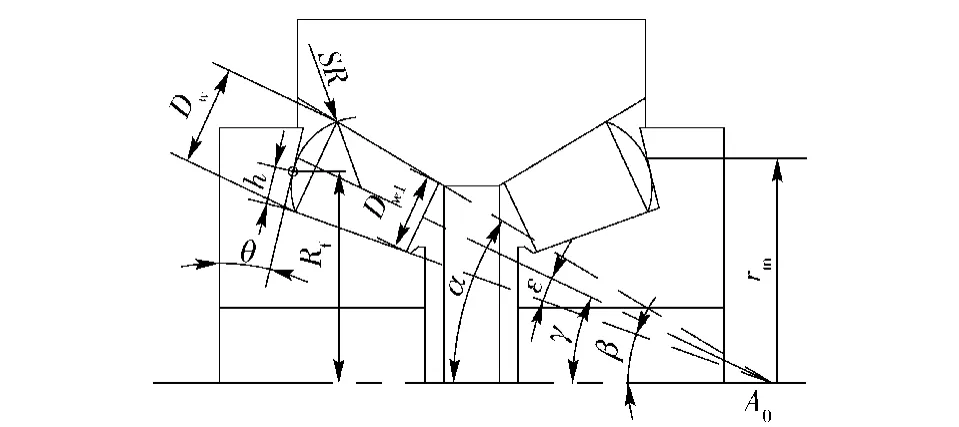
圖2 軸承幾何尺寸Fig.2 Geometrical dimensions of bearing

輪轂用雙列圓錐滾子軸承在使用過程中會受到軸向載荷、徑向載荷以及傾覆力矩的綜合作用,滾動體發生傾斜、歪斜,使軸承內部相互作用變得更為復雜。針對上述問題,本文采用“切片法”[10]計算滾子與滾道間的接觸載荷,如圖3所示。根據經典Hertz彈性線接觸理論,每一切片上滾動體與滾道間的接觸壓力為

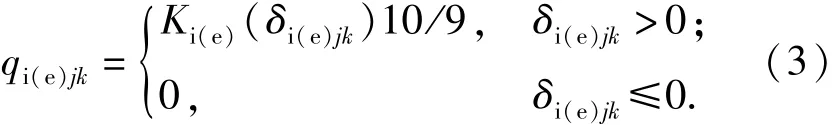
式中:qi(e)jk是第j個滾子第k個切片與內外滾道的法向接觸壓力;Ki(e)是滾子與內外滾道接觸處的負荷-變形常數,可由文獻[9]中的導出式得到;δi(e)jk是第j個滾子第k個切片與滾道間的彈性變形量,其計算方法見文獻[10];i,e分別表示內、外滾道(下同)。

滾子與滾道間的總接觸載荷可由滾動體有效接觸長度Ls上每一片與滾道的接觸壓力沿滾動體軸線方向進行積分求和得到,如(4)式所示:

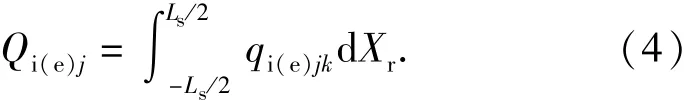
1.1.2 滾動體與滾道間的拖動力

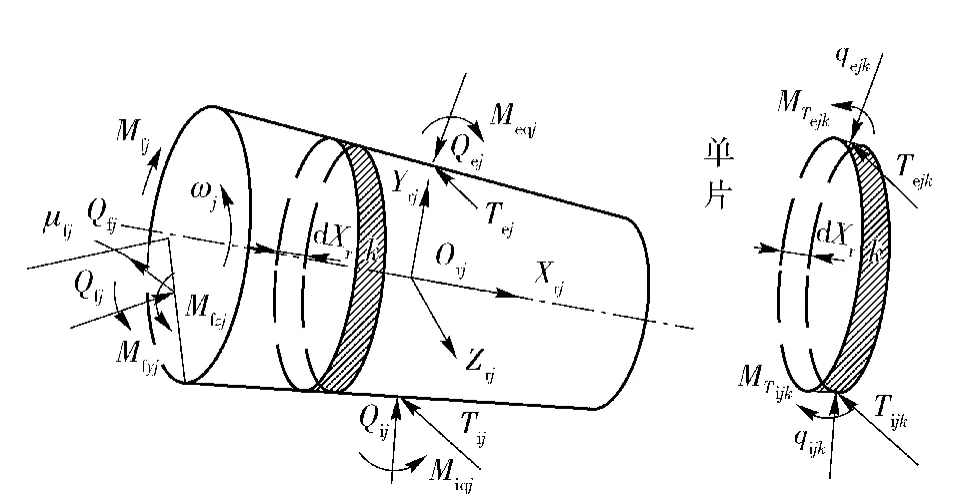
圖3 滾子與滾道間作用力Fig.3 Interaction between roller and raceway

滾動體與滾道間的潤滑劑被擠壓過程中會在接觸表面形成潤滑油膜。滾動體與內外滾道接觸處由于相對滑動引起的摩擦力可根據潤滑劑的拖動力來計算。如圖3所示,沿著滾動體軸線方向對滾動體進行切片,每一切片上的拖動力可表示為

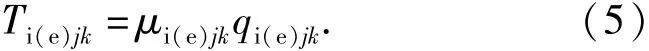
則滾子與滾道間的拖動力為每一片上拖動力的總和

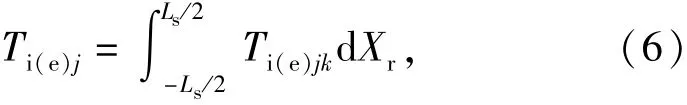
式中:μi(e)jk是第j個滾子第k個切片的潤滑油膜拖動系數[11]。

1.1.3 滾動體與內圈大擋邊間的接觸載荷

軸承在運轉過程中,滾動體通常與內圈大擋邊接觸。此處假設圓錐滾子大端面為球形基面,內圈大擋邊為錐形面。滾子與大擋邊間接觸處表面上會產生一接觸橢圓區,如圖4所示。在接觸橢圓區域內,假設滾動體與大擋邊間的作用力作用在最大彈性變形點處。則根據Klecker[12]的研究成果可得到滾子端部與大擋邊間接觸力為

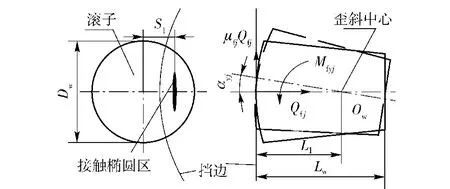
圖4 滾動體與大擋邊間作用力Fig.4 Interaction between roller and flange

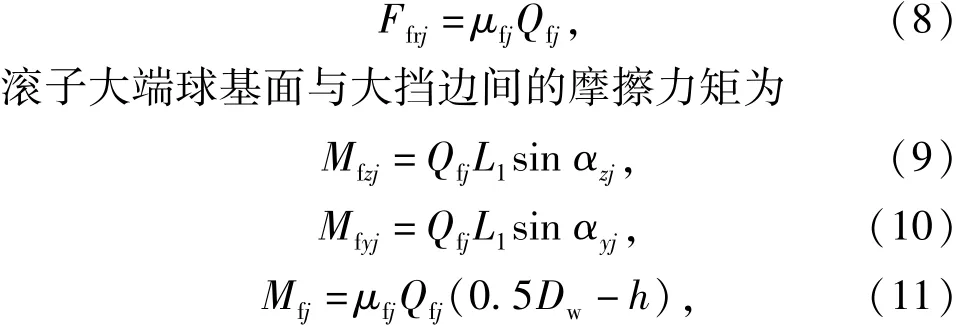
式中:μfj為滾子大端球基面與擋邊間接觸點的摩擦系數[13];L1為滾子偏斜中心距滾子大端的距離;αzj、αyj分別是滾子的傾斜角及歪斜角。L1和αzj,αyj可以通過仿真計算過程中測量得到。

1.1.4 滾動體與保持架間的接觸載荷

滾動體在滾道上滾動,同時又在保持架兜孔內繞自身軸線進行轉動。當滾子公轉速度大于保持架公轉速度時,滾子推動保持架向前運動;滾子公轉速度小于保持架公轉速度時,滾子阻礙保持架向前運動。滾動體與保持架兜孔之間既存在法向接觸載荷,也存在著切向摩擦力,如圖5所示。滾動體與保持架兜孔間的法向接觸載荷計算可采用滾動體與滾道間接觸載荷的“切片法”計算法,滾子與保持架兜孔間的接觸載荷計算為

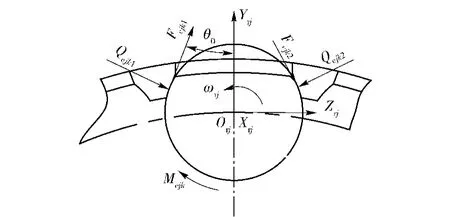
圖5 滾動體與保持架兜孔間作用力Fig.5 Interaction between roller and cage pocket

1.2 軸承動力學微分方程

根據軸承內部相互作用,得到圓錐滾子軸承第j個滾動體動力學微分方程00

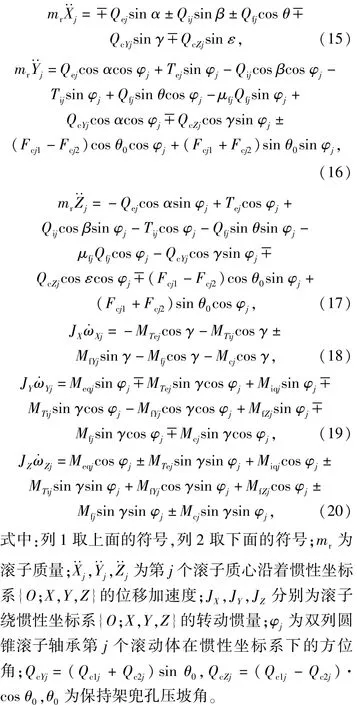
2 軸承摩擦功耗

軸承運轉過程中,滾動體與內外滾道、滾動體與內圈大擋邊以及滾動體與保持架兜孔接觸處的每一種摩擦力和阻礙力矩都會對軸承摩擦功耗產生影響,則軸承的總摩擦功耗為各接觸部位摩擦功耗的總和。

2.1 滾道處的摩擦功耗

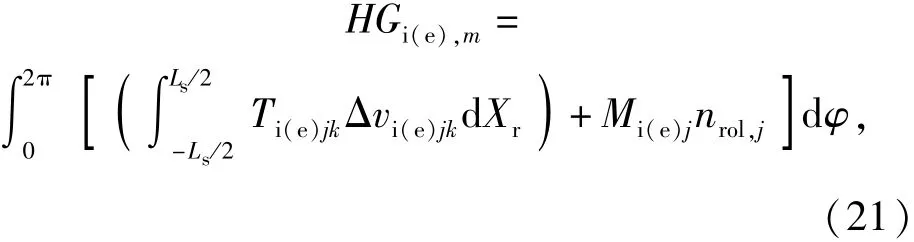
滾動體在內、外滾道接觸處,產生的摩擦功耗可由(21)式計算:式中:Γvi(e)jk是第j個滾子、第k個滾子切片在滾道接觸處的相對滑動速度,Γvi(e)jk=vi(e)k-vrjk;Mi(e)j是第j個滾動體在內外滾道接觸處的粘性滾動阻力矩[14]。

2.2 擋邊處摩擦功耗

內圈大擋邊與滾子大端球基面間由摩擦引起的功耗計算為

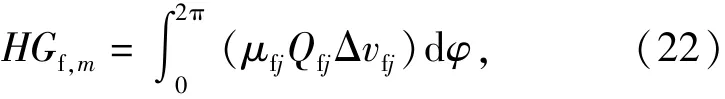
式中:Γvfj是第j個滾子大端面與大擋邊間的相對滑動速度,Γvfj=(ωi-ωc)Rf-S1ωrj,Rf為滾子大端端部與擋邊間接觸點到軸承軸線的距離,Rf=rm-S1cos γ,S1為滾子大端球基面與內圈大擋邊間的接觸點到圓錐滾子自身軸線的距離,S1=0.5Dwh·cos(γ-θ).

2.3 保持架兜孔處摩擦功耗

滾動體與保持架兜孔間的摩擦功耗計算為

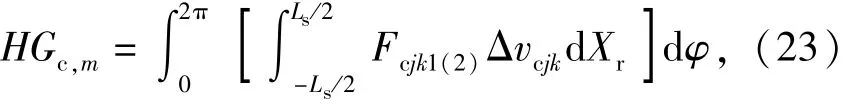
式中:Fcjk1(2)是第j滾子、第k個切片與兜孔間的切向摩擦力;Γvejk是第j滾子、第k個切片與保持架兜孔間的相對滑動速度。

2.4 軸承總摩擦功耗

將以上軸承各處的摩擦功耗進行疊加,即得到雙列圓錐滾子軸承的總摩擦功耗為

3 軸承摩擦功耗特性分析

本文根據所建立的軸承動力學模型和軸承摩擦功耗模型,采用了精細積分法和預估-校正Adams-Bashforth-Moulton多步法相結合的方法對軸承非線性動力學微分方程進行求解,計算軸承摩擦功耗。在此基礎上,開發了輪轂用雙列圓錐滾子軸承動力學分析軟件。

以某一型號輪轂用雙列圓錐滾子軸承為例,軸承保持架為沖壓筐形保持架,材料為增強尼龍;內、外圈及滾動體材料選用GCr15;內圈固定,外圈旋轉;保持架引導方式為滾子自引導。軸承幾何主參數見表1.

采用所開發的輪轂用雙列圓錐滾子軸承動力學分析軟件,對軸承工況參數(軸向預緊量、側向載荷比和傾覆力矩)、結構參數(滾子球基面半徑和大擋邊傾角)以及工藝參數(滾動體波紋度)與軸承摩擦功耗的關系進行了分析。

表1 軸承主參數Tab.1 Main parameters of bearing

3.1 軸承工況參數對軸承摩擦功耗的影響

雙列圓錐滾子軸承一般通過軸向預緊量來進行軸承預緊,提高軸承的承載能力。在不同工況參數下對輪轂軸承進行仿真分析,可得到軸承摩擦功耗隨工況參數的變化規律。

3.1.1 傾覆力矩對軸承摩擦功耗的影響

圖6～圖8是輪轂軸承在軸向載荷Fa=2 000 N,徑向載荷Fr=5 000 N,轉速n=1 000 r/min,不同軸向預緊量Δ0下,傾覆力矩對軸承摩擦功耗的影響。

從圖6～圖8中可以得到,隨軸承所受傾覆力矩的增加,軸承摩擦功耗逐漸增加。傾覆力矩小于300 N·m時,軸承摩擦功耗隨力矩的增加而緩慢增加。當傾覆力矩大于300 N·m時,隨傾覆力矩的增加,軸承摩擦功耗幾乎成線性增加。這是由于軸承所受傾覆力矩較小時,各個滾動體受力較小,隨著傾覆力矩的增大,滾動體受力增大,出現兩個承載區;軸向預緊量的增加使滾動體與滾道間接觸力增大,致使軸承內部接觸處的摩擦增加,軸承摩擦功耗就隨之增加。

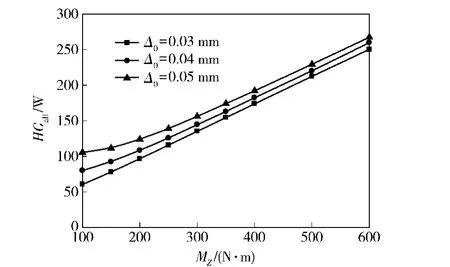
圖6 傾覆力矩對軸承總摩擦功耗的影響Fig.6 Effect of capsized moment on the whole friction power consumption of bearing

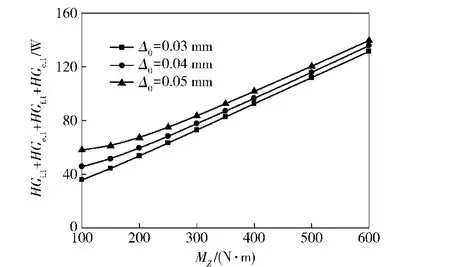
圖7 傾覆力矩對列1軸承摩擦功耗的影響Fig.7 Effect of capsized moment on friction power consumption of Row 1 bearing

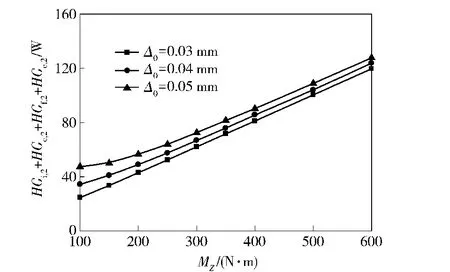
圖8 傾覆力矩對列2軸承摩擦功耗的影響Fig.8 Effect of capsized moment on friction power consumption of Row 2 bearing

3.1.2 側向載荷比對軸承摩擦功耗的影響

輪轂用雙列圓錐滾子軸承既能承受軸向載荷,又能承受徑向載荷。本文中,側向載荷比C定義為軸承所受的軸向載荷與徑向載荷的比值。仿真分析中,軸承承受傾覆力矩MZ=0 N·m,徑向載荷Fr= 5 000 N,轉速n=1 000 r/min,軸向預緊量Δ0= 0.03 mm.圖9是不同側向載荷比C下,軸承摩擦功耗的變化曲線。隨側向載荷比的增加,列1軸承的摩擦功耗逐漸增加,列2軸承摩擦功耗漸漸減少,而軸承總摩擦功耗略有增加。這是由于隨側向載荷比的增加,列1軸承被“壓緊”,滾動體與大擋邊處接觸載荷逐漸增加,摩擦增加,使滾子與大擋邊接觸處的摩擦功耗增加(如圖10所示),故列1軸承摩擦功耗增加;列2軸承被“放松”,滾動體所受接觸載荷減小,接觸處的摩擦減小,滾子與大擋邊處摩擦功耗降低(如圖11所示),故列2軸承摩擦功耗降低。其他接觸處摩擦功耗變化不大(見圖10和圖11),并且可以從數值上看出,列1功耗增加量比列2功耗減少量大,因此軸承總摩擦功耗略微增加。

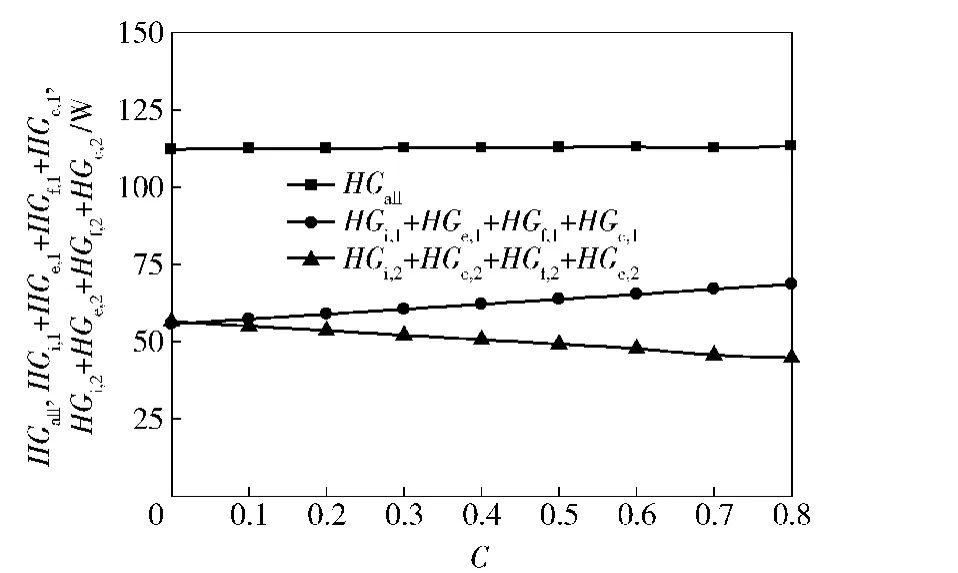
圖9 側向載荷比對軸承摩擦功耗的影響Fig.9 Effect of lateral load ratio on friction power consumption of bearing

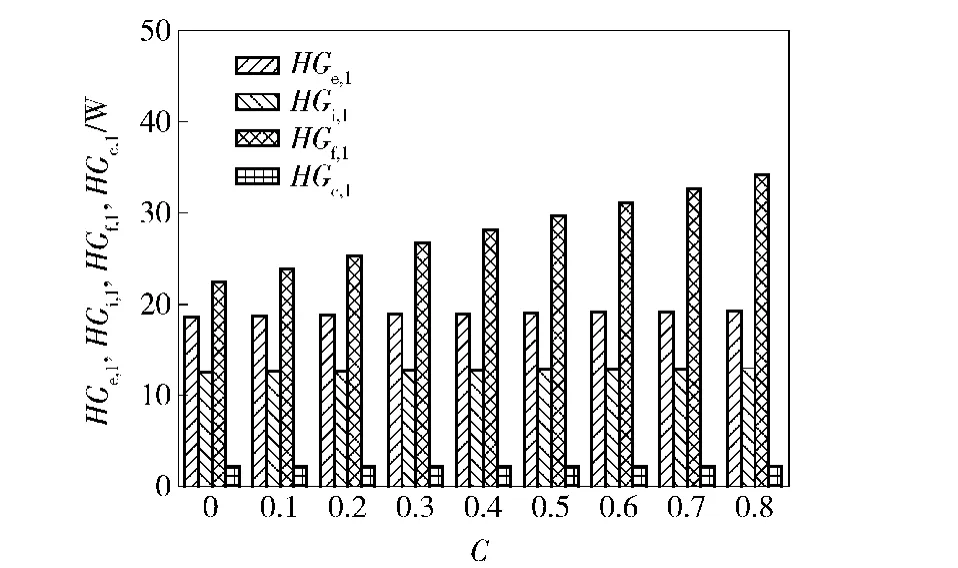
圖10 側向載荷比對列1軸承各處摩擦功耗的影響Fig.10 Effect of lateral load ratio on friction power consumption of Row 1 bearing

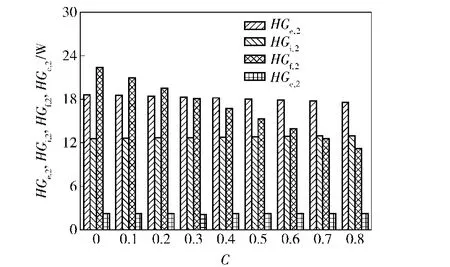
圖11 側向側向載荷比對列2軸承各處摩擦功耗的影響Fig.11 Effect of lateral load ratio on friction power consumption of Row 2 bearing

3.1.3 轉速對軸承摩擦功耗的影響

圖12～圖14是不同軸向預緊量Δ0下,轉速n對軸承摩擦功耗的影響規律。其中徑向載荷Fr= 5 000 N,軸向載荷Fa=2 000 N.從圖12中可以看出,隨轉速的增加,軸承摩擦功耗開始緩慢增加,隨后幾乎呈線性增加,同時軸向預緊量對軸承摩擦功耗的影響也越來越顯著。這是由于轉速的增加,使滾動體在滾道及擋邊上的滑動增加,加劇了滾動體與滾道及擋邊間的滑動摩擦;滾動體相對兜孔的滑動速度增加,滾動體與兜孔間的摩擦功耗增加。因此轉速的升高,軸承摩擦功耗也在不斷地升高。滿足使用要求下,圓錐滾子軸承應選擇低轉速,這也是大多圓錐滾子軸承適用于低速重載的原因。

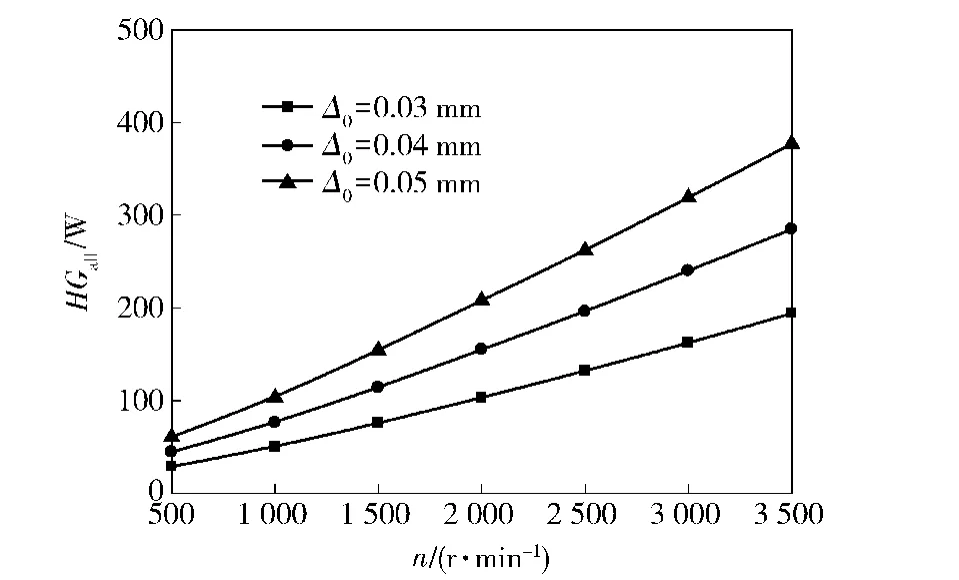
圖12 軸承轉速對軸承總摩擦功耗的影響Fig.12 Effect of rotating speed on the whole friction power consumption of bearing

3.2 結構參數對軸承摩擦功耗的影響

輪轂軸承在承受徑向載荷Fr=5 000 N、軸向載荷Fa=2 000 N、轉速n=1 000 r/min下,通過改變輪轂軸承的結構參數(大擋邊傾角及滾子球基面半徑),分析軸承結構參數對軸承摩擦功耗的影響。

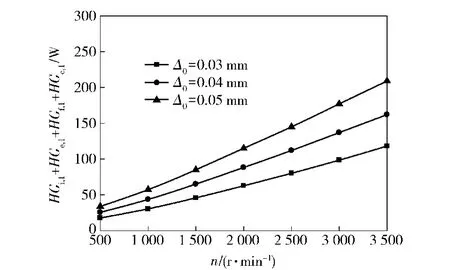
圖13 軸承轉速對列1軸承摩擦功耗的影響Fig.13 Effect of rotating speed on friction power consumption of Row 1 bearing

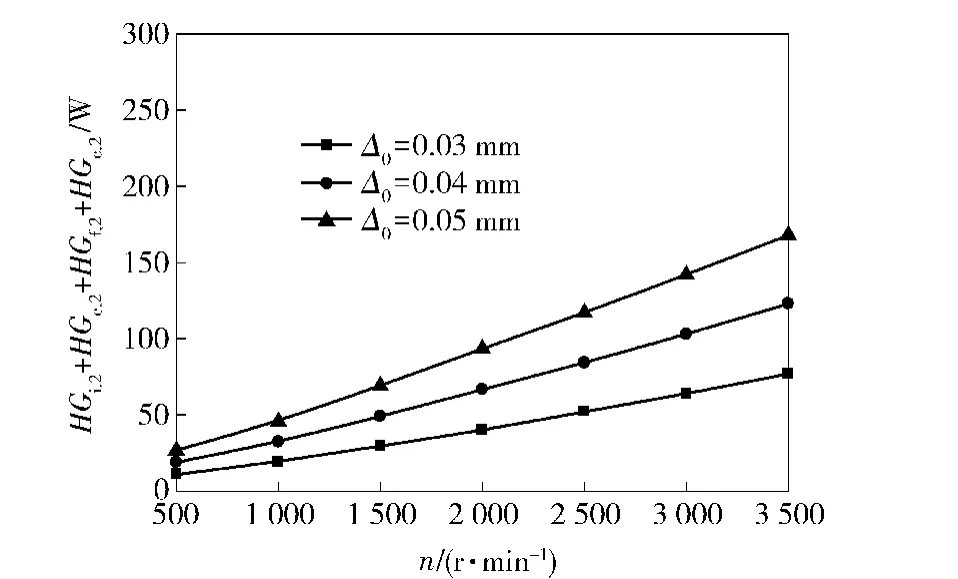
圖14 軸承轉速對列2軸承摩擦功耗的影響Fig.14 Effect of rotating speed on friction power consumption of Row 2 bearing

3.2.1 大擋邊傾角對軸承摩擦功耗的影響

由圖15～圖17可以得到,同一球基面半徑SR下,隨大擋邊傾角θ的增加,軸承摩擦功耗增加。這是由于球基面半徑不變時,隨擋邊傾角的增加,滾子與大擋邊間的相對滑動速度也增加(見圖18和圖19),致使接觸處摩擦增加,軸承摩擦功耗增加,但考慮到結構尺寸的限制,擋邊傾角不能無限增加。

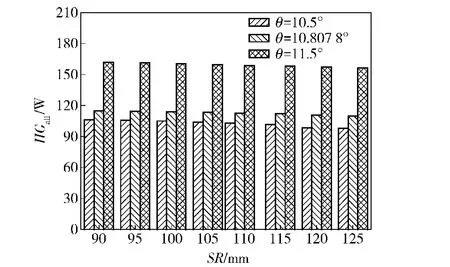
圖15 結構參數對軸承總摩擦功耗的影響Fig.15 Effect of structural parameters on the whole friction power consumption of bearing

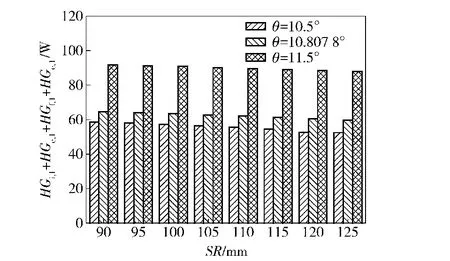
圖16 結構參數對列1軸承摩擦功耗的影響Fig.16 Effect of structural parameters on friction power consumption of Row 1 bearing

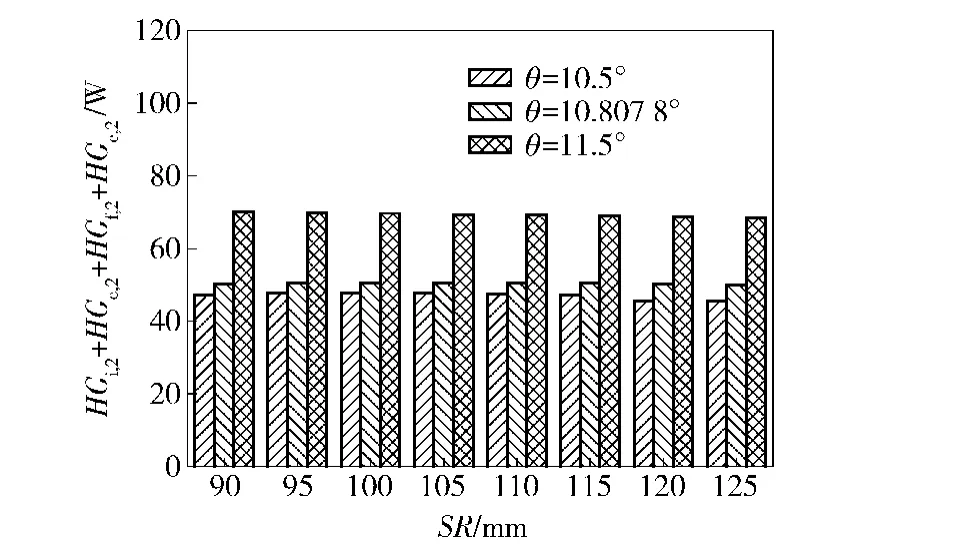
圖17 結構參數對列2軸承摩擦功耗的影響Fig.17 Effect of structural parameters on friction power consumption of Row 2 bearing

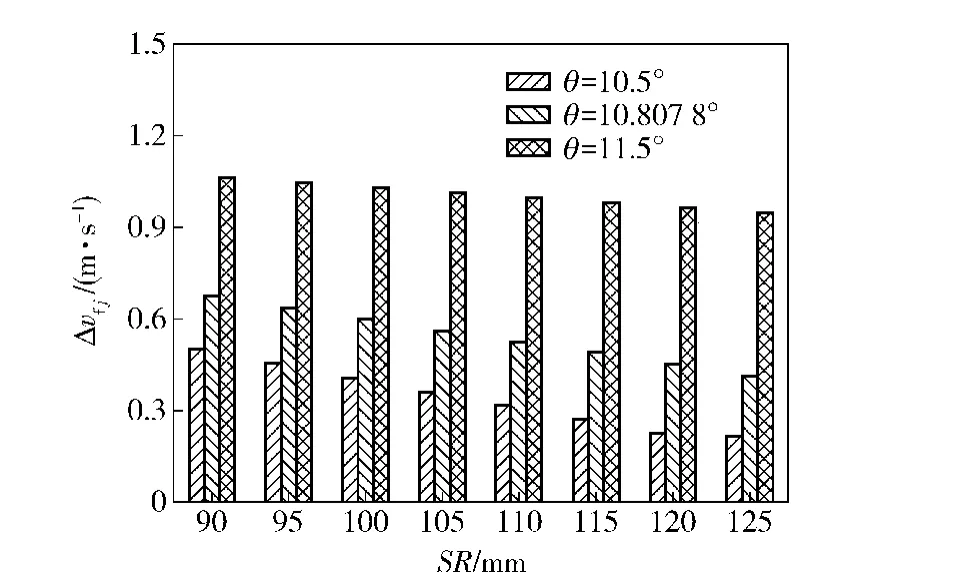
圖18 列1軸承滾子與大擋邊接觸處的滑動速度Fig.18 Sliding velocity between roller and end-flange of Row 1 bearing

3.2.2 滾子球基面半徑對軸承摩擦功耗的影響

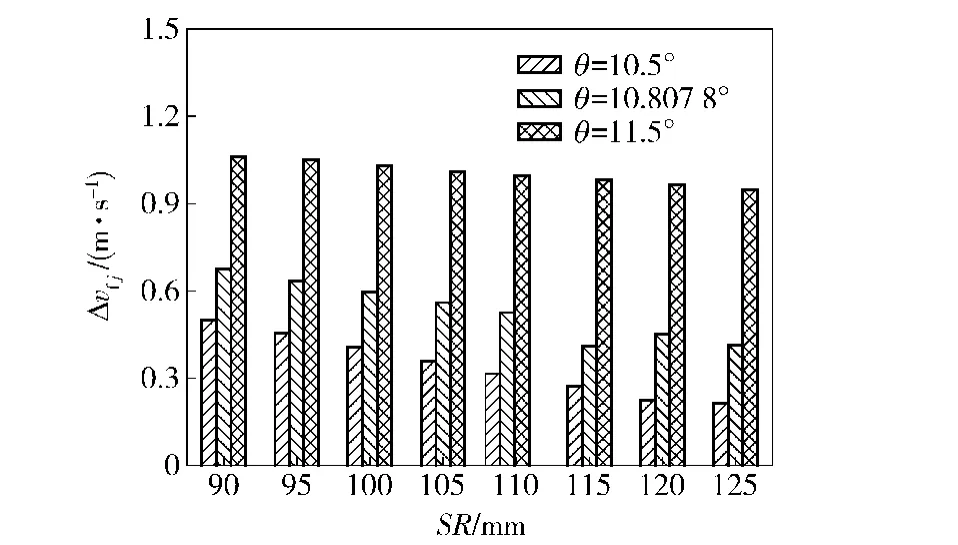
圖19 列2軸承滾子與大擋邊接觸處的滑動速度Fig.19 Sliding velocity between roller and end-flange of Row 2 bearing

由圖15～圖17可以看出,大擋邊傾角θ保持不變時,軸承摩擦功耗隨滾子球基面半徑SR的增加反而降低。這是由于球基面半徑的增加使滾子與大擋邊間的相對滑動速度Δvfj減小(見圖18和圖19),降低了滾子與大擋邊間的拖動作用,所以軸承摩擦功耗減少,但考慮到大擋邊與滾子端面間要有良好的潤滑狀態,球基面半徑不能無限增加。

3.3 工藝參數對軸承摩擦功耗的影響

軸承在加工時存在工藝誤差,使滾動體表面及內、外滾道表面形成波紋度,這些波紋度的存在對軸承內部相互作用有著復雜的影響。本文假設內、外滾道表面都是理想幾何形狀,僅考慮滾動體表面存在加工波紋度。軸承外圈轉速n=1 000 r/min,內圈靜止,初始軸向預緊量為0.03 mm,徑向載荷Fr= 5 000 N,軸向載荷Fa=2 000 N.對軸承進行仿真分析,研究滾子波紋度對軸承總摩擦功耗的影響。

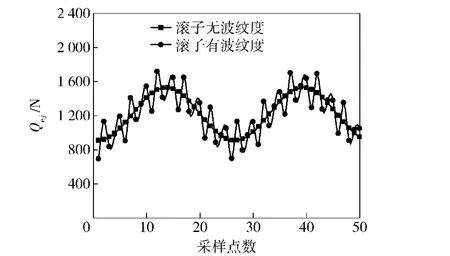
圖20 滾子波紋度對滾動體與滾道間接觸載荷的影響Fig.20 Effect of roller waveness on the contact load between roller and raceway

圖20和圖21為滾動體波紋度對軸承受載及總摩擦功耗的影響。從圖中可以看出,滾動體存在波紋度時,滾動體受載曲線和軸承總摩擦功耗曲線上下波動。表2是不同階次與幅值下滾動體波紋度對軸承總摩擦功耗的影響。從表中可得到:奇數階波紋度下,軸承總摩擦功耗隨波紋度的幅值的增加呈先升高后降低趨勢;偶數階次波紋度下,軸承總摩擦功耗隨波紋度幅值的增加而增加。

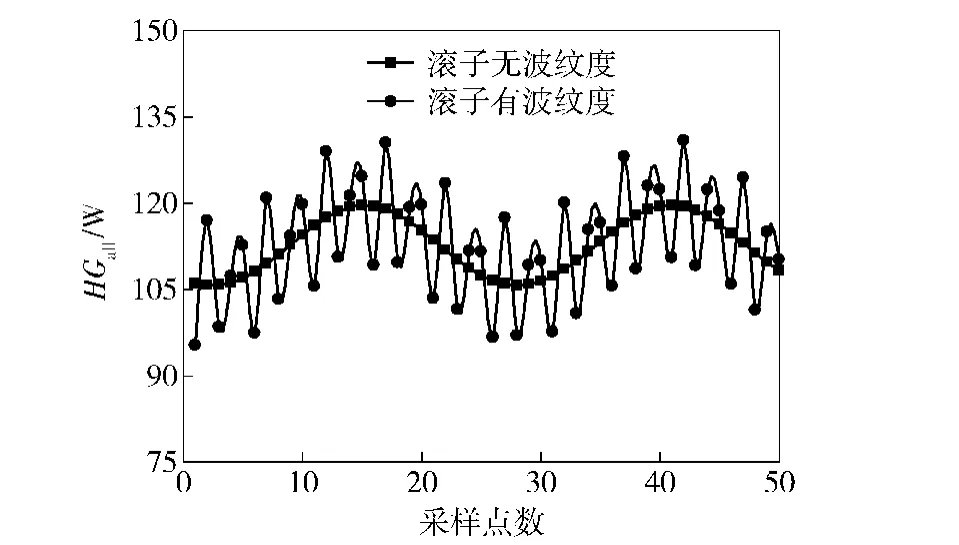
圖21 滾子波紋度對軸承總摩擦功耗的影響Fig.21 Effect of the roller waveness on the bearing friction power consumption

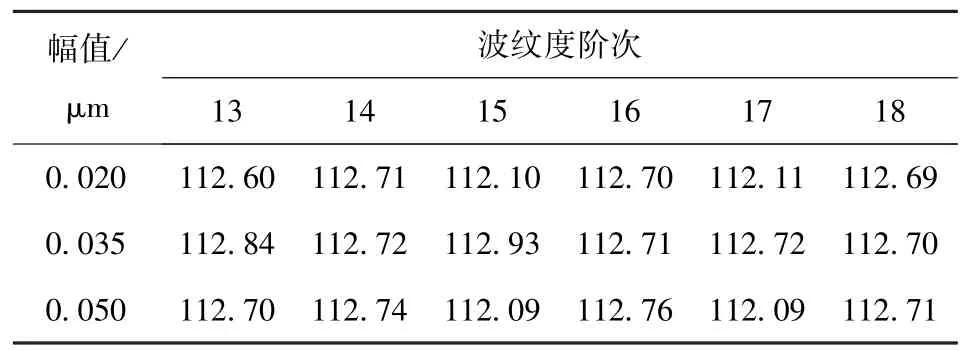
表2 滾動體波紋度對軸承總摩擦功耗的影響Tab.2 Effect of roller waveness on friction power consumption of bearingW

3.4 對比驗證

采用CRETU S所開發的雙列圓錐滾子軸承模型DRTRB與本文分析模型進行對比驗證。模型中軸承的主參數:滾子大端直徑8.106 mm,滾子全長10.929 mm,滾子球基面半徑115 mm,外滾道傾角14.051°,內滾道傾角10.051°,擋邊傾角10.10°,滾動體個數為16.軸承轉速為6 000 r/min,軸向載荷2 000 N,徑向載荷9 500 N,軸向預緊量0.03 mm.本文分析結果和CRETU S的計算結果如表3所示。從表3中可得到,本軟件與DRTRB模型所計算的結果基本相似,軸承總摩擦功耗誤差率不到5%,說明本文所建立的模型能較準確地描述輪轂用雙列圓錐滾子軸承的摩擦功耗。產生誤差的主要原因是本模型中保持架采用剛性體,保持架的柔性變形對仿真結果有一定的影響。

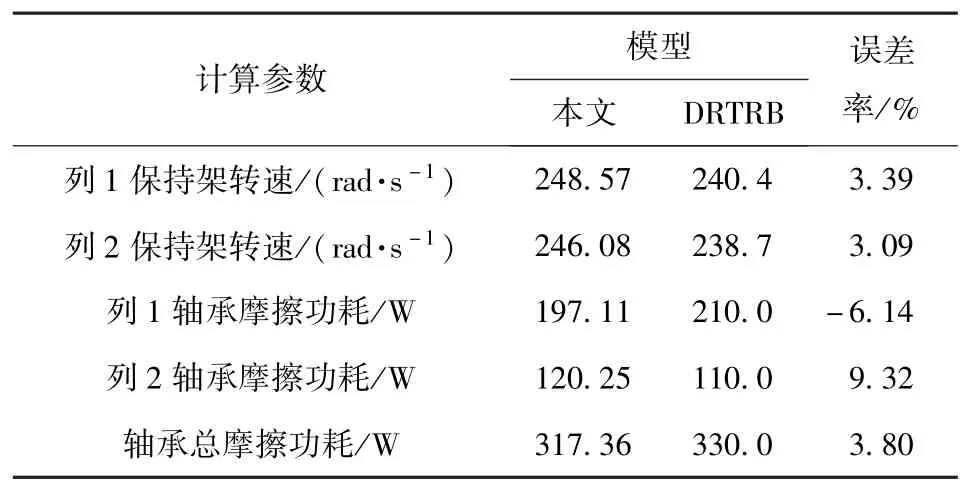
表3 計算結果對比Tab.3 Comparison of computed results

4 結論

本文在滾動軸承動力學理論基礎上,建立了雙列圓錐滾子軸承動力學仿真模型,并以某一型號輪轂用雙列圓錐滾子軸承為研究對象,分析了不同工況參數、結構參數及工藝參數對軸承摩擦功耗的影響,得出以下結論:

1)軸承摩擦功耗隨傾覆力矩、軸承轉速的增加先緩慢增加然后近似線性增加,并且軸承轉速對軸承摩擦功耗的影響較大。因此,在滿足使用要求下盡量選擇低轉速,這也是多數圓錐滾子軸承僅用于低速重載的原因。

2)側向載荷比的增加,使“壓緊側”軸承摩擦功耗增加,“放松側”軸承摩擦功耗降低,兩列摩擦功耗的差值變大,而軸承總摩擦功耗隨載荷比的增加略有增加。

3)軸承結構參數影響軸承摩擦功耗。軸承摩擦功耗隨球基面半徑的增加而減小,隨大擋邊傾角的增加而增加,但是考慮到軸承結構尺寸的限制和潤滑狀態的影響,球基面半徑和擋邊傾角不能無限制地增加,需對其進一步優化分析,獲得最佳大擋邊傾角和球基面半徑。

4)軸承加工工藝誤差影響軸承摩擦功耗。滾子波紋度在奇數階次時,軸承摩擦功耗隨波紋度幅值的增加呈先升高后降低趨勢。偶數階次波紋度時,軸承摩擦功耗隨波紋度幅值的增加而增加。

References)

[1] Gupta P K.Dynamics of rolling element bearings,partsⅠ,Ⅱ,Ⅲ,andⅣ[J].Journal of Lubrication Technology,1979,101(3):293-326. [2] Gupta P K.On the dynamics of a tapered roller bearing[J].Journal of Tribology,1989,111(2):278-287.

[3] Cretu S,Mitu N,Bercea I.A dynamics analysis of tapered roller bearing under fully flooded conditions[J].Wear,1995,188(1/ 2):1-18.

[4] Becea I,Cretu S,Nelias D.Analysis of double-row tapered roller bearings[J].Tribology Transactions,2003,46(2):228-247.

[5] Choi D H,Yoon K C A.Design method of an automo-tive wheel-bear-ing unit with discrete design variables using genetic algorithms[J]. Journal of Tribology,2001,123(1):181-187.

[6] 黎桂華,黃平,趙聯春,等.轎車輪轂軸承外部載荷計算方法及其特性[J].潤滑與密封,2006,29(11):17-20.

LI Gui-hua,HUANG Ping,ZHAO Lian-chun,et al.Calculation method and characteristic of the car's wheel-bearings external load[J]. Lubrication Engineering,2006.29(11):17-20.(in Chinese)

[7] 陳雪峰.汽車輪轂軸承疲勞失效分析及預防研究[D].蘇州:蘇州大學,2010.

CHEN Xue-feng.Failure analysis and prevention of wheel bearing of automobile due to fatigue[D].Suzhou:Suzhou University,2010. (in Chinese)

[8] 武福,楊喜娟,毛旭強.高速列車轉向架軸箱軸承的熱分析建模與仿真[J].機械研究與應用,2011,27(5):38-41.

WU Fu,YANG Xi-juan,MAO Xu-qiang.Thermal modeling and analysis of bearing used at CRH train bogie[J].Mechanical Research and Application,2011,27(5):38-41.(in Chinese)

[9] 鄧四二,賈群義.滾動軸承設計原理[M].北京:中國標準出版社,2008.

DENG Si-er,JIA Qun-yi.Design and theory of rolling bearings[M]. Beijing:Standard Press of China,2008.(in Chinese)

[10] 鄧四二,付金輝,王燕霜,等.航空發動機滾動軸承-雙轉子系統動態特性分析[J].航空動力學報,2013,28(1):195-204.

DENG Si-er,FU Jin-hui,WANG Yan-shuang.Analysis on dynamic characteristics of aeroengine rolling bearing/dual-rotor system[J]. Journal of Aerospace Power,2013,28(1):195-204.(in Chinese)

[11] DENG Si-er,TENG Hong-fei,WANG Yan-shuang,et al.Constitutive equation of a new aviation lubricating oil[J].Chinese Journal of Mechanical Engineering:English Edition,2007,20 (5):28-31.

[12] Klecher R J.High speed cylindrical roller bearing analysis,SKF computer program“CYBEAN”,NASA-CR-159460[R].Washington DC:NASA,1978.

[13] 胡浪,王文中,趙自強,等.雙列圓錐滾子軸承滾子大端-引導邊潤滑接觸分析[J].摩擦學學報,2013,33(1):22-28.

HU Lang,WANG Wen-zhong,ZHAO Zi-qiang,et al.Lubricated contact analysis of roller large end-flange in double-row tapered roller bearing[J].Tribology,2013,33(1):22-28.(in Chinese) [14] Matsuyama H.High efficiency and tribology in rolling bearings[J]. JTEKT Engineering Journal:English Edition,2012,1009E: 108-113.

Research on Power Consumption Characteristics of Double-row Tapered Roller Bearings

DENG Si-er1,2,HU Guang-cun1,DONG Xiao1
(1.School of Mechatronics Engineering,Henan University of Science and Technology,Luoyang 471003,Henan,China; 2.Zhejiang Zhaofeng Mechanical and Electronic Co.,Ltd.,Hangzhou 311232,Zhejiang,China)

Based on the dynamic theory of rolling bearings,the nonlinear dynamic equations and friction power consumption mathematical models are established for double-row tapered roller bearings.Fine integral method and predict-correct Adams-Bashforth-Moulton multi-step method are used to solve the equations.The influences of different working conditons,structural parameters and process parameters on bearing friction power consumption are analyzed.The results show that the friction power consumption increases slowly and then linearly increases with the rise in capsized moment and rotating speed.The rotating speed has an obvious effect on friction power consumption,and a lower speed should be selected as much as possible under the premise of meeting the operating requirements.The increase in lateral load ratio makes the friction power consumption of impacted side increase and the friction power consumption of unfixed side decrease.The difference of friction power consumptions of the two sides increases.The bearing friction power consumption increases with the rise in big rim angle,and decreases with the in-crease in curvature radius of roller end surface.For the odd waviness orders of rollers,the friction power consumption of bearing firstly increases and then decreases with the increase in the waviness amplitude; for the even orders,the friction power consumption of bearing increases with the rise of the waviness amplitude.

mechanics;bearing dynamics;double-row tapered roller bearing;power consumption

TH133.33

A

1000-1093(2014)11-1898-10

10.3969/j.issn.1000-1093.2014.11.023

2014-01-13

國家“十二五”科技攻關項目(JPPT-ZCGX1-1);河南省科技創新人才計劃項目(144200510020)

鄧四二(1963—),男,教授,博士生導師。E-mail:dse@mail.haust.edu.cn;

胡廣存(1989—),男,碩士研究生。E-mail:huguangcun@126.com