瞬變電磁視時間常數tau成像分析與應用研究

劉 沖， 王宇航， 皇 健，羅 勇

(1.成都理工大學 地球物理學院， 成都 610059；2.四川省地震局，成都 610041)

0 引言

目前瞬變電磁成像與反演發展較慢，基本局限于一維成像和反演，而反演速度較慢，嚴重制約了電磁數據的分析處理，因此力求探索一種快速的、高效的電磁數據處理方法，甚至通過處理現場測量數據來迅速了解測區地質異常體的大體分布規律，或為后續反演提供約束參數。需要探索地質體巖性參數與電磁響應之間的關系，充分利用這一物理規律來達到尋找異常體。靜恩杰、李志聃[1-2]通過分析礦體內的感應電流，應用電路理論解釋瞬變電磁場的物理過程，得出了礦體時間常數tau與導電性的關系，指出導電性差的礦體，其時間常數值較小；導電性良好的礦體，其時間常數值較大，并給出了一般良導體時間常數的表達式τ=KAσμ和幾種規則異常體的時間常數表達式；靜恩杰等和牛之璉[2-3]分析了電磁響應與時間常數的關系，并導出了在瞬變場衰減晚期的關系式A(t)=A0e-(t/τ)。Jiuping Chen等[4]探討了瞬變電磁時間常數的估算，并應用矩陣束在tau域中對大地電磁數據進行了特征參數提取與重構；J.Sott Holladay等[5]對局部異常體的時間常數進行了預測估計，通過時間常數tau來分析異常體；牛之璉[3]提出了任意局部導體的晚期瞬變電磁響應與時間常數的關系表達式V(t)∝e-(t/τ)/τ，指出時間常數tau與異常體巖性參數和物性參數有關。以上所有的分析研究僅局限于瞬變電磁一維展開，并將晚期按統一的時間常數tau來衰減。作者基于以上理論，通過分析時間常數與電磁響應的規律，得出視時間常數tau值成像，在剖面和時間(水平)切片上對時間常數進行了分析，為圈定地質異常體提供了有效的方法，并為瞬變電磁反演約束參數的限定提供了依據。

1 時間常數tau的理論基礎

1.1 tau的物理意義

一次磁場在周圍傳播過程中，如遇到地下良導電的地質體，將在其內部激發產生感應電流，又稱渦流或二次電流。二次電流隨時間變化，因而在其周圍又產生新的磁場，稱為二次磁場。由于良導電礦體內感應電流的熱耗損，二次場大致按指數規律隨時間衰減。二次場主要來源于良導電體的感應電流，因此它包含著與礦體有關的地質信息。根據二次場的衰減規律進行分析處理，可以解釋地下礦體及相關物理參數。

據法拉第電磁感應定律，當發射電流突然關斷時，地下良導體將產生感應電流，感應電流在地下礦體內擴散過程可分為三個階段[1]，為了維持礦體內原磁場，在斷電初期，感應電流集中分布于礦體表面形成表面電流，該階段稱為早期時間；隨著感應電流在礦體內的熱損耗，表面電流開始向礦體內部擴散，其擴散速度一般與礦體的導電濾波成反比關系，稱中期階段；當礦體內感應電流擴散經過一段時間后便進入所謂的晚期階段，其感應電流的每個線電流的阻抗和感抗均趨于漸近值，是晚期階段主要特征，此時礦體內電流分布趨于相對穩定，熱耗損速度減慢，表現為與感應電流相對應的二次場衰減速度減緩。

礦體內感應電流及與之對應的二次場隨時間變化率，取決于礦體的巖性和物性參數(如電導率、磁導率、礦體尺寸大小及形狀等)。早期礦體表面電流的分布僅與礦體的形狀和大小有關，而與礦體的電導率幾乎無關。

瞬變電磁曲線變化速率的大小，取決于異常體的電性好壞和幾何形狀，其電性和幾何形狀反應在它的時間常數上，因此，異常體的時間常數決定瞬變長衰減速率的大小，是確定異常體電性好壞的重要參數。幾何形狀相同的礦體，導電性越好，其時間常數越大，一般導體的時間常數可表示為[2]：

τ=KAσμ

(1)

式中K為隨異常體而變的常至數；A為與異常體幾何形狀有關的參數；σ為為電導率，μ為磁異常，也可用μ0近似代替(單位ms)。

1.2 tau與地質異常體的瞬變電磁響應關系分析

根據以上分析，對于球體導體中感應渦流進入晚期后，渦流分布狀況已處于穩定，并且按指數規律衰減。這種結論也適合于其他形狀的有限導電體。那么就有可能用(圖1)一個包含有等效電感L和等效電阻R的單匝電流環來等效這種晚期渦流。兩者的外場具有相似的規律[3,6]。

圖1 有限導體的等效電路[3]Fig．1 The equivalent circuit of the conductor(a)有限導體的等效回路示意圖；(b)板狀體和球體的Mn方向示意

設：φ1為等效回路切割一次場的磁通量；切斷時間為tof；在切斷時間內，等效回路中產生的感應電動勢為φ1/tof；感應偶極矩為Mn；激勵場的法向分量為H1n。

利用等效回路的瞬態方程[3]：

(2)

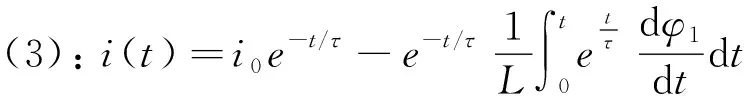
(3)

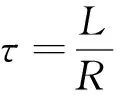
在供電時間內(t<0)，回路中沒有感應電流產生，在H1切斷的時間tof內，感應電流由一次場通量變化率確定。切斷一次場后(t>tof)，公式(2)可變為式(4)。

(4)

等效回路中感應電流為：

(5)

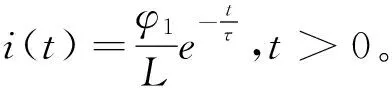
據電磁感應定律：

得到一次場脈沖間歇時間(t≥tof)感測到的感應電壓：

V(t)=-A0/tof(etof/τ-1)e-t/τ

(6)

在tof≤τ的情況下：

V(t)=A0/τe-t/τ

(7)

式中：I1發送電流；tof為關斷時間。

Holladay和Chen[4]提出對于一個獨立的目標體的瞬變電磁響應，其測量磁場B和感應電壓V可以分解為單個極性響應的加權總和。

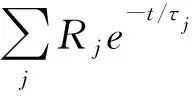
(8)

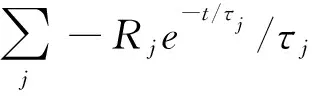
(9)

V(t) =AeffdB/dt

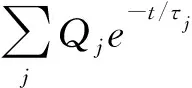
(10)

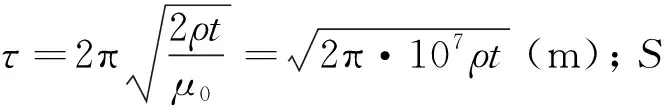
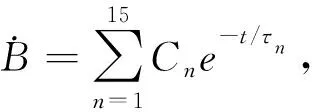
(11)

由式(7)、式(9)和式(11)可以看出，局部導電體上瞬變電磁響應的異常幅度及衰減速度，很大程度上決定于導體的時間常數τ。

對于不同導電性地質異常體而言，其時間常數tau值較小，盡管二次場初值較大，但其衰減速度較快(如圖2中測點b所示)；反之，導電性良好礦體，時間常數tau值較大，盡管二次場初值較小，但衰減速度慢(如圖2中測點a、c所示)。而一般導電性礦體典型的衰減時間范圍從100 μs～200 μs至10 ms～20 ms[3]。

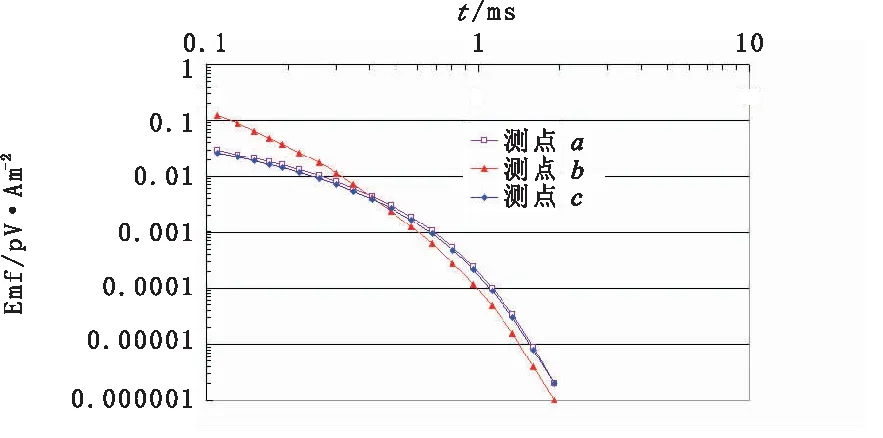
圖2 瞬變電磁場衰減規律與時間常數tau的關系圖Fig．2 Diagram for the relation between transient electromagnetic field attenuation andtime constant tau

對于式(7)、式(9)和式(11)所表示的是單一地質異常體的瞬變電磁響應與時間常數tau的關系，即時間常數tau是唯一的。在地下不同深度，相對于復雜的地質構造，其時間常數tau是變化的，所以式(7)、式(9)和式(11)中的tau值在不同時間點是不相同的，即對應不同深度反映的時間常數tau應不相同。而式(7)、式(9)和式(11)中，在瞬變電磁進入晚期時才有此規律，所以在瞬變電磁晚期分時窗進行時間常數求取，得到晚期不同時間點，即不同深度處的時間常數，以得出在晚期對應深度上的異常體分布規律。由于良導電性異常體的響應有延遲效應，晚期道時間常數不但有時間窗內異常地反映，同時還包含了部分早期良導電性礦體響應信息，因此時間常數是一個地下測區所有礦體的綜合響應。但瞬變電磁在晚期道信號弱，并且易受干擾，當信噪比較差時，出現了衰減負值時，該方法即失效。

針對于不同的地質異常體(二度體或三度體)可應用公式(7)、式(9)和式(11)得出各時間點的時間常數，然而電磁響應是體積效應，提取各時間窗(t1,t2)內的時間常數τ，對應的不是單個時間點的時間常數，而是對應該時窗內異常體衰減系數的綜合反映，因此可以稱為視時間常數。其反應的主要特征為這一時間窗內對應的所有地質異常體的響應。

2 時間常數tau的應用

2.1 薄板模型數值模擬試算

根據以上理論，建立模型如圖3所示，為一薄板模型，測區為 1 000 m×300 m，模型埋深為100 m，長寬E-N為200 m×200 m，薄板中心位置為EN(10 400，10 200)，電導為10 S，其背景層為空氣層，共4條測線平行排列，從左至右依次編號為測線1、測線2、測線3、測線4，測線長為 1 000 m，測線間距100 m，測線1與薄板異常體邊緣的水平間距為100 m，測線2、測線3位于異常體邊緣正上方，測線3橫穿異常體中心。該模型所采用的數值模擬方法為Maxwell軟件中內置的全空間薄板正演模塊。

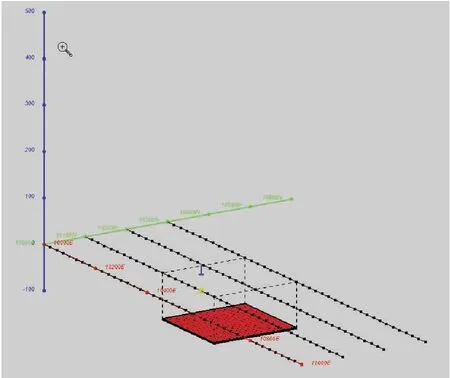
圖3 薄板正演模型Fig．3 Thin sheet model

通過正演模擬和tau值求取，得到如圖4所示的視時間常數tau值剖面圖，從圖4中可以看出，薄板的橫向(測線方向E)最大異常寬度在300m左右，與薄板的實際E向長度相差100 m。這是由于低阻異常體對電磁場有吸附作用，導致薄板附近較遠距離處的測點都受到低阻薄板的影響，由于電磁場體積效應，使得視時間常數是測點附近所有異常體的綜合響應，圖4中視時間常數是針對晚期時間道做的，所以薄板的垂向(深度方向)并沒有很好地反映出來。當測線向薄板異常體邊緣靠近時，視時間常數tau異常范圍逐漸變窄(如圖5所示)，邊緣處時間常數tau值異常寬度在200 m左右，與薄板異常體寬度吻合良好；當測線遠離異常體時，時間常數tau的畸變趨于微弱，接近平穩，即受薄板異常影響微弱。圖6為圖5在時間t=1.9 ms的水平切片圖，從圖6中可以直觀地看出時間常數tau在晚期道水平切片上的變化規律，即薄板中心處時間常數tau最大，遠離薄板，時間常數tau值逐漸減小，其時間常數tau異常區在平面的展布與薄板相似。從圖6表示的晚期時間常數tau的水平切片圖，能很好地反應晚期時間道(即深部)地質體在水平空間上的分布。

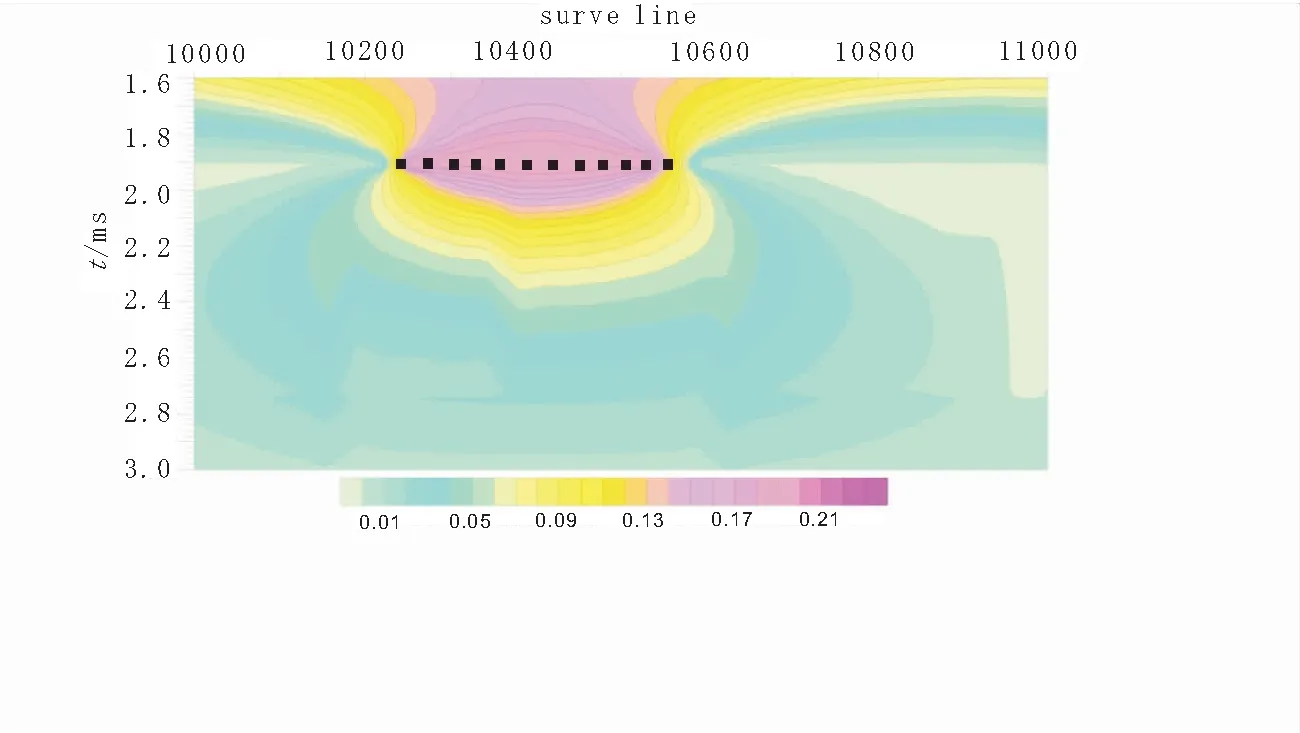
圖4 測線3對應晚期道視時間常數tau/ms剖面圖Fig．4 The corresponding the time constant (tau/ms) profile in the late of line 3

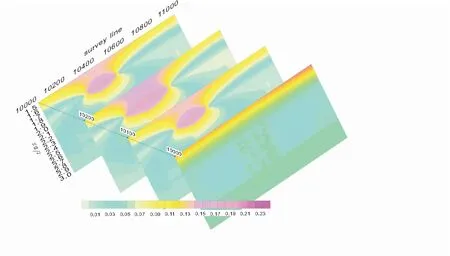
圖5 薄板狀異常體的視時間常數tau/ms的空間展布Fig．5 The spatial distribution of the apparent time constant tau/ms for the sheet abnormal body

2.2 時間常數 tau的實際應用分析

圖7為某地區的實測瞬變電磁原始數據時間剖面圖，僅從時間剖面圖中可以看出，在測點 2 500 附近和 4 000～4 500 處有異常的響應，其中測點 2 500 附近的響應強，從早期到晚期均有響應，而測點 4 000～4 500 處，早期響應異常較明顯，晚期時接近于無變化。

應用該地區瞬變電磁響應得出如圖8所示的視時間常數tau在不同時間道上沿測線方向的變化規律。在圖8(a)中，時間常數tau值在整個測線上都有較明顯異常，在測點 2 500 附近異常最明顯，與圖7中所反映的異常現象相吻合，隨著時間的推移，在圖8中，測線兩邊的異常相對逐漸減弱，而突出了測點 2 500 附近的異常，由此可以得出，測線兩邊異常主要體現在較早期道，即相對淺部信息或與圍巖差異較小的異常體；而測點 2 500 附近時間常數tau值的異常體現了較深部信息或與圍巖異常差異很明顯的低阻異常體，在響應上有較大的延遲。可以得出，較早期道的時間常數tau值受一次場的影響，其變化較晚期道的時間常數tau值不明顯，隨著時間增大，時間常數tau變化也越來越明顯，最后突出反映晚期道異常體。圖9為對應視時間常數tau剖面圖，更能直觀地反映出低阻異常體橫向的分布規律，可以推斷時間常數tau值異常處為一低阻異常體，與實際地質情況吻合良好。

3 結論與展望

瞬變電磁響應與時間常數密切相關，而時間常數反應著地下介質介電常數、電導率、異常體的幾何形狀及埋深等，因此對時間常數τ的分析有著很大的意義。作者在分析視時間常數tau的基礎上得出以下三點結論：

(1)針對瞬變電磁二次場與地質異常體的響應關系，結合異常體內在的巖性和物性參數，得出了視時間常數tau成像方法，并作出了時間剖面和時間道切片，通過數值模擬和實測數據的計算，得出了較好的效果。

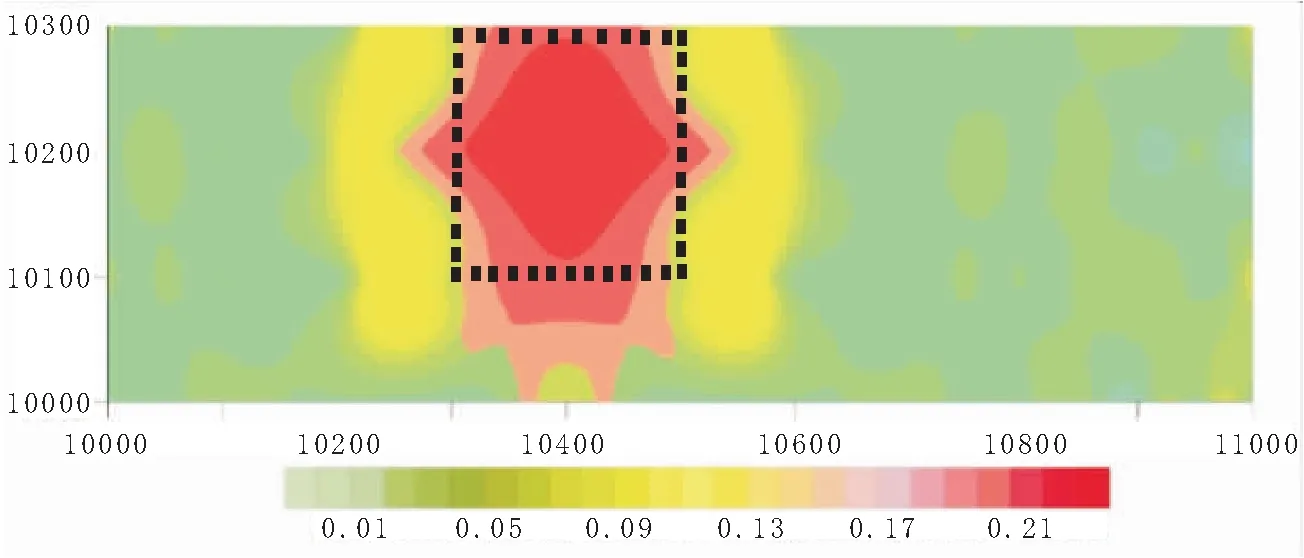
圖6 中心時間t=1.900 ms的tau/ms值水平切片成像Fig．6 Tau/ms horizontal slice imaging at the center timet=1.900 ms

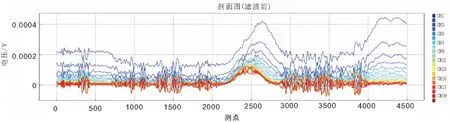
圖7 某地區實驗數據抽道時間剖面圖Fig．7 The extractive time-windows profiles for the experimental data at a certain area

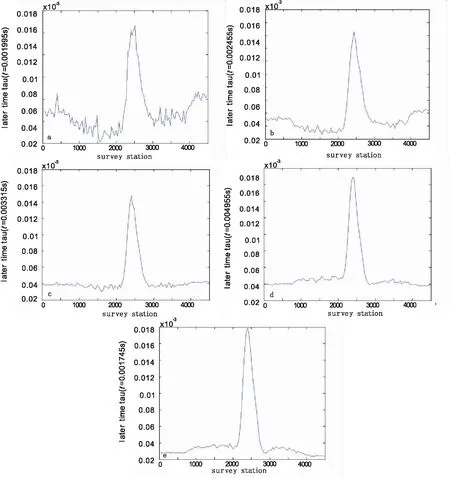
圖8 某地區測線的不同時間道上tau/ms的變化規律Fig．8 Tau/ms change principles at different time on the survey line of a certain area(a)t=1.745 ms；(b)t=1.995 ms;(c)t=2.455 ms;(d)t=3.315 ms;(e)t=4.915 ms

圖9 某地區視時間常數tau/us值剖面圖Fig．9 A region as the apparent time constant tau/us profile

(2)通過數值模擬，得出視時間常數tau能較好地反映晚期時間道(即深部)上地質異常體橫向上的分布規律，但不能很好地反應異常體的深度。

(3)對于薄板狀低阻異常體，其瞬變電磁二次場在時間上有延遲效應，即地下某一深度的地質體可能影響到很長時間內的τ。那么提取的時間常數τ就不單是反應該時間窗對應的地質體，還受薄板響應的延遲影響。

接下來的工作展望，根據地質體的瞬變電磁響應規律，充分利用二次場數據，以期得出早期的視時間常數tau與瞬變電磁場的對應關系，以求取早期的視時間常數變化特征，并探索視時間常數tau與地質異常體埋深的對應關系。

參考文獻：

[1] 靜恩杰,李志聃.瞬變電磁法基本理論[J].中國煤田地質,1995,7(2):83-87.

[2] 靜恩杰,李志聃.瞬變電磁法資料處理和解釋[J]. 中國煤田地質,1995,7(4):97-101.

[3] 牛之璉.時間域電磁法原理[M].長沙:中南大學出版社,2007.

[4] JIUPING CHEN, JAMES MACNAE. Automatic estimation of EM parameters in Tau Domain[J]. Exploration Geophysics，1998,29:170-174.

[5] SOTT J. HOLLADAY,WILLIAM E. DOLL,LES P. BEARD,et al.UXO Time-Constant Estimation from Helicopter-Borne TEM Data[J].Journal of Environmental and Engineering Geophysics，2006, 11(1):43-52.

[6] 鄭凱.回線源時間域航空電磁數據處理研究[D].成都:成都理工大學,2010.

[7] PELTON W H.Mineral discrimination and removal of inductive coupling with multifrequency IP[J]. Geophysics,1987:201-205.

[8] DANIEL LEMIRE,PH D. Baseline asymmetry, Tau projection, B-field estimation and automatic half-cycle rejections[M]. Signal processing and industrial R&D consultants,2011.

[9] ALLARD M. On the Origin of the HTEM Species. Advances in Airborne [J].Geophysics.2007:355-374.