3種計算滲透率變異系數方法的對比

桂東旭 (中石油大慶油田有限責任公司勘探開發研究院,黑龍江大慶 163712)

3種計算滲透率變異系數方法的對比

桂東旭 (中石油大慶油田有限責任公司勘探開發研究院,黑龍江大慶 163712)

滲透率變異系數是描述油藏宏觀非均質性的一個重要參數,目前有計算滲透率變異系數的方法有統計學理論公式法、Dykstra-Parsons定義法和lorenz系數法3種,通過詳細介紹并對比不同方法的計算步驟與原理,給出了每種方法的優缺點和適用范圍,并以東部層狀砂巖油田7個處于特高含水開發階段的區塊為例進行驗證和比較。結果表明,統計學理論公式法與Dykstra-Parsons定義法得到的結果與實際地質認識稍有不同,lorenz系數法與地質認識相一致。通過理論與實際對比分析推薦采用lorenz系數法來計算滲透率變異系數。

滲透率;變異系數;計算方法

儲層宏觀非均質性是儲層非均質性的重要組成部分,主要是指儲層巖性、物性、含油性以及砂體連通程度在縱向和橫向上的變化特征,其中滲透率的變化對儲層的宏觀非均質性來說是一個重要影響因素,滲透率變異系數是表征儲層滲透率非均質性的一個重要參數,也是影響油田采收率的一個重要因素,在油藏工程和地質研究中有著廣泛的應用[1-2]。目前主要有3種計算滲透率變異系數的方法,筆者對每種計算方法的計算步驟、原理和適用范圍進行了評價對比,并以東部層狀砂巖油田進入特高含水階段的7個區塊為例進行驗證和比較,為合理準確測算滲透率變異系數和選擇計算方法提供技術依據。

1 滲透率變異系數的含義

滲透率變異系數反映儲層滲透率非均質程度,表示圍繞滲透率集中趨勢的離散程度。一般來講,滲透率變異系數大于0,其值越小,表明均質性越強;其值愈大,則表明非均質性愈強[3-4]。目前有3種計算滲透率變異系數的方法。

2 統計學理論公式法

標準變異系數[5]是一組數據的變異指標與其平均指標之比,它是一個相對變異指標。變異系數有全距系數、平均差系數和標準差系數等。常用的是標準差系數,用CV表示,即標準差與均值的比率,變異系數又稱離散系數,反映單位均值上的離散程度。

變異系數的計算公式為:

式中,CV為變異系數;σk為樣品滲透率標準差,m D;ˉk為樣品滲透率平均值,m D;n為樣品數量; ki為第i個樣品的滲透率,m D,h為有效厚度,m;hi為第i個樣品的有效厚度,m。

在油田實際生產中,平均滲透率通常根據自然電位等測井曲線資料對所鉆井所遇各油層得到的滲透率,利用單井各小層有效厚度加權平均得到。

該方法的優點是適合于任何滲透率分布類型;缺點是所計算的CV值在0～∞,難于確定其非均質狀況。其改進方法是對所得結果進行數據處理,使CV值處于0～1,進而得到相對的非均質強弱狀況。

3 Dykstra-Parsons定義法

Dykstra和Parsons于1950年引入了滲透率變異系數Vk的概念[4],它是一組非一致性的統計度量數據。一般用于描述滲透率屬性,但也可延伸到處理其他巖石物性。一般認為滲透率數據是按對數正態分布的,也就是說,形成油藏巖石滲透率的地質過程,使得滲透率圍繞幾何均值分布。Dykstra和Parsons認識到了這一特性,并引入了滲透率變異的概念來表征這種分布,確定變異系數Vk需要的計算步驟如下:

1)按滲透率遞減即下降順序排列巖石樣品。

2)對每一樣品,計算滲透率大于這一樣品的厚度百分比。

3)在對數概率圖紙上,將滲透率作為對數軸,厚度百分比作為概率軸,做出點圖。

4)通過這些點畫一條最佳直線。

5)讀取厚度的比例為84.1%和50%時對應的滲透率值,記為K84.1和K50。

6)Dykstra-Parsons定義的滲透率變異系數Vk用式(4)計算:

式中,K50為巖石樣品數量累積頻率等于50%時對應的滲透率值,也稱概率平均滲透率,m D;Vk為滲透率變異系數;K84.1為巖石樣品數量累積頻率等于84.1%時對應的滲透率值,mD。

該方法的優點是可計算的Vk在0～1之間;缺點是只適合于滲透率呈對數正態分布的類型,實際應用中曲線難接近于一直線。此外,也有用巖石樣品數量百分比頻率來代替厚度百分比作為概率軸進行計算的。當前理論研究和應用中用此種方法計算滲透率變異系數的已不多,或應用滲透率級差與滲透率突進系數等類似參數代替其進行表征。

4 Lorenz系數法

基于洛倫茨曲線的基尼系數是意大利經濟學家1922年提出的定量測定收入分配差異程度的指標[6]。洛倫茨曲線是國際上公認可以用來描述社會某種收入分配差異程度的一種比較直觀的方法。Schmalz和Rahme于1950年將其引入成為一個描述儲層非均質性的參數,稱為勞倫茲系數,其取值介于完全均質系統的0和完全非均質系統的1之間,可用以下步驟計算勞倫茲系數:

1)將所有可能得到的滲透率值以遞減順序排列。

2)計算累積地層系數∑Kh(滲透率K與有效地層厚度h的乘積之和)和∑φh(孔隙度φ與有效地層厚度h的乘積之和)。

3)將這2個累積參數進行標準化,使其介于0～1之間。

4)將標準化的∑Kh和標準化的∑φh畫在笛卡爾坐標系上。5)勞倫茲系數L定義如下式:

式中,SABC為曲面三角形ABC的面積,m2;SACD為三角形ACD的面積,m2;勞倫茲系數L在0～1之間變動;0表示完全均質;1表示完全非均質。

圖1表示的是一油層流動能力的分布。完全均質系統的滲透率各處完全相等,因此標準化的∑Kh和∑φh圖為一直線。圖1表明隨滲透率的高低值差別的增大,圖像向左上角顯示更大的凹度,這說明非均質性更強。也就是說,偏離直線的嚴重程度是非均質性的量度,由此可通過計算勞倫茲系數定量描述儲層的非均質性。為了使計算簡便,更為常用的是將滲透率從大到小排隊成一序列,根據巖石樣品數量累積百分比頻率和滲透率累積百分比繪制成勞倫茲曲線進行計算。該方法優點是適合于任何滲透率分布類型,又使計算的Vk值在0～1之間。

對Wamen和Price于1961年提出的對數正態滲透率分布來說,滲透率變異系數和勞倫茲系數之間的關系,數學上可用以下2公式來表示:

1)用滲透率變異系數表示的勞倫茲系數:

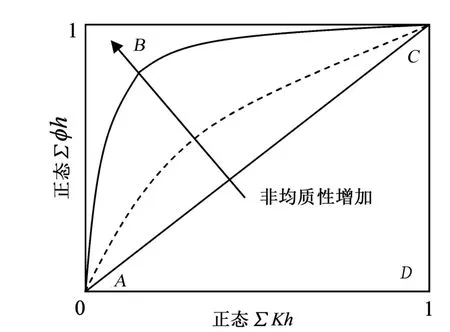
圖1 標準化的流動能力

5 實例應用

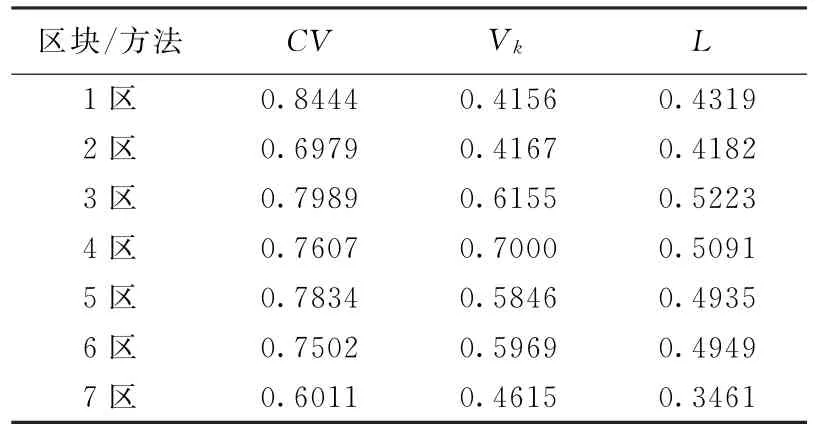
表1 東部某油田滲透率變異系數計算結果

根據以上的計算原理和方法,應用VB6.0編制了應用程序,分別應用統計學理論公式法、Dystra-Parsons法和Lorenz系數法計算了東部層狀砂巖油田7個已經進入特高含水開發階段區塊的滲透率變異系數,結果如表1所示。

地質研究表明,非均質性由強到弱的順序為:3區和4區最大,其次是5區和6區,再次是1區和2區,最小的是7區。由計算結果可以看出,其中Lorenz系數法得到的計算結果與實際認識基本相一致,Dystra-Parsons定義與統計學理論公式法與實際認識稍有差距,因此推薦應用Lorenz系數法來計算滲透率變異系數。

6 結論

1)總結了計算滲透率變異系數的3種方法——統計學理論公式法、Dykstra-Parsons定義法和lorenz系數法的計算步驟、優缺點和適用范圍。

2)實例應用表明,Lorenz系數法得到的計算結果與實際認識基本相一致,Dystra-Parsons定義與統計學理論公式法與實際認識稍有差距,推薦應用Lorenz系數法來計算滲透率變異系數。

[1]周煦迪,俞啟泰,林志芳.油層滲透率縱向非均質分布對水驅采收率的影響[J].石油勘探與開發,1997,24(1):55-58.

[2]王芳,劉德華,曹寶軍.明一西塊油藏非均質性研究[J].大慶石油地質與開發,2004,23(1):27-28.

[3]黎文清.油氣田開發地質[M].北京:石油工業出版社,1992.

[4](美)H.C.斯利德.實用油藏工程學方法[M].徐懷大譯.北京:石油工業出版社,1982.

[5]陳家鼎,鄭忠國.概率與統計[M].北京:北京大學出版社,2007.

[6]康曉東,劉德華,蔣明煊,等.洛倫茨曲線在油藏工程中的應用[J].新疆石油地質,2002,23(1):65-67.

[7]王亞婧,郭少斌.應用灰色系統理論評價松遼盆地北部葡萄花油田儲層[J].巖性油氣藏,2011,23(5):60-63.

[8]孫紅志,劉吉余.儲層綜合定量評價方法研究[J].大慶石油地質與開發,2004,23(6):8-10.

[編輯]辛長靜

TE311.2

A

1673-1409(2014)26-0084-03

2014-03-10

國家科技重大專項(2011ZX05052)。

桂東旭(1983-),男,工程師,現主要從事油田開發規劃方面的研究工作。