定時截尾樣本下兩參數指數-威布爾分布的可靠性Bayes估計
薛嬌,常勝,鄧麗
(蘭州交通大學數理與軟件工程學院,蘭州 730070)
定時截尾樣本下兩參數指數-威布爾分布的可靠性Bayes估計
薛嬌,常勝,鄧麗
(蘭州交通大學數理與軟件工程學院,蘭州 730070)
將可靠度R和失效率λ分別看成隨機變量或是關于隨機變量θ的函數;首先求出了指數-威布爾分布的可靠度和失效率的極大似然估計;然后根據參數θ的后驗密度求出可靠度和失效率的后驗密度;進一步在Entropy損失函數下求出了可靠度和失效率的Bayes估計,并給出了可靠度和失效率的E-Bayes估計;最后進行實例模擬。結果表明:Entropy損失下的Bayes估計較極大似然估計好。
指數-威布爾分布;Entropy損失函數;可靠度;失效率;極大似然估計;Bayes估計
隨著科學技術的迅速發展,在生物學、工程學、航天學和醫學等領域中,出現了一種非單調失效率的分布,例如浴缸型失效率、單峰型失效率等,其中服從浴缸型失效率分布的產品表現為在使用初期有著很高的失效率,但是隨著使用時間的延長,失效率就趨于穩定,最后由于產品的損耗,失效率又逐步增加。鑒于此種情況,Mudholkar和Srivasta[1]于1993年首次提出了指數威布爾分布EW(α,θ)。由于其具有良好的非單調失效性質,較好地解決了上述存在的問題,在研究各類壽命的數據分布時得到了廣泛的運用。例如:黃傲林,葉林軍[2]研究了指數-威布爾分布在船舶裝備故障率方面的應用;張秋華[3]運用威布爾分布研究了產品失效時間的預測。
對于失效率和可靠度估計的討論,以往都是將參數的估計取代可靠度表達式中相應位置的參數,如:王建華、夏小艷[4]研究了無失效數據情形下指數分布的貝葉斯估計的性質;李翔、韋來生[5]介紹了定數截尾情形下指數分布的參數型經驗貝葉斯(PEB)估計;劉超男[6]討論了兩參數指數威布爾分布參數的Bayes估計及其可靠性分析。但對于指數-威布爾分布的可靠性分析的文章還不多見。本文主要討論當參數a已知時,參數θ、可靠度、失效率等的極大似然估計(MLE),然后將可靠度R和失效率λ分別看成隨機變量,或者將其看成關于隨機變量θ的函數,討論其在Entropy損失下的Bayes估計以及E-Bayes估計。首先設指數-威布爾分布的分布函數為

1 指數-威布爾分布的可靠度和失效率的極大似然估計(MLE)
對式(6)兩邊分別取對數得指數-威布爾分布的似然函數的對數為對式(7)關于參數θ求導并令其為0,則有
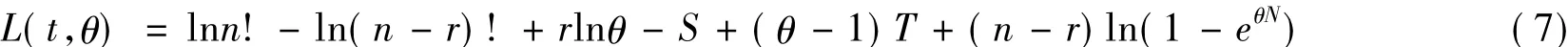
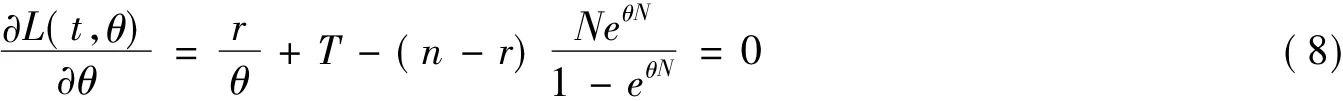

2 Entropy損失函數下指數-威布爾分布的可靠性Bayes估計
定義2[10]r.v.T服從密度函數為f(θ,t)的分布,其中θ為參數,如果δ是θ的判別空間中的一個估計,則Entropy損失函數定義為如下似然比對數的數學期望:

引理1[11]設r.v.T~f(t,θ),θ∈Θ,L(θ,δ)為某統計決策問題的損失函數,參數θ的先驗分布為G(θ),若損失函數為δ的嚴格凸函數,則該統計判決問題的Bayes解是唯一的。
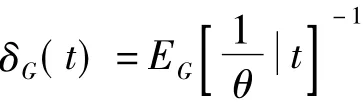
證明在Entropy損失式(14)下,決策函數δG(t)的Bayes風險為
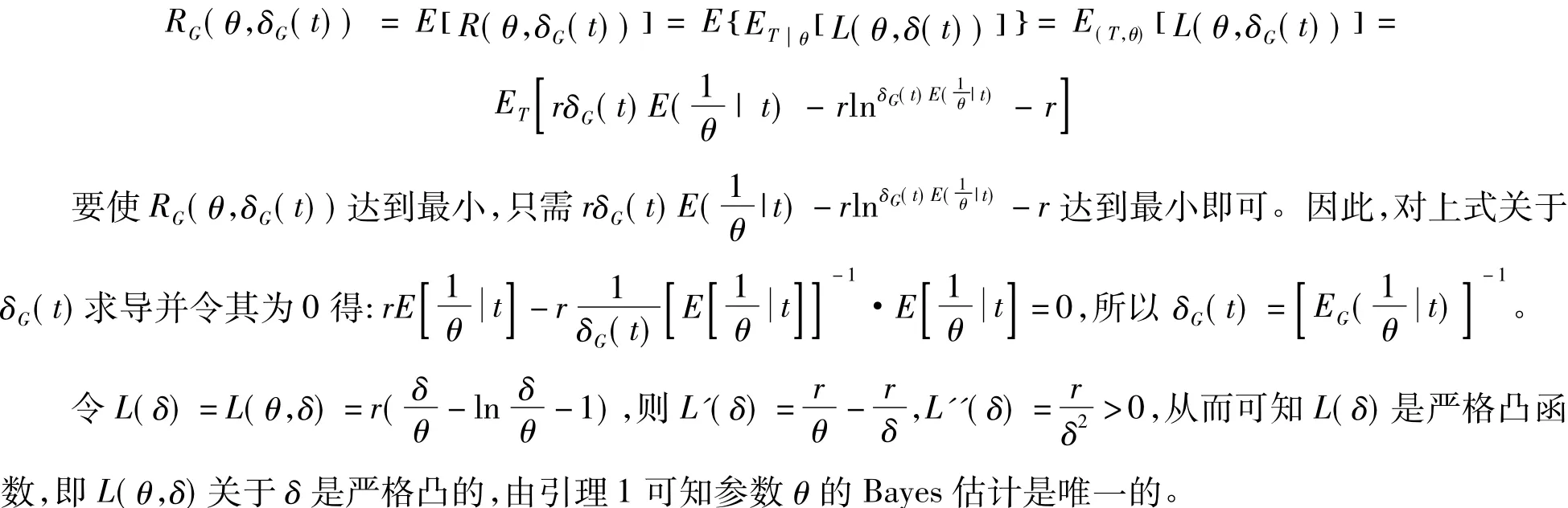



3 Entropy損失函數下指數-威布爾分布可靠性E-Bayes估計


4 實例模擬
設某產品的壽命X服從指數威布爾分布式(1),已知a0=2,θ=1.5,x=0.2,則t=0.04,即T服從指數威布爾分布式(2),且θ=1.5,t=0.04。在θ的先驗分布中,取α=1,β=2,此時求得可靠度R和失效率λ的真值為:R(t)=0.895 966,λ(t)=0.613 2。

由上述例子可知:當樣本容量較小時,Entropy損失下的Bayes估計比極大似然估計能更好地接近可靠性指標的真值;當樣本容量較大時,兩者均為可靠性指標的較好估計,但是Bayes估計較接近真值,因此Entropy損失下的Bayes估計較極大似然估計要好。
[1]Mudholkar G S,Strivastva D K.Exponentiated Weibull family for analyzing bathtub failure-rate date[J].IEEE Trans,Realiability,1993,42(2):299-302.
[2]黃傲林,葉林軍.基于威布爾分布的船舶裝備故障分析[J].船艦電子工程,2007(1):180-183.
[3]張秋華.壽命服從威布爾分布的產品失效時間的預測[J].池州學院學報,2011,25(2):7-9.
[4]王建華,夏小艷.指數分布參數多層Bayes估計及其E-Bayes估計的性質[J].應用數學,2008,20:33-36.
[5]Lindiey D V.Approximate Bayesian Methods[J].Bayesian statistics Valency,1980,20:224-245.
[6]劉超男.兩參數指數威布爾分布的參數Bayes估計及其可靠性分析[D].長沙:中南大學,2008.
[7]Rameshwar D.Gupta and Debasis Kundu.Discriminating between Gamma and Generalised Exponential Distribution[J].Journal of statistical computation and simulation,2004,274(2):107-121.
[8]茆詩松,王靜龍,濮曉龍.高等數理統計[M].2版.北京:高等教育出版社,2006.
[9]曹晉華,程侃.可靠性數學引論[M].北京:科學出版社,1986.
[10]方開泰,許建倫.統計分析[M].北京:科學出版社,1987.
[11]Yang J,Yu X.Existence of solution for a semi-linear elliptic equation in RNwith sign-changing weigh[J].Advanced Nonlinear studies,2008,8(2):401-412.
[12]劉超男,劉小慧,郭艷.熵損失函數下兩參數指數威布爾分布尺度參數的Bayes估計[J].數學理論與應用,2008,28(4): 54-57.
[13]韓明.Pascal分布參數估計[J].純粹數學與應用數學,2006,2(4):510-514.
[14]韓明.多層先驗分布的構造及其應用[J].運籌與管理,1997,6(3):31-40.
(責任編輯 劉舸)
Reliability Bayes Estimation of Two-Parameter Exponential-Weibull Distribution Based on Fixed Time Censoring Sample
XUE Jiao,CHANG Sheng,DENG Li
(School of Mathematics,Physics and Software Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China)
In this paper,reliability R and failure rate λ are regarded as random variables,or as function with a random variable θ.Firstly the Maximum Likelihood estimations of R and λ for Exponential-Weibull Distribution are solved.Then the posterior densities of R and λ are obtained according to the posterior density of parameter θ.The Bayes estimation and E-Bayes estimation of R and λ are solved under the Entropy loss function.At last,by the instance simulation,the result shows that the Bayes estimation under the Entropy loss is better than the Maximum Likelihood estimation.
Exponential-Weibull distribution;Entropy loss function;reliability;failure rate;maximum likelihood estimation;Bayes estimation
O212
A
1674-8425(2014)08-0132-08
10.3969/j.issn.1674-8425(z).2014.08.027
2014-03-18
甘肅省自然科學基金資助項目(1208RJZA111)
薛嬌(1989—),女,甘肅蘭州人,碩士研究生,主要從事應用概率與隨機分析研究。
薛嬌,常勝,鄧麗.定時截尾樣本下兩參數指數-威布爾分布的可靠性Bayes估計[J].重慶理工大學學報:自然科學版,2014(8):132-139.
format:XUE Jiao,CHANG Sheng,DENG Li.Reliability Bayes Estimation of Two-Parameter Exponential-Weibull Distribution Based on Fixed Time Censoring Sample[J].Journal of Chongqing University of Technology: Natural Science,2014(8):132-139.

