基于GARCH族的滬深300指數期現貨市場間互動關系研究

張小濤，許曉靜

(天津大學管理與經濟學部，天津 300072)

股指期貨作為一種金融衍生工具，具有重要的市場地位。它是把股票價格指數作為交易標的商品的一種期貨，也是買賣雙方根據事先約定，同意在未來某一特定時間以約定價格進行股指期貨交易的一種標準化協議［1］。2010年4月16日，滬深300股指期貨合約上市推出，這意味著我國的資本市場結束了沒有金融期貨的歷史。

由于股指期貨推出之后，資本市場結構出現了巨大的變化，基礎資產市場與衍生品市場同時存在，兩者的相互影響機制與單一基礎資產市場會有很大不同。因此只有掌握股指期貨與股票市場的風險規律，才能更好地發展我國的金融衍生品市場，并促進我國基礎資產市場的健康繁榮發展。為此，本文對滬深300指數期、現貨市場之間可能的相互引導關系及期貨市場對現貨市場的波動性影響進行了研究與討論。

1 文獻回顧

Garbade和Silber是最早涉足期貨與現貨價格之間聯動性關系探索的學者。二人在1983年通過使用動態模型的方法嘗試研究期、現貨價格在價格發現中功能的大小［3］。1987年Kawaller和Koch［4］對芝加哥商品交易(即CME)每分鐘數據進行研究，發現無論是在對不同的交易日，還是在對不同的期貨合約的檢驗之中均穩定地存在領先-滯后關系。黃玉娟［5］研究了TAIFEX期貨與其現貨和SIMEX期貨與其現貨4個市場間的領先與落后關系，發現期貨市場不具備價格發現功能，而TAIFEX期貨的價格關系明顯落后。嚴敏、巴曙松［6］運用公共因子模型等方法，研究和分析滬深300股指期、現貨市場之間的價格發現功能以及互動關系，發現兩價格之間存在著的均衡關系是長期的，而存在的雙向的Granger因果關系是短期的。1994年Gerety和 Mulherin［10］通過研究美國市場的期貨對股價指數的影響，發現變異系數沒有出現明顯的改變。Bessembinder，Hendrik等［11］在1992年發表文章分析了上世紀70年代至80年代21年間S＆P500指數期貨推出前后的情況，發現期貨市場的引入減小了現貨市場的波動性。

2 滬深300指數期、現貨市場之間的信息引導關系研究

理論上，由于股價指數期貨合約與現貨指數均反映了基礎股票的價值，因此如果存在瞬時套利，那么指數期貨應既不先行、也不滯后于現貨指數。但由于股價指數期貨的理論價格與實際價格的不一致，以及期、現貨市場在結構與制度方面存在許多差異，使得兩市場對資訊的反應速度并不同步，因為可能會產生領先滯后關系［2］。基于Granger因果檢驗等方法的實證結果表明:一般來說，期貨市場要先行于現貨市場，現貨市場對期貨市場不存在或有時存在很小的反饋。

2.1 樣本數據說明

本研究以我國的滬深300指數現貨及期貨數據作為研究樣本對象，資料范圍為CSI300股指期貨上市日2010年4月16日至2010年10月29日的5秒鐘高頻價格序列，2個市場各取得371 520筆同時點的價格序列。

為了保證數據的穩定性和更好地表現統計性質，本文使用價格的對數差分收益率作為研究樣本，形式如下:

Rt=［ln(Pt)-ln(Pt-1)］×100%

2.2 實證分析

2.2.1 收益序列的平穩性檢驗

由表1可以看出滬深300指數現貨和其期貨的對數收益率序列都滿足平穩性要求，所以不必再進行協整檢驗，下面可以直接對這2個時間序列做Granger因果關系檢驗。

表1 兩市場指數收益率序列的ADF檢驗

2.2.2 Granger因果關系檢驗

當序列的滯后期大于某個階數的時候，AIC與SBIC準則的測試結果所呈現的遞減程度明顯下降，所以可以根據這項原則來確定VAR模型的滯后階數。通過表2使用AIC最小值第25期作為最優滯后期。

由表3可以看出:期貨的收益率和其現貨的收益率之間互為Granger原因，說明這兩個市場之間是有相互引導關系的。這里需要注意的是:“Granger因果關系”并不意味著一個變量的變化就是另一個變量變化的真正原因，這里的因果關系僅表示序列運動在時期上的先后次序［7］。真正的因果關系非常復雜，涉及很多問題，一般很難用統計方法直接檢驗得出結論。

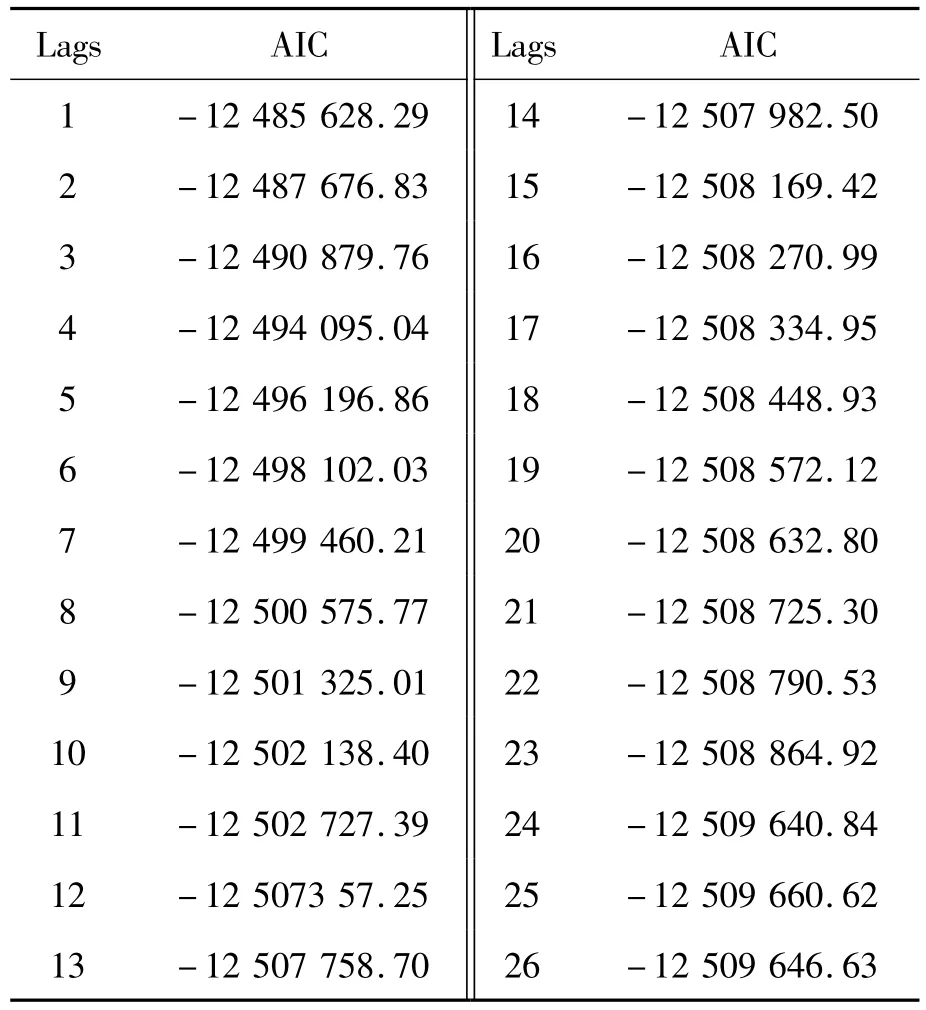
表2 模型最適階數的AIC測試

表3 對數收益率Granger因果關系檢驗

3 滬深300指數期貨市場對其現貨市場的波動性影響

股票的現貨市場在波動大小、流動快慢和成分股溢價程度等方面很有可能受到來自股指期貨推出上市的影響，且以波動性大小變化尤甚。波動性是市場價格對到達信息的反應從而引起的波動程度，是用來度量市場風險的常用指標［8］。波動性作為金融市場最為重要的特征之一，對它的研究一直以來都是金融領域研究的熱點［9］。本部分將使用較新的期貨、現貨數據研究2個市場間波動率的持續性、不對稱性，進一步分析中國股指期貨對于現貨價格發現不確定性的影響。

3.1 樣本數據說明

本部分資料為2010年1月4日至2010年10月29日滬深300指數現貨的5秒鐘高頻對數收益率序列，共計567 359個數據。將股指期貨引進前，即2010年1月4日至CSI300股指期貨上市日前一天的數據作為一區間;將股指期貨引進后，即CSI300股指期貨上市日至2010年10月29日的數據作為二區間，以及CSI300股指期貨上市日至2010年10月29日滬深300指數期貨的5秒鐘高頻數收益率序列。

3.2 實證分析

3.2.1 單位根檢驗

本文在使用時間序列模型進行實證之前，須先對滬深300指數的現貨收益率做平穩性檢驗。現貨區間二及期貨的平穩性檢驗已在上文中做過說明，兩者均平穩。現對現貨總體和現貨區間一做平穩性檢驗，結果見表4、5，證明序列均是平穩序列，可對其建立時間序列模型。

表4 現貨總體的ADF檢驗

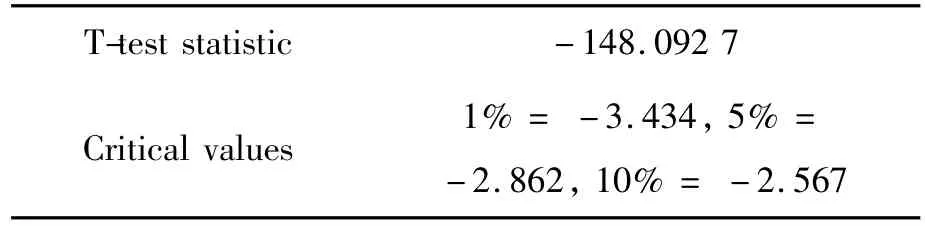
表5 現貨區間一的ADF檢驗

3.2.2 建立ARMA模型

以AIC信息準則值作為標準，對全體收益率序列進行ARMA模型的定階。結果顯示:ARMA(2，2)對應的AIC值最小，對收益率序列建立ARMA(2，2)模型比較合適。表6給出了該模型的參數估計。

3.2.3 ARCH效應檢驗

在對數據進行GARCH模型分析之前，要對已經建立均值方程后的殘差進行檢驗，觀察它是否存在有ARCH效應，根據檢驗結果判斷該類模型是否適用于特定數據。下面對文中經過ARMA(2，2)模型擬合后得到的方程殘差進行ARCH效應的檢驗。

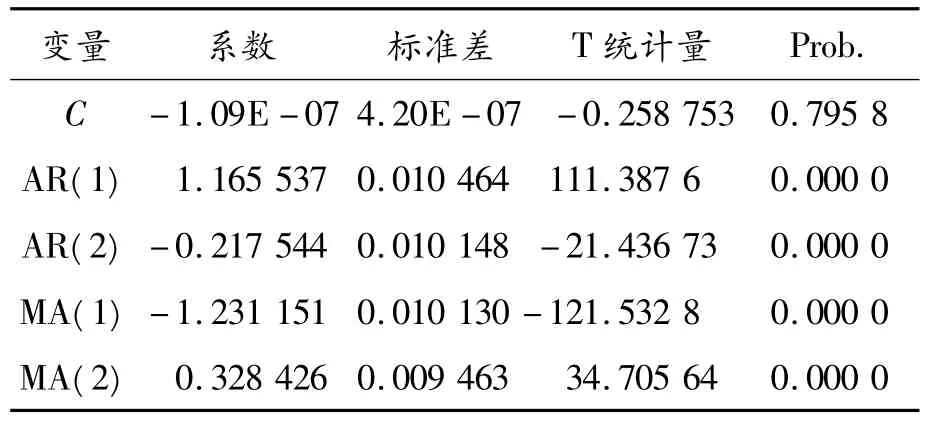
表6 ARMA(2，2)模型參數估計結果

表7的結果表明:數據在1%的概率下存在ARCH效應，可以對其建立ARCH模型族。

表7 ARCH-LM檢驗

3.2.4 波動性的持續性檢驗

研究者發現在股票報酬率產生的過程中，報酬率的波動性與時間關聯，且其非條件殘差會表現出尖峰厚尾的統計特性。GARCH模型是描述股價報酬數據行為日數據的最適當的模型之一。1992年Bollerslev在其文獻中證實，在描述大多數時間數列的波動性的過程中，采用GARCH(1，1)模型就可以獲得不錯的表現和很好的擬合。因此，在上文基礎上對全體收益率序列建立GARCH(1，1)模型。估計結果見表8。

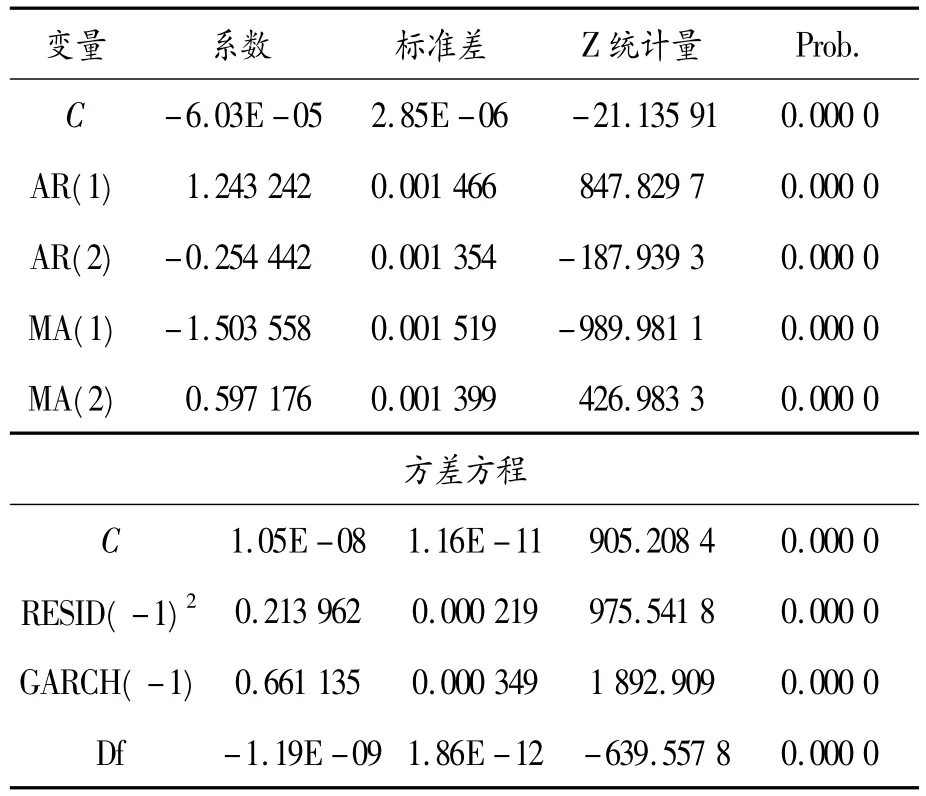
表8 GARCH模型輸出結果均值方程

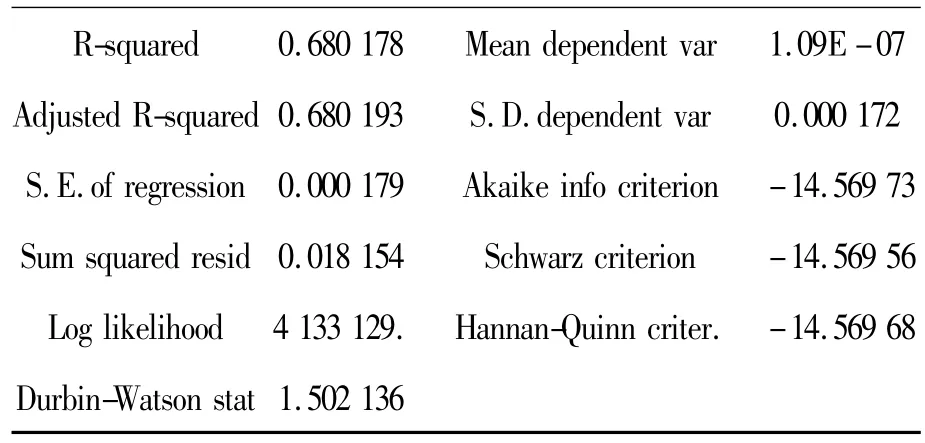
續表

經檢驗模型擬合后殘差不存在自相關和偏相關，表9給出了ARCH-LM檢驗結果。

表9 對殘差進行ARCH-LM檢驗

經檢測后可見，殘差已不存在arch效應。這說明 ARMA(2，2)-GARCH(1，1)模型可以充分擬合CSI300指數收益率時間序列。虛擬變量的估計結果顯著，證明股指期貨的引入對現貨市場的波動性產生了影響。從 df的系數來分析，CSI300指數期貨的推出對其現貨市場的波動性產生了減緩的作用。

同理，對現貨區間一和現貨區間二建立GARCH(1，1)模型，得到方差方程各變量的系數，結果見表10。

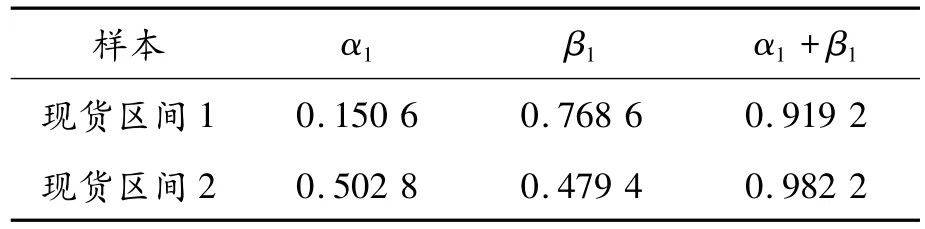
表10 GARCH模型系數結果

從表10可以看出:在期貨合約被引入之前和之后的樣本子期間中，作為反應新信息沖擊效果的系數α1和作為反應沖擊持續性效果的系數β1在不同期間的表現。期貨合約開放前，系數α1為0.150 6;而在開放之后的子期間2，α1系數增大為0.502 8。這代表在期貨合約推出之后，新信息所反映的沖擊效果確實有所增加。新信息或市場干擾(innovation)對未來波動性的沖擊程度較大。

另外，就β1系數而言，它可以被看成是沖擊干擾持續性的一個代理變量。在期貨商品引入前后，模型所表現的β1系數分別為0.768 6和0.479 4，說明在期貨合約開放交易之后，舊信息對市場波動性沖擊的持續性效果減弱了。

3.2.5 波動率不對稱性的檢驗

用EGARCH和TGARCH對滬深300指數現貨進行檢驗，結果見表11。

表11 現貨收益率數據TGARCH和EGARCH的參數

從表11可以看出:表示引入期貨市場因素的變量的系數δ具有統計顯著性，表明在引入指數期貨后，其現貨市場的波動性受到影響，發生了顯著變化。系數γ也具有統計顯著性，表明我國股市具有杠桿效應，因為數據顯示股價對利空信息的反應程度大于對利好信息的反應程度。

4 結束語

在信息傳遞方面，CSI300指數期貨收益率與其現貨收益率之間互為Granger原因，存在相互引導關系。

在波動性的持續性方面，通過實證得出CSI300指數期貨的加入加快了其現貨市場中新信息的傳遞速度，從而使得市場信息更快地轉換為未來方差。在期貨合約開放交易之后，市場波動性沖擊的持續性受舊信息影響的效果變弱，即波動性干擾的持續性效果變化變小。所以說CSI300指數期貨的交易在一定程度上提高了現貨市場的效率，但對現貨市場波動性的持續性方面影響減弱。

最后，在波動性的不對稱性方面，市場確實存在有杠桿效應，CSI300指數期貨的交易使其現貨市場波動性的不對稱性增加。

［1］楊星.股指期貨［M］.廣州:廣東經濟出版社，2002:629.

［2］謝凱丞.臺灣類股指數期貨與現貨領先落后關系之實證研究［D］.臺南:臺灣成功大學.

［3］Garbade K D，Silber W L.Price movements and price discovery in futures and cash markets［J］.The Review of Economics and Statistics，1983，65(2):289-297.

［4］Kawaller I G，Koch P D，Koch T W.The temporal price relationship between S＆P 500 futures and the S＆P 500 index［J］.The Journal of Finance，1987，42(5):1309-1329.

［5］黃玉娟，黃珮鈴.臺灣股價指數現貨與期貨價格領先落后關系之探討——以TAIFEX與SGX-DT為例［J］.輔仁管理論壇，2004，11(1):125-152.

［6］嚴敏，巴曙松，吳博.我國股指期貨市場的價格發現與波動溢出效應［J］.系統工程，2009，27(10):34-38.

［7］克里斯·布魯克斯.金融計量經濟學導論［M］.成都:西南財經大學出版社，2005:316-317.

［8］姚興濤.中國股指期貨市場概論［M］.北京:北京大學出版社，2001:3-8.

［9］徐國祥，吳澤智.金融指數產品創新及其風險控制研究［M］.上海:上海財經大學出版社，2005:38-40.

［10］Gerety M S，Mulherin J H.Price formation on stock exchanges:The evolution of trading within the day［J］.Review of Financial Studies，1994，7(3):609-629.

［11］Bessembinder H，Seguin P J.Futures-Trading Activity and Stock Price Volatility［J］.The Journal of Finance，1992，47(5):2015-2034.