秩虧自由網序貫平差及各模型比較分析
陸建華,徐克成
(1.蘇州市測繪院有限責任公司,江蘇 蘇州 215000;2.中國礦業大學環境與測繪學院,江蘇 徐州 221116)
1 引 言
若在原來控制網的基礎上進行擴建或對舊網進行復測,可按序貫平差原理進行平差[1],它可充分利用前期平差結果與當前觀測樣本,無需存儲歷史觀測數據,無需求大矩陣逆就能獲得與整體平差相同的最優解,具有計算公式簡潔、規律性強、計算量小的特點[2]。但如果前期平差為秩虧自由網平差結果,則其權逆陣不存在,問題就變為秩虧自由網的序貫平差。
本文對第一次平差后得到虛擬觀測值的權逆陣進行了適當變換,得到了其權陣PX,的計算通式,解決了秩虧問題,可為變形監測等分期完成的測量工程提供可取的數據處理方法。然后,詳細闡述了重心基準自由網平差、擬穩平差模型,并通過實例計算對其平差結果進行比較分析,得出了相關結論。
2 序貫平差基本原理
序慣平差是指將觀測值分成兩組或多組,按組的順序分別做相關間接平差,從而使其達到與兩期網一起做整體平差同樣的效果。分組后法方程階數降低,減輕了計算強度,以下以分兩組為例介紹其基本原理及平差過程[3]。
上式中,Li為觀測值,B 為系數陣,d、l 為構成函數關系式的常數項。
按間接平差原理,先對第一組誤差方程進行第一次平差,其法方程為:

可解得第一次平差后未知參數和觀測值的改正數,分別為:
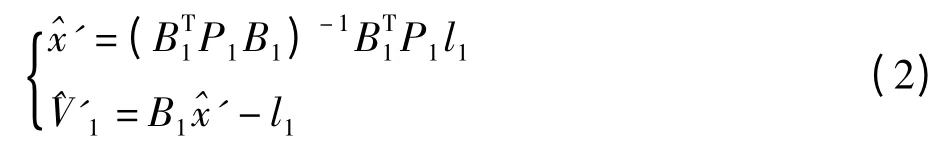
再對第二組誤差方程做第二次平差,此時將第一次平差后得到的參數為初值)作為虛擬觀測值參與平差,其權陣為。誤差方程為:

聯合第二組誤差方程,可得法方程:

即:

可解得第二次平差后未知參數和觀測值的改正數,分別為:
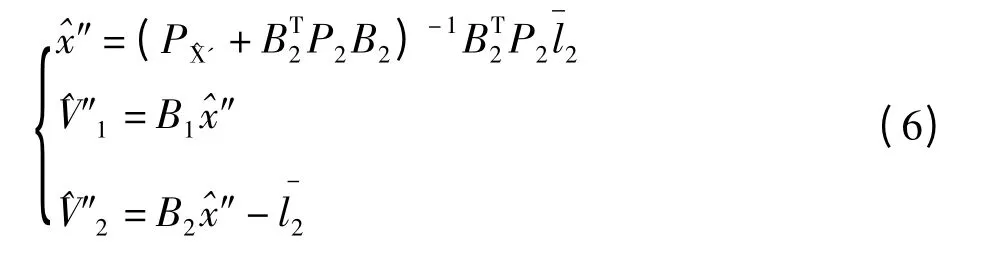
最后平差值為:

3 秩虧自由網序貫平差模型
當監測網中沒有必要的起算數據時,應用序貫平差進行數據處理得到的前期平差結果作為虛擬觀測值的權陣不存在,變為秩虧自由網的序貫平差問題。以下進行了適當變換,給出了虛擬觀測值權陣的計算方法,解決了秩虧問題。
3.1 權逆陣計算
當網中存在秩虧時,為獲得未知參數的唯一解可給定加權基準約束條件:,因此平差模型變為:

將S 標準化為G,使滿足:GTPxG=E
則可解得:

則按協因數傳播定律,有:

由于平差結束后QX'X'可求出,所以整理得:

即:
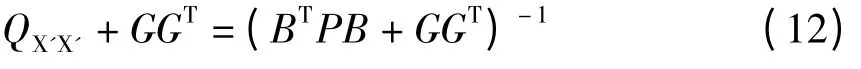
兩邊求逆并移項可得:
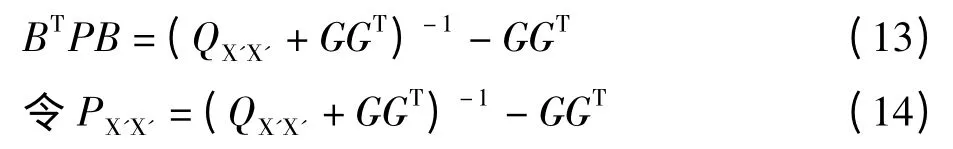
可以容易的證明,當將第一期平差結果作為虛擬觀測值,并按上式給出其權陣,與新增觀測值一起平差,可以得到與整體平差一樣的結果。所以式子:
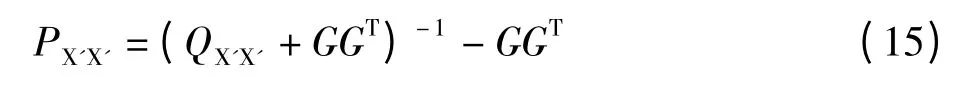
可以作為秩虧自由網序貫平差虛擬觀測值權陣的計算通式。
當虛擬觀測值的權陣確定以后,按上節中序貫平差原理進行第二次平差,即可計算得到觀測值及參數的改正數,解決了秩虧問題。
3.2 平差模型
附加基準條件的秩虧自由網平差,當選擇的基準不同時其平差模型也不同,以下介紹基于重心基準的秩虧自由網平差和擬穩平差模型[4]。
(1)重心基準秩虧自由網平差
采用重心基準,其基準權為單位陣,Px=E,又稱為普通秩虧自由網平差[5]。
由式(8)可得平差模型變為:

由式(9)、式(10)得模型的參數估計為:

(2)擬穩平差
其基準權為:

基準約束為:

則擬穩平差的基準約束條件為:

所以,擬穩平差的平差模型為:

由式(9)、式(10)得擬穩平差模型的參數估計為:

擬穩平差模型是將全部網點分為兩部分X1、X2,X2是擬穩點組成的參數,基準約束條件式(20)中僅包含X2,所以擬穩平差實質是擬穩點組的重心基準[6]。
4 算例分析
算例一:設有水準網如圖1 所示,一期觀測了h1,h4,h5,平差后高程的協因數陣為:

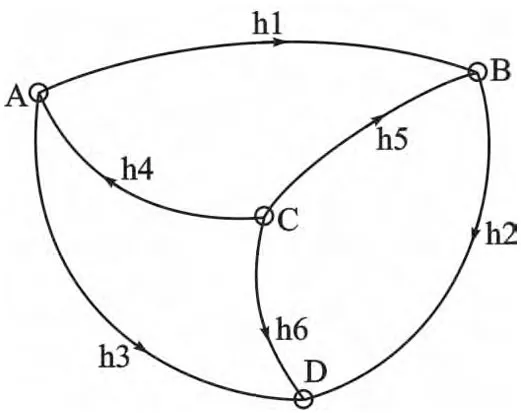
圖1 實例一觀測水準網示意圖
觀測高差、距離和各待定點高程近似值如表1 所示。
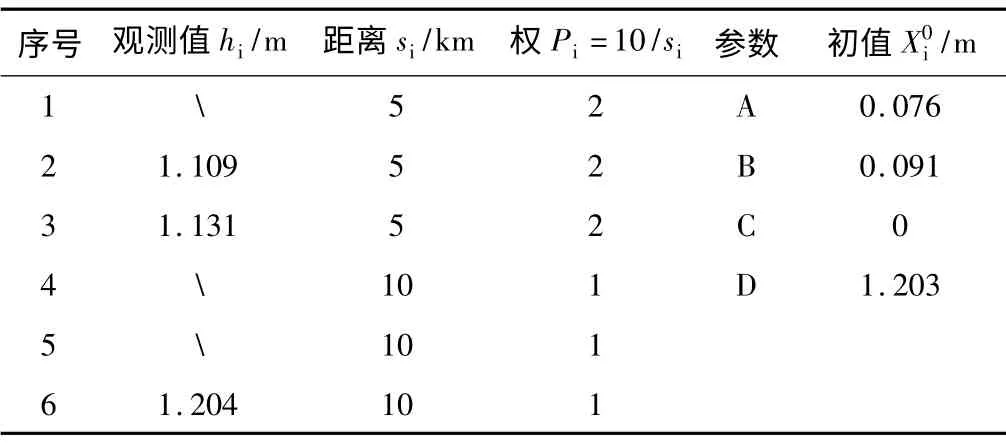
觀測高差、距離和待定點近似值 表1
當選擇重力基準秩虧自由網平差模型時,根據算例第一期水準網有3 個未知點,則:
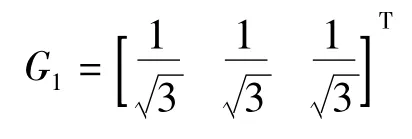
由式(14)可得:
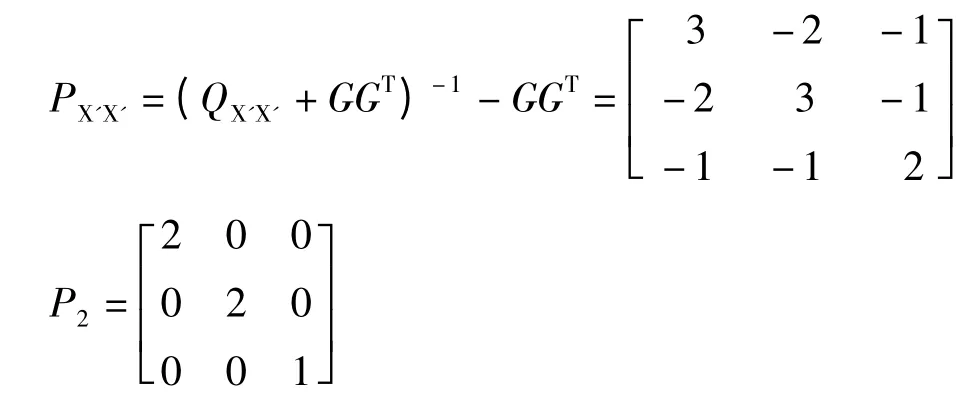
第二期觀測誤差方程式為:

由式(6)可得:
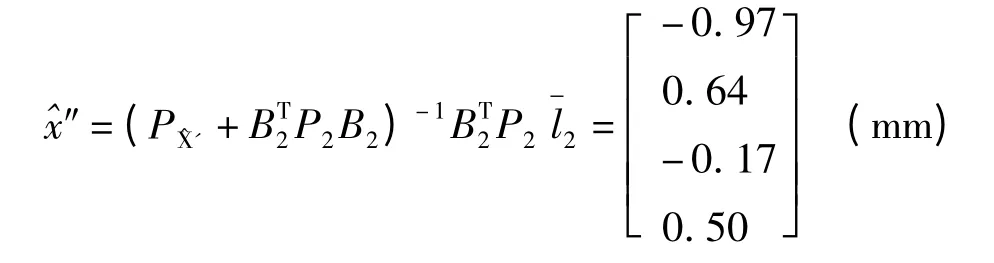
由式(7)可得:

算例二:設有水準網如圖2 所示,其中各觀測高差、距離和各待定點高程如表2 所示,分別進行以F 點為固定點的經典自由網平差、以重心基準的秩虧自由網平差及以A、B、E、F 為擬穩點的擬穩平差。

圖2 實例二觀測水準網示意圖
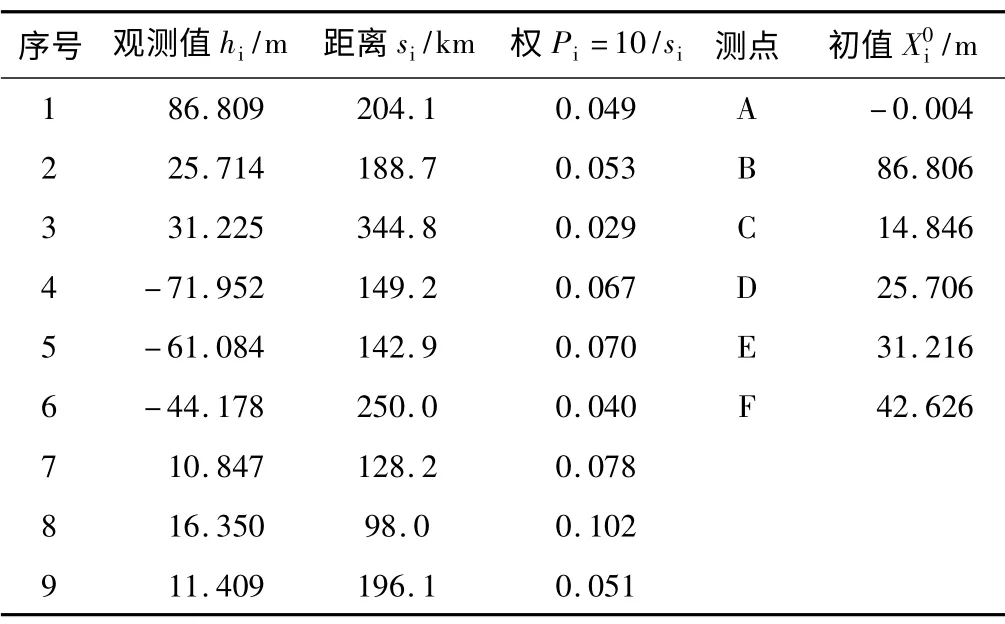
觀測高差、距離和待定點近似值 表2
根據算例可得誤差方程為:

以重心基準進行自由網平差,Px=E 水準網有6點,則:

以A、B、E、F 為擬穩點進行擬穩平差時,Px=diag[1 1 0 0 1 1],則:

根據式(17)、式(22),應用matlab 7.0 編程實現,經演算得到結果如表3 所示:

觀測高差、距離和待定點近似值 表3
未知參數估值的協因數陣為:

對結果進行分析,可知:經典自由網平差、重心基準自由網平差和擬穩平差所得觀測值改正數相同,且均滿足VTPV=min;重心基準自由網平差,tr(QX'X')=min;擬穩平差。
5 結 論
(2)經典自由網平差、重心基準自由網平差和擬穩平差所得觀測值改正數相同,且均滿足VTPV=min。
(4)擬穩平差滿足
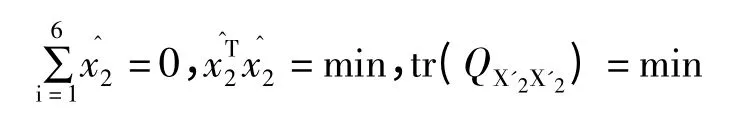
[1]張書畢,單世坤,王堅.秩虧自由網逐次平差及其應用[J].測繪通報,2001,8:26~28.
[2]曾安敏,張麗萍.多種序貫平差方法的比較[J].大地測量與地球動力學,2007,27(2):84~87.
[3]葛永慧.測量平差[M].徐州:中國礦業大學出版社,2005.
[4]崔希璋等.廣義測量平差[M].武漢:武漢大學出版社,2009.
[5]邱飛廷,董坤烽,李朝光等.帶基準權的秩虧自由網平差及其應用[J].江西科學,2010,28(5):666~668.
[6]萬斐,陳艷艷.擬穩平差在測量數據處理中的應用[J].地理空間信息,2008,6(6).

