改進元胞多目標遺傳算法在機床主軸優化中的應用*

張 屹，萬興余，鄭小東，余竹瑪

(三峽大學 水電機械設備設計與維護湖北省重點實驗室，湖北 宜昌 443002)

0 引言

機床主軸是機床的核心部件，其作用是帶動刀具旋轉，直接參與高速切削加工。機床主軸的好壞對機床的加工精度，表面質量和生產率影響很大。國內外不少科研人員對機床主軸進行了一系列科學研究，但大多數都是集中在提高主軸的某一個性能，例如，減少變形，提高剛度或者是減小振動或者是減輕重量。然而，在實際工程應用中，往往是要求多個性能盡量同時達到最優，例如要求質量最小的同時剛度要盡量大，這也就形成了多目標優化問題。近年來，出現了一些比較好的多目標優化算法，如NSGA-II［1］、SPEA2［2］、PAES［3］和MOCell［4］等。經過測試函數的比較，發現MOCell 在解決兩目標優化問題時取得了比其他幾個算法略好的性能［4］。但是，測試函數［5］是人為構造出來對算法性能進行測試的一類問題，往往與實際工程問題有較大差別，例如個體編碼，約束處理，遺傳參數的選取等都不盡相同，當要把一個算法應用到實際問題中時，不得不做相應的修改。本文針對機床主軸的參數優化設計問題，在MOCell 算法的基礎上采用實數與整數混合編碼和NSGA-II 的約束處理機制，基于正交試驗理論對MOCell 算法的參數進行優化，利用優化后的MOCell 算法來求解機床主軸優化問題，獲得其Pareto 前端，為MOCell 算法求解同時具有實數決策變量和整數決策變量的實際工程問題提供一定的借鑒作用。

1 機床主軸優化模型

機床主軸的示意圖［6］如圖1 所示。其中da為主軸懸伸段直徑，db為主軸左右支撐間的軸徑，l為支撐間的跨距，a為主軸懸臂端的長度，d0為主軸內孔直徑。

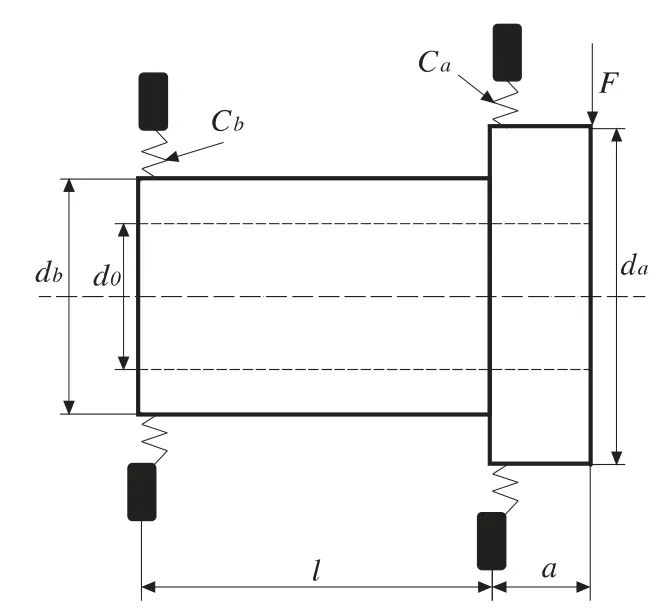
圖1 機床主軸示意圖

根據材料力學和機械設計的知識，建立的數學模型如下:

主軸體積(mm3):

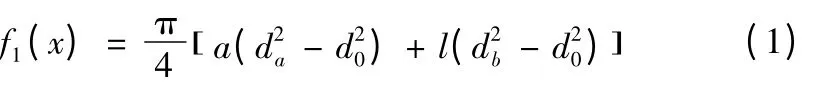
靜力F 作用下的撓度(mm):

其中，Ia和Ib分別為主軸懸伸段和左右軸承支撐段的轉動慣量。

Ca和Cb分別為右邊支撐軸承和左邊支撐軸承的剛度。

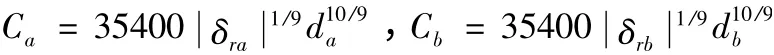
這里，δra和δrb分別為軸承的預載荷。

邊界約束條件:

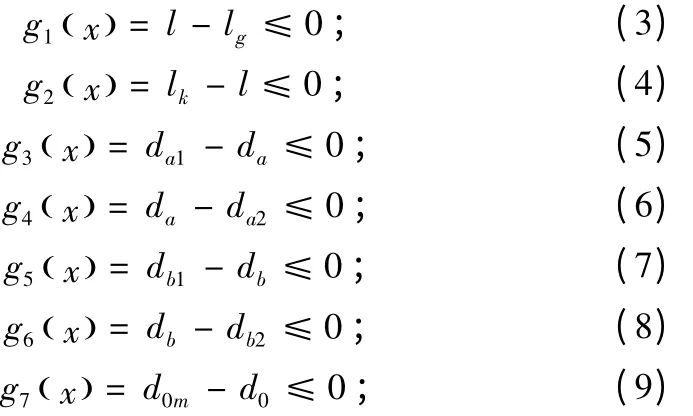
工程設計上對各個直徑的比例要求:

機床主軸端部的最大徑向跳動約束:

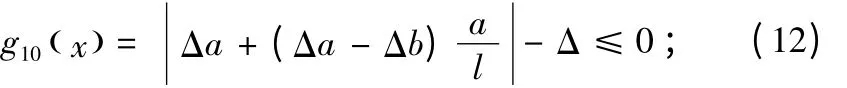
其中，Δa和Δb分別為右端和左端軸承的徑向跳動，Δ 為允許的最大徑向跳動。

這個優化問題的決策變量是l、d0、da、db，其中da和db是離散變量，da只能取{80，85，90，95}中的某一個值，db只能取{75，80，85，90}中的某一個值。以上數學模型中的常量［7］給定如下:

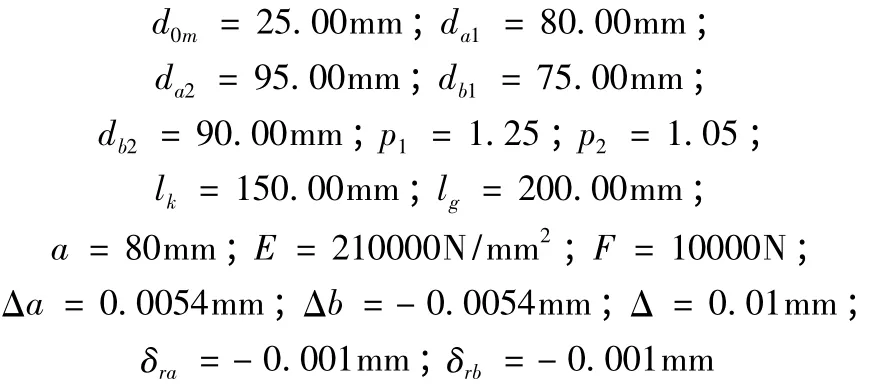
2 算法設計

2.1 算法介紹

多目標元胞遺傳算法(MOCell)是在元胞遺傳算法(cGA)［8］的基礎上發展而來的，與cGA 相比，MOCell 的改進在于加入了外部文檔，里面存放的是到目前為止算法找到的非支配解，并且引入了反饋機制，即在算法的每一次迭代完成后都選擇出一定數量的個體來隨機替換掉種群中相等數量的個體。加入外部文檔的同時，對外部文檔的容量大小做了限制，當找到的非支配解數量超出容量限制時，就會使用擁擠機制來對個體進行篩選，保留擁擠距離大的個體(使用的策略與NSGA-II 中的相同)，這種方法能夠保持解集分布的均勻性，有利于得到分布均勻的Pareto 前端。引入反饋機制后，能夠充分利用已經找到的較優解來引導種群的進化，有利于提高算法的收斂性能。MOCell 算法的偽代碼如表1 所示。

表1 MOCell 算法偽代碼

2.2 個體編碼設計

在機床主軸優化這個實際問題中，問題的決策變量是l、d0、da、db，其中da和db是離散變量，da只能取{80，85，90，95}中的某一個值，db只能取{75，80，85，90}中的某一個值。因此，不宜使用二進制編碼方法。本文采用的方法是將l、d0兩個決策變量使用實數編碼，組成編碼串的前半部分，da、db兩個決策變量使用整數編碼，組成編碼串的后半部分。由于每個編碼串對應位置的編碼方式相同，因此可以采用單點交叉。

2.3 變異算子設計

個體的編碼串是由實數和整數混合編碼構成，無論是采用多項式變異還是模擬二進制變異都不能保證編碼串的整數編碼部分仍為整數。基于此，本文采取的方法如下:

步驟1，將個體編碼串的實數編碼部分提取出來作為前半部分，將個體編碼串的整數編碼部分提取出來作為后半部分;

步驟2，對前半部分進行模擬二進制變異(SBX)［9］;

步驟3，對后半部分進行變異。具體做法是，首先分別定義兩個數組，將{80，85，90，95}和{75，80，85，90}分別存入其中，然后編寫一個0 到3 范圍內的隨機整數生成函數，每次變異的時候調用這個函數產生一個0 到3 范圍內的整數，然后以這個整數為索引找到相應數組里面的具體值;

步驟4，前半部分和后半部分的變異都完成后，將得到的結果重新組合起來構成一個新的編碼串，即為得到的變異個體。

2.4 約束處理

為了對問題的約束條件進行處理，采用的方法是當兩個個體進行比較的時候，對它們的約束進行檢查。如果兩個個體都沒有違反約束，即它們都是可行解，則直接使用Pareto 支配關系選出較優者;如果一個沒有違反約束，而另外一個違反了約束，則沒有違反約束的個體較優;如果兩個個體都違反了約束，則違反約束少的個體較優。

2.5 正交設計

在遺傳算法中，有較多的參數需要進行設置，例如種群大小、交叉概率、變異概率等，遺傳參數的選取對算法的性能有較大影響，太差的參數設置甚至會使算法無法收斂。在MOCell 算法中，需要進行設置的參數包括種群大小、鄰居大小、反饋個體數量、交叉概率和變異概率。到目前為止，這些參數的設置還沒有一個準確的理論依據，大多數情況下都是憑借經驗選取的，有一定的盲目性，而正交試驗法能夠提供一定的指導作用。

“正交試驗法”是研究與處理多因素試驗的一種科學方法［10］，它是在實際經驗與理論認識的基礎上，利用一種排列整齊的規格化表——“正交表”來安排試驗。由于正交表具有均衡分散，整齊可比的特點，能在考查的范圍內，選出代表性強的少數試驗條件做到均衡抽樣。由于是均衡抽樣，能夠通過少數的試驗次數找到一個較優的試驗參數設置。利用這一特點，找到一個最優參數組合來配置MOCell 算法，求解機床主軸優化模型。

用MOCell 算法求解機床主軸優化模型時，有5 個主要因素需要考慮，即種群大小、鄰居大小、反饋個體數量、交叉概率和變異概率。其中，種群取較大的值時，多樣性會得到一定的提高，但計算消耗會增大，因此一般取為100 到200 之間，交叉概率一般取0.6 到1之間，變異概率一般取0.1 到0.25 之間。為了使試驗能夠廣泛地覆蓋整個可能組合，同時試驗次數又不至于太多，每個因素取4 個水平。因此選擇正交表L16(45)，即5 因素4 水平16 次試驗。確定因素水平表如表2 所示，其中，由于使用的是正方形環形拓撲結構的種群，因此種群大小都是平方數。

表2 因素-水平表

2.6 確定評判指標

對算法結果進行評判時，需要一個可靠的評價指標，對算法來說，性能的好壞主要表現在收斂性和分布性兩個方面，評價收斂性的指標有GD(世代距離)，評價分布性的指標有Spread(分布指標)，另外還有對收斂性和分布性進行綜合評價的指標HV(超體積)［11］。本文選用HV 指標對算法結果做綜合評判，此指標的值越大越好。

3 問題求解及結果分析

按照正交表L16(45)和因素-水平表確定試驗方案，應用java 編程語言編程進行求解試驗，算法的終止條件是25000 次適應度評估，外部文檔的大小取為100。為了盡量減少隨機誤差，每個方案都獨立運行20 次，然后將得到的20 組試驗結果取平均值，試驗方案和結果如表3 所示。

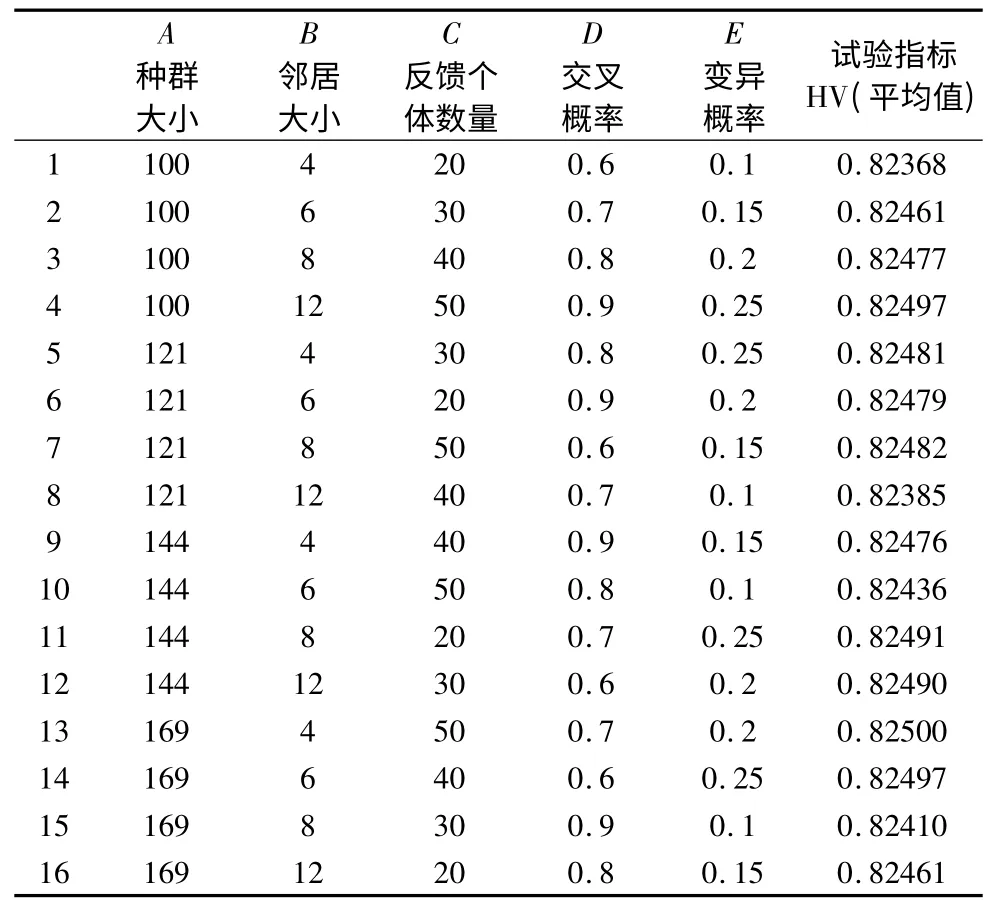
表3 試驗方案及結果表

圖2 指標-因素圖

為了更直觀的看出各因素水平的差異，用因素的水平作橫坐標，指標HV 作縱坐標，做出指標-因素關系圖，如圖2 所示。在這個實際問題中，我們需要得到最大的HV 值，因此從圖2 中可以很直觀的看出A因素取A3，B因素取B2，C因素取C4，D因素取D4，E因素取E4。從而，可以得出此問題的最佳參數配置是A3B2C4D4E4，即種群大小取144，鄰居大小取6，反饋個數取50，交叉概率取0.9，變異概率取0.25，按照這種參數配置，重新獨立運行程序10 次，得到HV 的平均值是0.83539。從HV 指標來看，與表3 中的結果相比，MOCell 算法的性能確實有所提高。需要說明的是，HV 的數值經過歸一化處理，其數值的微小變化會對算法的收斂性和分布性產生較大影響，求出的機床優化模型Pareto 前端如圖3 所示。

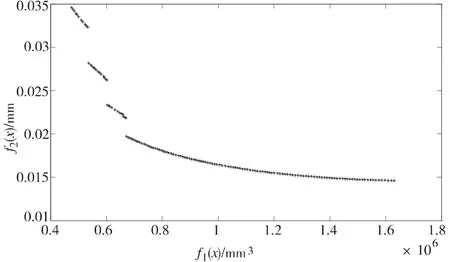
圖3 機床優化模型的Pareto 前端

對于多目標優化問題，我們的主要任務就是找到盡可能接近真實Pareto 前端并且分布盡量均勻和寬廣的解集，讓決策者根據自己的偏好來選擇最合適的解。從圖3 可以看出，機床主軸優化模型的Pareto 前端是不連續的，如果使用傳統的數學方法來求解會比較困難，但是，使用MOCell 算法能夠找到分布非常均勻的Pareto 前端，有利于決策者做出決策。

4 結束語

本文以機床主軸優化設計問題為研究對象，以主軸體積最小和撓度最小為目標，以主軸懸伸段直徑、主軸左右支撐間的軸徑、支撐間的跨距和主軸內孔直徑為決策變量，建立了多目標優化設計數學模型。在對模型進行求解時引入了多目標元胞遺傳算法(MOCell)，在MOCell 的基本框架下，結合實際問題的特點，采用了實數-整數混合編碼，設計了新的變異方法。為了避免設置遺傳參數時的盲目性，使種群大小、鄰居大小、反饋個體數量、交叉概率和變異概率的參數設置更加合理，引入了正交試驗的思想，經過程序運行試驗，找到了較優的參數組合。將通過正交試驗獲得的參數配置應用到MOCell 算法中對模型進行求解，得到了分布較為均勻的Pareto 前端，有利于決策者根據實際情況做出合適的選擇。本文為用MOCell 算法解決實際工程問題做出了嘗試，也為其他工程設計人員解決具有整數決策變量和實數決策變量問題時提供了一定的借鑒作用。

［1］Deb K，Pratap A，Agarwal S，et al. A fast and elitist multiobjective genetic algorithm:NSGA-II［J］. Evolutionary Computation，IEEE Transactions on， 2002， 6 (2 ):182 -197.

［2］Zitzler E，Thiele L. Multi-objective evolutionary algorithms:A comparative case study and the strength Pareto approach.IEEE Transactions on Evolutionary Computation，1999，3(4):257 -271.

［3］雷德明，嚴新平. 多目標智能優化算法及其應用［M］.北京:科學出版社，2009.

［4］Nebro Antonio J，Durillo Juan J，Luna Francisco，Dorronsoro Bernabe，Alba Enrique. MOCell:A cellular genetic algorithm for multiobjective optimization［J］. International Journal of intelligent systems，2009，24(7):726 -746.

［5］Dorronsoro B，Bouvry P. Cellular genetic algorithms without additional parameters［J］. The Journal of Supercomputing，2013，63(3):816 -835.

［6］Ali Riza，Yildiz. A novel hybrid immune algorithm for global optimization in design and manufacturing［J］. Robotics and Computer-Integrated Manufacturing，2009，25 (2):261 -270.

［7］Coello CAC. An empirical study of evolutionary techniques for multiobjective optimization in engineering design［D］.New Orleans:Department of Computer Science，Tulane University，1996.

［8］Alba E，Dorronsoro B. The exploration/ exploitation tradeoff in dynamic cellular genetic algorithms［J］. Evolutionary Computation，IEEE Transactions on， 2005， 9 (2 ):126 -142.

［9］Deb K，Agrawal R B. Simulated binary crossover for continuous search space［J］. Complex Systems，1995，9(2):115 -148.

［10］何為，薛衛東，唐斌. 優化試驗設計方法及數據分析［M］.北京:化學工業出版社，2012.

［11］Zitzler E，Thiele L. Multiobjective evolutionary algorithms:a comparative case study and the strength Pareto approach［J］. Evolutionary Computation，1999，3(4):257 -271.