龍門剪切機料箱的結構分析與優化*
賈 蕭,章泳健,戴國洪,陳慶樟
(1.常熟理工學院 機械工程學院,江蘇 常熟 215500;2. 蘇州大學 機電工程學院,江蘇 蘇州215000)
0 引言
龍門剪切機是液壓重型機械,由剪切系統和打包系統兩部分組成,其中打包系統由門蓋、側壓和料箱組成,如圖1 所示。門蓋與料箱間通過鉸鏈連接,油缸推動門蓋使其繞鉸鏈軸線旋轉實現上壓廢料,側壓部分與料箱間采用接觸表面約束,油缸推動側壓頭實現側壓廢料。料箱是龍門剪切機打包系統中的重要支撐部件,質量占打包系統的60%,其優化質量對節材起到重要作用。在設計階段,料箱主要采用基于樣機參考和經驗設計的方法,相關尺寸參數對其性能的影響考慮并不完善。因此,需對料箱采用虛擬樣機、有限元分析和優化設計等技術進行研究,在提高料箱性能的同時減輕自重。ANSYSworkbench 提供了與ANSYS 系列求解器相交互的強大方法,并與Pro/E、NX 等CAD 軟件有著良好的雙向接口[1],是重要的CAE 分析軟件。
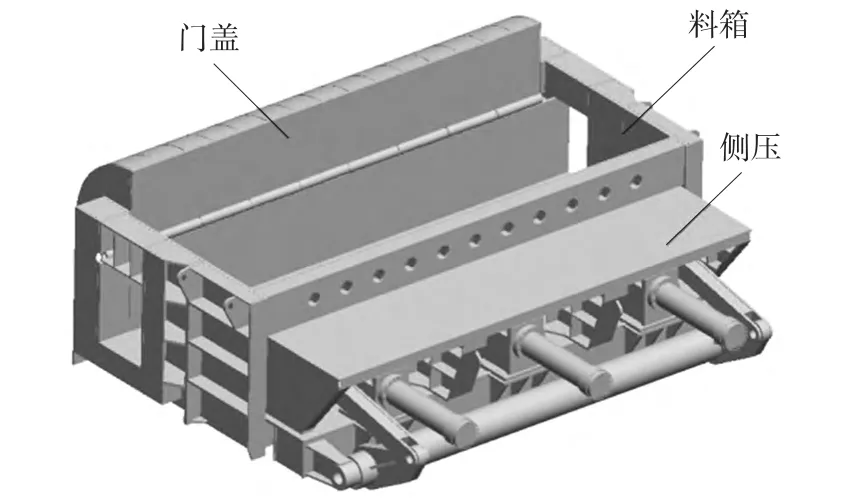
圖1 打包系統組成
本文通過在Pro/E 中建立料箱的簡化中性面模型,導入ANSYSWorkbench 中對其賦予相應的厚度,并以工作中受到的最大極限載荷工況為邊界條件,對料箱進行靜力學結構分析。根據分析結果對筋板進行合理布置并建立料箱的參數化模型,對料箱底面筋板的高度進行假設分析,對側面筋板的厚度進行靈敏度分析和多目標參數化設計,得到最優尺寸。根據優化結果重新建立料箱中性面模型并進行分析驗證。
1 靜力學分析
有限元法是在力學模型上近似的數值方法,將模型結構直接離散化并使用最小位能原理或虛位移原理等力學基本理論求解。其中結構靜力學分析包括前處理、求解和后處理三個部分[2],前處理是靜力學分析中最重要的部分,包括建立有限元模型、定義材料、劃分網格、施加載荷與約束[3]。
1.1 前處理
料箱結構較復雜,為提高分析精度和求解效率[4],需要對料箱進行適當簡化。由于料箱是由鋼板焊接而成,為得到高質量的網格采用“以面代體”的分析方法,即在Pro/E 中建立簡化的料箱中性面模型,通過接口導入ANSYSWorkbench 中賦予相應厚度。料箱的材料為Q235。
網格劃分質量決定結果的精度[5],目前Workbench 中應用程序提供了通用網格劃分格局,其中2D幾何有自動劃分、均勻四邊形劃分和三角形劃分等方法。同時ANSYS Meshing 提供多種總體及局部控制的網格劃分方法,確保了網格的質量。料箱的中性面模型采用2D 的自動劃分方法并設置單元尺寸為50mm,得到的網格單元質量為0.94。
邊界條件包括位移邊界條件和載荷邊界條件[6]。在打包過程中,包塊分別受到門蓋和側壓兩部分力的作用,在打包完成的瞬間包塊受力最大,因此取此刻的受力特點為極限邊界條件。假設包塊質量均勻且充滿整個料箱,則包塊的重量約為580kN,門蓋的重量為130kN,極限工況下,門蓋油缸的最大作用力為1862 kN,與豎直方向的角度為22°,側壓頭的重力為176 kN,極限側壓力為3624 kN,油缸各支座受到反作用力。料箱的底面筋板采用固定約束,得到的邊界條件如圖2 所示。

圖2 邊界條件
1.2 結果分析
得到的靜力學分析結果如圖3 至圖5 所示,由圖可知最大位移為0.95mm,產生在料箱側部的上端,最大應力為279.43MPa,主要集中在側部筋板與底座的連接處,由于材料的屈服極限為235MPa,因此,料箱的局部結構處已發生塑性變形。

圖3 料箱位移分布
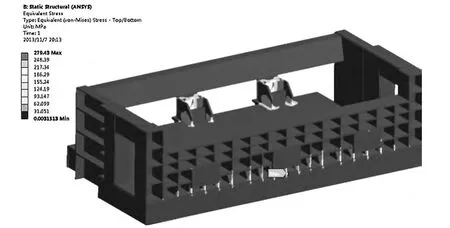
圖4 料箱應力分布(側面)
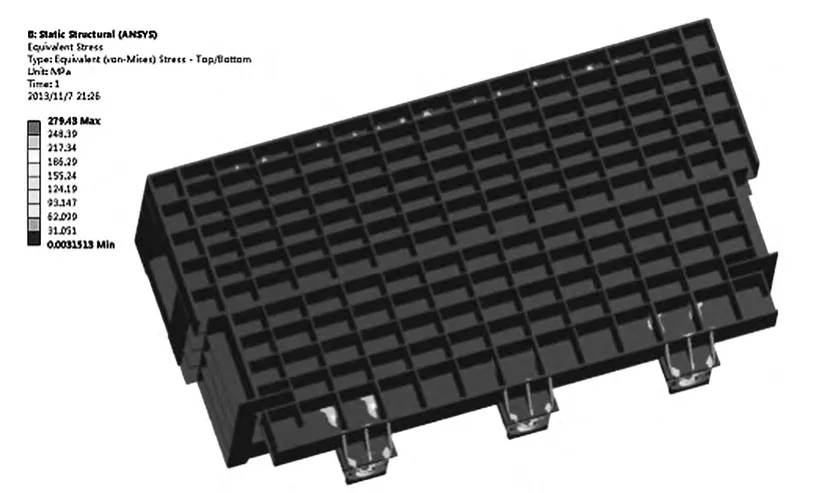
圖5 料箱應力分布(底面)
2 優化設計
2.1 筋板分布的重置
根據分析結果可知,高應力主要分布在側筋板的底部和液壓缸座處,大部分底部和側部的筋板所受應力極小。因此,可通過布置底部和側部筋板的分布進行優化設計。
料箱筋板的優化主要體在筋板數量和位置的修改,優化后的布筋方式如圖6 和圖7 所示。對此優化后的結構重新進行靜力學分析可知,料箱的最大位移為2.02mm,最大應力為318.44 MPa,相比原方案其力學性能較差,但重量減少近15t,約24.6%的自重。
為降低最大位移和最大應力,提高料箱的力學性能,將對筋板的相關參數進行優化設計。
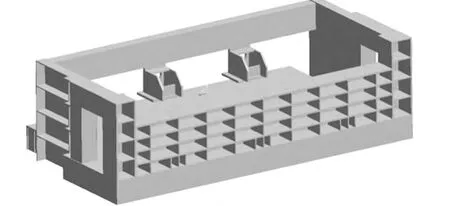
圖6 料箱筋板分布優化(側面)

圖7 料箱筋板分布優化(底面)
2.2 底板加強筋高度優化
在PRO/E 中建立料箱的參數化模型,定義底板加強筋的高度參數,在workbench 下的參數管理器中進行參數假設分析,結果如圖8 和圖9 所示,筋板的高度與最大位移成正比,與最大應力間的關系成非線性。從節材角度分析,選擇底板加強筋的高度為300mm。由于料箱的力學性能提高不明顯,將對側面筋板的厚度進行優化,以降低最大位移和最大應力。
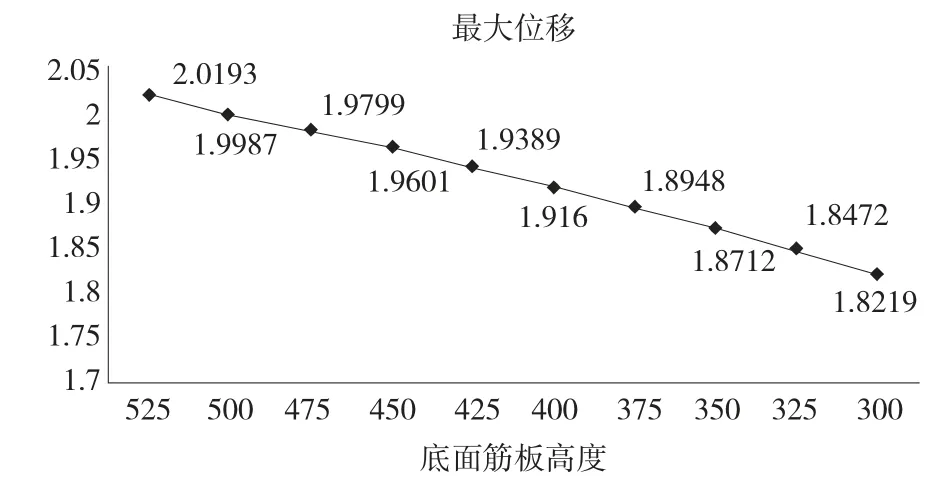
圖8 最大位移與筋板高度關系
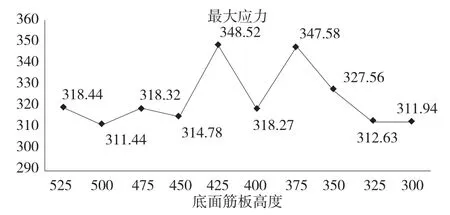
圖9 最大應力與筋板高度關系
2.3 側板加強筋厚度的優化
尺寸優化是建立在數學規劃論的基礎上,在滿足給定條件下達到最佳經濟技術指標[7-8],其過程包括建立參數化模型、結構分析、定義變量和目標函數、分析優化結果。
為便于分析,需用同一參數變量控制相同結構的厚度。在mechanical 模塊中,厚度是獨立設置,因此,建立簡化料箱的參數化實體模型,并將參數傳遞到Workbench 中進行尺寸分析。最后將得到優化尺寸反饋到中性面模型中重新進行分析對比。
側筋板的厚度參數如下圖10 所示,參數ds_1 為橫排加強筋的厚度,原值為40mm;參數ds_2 為豎排加強筋的厚度,原值為30mm;參數ds_3 為新增小加強筋的厚度,值為30mm。定義三個尺寸參數變化范圍設為25~40mm,對此模型進行靜力學分析并插入Response surface 分析,得到尺寸靈敏度分析結果如圖11。
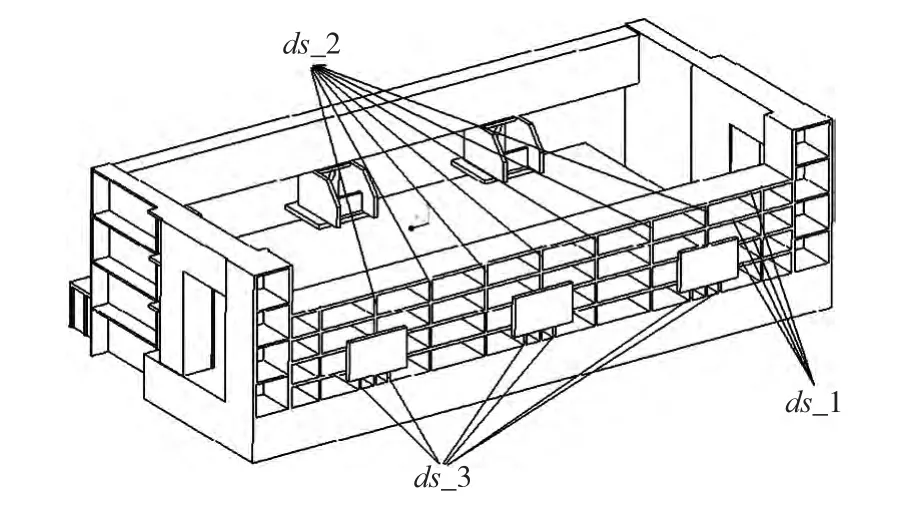
圖10 側筋板參數化
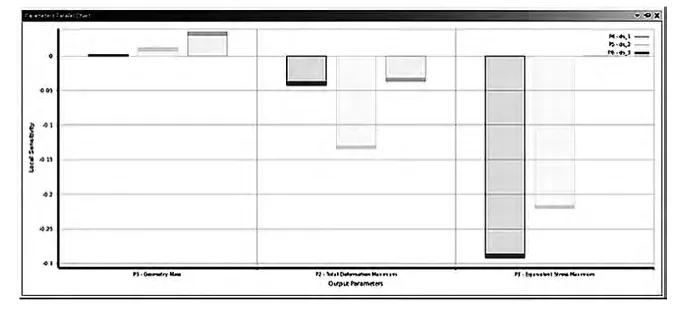
圖11 側筋板的靈敏度分析
由圖可知,尺寸1 對質量的影響最大但對最大位移和最大應力的影響最小,因此,尺寸1 取值范圍為25~30mm。觀察尺寸1 和尺寸2 對最大位移的響應面如圖12 所示,從圖中可以看出尺寸2 對最大位移起著主要作用,當尺寸1 取值在25~30mm 間時,為保證有最小的位移,尺寸2 取值范圍為35~40mm。觀察尺寸1 和尺寸3對最大應力的響應面如圖13 所示,從圖中可以看出尺寸3 對最大位移起著主要作用,當尺寸1 取值在25~30mm 間時,為保證有最小的應力,尺寸3 取值在35~40mm 間最理想。因此,ds_1 最佳取值范圍為25~30mm,ds_2 為35~40mm,ds_3 為35~40mm。

圖12 最大位移響應面
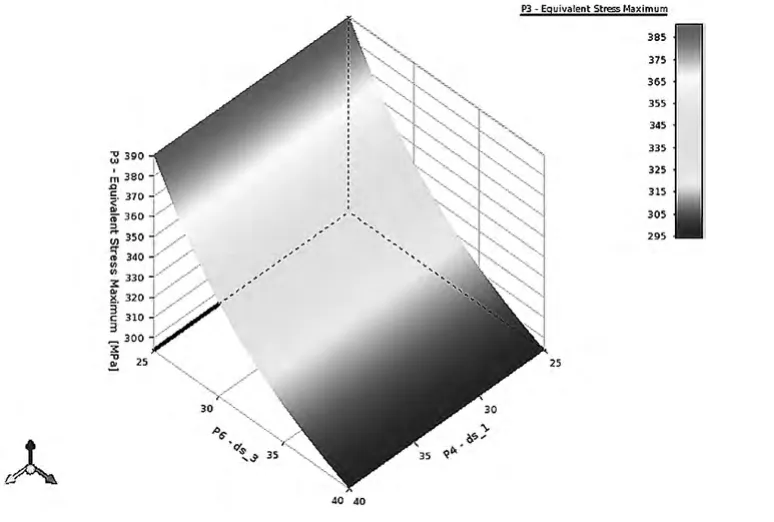
圖13 最大應力響應面
為進一步確定最佳的尺寸配合,采用多目標尺寸優化[9-10],將質量、最大位移和最大應力設為優化目標,結果如圖14 所示。為便于加工制造,優化尺寸分別采用ds_1 =26mm,ds_2 =37mm 和ds_3 =40mm。
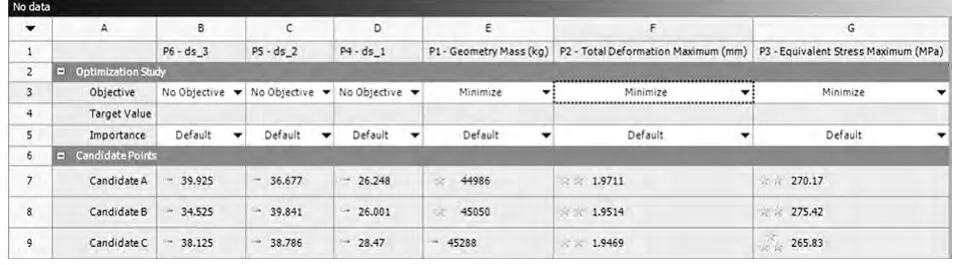
圖14 多目標參數優化結果
3 優化結果驗證
根據優化結果建立料箱中性面模型并進行靜力學分析,得到的分析結果如圖15 和圖16 所示,料箱最大位移為0.9904mm,最大應力為214.09MPa。優化前后料箱的目標參數如表1 所示,從表中可以看出優化后結構的最大位移比原方案增加0.03953mm,但最大應力減少了65. 34MPa 且節約近19. 8t 的材料,約為32.4%的自重。
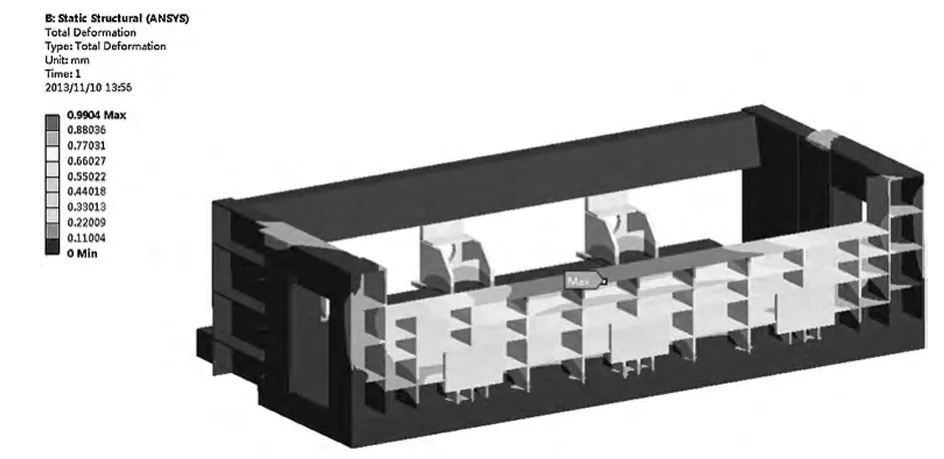
圖15 優化后料箱位移分布
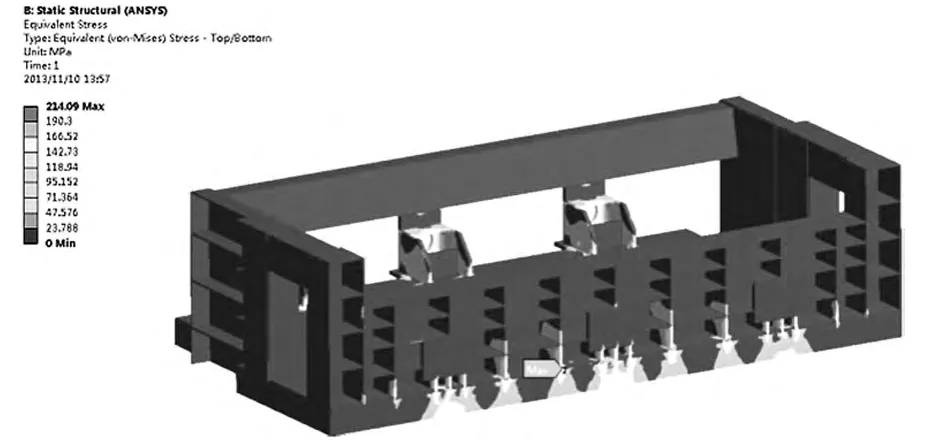
圖16 優化后料箱應力分布
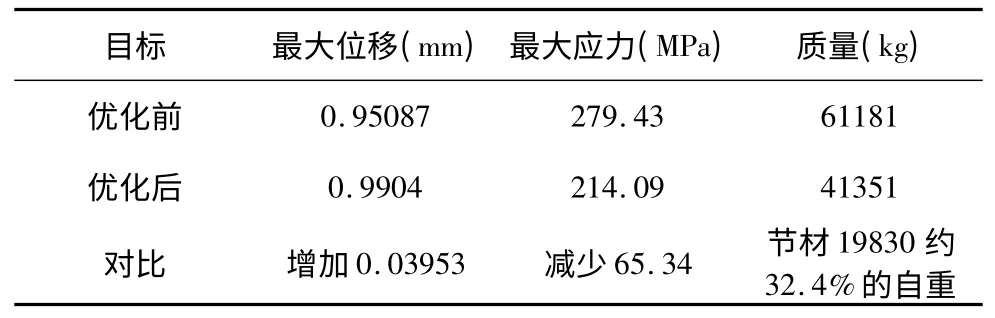
表1 優化前后對比
4 結論
建立料箱的簡化中性面模型,并在極限工況下進行靜力學分析。由于在筋板上的應力分布較為集中,因此對料箱筋板進行合理分布,并通過建立參數化模型分別對底部筋板的高度采用假設分析,對料箱側面筋板的厚度進行靈敏度分析和多目標參數化設計,最終得到合理的優化尺寸。根據優化尺寸建立料箱的中性面模型并進行分析驗證,結果表明料箱可節省19.8t的材料,實現節材32.4%。
[1]汪宇,王東方.基于ANSYSWorkbench 的立式加工中心床身有限元分析和優化設計[J]. 制造業自動化,2009,31(9):129 -131.
[2]楊永亮.基于有限元的車床床身結構優化[D]. 大連:大連理工大學,2006.
[3]葉阜,張寶國,張起偉,等.基于ANSYSWorkbench 的斗輪堆取料機關鍵零部件的有限元分析優化[J]. 起重運輸機械,2008(12):83 -86.
[4]張向宇,熊計,郝鋅,等. 基于ANSYS 的加工中心滑座拓撲優化設計[J].制造技術與機床,2008(6):68 -70.
[5]周孜亮,王貴飛,叢明. 基于ANSYSWorkbench 的主軸箱有限元分析及優化設計[J].組合機床與自動加工技術,2012(3):17 -20.
[6]MingCong,QiangZhao,TaoHan.Influence of different boundary constraint in static and dynamic analysis[C].2010 International Conference on Mechanic Automation and Control Engineering. June26,2010 -June28,2010.Wu han,China:IEEE Computer Society.
[7]龔曙光,邱愛紅,謝桂蘭.基于有限元分析的零部件優化設計研究與應用[J].機械,2002(10):23 -28.
[8]郭壘,張輝,葉佩青,等.基于靈敏度分析的機床輕量化設計[J].清華大學學報,2011,51(6):846 - 850.
[9]胡仕成,田明華,黃紅波. 基于Workbench 的正面吊臂架多目標優化設計[J]. 徐州工程學院學報,2013,28(2):57 -61.
[10]王曉軍,肖冠云. 機械優化設計中目標函數的常用優化目標及應用研究[J].重型機械技.2005(1):28 -30.

