一種改進的三維形狀非剛性對準方法

左向梅，韓鵬程

（西北工業大學航空學院，陜西 西安710072）

0 引言

計算機視覺在自動化生產的裝配線上得到了很好的應用，能夠用于識別零部件，在產品檢驗方面有著成功的應用。真實準確的數字化重建現實生活中的物體，是計算機視覺研究領域的一個重要問題，而物體的對準是在計算機中實現物體重建的一個重要步驟。三維形狀對準的目的就是找到2個或者多個三維形狀的頂點之間準確的對應關系，通過減小對應頂點之間的距離使物體發生形變。然而，在現實生活中存在著大量的非剛性物體，當這些非剛性物體發生非剛性形變時，許多基于三維形狀剛性形變對準的重建假設和方法已經不再適用，非剛性形變物體的對準已經成為一個急需解決的技術問題。

剛性對準只需要根據一些對應關系就可以定義一個候選剛性變換來進行假設測試，非剛性情況下還需要變形和對準信息，因為它沒有足夠的先驗假設，經常需要很多更加可靠的對應來定義變換。此外，非剛性對準還需要考慮變形，因此，相比于剛性對準，非剛性對準更加困難。

為了克服現有對準方法性能差，易產生畸變，對三維形狀完整性要求高，適用范圍小，對準精度低的問題［1－3］，提出了基于相關點漂移和動態形變圖相結合的三維形狀非剛性形變的自動對準方法。

1 相關點漂移

相關點漂移（CPD）［2］是一種基于概率的點集非剛性配準算法，該算法被視為基于速度場運動一致性約束的最大似然估計問題。在CPD算法中，一個點集作為高斯混合模型的內核，另一個點集作為高斯混合模型的數據，采用確定性退火的EM算法［4－5］對最大似然估計進行優化，從而找到2個點集的對應關系與非剛性變換，即內核點集向數據點集配準。這種方法可以估計復雜的非線性和非剛性變換，而且在含有噪聲和溢出點的情況下有較強的魯棒性。

方法中，將源模型的頂點看作數據集Y＝（y1，…，yM）T，將目標模型的頂點看作產生數據集的高斯混合模型的中心（內核點集）X＝（x1，…，xN）T，通過EM［4－5］算法計算數據集中的點，對應混合高斯模型中心的后驗概率，從而確立源三維形狀頂點和目標三維形狀之間的對應關系，利用所得的對應關系，將2個三維形狀進行非剛性粗對準。

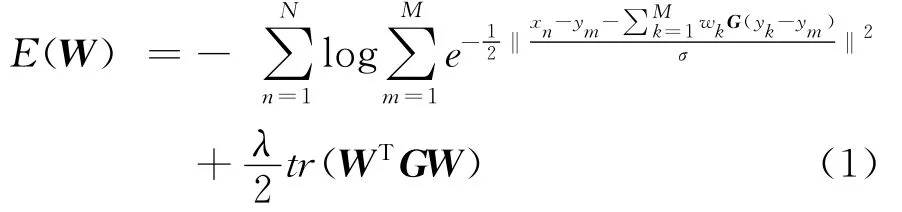
GM×M為對稱方陣；W＝WM×D＝（w1，…，wM）T為高斯內核矩陣；D為點云集的維數，取D＝3；N，M分別為源三維形狀頂點和目標三維形狀頂點的個數；tr為向量的跡；λ為常數。

具體來說，相關點漂移算法的步驟為：

a．初始化系數矩陣W＝0，協方差σ2，參數ω（0≤ω≤1），β＞0，λ＞0。

b．構建核矩陣GM×M，矩陣元素gij＝G（yi，yj）

c．EM算法優化。通過高斯混合模型聚類的EM 算法推導，能得到式（1）的上界［6］，即

G（m，·）表示G的第m 行。最小化Q就相當于最小化式（1）的能量函數。

在E步中，計算后驗概率矩陣P，其元素表達式為：

后驗概率pmn表示了頂點xn和ym之間的對應概率。

在M步中，優化求解W，對式（2）關于W 求導，得到方程：

1為元素全為1的列向量；d為對角陣。兩邊同乘以σ2G－1，得到方程的線性系統，即

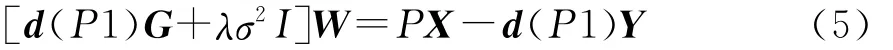
從式（5）中解出W。

d．重復步驟c，直至收斂。

當算法收斂后，三維形狀點之間的對應關系由后驗概率矩陣給出，相應的對準后的三維形狀T＝T（Y，W）＝Y＋GW。

2 形變圖驅動模型對準

2．1 構建動態形變圖

圖模型本身的形變方式是通過對每一個結點應用對應的仿射變換，因此，對于結點自身，有槇gj＝gj＋tj。

對于原始模型上的任意頂點vi，其形變后的位置槇vi可以通過圖模型每個結點的形變加權求和得到，也就是將形變圖結點的變換外推到模型上每個頂點，即

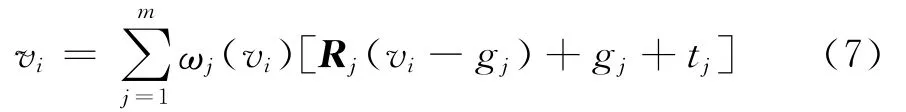
ωj（vi）是與vi和gj之間距離d（gj，vi）相關的權值，ωj（vi）＝max｛0，［1－d2（gj，vi）／r2i］3｝。

該點的法向量也被相似變形：

這里使用邊融合技術，在指定向下采樣的三維模型面個數情況下，實現均勻采樣，從而構建出原始三維模型的動態形變圖，用來驅動三維形狀的對準。

使用動態形變圖來驅動原始三維形狀的非剛性對準可以減少變量個數，降低運算量，縮短運算時間，提高三維形狀非剛性對準的效率。手模型與其形變如圖1所示。

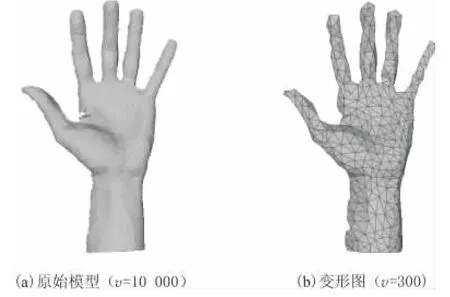
圖1 手模型及其形變

2．2 動態形變圖驅動模型對準

通過求解形變圖的變形來驅動原始模型的變形。在非剛性對準中，需要對圖模型的結點求解未知的旋轉變換和平移變換（Ri，ti）。保留特征的變形場可以通過使用下面的能量最大化局部剛性得到：

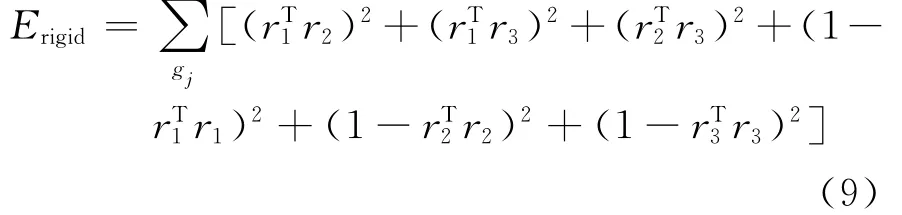
r1，r2，r3為Ri的列向量，上式從正交和單位長度方面測量了列向量的偏差。還需要額外的正則項確保變形的光滑性：

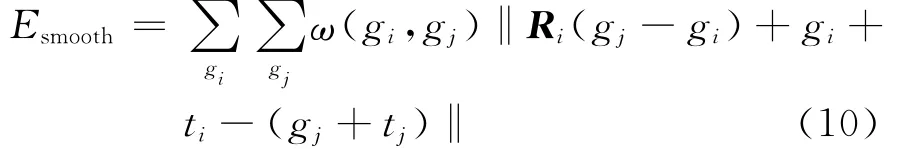
Esmooth項描述了每個節點與其周圍節點形變具有相容性。最小化Esmooth保證了整個三維形狀在對準過程中表面的光滑性。

引用非剛性ICP算法［6］思想，迭代計算最近點對應關系，隨后進行修剪和變形步驟。為了避免非線性優化中的局部最小化，采用逐漸放松形變模型的正則能量系數的策略［7］。

尤其是免門票的方式可以吸引更多的消費者，這也代表著當前旅游發展模式的方向，可以擴大旅游資源的利用效率，企業員工、游客、社區居民可在園區內共享優美環境、共享改革開放的成果，這也是全域旅游的目標導向之一。

因為輸入數據在時間上具有一致性，所以重復地在源模型和目標模型之間使用最近點對應來決定最優的形變。為了獲得較準匹配，對應能量由點到點和點到面的度量組成，以避免在特征較少區域出現的不正確對應：

αpoint＝0．1，αplane＝1，槇vi為原始源模型上的點經過動態形變圖映射后對應的新的坐標位置；ci為原始目標模型上與槇vi對應的點；C為所有對應點對組成的集合；Efit描述了需要對準的三維模型點與點及點與平面之間的距離。

為了求解（Ri，ti），建立目標能量函數：

初始化時取高的權值αsmooth＝50，αrigid＝100，此后通過最小化式（12），交替地進行對應點對的計算和形變。

2．3 高斯－牛頓法優化目標函數

使用高斯牛頓法最小化目標函數（7），高斯牛頓法源于無約束優化的牛頓算法。非線性最小二乘優化問題中的目標函數形式比較特殊，可以得到其雅克比矩陣的具體形式，將其代入牛頓法的迭代公式中，就可得到高斯牛頓法。

算法的具體步驟如下：

a．給定初始點x（0），精度σ＞0，置k＝0。

b．計算f（xk），S（xk）。

f．置x（k＋1）＝x（k）＋x。

g．檢驗終止原則，否則令k＝k＋1，轉步驟b。

通過上述優化過程，保證了Ri的單位正交性，使三維模型不會發生扭曲畸變；使每個結點與其周圍結點的形變具有相容性，確保這個三維模型在對準工程中表面光滑；不斷縮小需對準的點與點及點與平面之間的距離，使三維模型朝著目標方向發生形變，最終完成三維形狀的非剛性對準。

3 實驗結果

用多組實驗數據驗證了方法的有效性，所有實驗均在Inter Core（TM）2 Duo E7500 CPU，2 GB內存的Windows XP操作系統上，基于Matlab平臺進行。其中，源模型和目標模型均為由Kinect對人體運動進行拍攝拼接得到的三維模型［8］。

在實驗中，對于不同模型，CPD的參數選擇對于實驗結果影響較大。如圖2所示，圖2a為源模型與目標模型；在圖2b中，β＝2．0，λ＝1．0；在圖2c中，β＝3．0，λ＝1．0。由此可以看出，CPD的β參數影響對準后源模型的光滑性，β越大，光滑性越好。模型描述及實驗結果如表1所示。

由表1可以看出，對于中等數據和大數據模型，算法都能在相對較短的時間內取得較好的配準精度。形變圖結點數目對實驗速度和精度有一定影響，點數越多，時間越長，匹配精度越高。

圖2 CPD參數影響

表1 模型描述及實驗結果

4 結束語

提出了三維形狀的非剛性形變自動對準方法，通過使用相關點漂移算法結合動態形變圖技術，在不依賴任何幾何特征的情況下，可以自動對準發生非剛性形變的完整或不完整的三維模型。實驗結果表明，即使對數據缺失比較嚴重或者形變較大的模型，此方法也能取得較好的效果，具有魯棒性強、對準精度高、自動化程度高和應用范圍廣等優點。

［1］ Hou T，Qin H．Robust dense registration of partial nonrigid shapes［J］．IEEE Transactions on Visualization and Computer Graphics，2012，18（8）：1268－1280．

［2］ Myronenko A，Song X．Point set registration：coherent point drift［J］．IEEE Transactions on Pattern Analysis and Machine Intelligence，2010，32（12）：2262－2275．

［3］ Fabry T，Smeets D，Vandermeulen D，et al．3D non－rigid point cloud based surface registration based on mean shift［C］．Proceedings 18th International Conference on Computer Graphics，Visualization and Computer Vision，2010．121－128．

［4］ 張祥德，唐青松．確定性退火技術在點配準中的應用［J］．東北大學學報（自然科學版），2003，24（11）：1119－1122．

［5］ 王 源，陳亞軍．基于高斯混合模型的EM學習算法［J］．山西師范大學學報（自然科學版），2005，19（1）：46－49．

［6］ Allen B，Curless B，Popovi Z．The space of human body shapes：reconstruction and parameterization from range scans［J］．ACM Transactions on Graphics，2003，22（3）：587－594．

［7］ Sumner R W，Schmid J，Pauly M．Embedded deformation for shape manipulation［J］．ACM Transactions on Graphics，2007，26（3）：80－86．

［8］ Vlasic D，Peers P，Baran I，et al．Dynamic shape capture using multi－view photometric stereo［J］．ACM Transactions on Graphics，2009，28（5）：174－185．