直線超聲電機精密運動平臺系統模型辨識

曹會平，葉 明，姚志遠，李曉牛

（1．南京航空航天大學電子信息工程學院，江蘇 南京210016；2．南京航空航天大學機械結構力學及控制國家重點實驗室，江蘇 南京210016）

0 引言

直線超聲電機是利用壓電陶瓷的逆壓電效應、結構的超聲振動使其運動，并通過定／動子的摩擦耦合，將結構的微幅振動轉換成動子的宏觀直線運動［1］。受壓電能量轉換和摩擦傳遞等的非線性和分散性影響［2］，直線超聲電機在運行的過程中表現出較強的時變、非線性和強耦合，故實現其精確定位控制也就變得復雜了。為直線超聲電機運動平臺建立合理的數學模型，估算某輸入條件下電機、平臺的輸出特性，成為解決超聲電機控制的重要手段之一。

近些年，國內外學者在超聲電機建模方面做了大量工作［3－8］。大多研究工作集中在超聲電機自身的辨識系統上，對超聲電機平臺的整體辨識研究還比較少；研究對象多為旋轉型電機，對直線電機模型辨識的研究也較少。在對電機平臺進行研究時，平臺除電機外的其他外圍設備也會對系統模型產生影響，僅用電機模型代替電機平臺進行試驗是不準確的。為提高系統模型準確性，對平臺進行更加精確的控制，將電機平臺作為一個整體進行研究是非常有必要的。

因此，搭建了一個直線超聲電機運動平臺。建立了直線超聲電機運動平臺的電壓－位移模型。通過比較實際輸出與模型輸出曲線差異的試驗研究，驗證了所建系統模型的正確性。為了將平臺模型用于定位控制，針對平臺模型參數的變化，將各個參數看作是以輸入電壓為自變量的函數，采用最小二乘法分別對其進行多項式擬合，最后通過實驗仿真，得到擬合前后模型輸出曲線，從而證明了擬合數據的正確性。

1 直線超聲電機運動采集平臺

直線超聲電機運動采集平臺由數據采集設備（包括凌華科技PXI－3910嵌入式控制器和NI PXI－6229數據采集卡）、直線超聲電機運動平臺和信號調理電路構成。其結構如圖1所示。

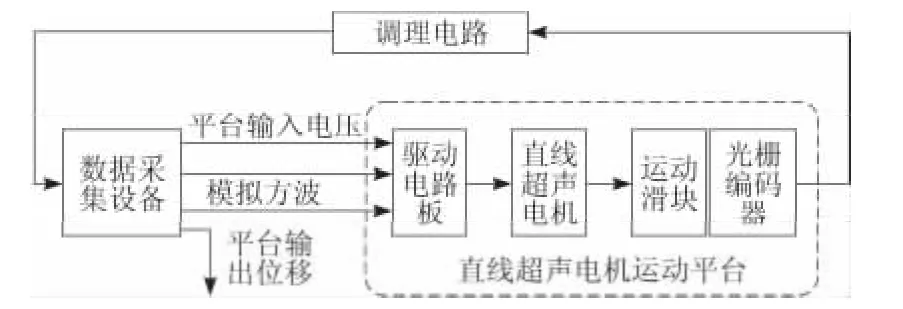
圖1 超聲電機運動采集平臺結構

其中，PXI－3910控制器采用Intel Celeron M 處理器，為位移采集提供了穩固的操作環境，通過人機交互界面實現數據采集卡端口定義、參數設置、數據收發及處理等功能［9］。PXI－6229數據采集卡具有16位量化精度，32路單端A／D模擬輸入通道，4路模擬輸出通道，2個32位通用計數器，滿足平臺輸入、輸出信號端口數目和精度等要求。

直線超聲電機運動平臺包括直線超聲電機驅動板、直線超聲電機和裝有光柵編碼器的運動滑塊。驅動電路板產生2路頻率可調的正弦信號直接作用于電機，驅動電機運動；后兩者構成平臺的位移信號生成裝置，其實物如圖2所示。系統所用的電機是具有連續變截面振子的V形直線超聲電機，通過固定盒固定在運動滑塊前端。運動滑桿與電機定子無縫接觸，其一端連接運動滑塊，運動滑塊固定在導軌上，只能沿導軌做直線往返運動。在驅動信號作用下，電機定子推動滑桿運動，滑塊相應運動，光柵編碼器讀頭發出位移信號。

圖2 位移信號生成裝置實物

實驗中，PXI－6229數據采集卡2路AO口輸出方波信號模擬電機驅動板開關，通過改變輸出方波的頻率以及占空比，控制電機運行時間；1路AO口輸出模擬電壓，作為平臺輸入電壓信號作用于電機驅動板；1個計數器通道接收調理后的光柵尺信號。當上位機Lab VIEW程序控制數據采集卡輸出2路方波開啟電機運動時，另一路電壓階躍信號同時輸入驅動板，經壓控振蕩、分頻、功率放大和電感匹配后，輸出2路相位差為的正弦信號驅動電機運動，電機推動滑塊運動，使其上的光柵尺產生A＋／A－，B＋／B－差分信號，該差分信號再經其后的調理電路轉換成A，B 2路單端脈沖信號，數據采集卡采集A，B信號，經上位機處理得到平臺運動位移。正弦信號的頻率與電壓階躍信號在某一范圍內呈線性關系，故改變數據采集卡輸出階躍電壓實際上也就是改變電機驅動信號的頻率，從而影響電機運動位移。為了實現正弦信號頻率微調，該模擬輸出電壓需要精確到小數點后3位，PXI－6229的16位量化精度完全滿足系統需要。

2 實驗設計與數據分析

在實驗中，運動平臺數學模型以輸入超聲電機驅動板的某一幅值階躍電壓信號為輸入信號，在該電壓下運動平臺運行某一固定時間的輸出位移信號為輸出信號。由于超聲電機響應時間僅為ms級，且實驗運動平臺總行程為6 cm左右，故實驗中選擇電機運行時間為200 ms，此時電機運行平穩且運動位移未超平臺行程。由于電機諧振頻率約為31．9 k Hz，對應的輸入電壓值為1．508 V，所以輸入電壓在［1．10 V，1．65 V］范圍內時，電機可以正常運行。為了準確研究平臺的動態特性，數據采集過程中輸入電壓信號必須在電機正常運行范圍內且覆蓋其諧振頻率。在電機諧振頻率31．9 k Hz左右改變輸入電壓幅值，采集10組數據點。實驗表明，超聲電機關斷后，負載在10 ms內就會停止運動，位移值穩定不變。因此，考慮采集信號的完整性，電機關斷后，使數據采集卡繼續連續采集10 ms位移信號，得到平臺整個運動過程中的位移數據點。同時，為了減小誤差，每個輸入電壓條件下測量多次位移輸出，將位移平均值作為平臺位移信號輸出。

實驗輸入的階躍電壓與平臺運行位移數據如表1所示。一方面，由于超聲電機性能受輸入電壓影響較大，所以改變輸入電壓，平臺運行位移變化也較大；另一方面，超聲電機的非線性決定了在輸入電壓基本均勻變化的條件下，輸出位移變化不穩定。

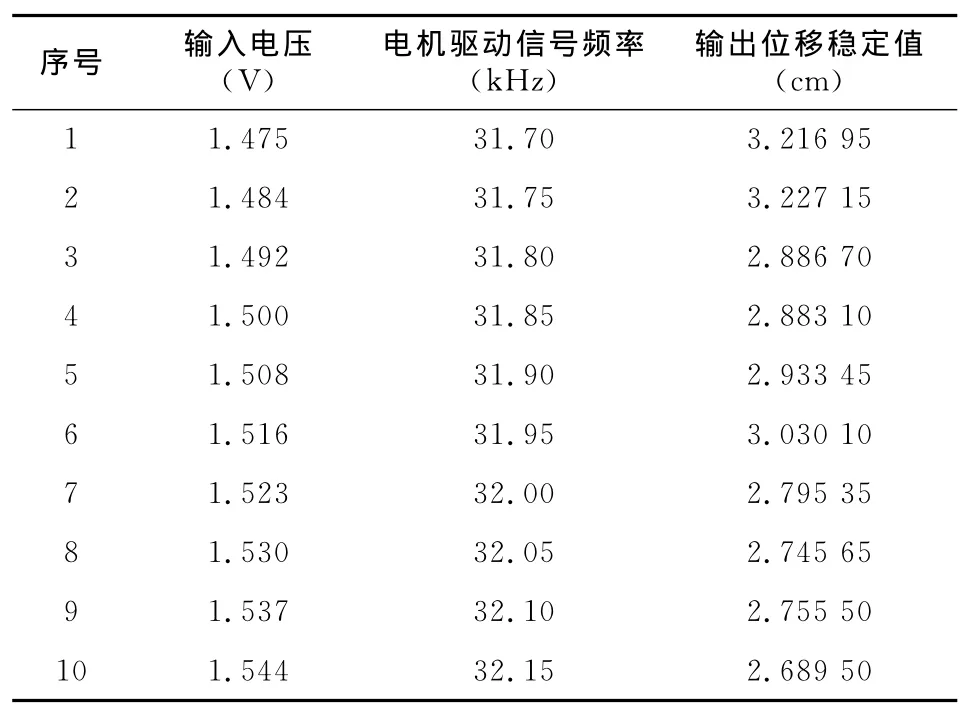
表1 輸入階躍電壓與輸出位移數據

3 模型辨識

不同輸入電壓條件下，電機平臺階躍響應曲線為欠阻尼系統，且傳遞函數的參數會隨輸入電壓變化而變化。為研究方便，簡化模型將其看做二階欠阻尼系統，可設直線超聲電機平臺傳遞函數為：

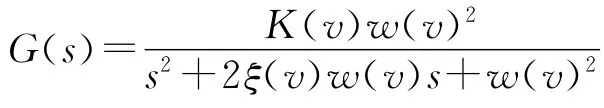
K（v）為放大系數；ξ（v）為二階系統的阻尼比；w（v）為二階系統的無阻尼自然振蕩頻率；v為平臺輸入電壓值。

利用Matlab系統辨識工具箱，分別對表1中10組數據進行模型辨識，建立以電機運動平臺電壓階躍信號為輸入信號、平臺位移信號為輸出信號的0零點、2極點的傳遞函數模型，得到平臺模型表達式。模型參數及得到的模型階躍響應與實際響應匹配度如表2所示。從匹配度來看，系統辨識得到的模型與實際模型較為吻合。

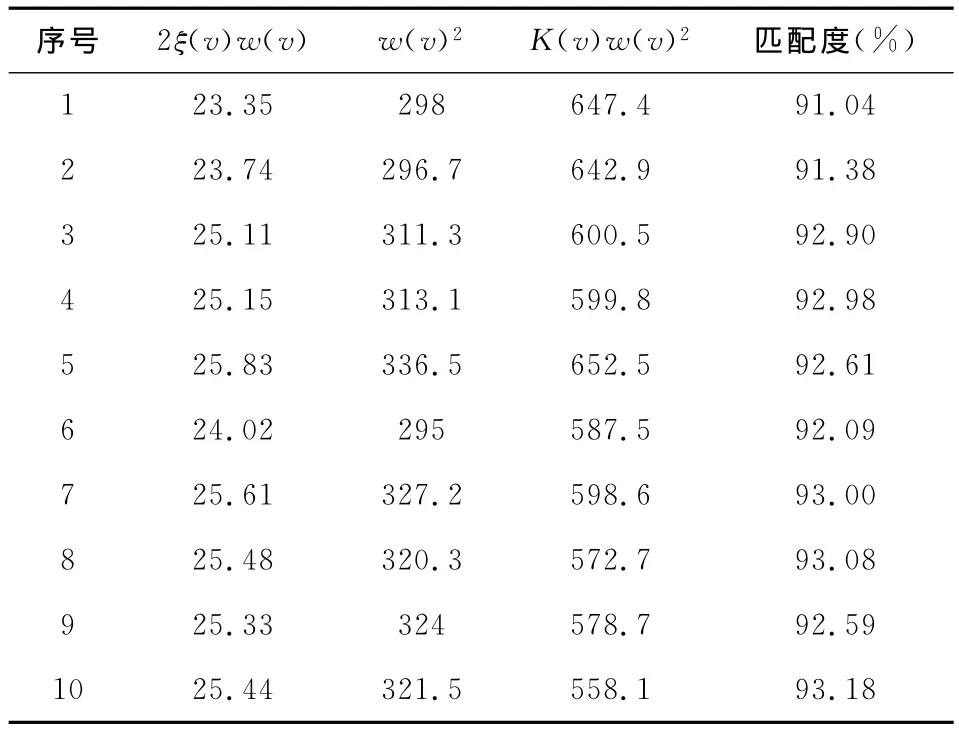
表2 系統辨識模型參數值

以第1組數據為例，將實測位移值與平臺模型辨識得到的階躍響應結果比較，如圖3所示。由圖3可以看出，系統辨識得到的位移值與實際位移值基本相同。兩者之間的誤差主要是由于將平臺看做二階系統造成的，隨著平臺階數的增加，模型將趨于逼近真實模型。實驗表明，當模型取七階系統時，匹配度接近100%，但七階系統增加了模型的復雜度，且不利于對平臺控制分析。

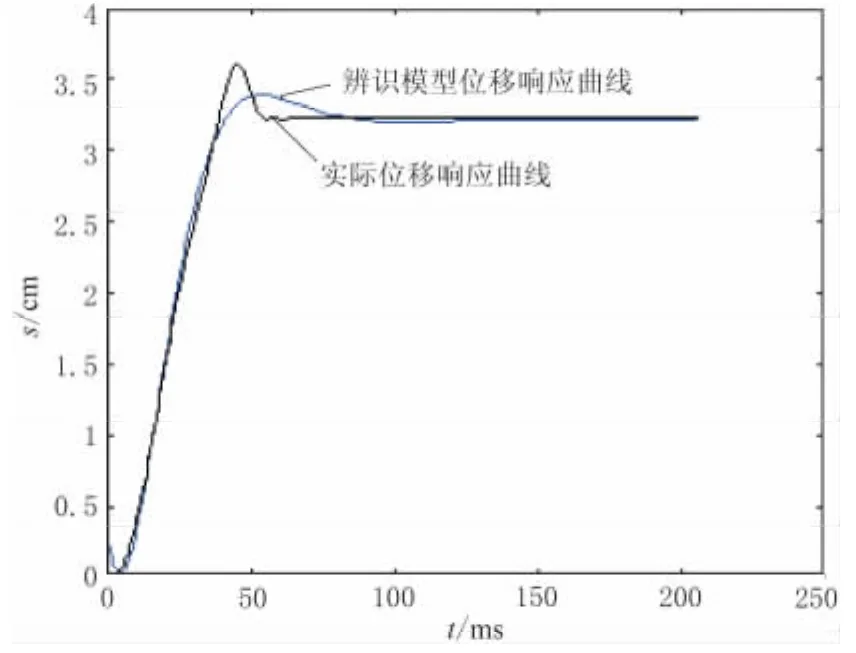
圖3 實際位移與平臺辨識位移響應曲線

4 參數擬合與擬合模型仿真

由表2也可以看出，得到的模型參數是自變量為輸入電壓的函數。以最小二乘法為準則，利用Lab VIEW進行二次多項式擬合，并根據擬合多項式，得到擬合后模型參數值如表3所示。

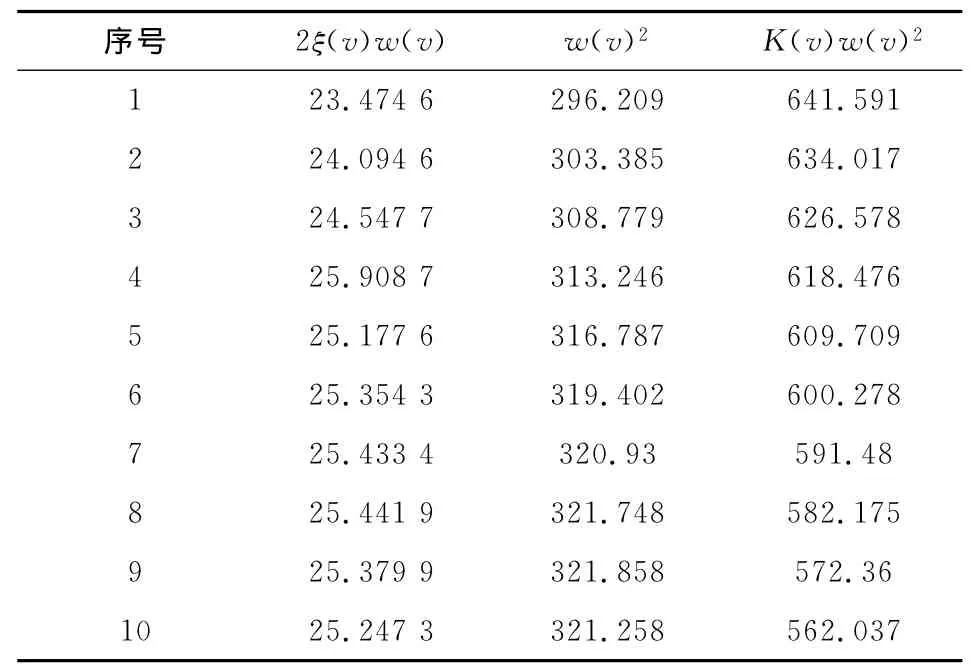
表3 多項式擬合后的參數值

利用Simulink對系統辨識模型進行仿真，得到參數擬合前后的平臺階躍響應曲線如圖4所示，其中擬合前階躍響應用虛線表示，擬合后階躍響應用實線表示。由2條曲線對比可以看出，擬合結果較理想。

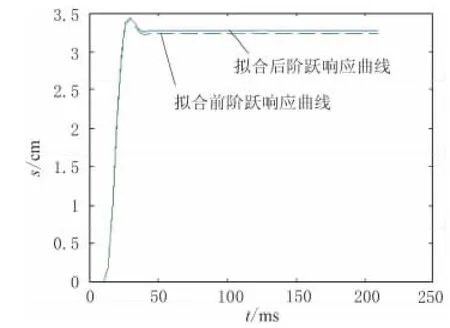
圖4 參數擬合前后的平臺階躍響應曲線

5 結束語

將直線超聲電機運動平臺看做二階欠阻尼系統，利用Matlab自帶系統辨識工具箱，對平臺進行辨識得到辨識模型。通過擬合得到以輸入電壓信號為自變量的模型參數的函數，并對參數擬合后的模型進行仿真。從仿真結果可以看出，利用Matlab系統辨識工具箱，可以靈活、方便地計算得到系統模型，且所得模型與實際模型較吻合。

［1］ 陳廉清，任敏杰，張振祥．直線型超聲波電機及其應用［J］．微電機，2005，38（4）：76－78．

［2］ 史敬灼．超聲波電機運動控制理論與技術［M］．北京：科學出版社，2011．

［3］ Frangi A，Corigliano A，Binci M，et al．Finite element modeling of a rotating piezoelectric ultrasonic motor［J］．Ultrasonics，2005，43（9）：747－755．

［4］ 劉 博，史敬灼．超聲波電機頻率－轉速控制的階躍響應建模［J］．微電機，2010，43（11）：77－80．

［5］ 史維佳．超聲電機建模及實驗研究［D］．哈爾濱：哈爾濱工業大學，2011．

［6］ 黃青華，魏守水，趙淳生．超聲電機的等效電路模型及其參數辨識［J］．微電機，2003，36（5）：14－16．

［7］ 王心堅，金 龍，堯 波，等．行波超聲波電機非參數辨識模型［J］．中國電機工程學報，2008，28（18）：83－89．

［8］ 張建桃，張鐵民，梁 莉，等．直線超聲電機非線性模型辨識［J］．華南師范大學學報（自然科學版），2012，44（3）：64－67，74．

［9］ 張鍵滔，姚志遠，宋小剛，等．基于虛擬儀器的直線超聲電機機械特性測試［J］．振動、測試與診斷，2012，32（2）：218－222．