任意帶狀矩陣的求逆問題研究

鄧勇

任意帶狀矩陣的求逆問題研究

鄧勇

喀什師范學(xué)院數(shù)學(xué)系,新疆喀什市844006

對稱Toeplitz矩陣、Toeplitz矩陣以及三對角矩陣在數(shù)學(xué)的眾多領(lǐng)域有著廣泛應(yīng)用,尤其是三對角或更一般的帶狀矩陣經(jīng)常被應(yīng)用于解偏微分方程的有限差分法和求解變系數(shù)線性遞歸方程等問題之中.所謂r-帶狀矩陣Br,n,(1≤r≤n)指的是當(dāng)-r≤i≤r,1≤j≤r時元素為{aij},而剩下的其他元素全為零的n×n階矩陣且r稱為其帶寬.在已有文獻(xiàn)中,關(guān)于r-帶狀矩陣的許多特殊情況(r=1,2,3)的求逆問題已經(jīng)得到徹底解決.為將這些結(jié)果一般化,對Mallik方法進(jìn)行了推廣,并獲得了r-帶狀矩陣Br,n的LU分解和求逆(如果存在)公式.特別地,當(dāng)r=n時,它成為計算可逆方陣逆矩陣的新途徑.

三角矩陣;Hessenberg矩陣;逆矩陣;r-帶狀矩陣

1 引言

目前，關(guān)于矩陣的求逆(如果存在)問題已有多種方法。例如：高斯——若當(dāng)法、三角分解法、Cholesky分解法以及目前非常流行的分塊求逆法等[1,2,3,4]。眾所周知，對角矩陣A=diag( a1,…,an)的逆為A-1=進(jìn)一步，若U是兩對角矩陣，設(shè)為：

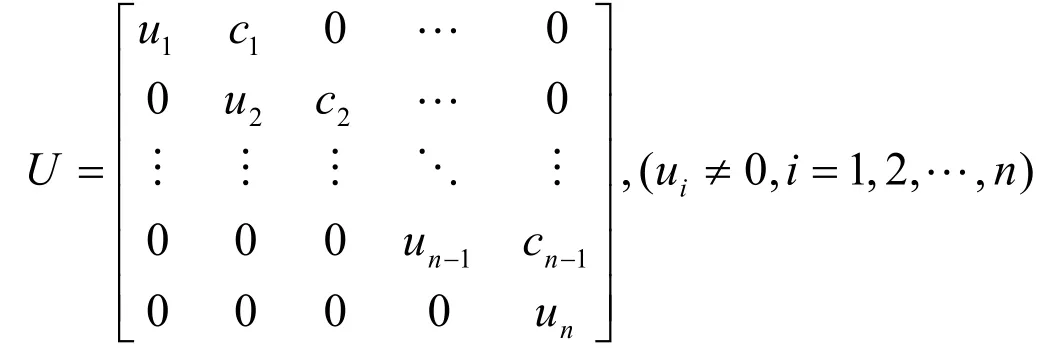
則U-1=(vij)，其中：

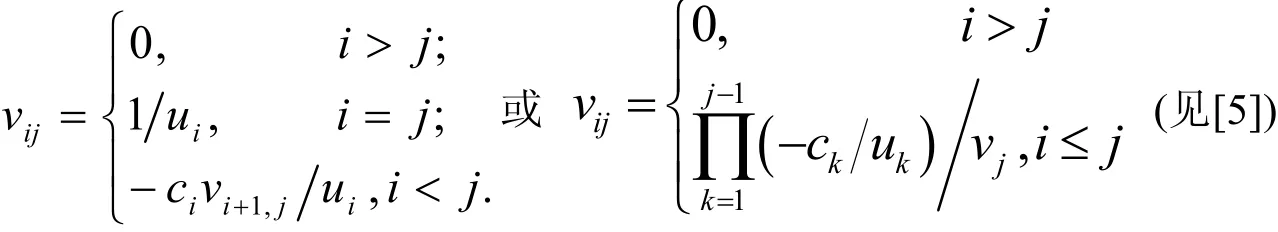
H B Li和M E Mikkawy等學(xué)者[6,7]證明了B-1=(cij)，其中：

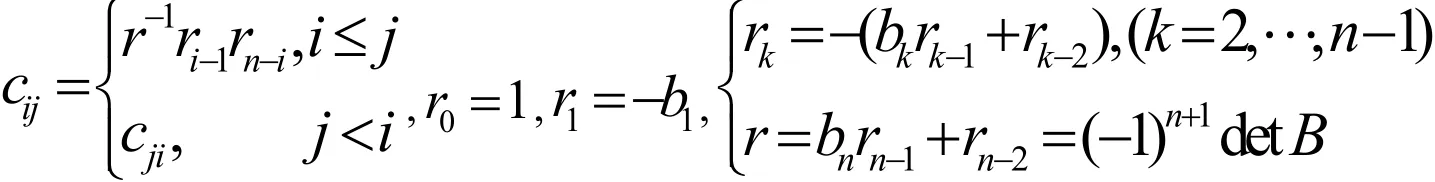
由此可見，三對角矩陣的逆矩陣是非稀疏的，因此，分塊求逆法對它不適用.基于這個原因，E Kilic利用反向連分?jǐn)?shù)得到了三對角矩陣求逆的另一種特殊方法[8]。

一般地，我們定義n階r-帶狀矩陣,rnB為：

2 r-帶狀矩陣的LU分解

為獲得r-帶狀矩陣,rnB的LU分解，我們先構(gòu)造兩個遞歸數(shù)列，對1ir≤≤和1sr≥≥，定義

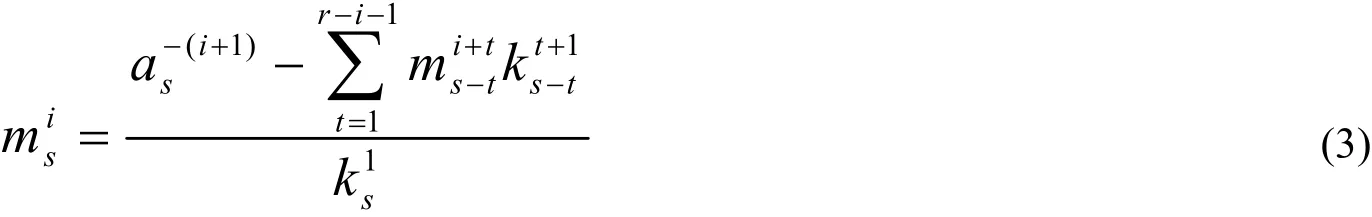
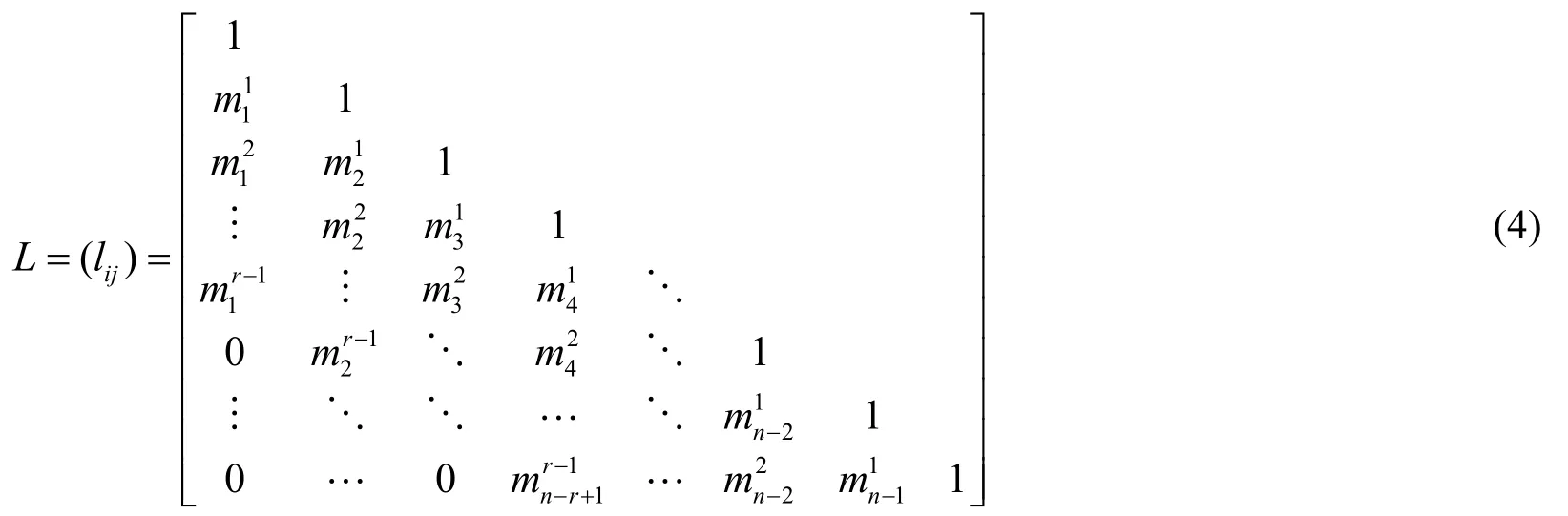
和

我就感覺這五個字非常厲害，任何矛盾和問題只要用上這五個字，立馬就能化掉百分之八十。不信你可以在生活中試驗一下，奇跡馬上就會出現(xiàn)。這可能就是導(dǎo)致成功者與失敗者兩種人生狀況的原因。

定理1當(dāng)1n＞時，r-帶狀矩陣,rnB的LU分解為,rnBLU=，其中L和U分別由(4)和(5)所定義。

證明Ⅰ.考慮i=j的情況，當(dāng)1≤i=j≤r 時，由矩陣乘法及L和U的定義，可得：

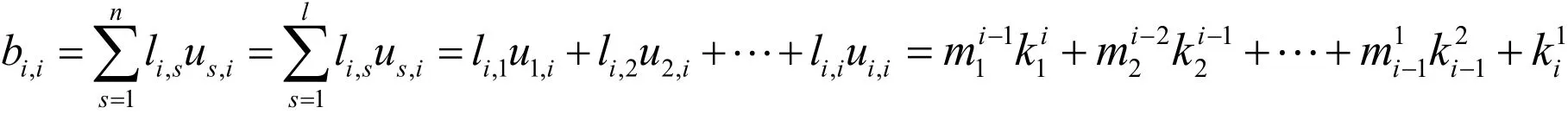
在(2)中取r=i，可得bi,i=a1i.當(dāng)i=j＞r時，由矩陣乘法及L和U的定義，可得：

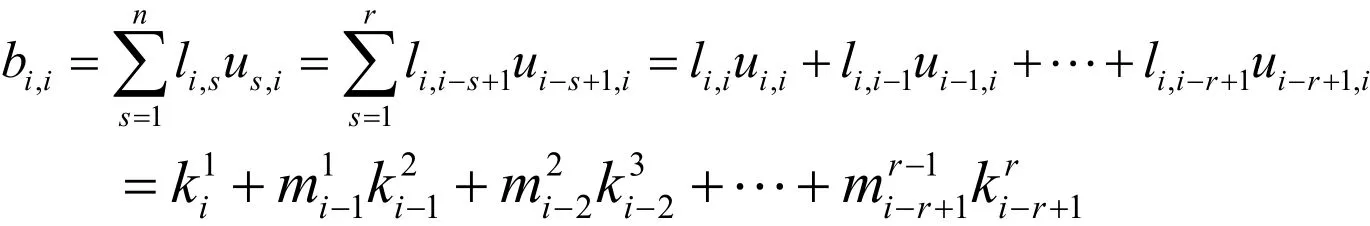
在(2)中取i=1，可得bi,i=a1n。綜上可知結(jié)論對i=j成立。

Ⅱ考慮ij≠且ji＞的情況，當(dāng)jiq=+,11qr≤≤-時，由,rnB的定義，可知：

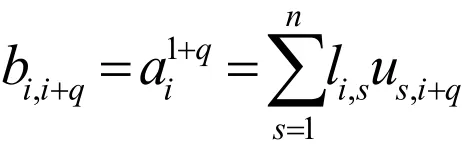
下面分兩種情況討論。首先，假設(shè)1≤i≤r-q ，因此有

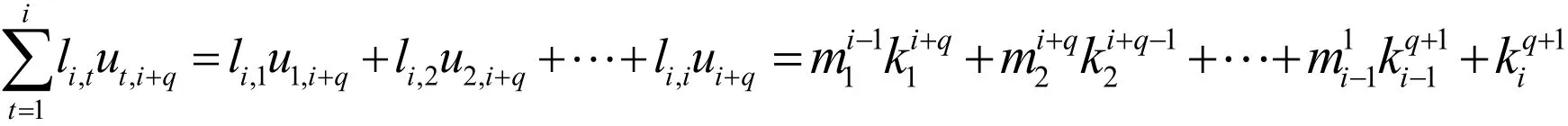
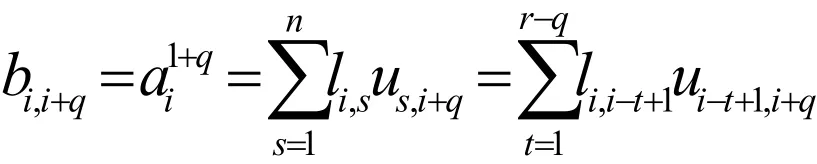
由矩陣U和L的定義，上式可寫成：

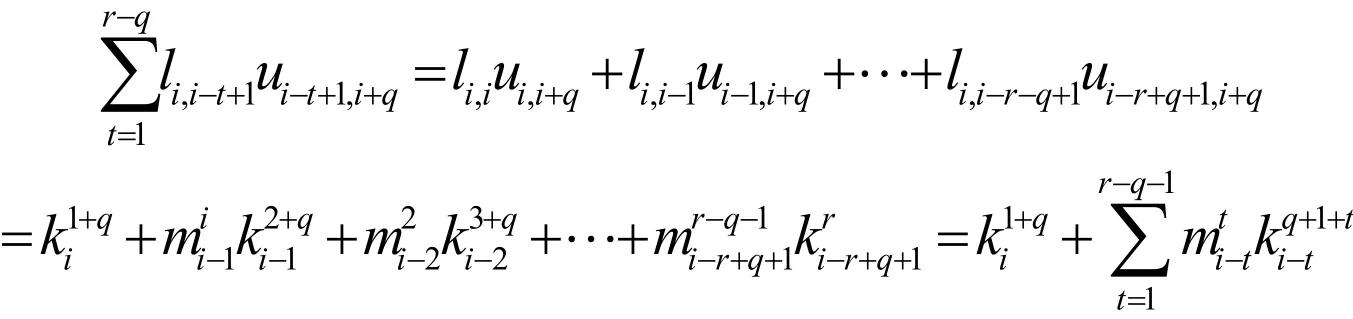
Ⅲ考慮i≠j且j＜i的情況，首先，設(shè)1≤i≤r-q ，由矩陣U和L的定義可得：

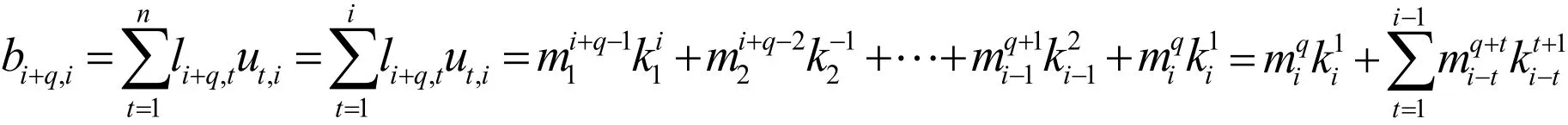
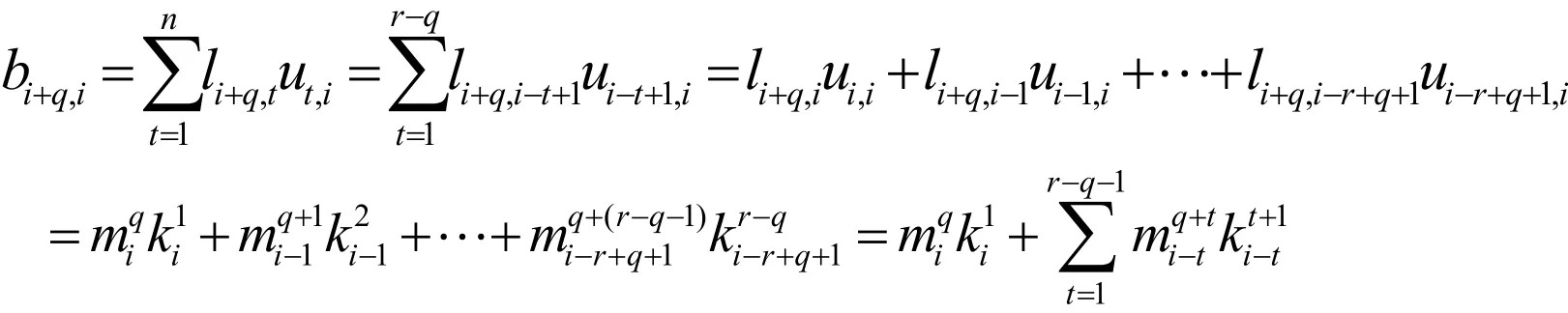
在(2)中取n=i和i=q，可得b=a-(q+1)，證畢。

i+q, ii

注：若在矩陣,rnB中取rn=,則定理1的結(jié)果對任意方陣的LU分解都有效。

由Br,n的LU分解立即可得det(Br,n)的一個計算公式，即

3 三角形矩陣的逆

為獲得一般三角形矩陣的求逆公式，我們先構(gòu)造三角形矩陣的Hessenberg子矩陣，并計算其行列式,進(jìn)而確定三角形矩陣的逆矩陣元素。這里只討論上三角形矩陣的情形，對下三角形矩陣類似可得。設(shè)H=(hij)是任意n× n階上三角形矩陣.對s＞r＞0，刪去H的前r列與后n-s列及前r-1行與后n-s+1行后所得到的s-r階子矩陣稱為H的上Hessenberg子矩陣，記作Hu(r, s)=()。顯然，H的(s-r)×(s-r )階上Hessenberg子矩陣Hu(r, s)具有如下形式：

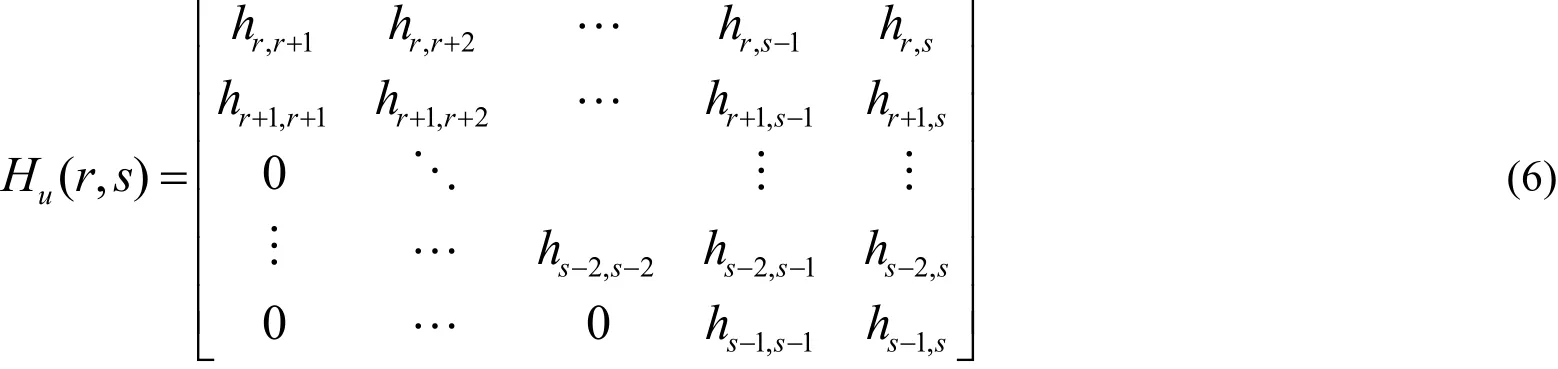
類似地，設(shè)H=(hij)是任意n× n階下三角形矩陣。對r＞s＞0，刪去H的前r行與后n-s行及前r-1列與后n-s+1列后所得到的r-s階子矩陣稱為H的下Hessenberg子矩陣,記作.顯然,H的(r-s)×(r-s )階下Hessenberg子矩陣Hl( r, s)具有如下形式：

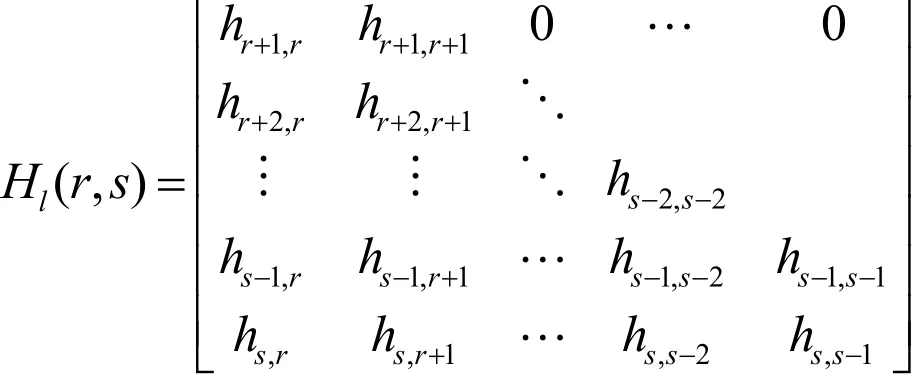
引理1設(shè)(j-i)×(j-i )階上Hessenberg矩陣Hu(i, j)由(6)所定義，則對j＞i+1，有

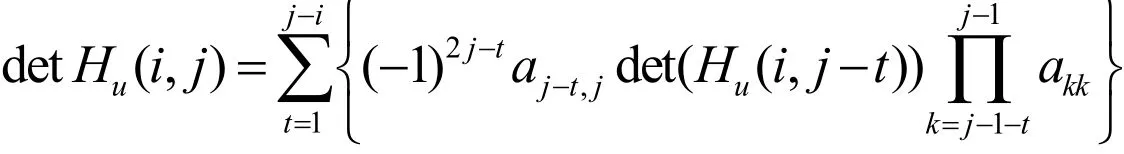
證明只需對最后一列用Laplace展開定理計算上Hessenberg矩陣Hu(i, j)的行列式即可，證畢。

定理2設(shè)U=(aij)是任意n× n階上三角形矩陣.若W=(wij)=U-1是它的逆矩陣，則

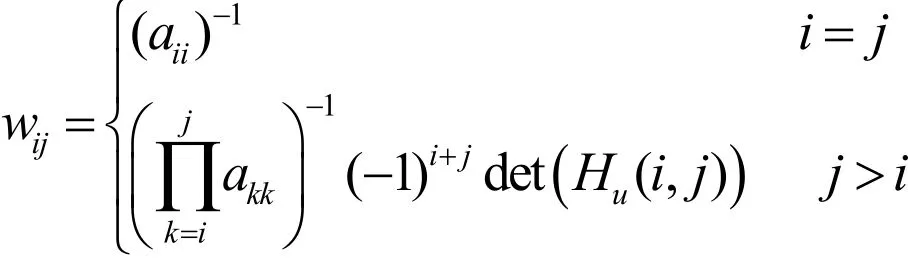
其中Hu(r, s)如前所述。

證明設(shè)WU=E=(eij)，顯然，當(dāng)i=j時，E=In是n階單位矩陣.當(dāng)j＞i時，由矩陣W和U的定義，可得：

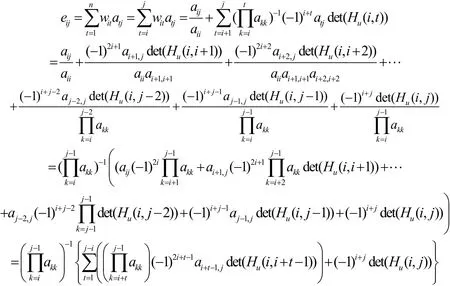
由引理1，可得eij=0，證畢。

4 r-帶狀矩陣的求逆公式

為獲得r-帶狀矩陣的求逆公式，只需求出下三角形矩陣L和上三角形矩陣U的逆即可。為此，由定理2可得引理2和引理3。因它們的證明只需代入直接驗證,故在此省略。

引理2已知下三角形矩陣L由(4)給出.若E=(eij)表示L的逆，則：其中Ll( i, j)如前所定義。

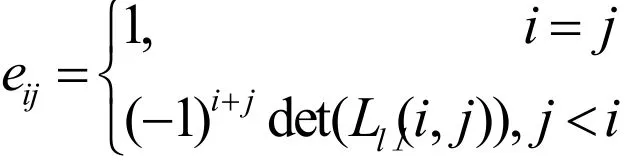
引理3已知上三角形矩陣U由(5)給出。若G=(gij)表示U的逆，則：

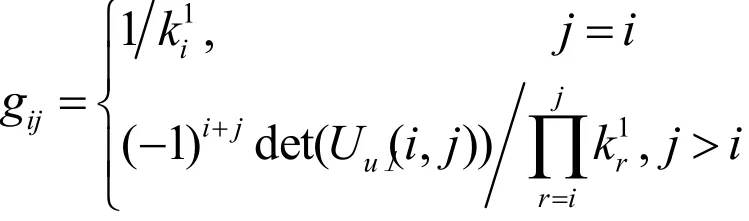
其中Uu(i, j)如前所定義。

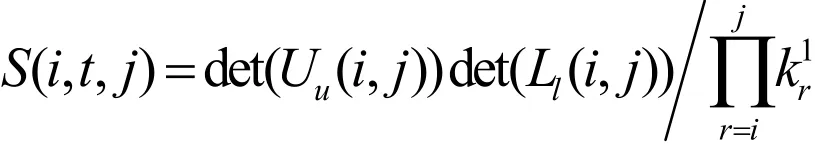
則：

證明：因為,rnBLU=，由引理2、3，可得別取i＜j, i=j, i＞j 三種情況，并將引理2、3中g(shù)it,etj的表達(dá)式代入驗證即可得證，證畢。

[1]趙立群.一些稀疏矩陣的逆和行列式的計算[D].福建:閩南師范大學(xué)數(shù)學(xué)與統(tǒng)計學(xué)院,2011

[2]陳芳,徐仲,陸全.分塊帶狀矩陣的逆[J].高等學(xué)校計算數(shù)學(xué)學(xué)報,2006,28(3):209-215

[3]楊明順.三角矩陣求逆的一種方法[J].渭南師范學(xué)院學(xué)報,2003,18(5):12-13

[4]蘇連存.高階矩陣分塊求逆的一組公式及應(yīng)用[J].青海大學(xué)學(xué)報(自然科學(xué)版),2002,20(5):62-65

[5]王美蓮,何翠竹.一類特殊矩陣的逆矩陣的特點及求逆公式[J].忻州師范學(xué)院學(xué)報,2010,26(2):42-43

[6]H B Li,Huang T Z.On the inverses of general tridiagonal matrices[J].Linear AlgebraAppl,2010,433(5):965-983

[7]Mikkawy M E,Karawia A.Inversion of general tridiagonal matrices[J].Appl Math Lett,2006,19(4):712-720

[8]Kilic E.Explicit formula for the inverse of a tridiagonal matrix by backward continued fractions[J].Appl Math Compute,2008,197(6):345-357

[9]呂小光.關(guān)于Toeplitz矩陣的計算[D].成都:電子科技大學(xué)數(shù)學(xué)科學(xué)學(xué)院,2007

[10]Mallik R K.The inverse of a tridiagonal matrix[J].Linear AlgebraAppl,2001,325(2):109-139

The Inverse Problems Research ofArbitrary Banded Matrix

DENG Yong
Department of Mathematics,Kashgar Teacher's College,Kashgar844006,China

The inverses ofr-banded matrices,forr=1,2,3 have been completely resolved as one can see from the references. LetBr,n,(1≤r≤n)be ann×nmatrix of entries{aij},(-r≤i≤r,1≤j≤r),with the remaining un-indexed entries all zeros.In this paper, generalizing a method of Mallik,we give theLUfactorization and the inverse of the matrixBr,n(if it exists).Our results are valid for an arbitrary square matrix(takingr=n),and so,we will give a new approach for computing the inverse of an invertible square matrix.

Triangular matrix;Hessenberg matrix;inverse matrix;r-banded matrix

O151.21

A

1000-2324(2014)04-0620-06

2013-03-22

2013-04-25

國家社科基金項目(11XTJ001)

鄧勇(1967-),男,四川遂寧人,教授,碩士生導(dǎo)師,主要從事矩陣及其數(shù)值研究.Email:dengy-ks@sohu.com