新安江模型參數的線性化率定

趙麗平，包為民，張 坤

1.河海大學水文水資源與水利工程科學國家重點實驗室，南京 210098 2.河海大學水文水資源學院， 南京 210098

新安江模型參數的線性化率定

趙麗平1,2，包為民1,2，張 坤1,2

1.河海大學水文水資源與水利工程科學國家重點實驗室，南京 210098 2.河海大學水文水資源學院， 南京 210098

為了解決一般概念性水文模型參數率定結果不穩定的問題，以新安江模型為例，提出了新安江模型日模參數的線性化率定方法。首先通過理想模型將該方法與SCE-UA方法及單純形方法進行對比研究。率定結果中3種算法所獲得的平均目標函數值分別為0.02、0.10、8.39 m3/s，平均循環次數分別為8、637、327，而且由線性化率定方法所獲得的各參數值方差也要比其他2種方法小得多；說明線性化率定方法能夠找到參數真值，計算精度和效率更高，率定結果更穩定。然后采用建陽和長灘河2個流域的實測資料對該方法進行應用檢驗，結果表明，同樣可以較快地率定出穩定的模型參數優值。建陽流域的10組率定結果的目標函數值皆為100.35 m3/s，循環次數也皆在8次以內，而且2個流域檢驗期的徑流深相對誤差皆在9.68%以內，確定性系數皆在0.819以上。因此，線性化參數率定方法確實能夠解決非線性模型參數率定結果不穩定的問題，不會產生不相關的局部參數優值，并且不受參數初值影響，計算精度高，循環次數少，是一種可行有效的全局優值參數優選方法。

參數優選；線性化參數率定方法；新安江模型；日模

0 引言

流域水文模型在進行水文規律研究和解決生產實際問題中起著重要的作用，其由模型結構和模型參數共同組成，在模型結構確定后，模型參數的確定就顯得尤為重要，模型模擬得好壞很大程度上依賴于模型參數的選擇[1]。目前參數優選的手段可分為2類：人工優選(試錯法)和自動優選。人工試錯法因耗時耗力，受人為主觀因素影響，傳承性不高；自動優選不僅可以節約人力物力、降低模型使用成本，而且有利于模型的進一步推廣應用。模型參數自動優選方法可以分為傳統優化算法與現代優化算法：傳統優化算法包括單純形方法[2]、Rosenbrock法[3]、Powell法[4]、Newton法[5]等，它們都是與初始點有關的局部優化方法，常常是找出初始點附近的一個極值點，不同的初始點往往獲得不同的結果，不能保證獲得的為全局優值；現代優化算法包括模擬退火法[6]、SCE-UA算法[7]、遺傳算法[8-10]、粒子群優化方法[11]、人工神經網絡算法[12]等，這些方法以尋找全局優值為出發點，構建確定性尋找信息與隨機相結合的率定方法，試圖避免傳統方法存在的問題，以得到全局最優的、唯一的參數估計，但該類方法同樣無法證明所獲得的參數值是否為全局最優，甚至連參數估計方法本身的收斂性也常難以證明，只在概率意義上分析能收斂于全局優值。

包為民[13-14]在20世紀80年代就提出，現有參數估計方法的根本問題在于目標函數的黑箱子結構和基于目標函數的信息利用方法。迄今為止，大多數目標函數還是沿用傳統的誤差平方和形式，以此作為確定參數的信息依據[13,15]，通常包括構建誤差平方和目標函數與一階函數求導為0得參數優值解兩步操作。這一做法對于線性參數的率定沒有任何問題，可以得到唯一解，但在率定非線性函數參數時，會增加不相關的局部參數優值解，致使參數率定結果不穩定；為此包為民等[16]提出了非線性函數參數的線性化率定方法，解決了額外增加不相關局部優值的理論性問題，并證明了該方法的收斂性，同時檢驗了其合理性。筆者將這一新的參數率定方法與新安江模型結合，首先利用理想模型將該方法與SCE-UA方法及單純形方法進行對比研究，驗證該方法的可行性，然后再將其運用到2個實測流域進行應用檢驗。

1 非線性參數的線性化率定方法

1.1 線性化參數率定方法的基本原理

針對一般參數為n次的非線性函數f=x+θx+(θx)2+…+(θx)n,n≥2(θ為參數，x為自變量向量)，若{xi，fi，i=1，2，…，L}(L為觀測樣本總數目)為其觀測樣本，則誤差平方和目標函數為

(1)

對其參數一階求導后得：

(2)

令其為0便會得到2n-1個解，增加了n-1個不相關的局部參數優值。然而對線性參數不存在這種問題，因此一個自然的想法就是先把非線性參數函數以參數作為自變量進行線性化，即進行一階泰勒展開，使非線性參數率定問題轉化為線性參數率定問題，然后再以誤差平方和為目標函數進行率定，這樣便可以解決額外不相關的局部參數優值問題，整個率定過程也是一個逐步迭代逼近優值的過程。

舉例來說，假設通過線性化率定方法來率定非線性參數函數f=f(θ，xk)中的參數，其中θ為n維的參數向量，xk為第k個樣本自變量。現以參數作為自變量進行線性化(為了便于寫通式，假設率定進行到第j步)，即進行一階泰勒展開得

(3)

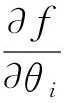
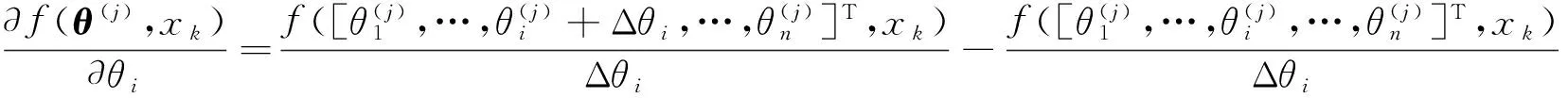
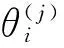
假設參數率定中有L組觀測樣本：(x1，f1)，(x2，f2)，…，(xL，fL)，代入式(3)并寫成向量矩陣形式：

(4)

式中：

S=

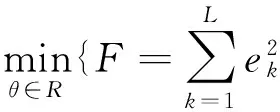
(5)

但是，式(4)只是實際函數的線性化近似，故由式(5)得出的θ(j+1)不一定為尋找方向上的最優值，還需對其進行修正，做法是乘以一個修正尺度系數b，即

(6)

從而使得實際誤差函數在尋找方向上為最優的。系數b的取值范圍為(0，1),可根據計算值與實際值的誤差平方和最小確定：

(7)

從而，線性化參數率定方法根據式(5)確定參數尋找方向，根據式(6)和(7)確定參數變化步長，這樣既確保了尋找方向的正確性又使得尋找方向上的誤差最小。

1.2 線性化參數率定方法的基本步驟

由于該率定方法是基于對實際函數的線性化近似，必然存在誤差，故使用其率定參數的過程也是一個逐步循環迭代逼近參數優值的過程，具體計算流程可用圖1表示。

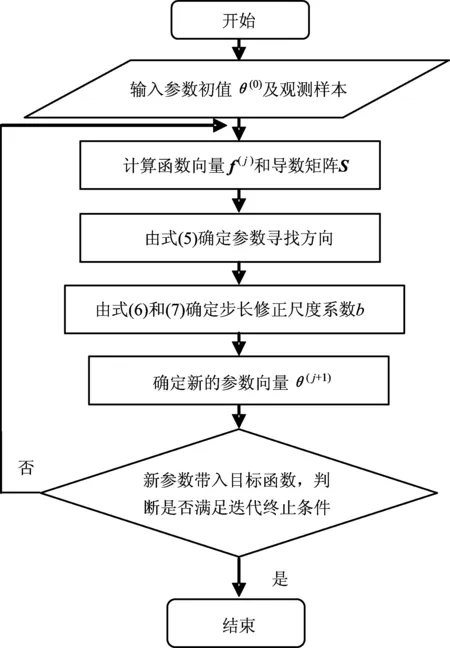
圖1 線性化參數率定方法流程圖Fig.1 Flowchart of the linearized calibration method

本文所采用的目標函數為均方根誤差(root mean square error)：

(8)

式中：Qob(i)為實測流量序列；Qc(i)為計算流量序列。

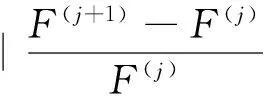
2 新安江模型簡介

新安江模型是由河海大學趙人俊教授[17]所提出的，廣泛地適用于我國濕潤及半濕潤地區。該模型考慮了降雨及下墊面分布的不均勻性，首先將流域劃分成若干個子單元，對每個子單元進行蒸散發、產流、分水源和匯流計算，得到單元流域出口流量過程；然后再進行單元流域出口以下的河道匯流計算，得到該單元流域在全流域出口斷面的流量過程；最后將每個單元流域在全流域出口斷面的流量過程進行線性疊加，得到全流域總的出口流量過程。在本文中，蒸散發計算采用三層蒸發模型；產流計算采用蓄滿產流計算模型；分水源采用自由水蓄水庫結構將總徑流劃分為地表徑流、壤中流和地下徑流3種成分；坡面匯流采用線性水庫進行計算；河道匯流采用馬斯京根法。

模型中共包括15個參數。蒸散發計算參數：流域蒸散發折算系數K，上層張力水容量UM，下層張力水容量LM，深層蒸散發折算系數C；產流參數：流域平均張力水容量WM，張力水蓄水容量曲線方次B；分水源參數有表層自由水蓄水容量SM，表層自由水蓄水容量曲線方次EX，表層自由水蓄水庫對地下水的日出流系數KG，表層自由水蓄水庫對壤中流的日出流系數KI；匯流參數：地表徑流消退系數CS，壤中流消退系數CI，地下徑流消退系數CG；馬斯京根法的2個演算參數：KE和XE。其中，敏感參數有9個，分別是K，SM，KI，KG，CS，CI，CG，KE，XE。由于本文所使用的資料是基于日尺度的，所以KE與XE也表現為相對不敏感。不敏感參數可通過一般經驗和流域特性而確定，不必參與優選。另外，為了解決水源劃分中參數不獨立的問題，根據壤中流退水歷時一般為3 d左右，采用結構約束KI+KG=0.7。因此，本文暫且只對K，SM，KG，CS，CI，CG這6個敏感參數進行優選研究。

3 實例應用

3.1 實驗流域簡介

所選研究區域為建陽流域與長灘河流域。建陽流域面積為4 848 km2，屬于閩江干流上的一個子流域，地處亞熱帶季風氣候區，氣候溫和，雨量充沛，多年平均降水量為1 400～2 400 mm，多年平均蒸發量為915 mm，所采用的資料是該流域1986-2000年逐日降雨、逐日蒸發及逐日流量資料；長灘河流域面積為2 034 km2，地處亞熱帶濕潤季風氣候區，季風氣候明顯，呈現冬無嚴寒、夏無酷暑、暖濕多雨的特點，年平均氣溫為16～18 ℃，暴雨多于6-9月份出現，多年平均降雨量約1 200 mm，徑流主要靠降雨補給，其變化趨勢與降雨一致，所采用的資料是該流域1974-1986年的逐日資料。

3.2 理想模型驗證

為了驗證線性化參數率定方法的可行性和有效性，采用理想模型對該方法與SCE-UA方法[7]及單純形方法[18]進行了對比分析研究。所謂理想模型是指模型參數、輸入、輸出及誤差皆為已知的模型。先給定一組模型參數值，即理想模型參數真值(表1)；再利用建陽流域1986-2000年的逐日降雨和蒸發資料與新安江模型進行出口斷面的流量計算，以計算的流量作為理想實測流量；即生成無誤差的理想模型。

表2、表3及表4分別列出了10組不同參數初值的3種方法率定結果，從表2-表4可以看出：

1)比較方差可知：隨機生成的參數初值對線性化參數率定結果影響最小，率定結果最穩定；SCE-UA方法次之；而對單純形方法影響較大，率定結果不穩定。

表1 理想模型參數真值

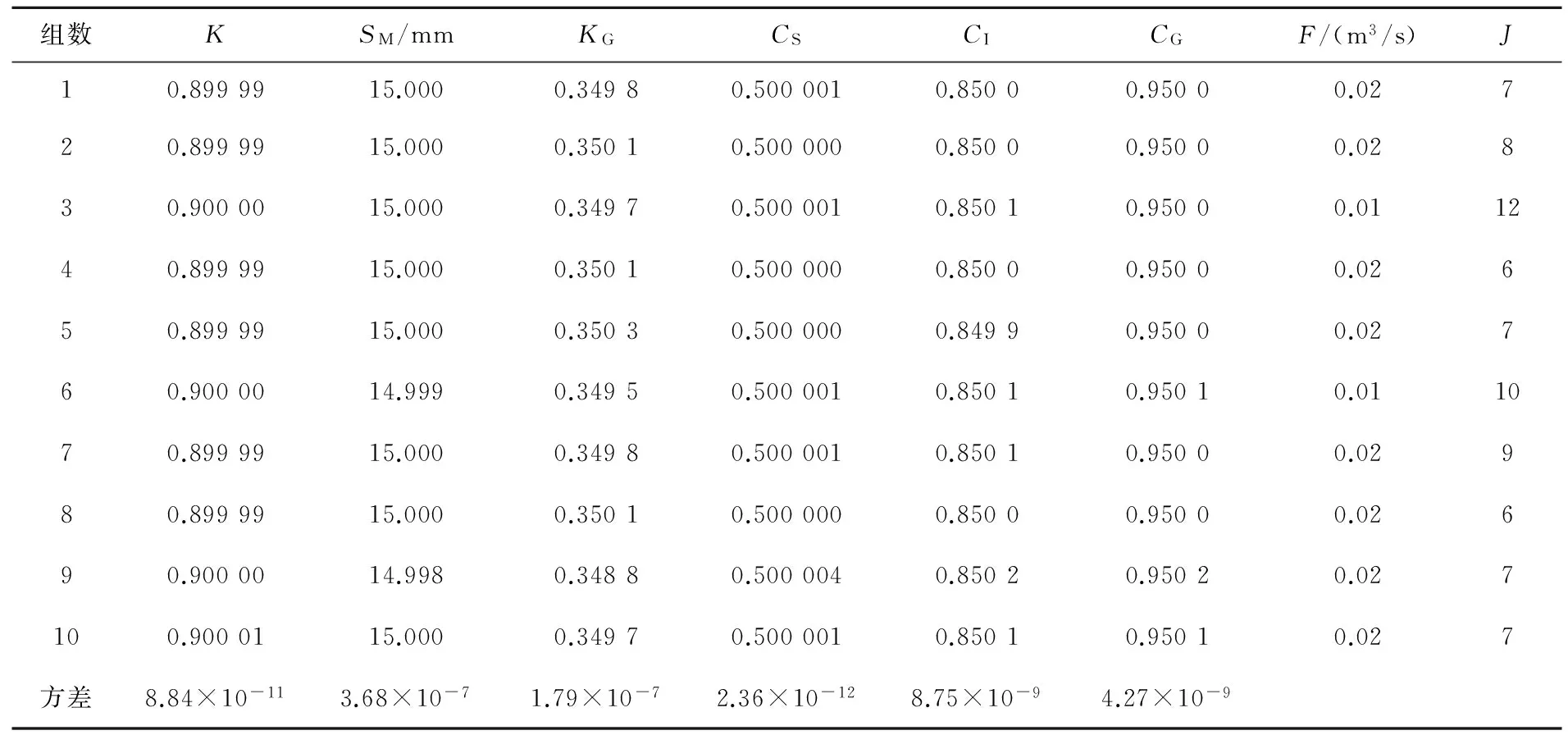
表2 不同參數初值的線性化方法率定結果

注:J為每組初值尋找優值的循環次數，下同。

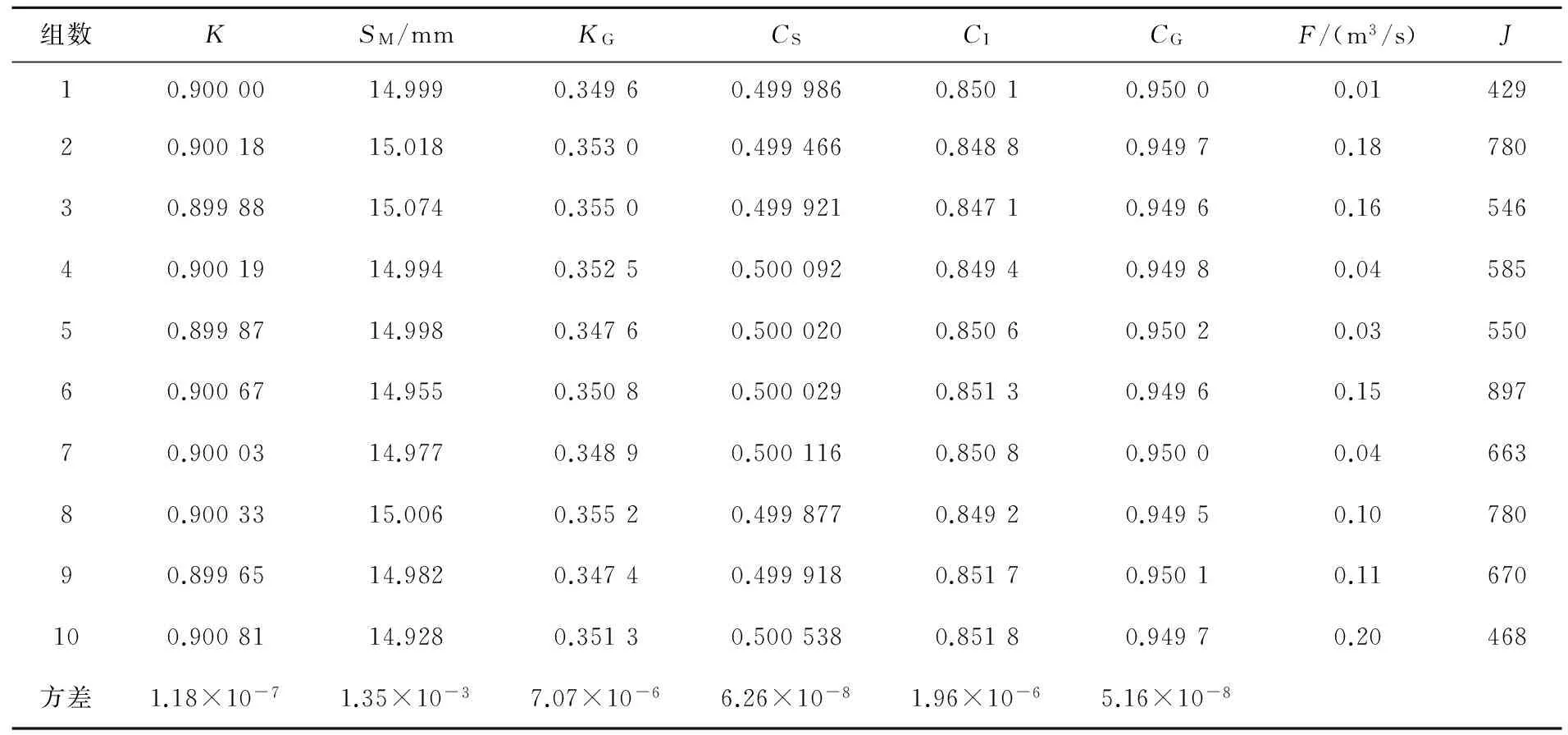
表3 不同參數初值的SCE-UA方法率定結果

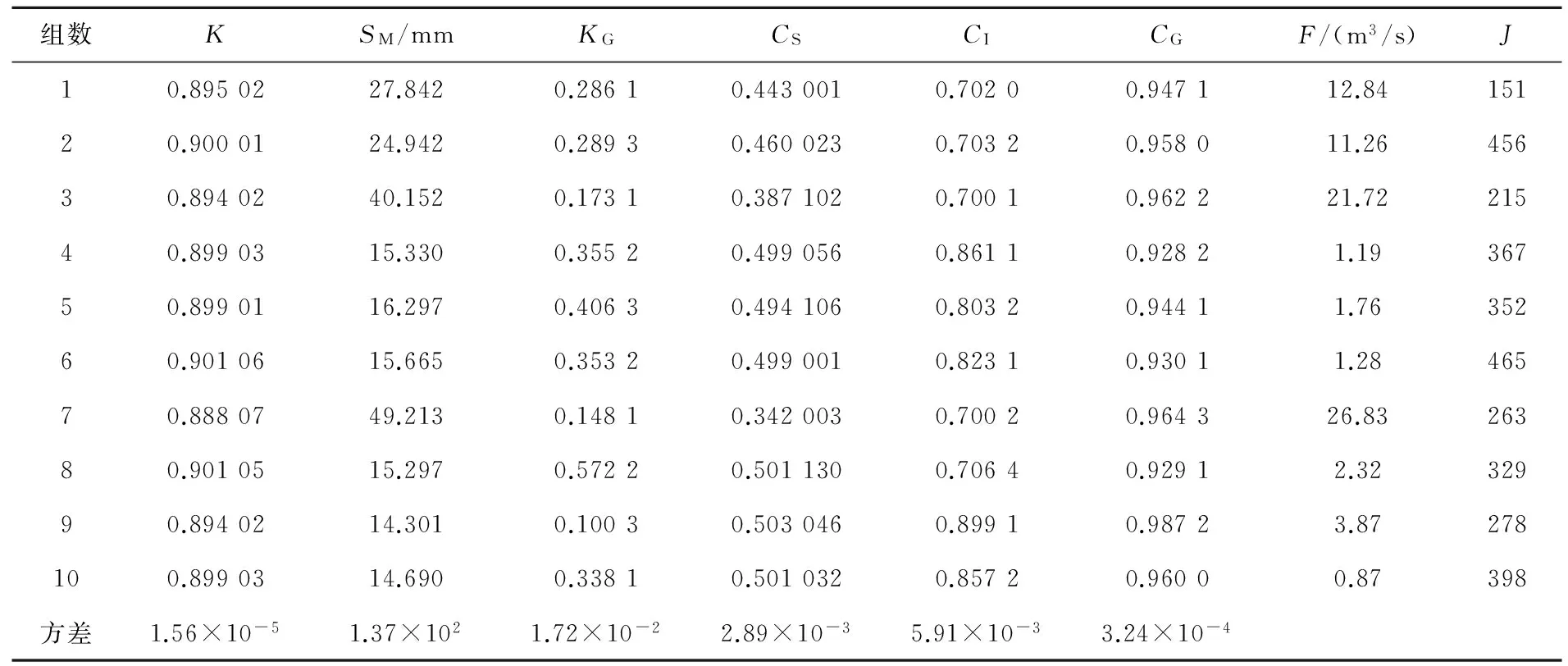
表4 不同參數初值的單純形方法率定結果

2)比較F可知：線性化參數率定方法客觀并且計算精度最高；SCE-UA方法次之；單純形方法計算精度最低。在線性化率定方法中，各參數率定結果均可以認為已經率定到“參數真值”，而且誤差目標函數值很小，取值為0.01 m3/s或0.02 m3/s；SCE-UA方法的率定結果也可以認為已經率定到“參數真值”，但計算精度略差于線性化率定方法，誤差目標函數值最小為0.01 m3/s，最大為0.20 m3/s，平均值為0.10 m3/s；而在單純形方法率定結果中，各參數與“參數真值”差別較大，誤差目標函數值也很大，最大為26.83 m3/s，最小為0.87 m3/s，平均值為8.39 m3/s。

3)比較J可知：線性化率定方法循環次數最少，率定效率最高；單純形方法次之；SCE-UA方法最慢。10組率定結果中：采用線性化率定方法，最少的只要6次便找到了優值，最多的也只需12次，平均值為8；采用單純形方法，最少的需要151次，最多的需要465次，平均值為327；而采用SCE-UA方法最少需要429次，最多需要897次，平均值為637。

圖2展示了10組不同初始值下，3種優化算法的精度(最終目標函數值)與效率(循環次數)；圖3則展示了對于第1組參數初值采用3種方法率定時，目標函數值的具體變化情況。從圖2可以明顯地看出：無論計算精度還是效率，線性化率定方法都明顯優于其他2種方法；由于線性化率定方法10組率定結果的目標函數值與循環次數都較小而且差別不大，所以10個點幾乎重疊在一起，這也說明了率定結果穩定，沒有出現不唯一的現象。從圖3可以看出：線性化率定方法收斂速度最快，整個率定過程只需要7步循環，循環進行到第3步時，目標函數值就已經變得很小，說明線性化參數率定方法可以準確地確定尋優方向，收斂性能較好，計算精度較高；而SCE-UA方法與單純形方法則都需上百次循環迭代，尤其是SCE-UA方法更慢，但其計算精度要高于單純形方法；單純形方法是一種單點迭代式尋優方法，很容易陷入局部優值，計算精度無法令人滿意。

圖2 3種算法的循環次數與目標函數變化圖Fig.2 Objective function value versus iteration numbers

綜上來說，線性化參數率定方法確實解決了模型參數率定結果不穩定的問題：對于穩定性與計算精度線性化率定方法都是最好的，SCE-UA方法次之，單純形方法最差；對于計算效率，依然是線性化率定方法最快，單純形方法次之，SCE-UA方法最慢。因此，線性化參數率定方法是一種可行有效的參數優選方法，可以運用到基于實測資料的新安江模型參數率定中。

3.3 采用實測資料的參數率定

3.3.1 基于建陽流域實測資料的參數率定

采用建陽流域1986-1995年的逐日實測蒸發、降雨及流量資料用于參數率定(表5)，這里也只是對6個較敏感參數進行自動率定，該流域其他不敏感參數取值情況同表1。表5列出了10組不同的參數初值的日模率定結果，每一行即為一組。從表中結果可以看出：10組不同的參數初值下，率定結果相當穩定，各參數分別穩定在1.092 53、44.681、0.405 7、0.384 706、0.700 3、0.987 3左右，誤差目標函數值F都為100.35 m3/s，沒有出現率定結果不唯一的現象，各參數也都在物理意義合理的范圍內，而且循環次數少，率定效率高。

用1996-2000年的實測資料對率定出的參數結果進行檢驗，檢驗結果見表6。從表6中可知：5年檢驗期中，徑流深相對誤差都在9.68%以內，平均相對誤差為4.08%；確定性系數都在0.898以上，平均確定性系數為0.900。這說明采用線性化方法率定出的參數是合理的。

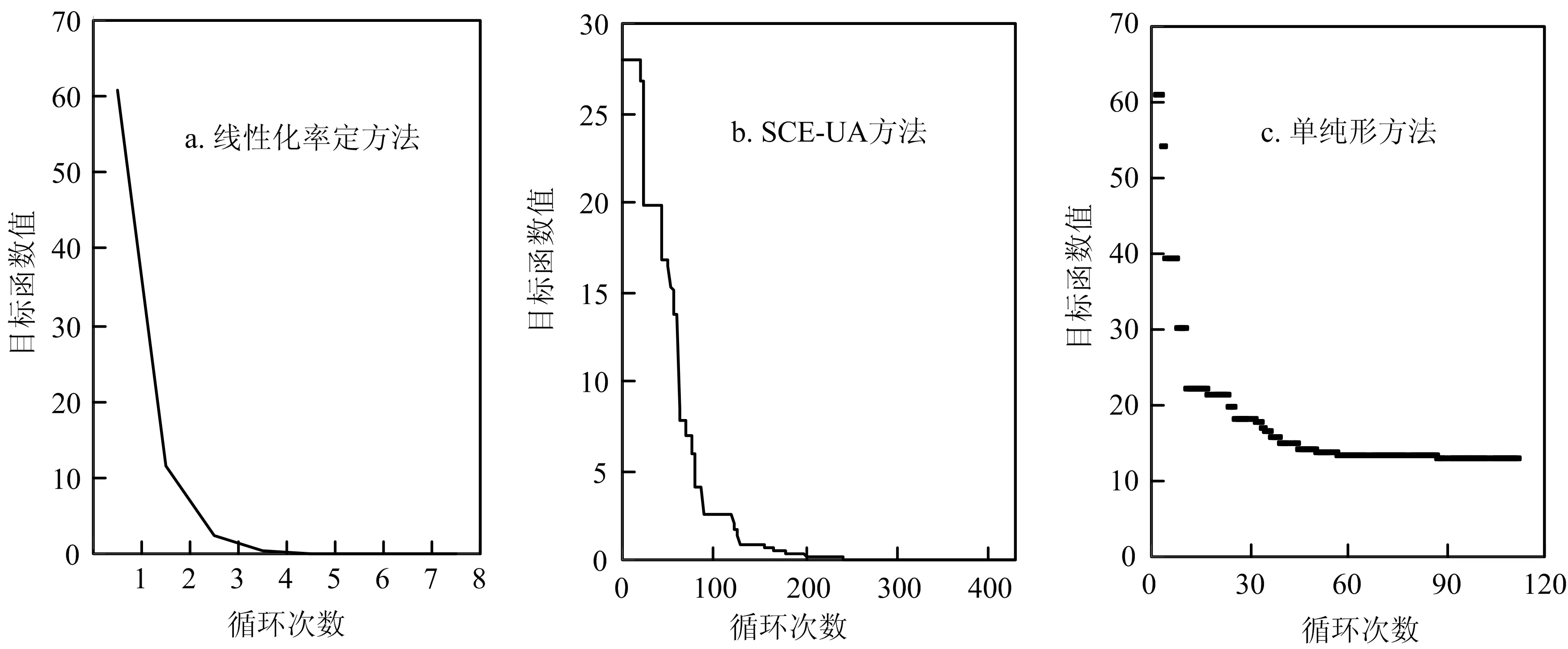
圖3 不同方法的第1組數據目標函數變化圖Fig.3 Objective function change of the first run for the three different methods

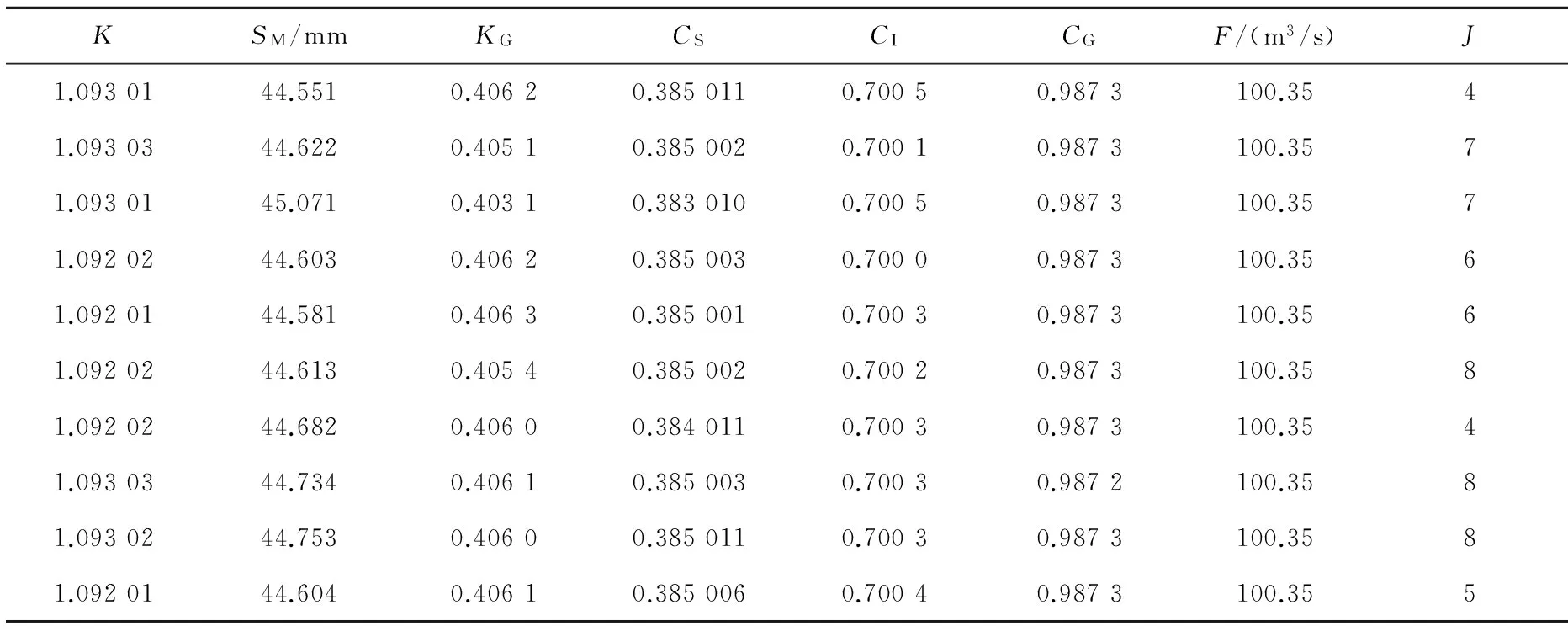
KSM/mmKGCSCICGF/(m3/s)J1.0930144.5510.40620.3850110.70050.9873100.3541.0930344.6220.40510.3850020.70010.9873100.3571.0930145.0710.40310.3830100.70050.9873100.3571.0920244.6030.40620.3850030.70000.9873100.3561.0920144.5810.40630.3850010.70030.9873100.3561.0920244.6130.40540.3850020.70020.9873100.3581.0920244.6820.40600.3840110.70030.9873100.3541.0930344.7340.40610.3850030.70030.9872100.3581.0930244.7530.40600.3850110.70030.9873100.3581.0920144.6040.40610.3850060.70040.9873100.355

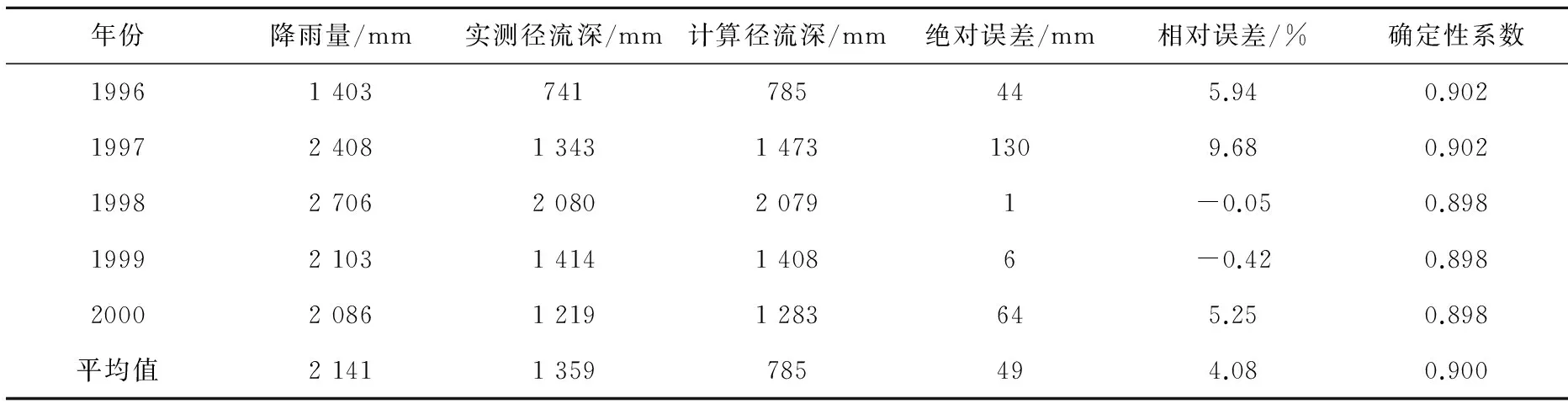
表6 建陽流域檢驗結果

表7 長灘河流域檢驗結果

3.3.2 基于長灘河流域實測資料的參數率定

采用線性化率定方法對長灘河流域1974-1983年的逐日資料進行6個較敏感參數的自動率定(其他不敏感參數按物理意義及流域特性取值)。對于隨機生成的10組參數初值，參數率定結果也是基本一致，K、SM、KG、CS、CI、CG6個參數分別為0.636 01、13.182、0.222 1、0.248 003、0.717 2、0.950 1，并且也都在物理意義合理的范圍內。對率定出的參數結果再用1984-1986年的實測資料進行檢驗，檢驗結果見表7。由表7可知：3年檢驗期中，徑流深相對誤差都在2.77%以內，平均相對誤差為0.55%；確定性系數都在0.819以上，平均確定性系數為0.823。

由以上2個實際流域的應用檢驗可以看出，線性化參數率定方法具有較好的實際應用效果，率定結果穩定，不受參數初值影響，收斂速度快，計算精度高，從而為水文模型又尋找到了一種較好的參數率定方法。

4 結論

基于一般概念性水文模型參數率定結果不穩定的問題提出了新安江模型參數的線性化率定方法，通過理想模型與SCE-UA方法及單純形方法進行對比分析以及實際流域的應用檢驗可知：

1)線性化參數率定方法有效地解決了非線性模型參數率定結果不穩定的問題，其原理簡單，結構合理，易于編程。

2)無論計算精度，效率還是穩定性，線性化參數率定方法都優于SCE-UA方法及單純形方法，具有計算精度高、循環次數少、率定結果穩定、不受初值影響等優點，是一種可行有效的全局優值參數優選方法。

3)該方法在實際應用中取得了較好的效果因而具有一定的應用價值，而且對其他模型參數優選也具有一定的借鑒意義。但本文僅討論了線性化參數率定方法對新安江日模敏感參數的優選，若不敏感參數也參加優選，不僅參數維數增多，參數敏感度降低，而且參數之間的相關性也更復雜，可能會影響參數率定效率與精度，因此下一步計劃對不敏感參數以及次洪參數優選進行深入研究。此外本文只是對于2個流域進行了分析應用，若要推廣應用還需更多流域進行驗證分析。

[1] Ng A W M, Perera B J C. Selection of Genetic Algorithm Operations for River Water Quality Model Calibration[J]. Engineering Application of Artificial Intelligence, 2003,16(5):529-541.

[2] 丁杰，何建華，謝紅英，等.基于單純形法的新安江次洪模型的參數優化研究[J].水電能源科學，2010，28(11)：18-20. Ding Jie, He Jianhua, Xie Hongying, et al. Application of Simplex Method to Parameter Calibration of Xin’anjiang Model[J]. Water Resources and Power, 2010, 28(11):18-20.

[3] Rosenbrock H H.An Automatic Method for Finding the Greatest or Least Value of a Function[J].Compu-ter Journal,1960,3:175-184.

[4] Powell M J D. An Efficient Method for Finding Minimum of a Function of Several Variables Without Calculating Derivatives[J].Computer Journal, 1964, 7:155-162.

[5] Hendrickson J D, Sorooshian S, Brazil L E. Comparison of Newton-Type and Direct Search Algorithms for Conceptual Rainfall-Runoff Models[J].Water Resources Research,1988,24(5):691-700.

[6] Vandewiele G, Xu Chongyu, Huybrechts W, et al. Methodology and Comparative Study of Monthly Water Balance Models in Belgium, China and Burma[J].Journal of Hydrology,1992,134:315-347.

[7] Duan Q, Sorooshian S, Gupta V. Effective and Efficient Global Optimization for Conceptual Rainfall-Runoff Models[J] .Water Resources Research, 1992, 28(4):1015-1031.

[8] 譚炳卿.水文模型參數自動優選方法的比較分析[J].水文，1996，16(5)：58-65. Tan Bingqing. A Comparative Study on Optimization Methods for Calibrating the Hydrological Models[J]. Hydrology, 1996, 16(5):58-65.

[9] 殷文，印興耀，張繁昌.基于并行遺傳算法的地震屬性優化研究[J].吉林大學學報：地球科學版，2005，35(5)：672-676. Yin Wen, Yin Xingyao, Zhang Fanchang. A Study on Seismic Attribute Optimization Based on Parallel Genetic Algorithm[J]. Journal of Jilin University: Earth Science Edition, 2005, 35(5): 672-676.

[10] 李鴻雁，趙娟，王玉新，等. 擴域搜索遺傳算法優化馬斯京根參數及其應用[J].吉林大學學報：地球科學版，2011，41(3)： 861-865. Li Hongyan,Zhao Juan,Wang Yuxin,et al.Muskingum Parameter Optimization Through Extension Field Search Genetic Algorithm and Its Application[J]. Journal of Jilin University: Earth Science Edition, 2011, 41(3): 861-865.

[11] 江燕，胡鐵松，桂發亮，等.粒子群算法在新安江模型參數優選中的應用[J].武漢大學學報：工學版，2006，39(4)：14-17，24. Jiang Yan, Hu Tiesong, Gui Faliang, et al. Application of Particle Swarm Optimization to Parameter Ca-libration of Xin’anjiang Model[J]. Engineering Journal of Wuhan University, 2006, 39(4):14-17,24.

[12] Hopfield J, Tank D. ‘Neural’ Computation of Derisions in Optimization Problems[J] .Biological Cybernetics, 1985, 52:141-152.

[13] 包為民. 模型參數估計研究[D].南京：河海大學，1989. Bao Weimin. The Research About Calibrating Model Parameters[D]. Nanjing: Hohai University,1989.

[14] 包為民.新安江模型參數的自動率定[J].河海大學學報：自然科學版，1986(4)：22-30. Bao Weimin. Automatic Calibration of Xing’anjiang Model Parameters[J]. Journal of Hohai University: Natural Sciences Edition, 1986(4): 22-30.

[15] 楊曉華，楊志峰，酈建強，等. 水文模型參數識別算法研究及展望[J].自然科學進展，2006，16(6)：657-661. Yang Xiaohua, Yang Zhifeng, Li Jianqiang, et al. The Research and Prospect About Hydrological Model Parameter Identification Algorithm[J].Progress in Natural Science, 2006, 16(6):657-661.

[16] 包為民，司偉，瞿思敏. 非線性參數的線性化率定方法[J]. 計算力學學報，2013，30(2)：236-241. Bao Weimin, Si Wei, Qu Simin. The Linearized Calibration Method of Nonlinear Function Parameter[J]. Chinese Journal of Computational Mechanics, 2013, 30(2):236-241.

[17] 趙人俊. 流域水文模擬：新安江模型與陜北模型[M].北京：水利電力出版社，1984. Zhao Renjun. Watershed Hydrological Simulation: Xin’anjiang Model and Shanbei Model[M]. Beijing: Water Power Press, 1984.

[18] Nelder J A, Mead R. A Simplex Method for Function Minimization[J].Computer Journal, 1965, 7(2):308-313.

Linearized Calibration of Xin’anjiang Model Parameters

Zhao Liping1,2, Bao Weimin1,2,Zhang Kun1,2

1.StateKeyLaboratoryofHydrologyWaterResourcesandHydraulicEngineering,HohaiUniversity,Nanjing210098,China2.CollegeofHydrologyandWaterResources,HohaiUniversity,Nanjing210098,China

In order to solve the problem of unstable parameter calibration results of conceptual hydrological model, the linearized calibration method of Xin’anjiang daily model parameters was put forward. Firstly, this method was compared with the SCE-UA method and the Simplex method through an ideal model. The average values of objective function obtained by the 3 methods were 0.02, 0.10 and 8.39 m3/s, respectively and the average iteration numbers were 8, 637 and 327, respectively. Moreover, the parameter variances obtained by the linearized calibration method were much smaller than those of other two methods. These results demonstrated that the linearized calibration method can find the true parameter values. It also has higher accuracy and convergence speed with more stable calibration results. Then the performance of the new method in model parameter calibration was examined using the measured data of Jianyang and Changtan River basin. The results showed that the stable optimal parameter values could also be quickly got. All of the objective function values of the 10 runs in Jianyang River basin were 100.35 m3/s and the iteration numbers were all within 8. In the validation phase of the two river basins, the relative errors of runoff depth were all within 9.68% and the values of determination coefficient were all above 0.819. It can be concluded that the linearized calibration method can solve the problem of unstable calibration results about nonlinear model parameters without producing unrelated local optima. Furthermore, it is not influenced by the different initial parameter values and has high computation accuracy and needs small iteration numbers. Hence, the linearized calibration method is an effective global optimization method.

parameter optimization; linearized calibration method; Xin’anjiang model; daily model

10.13278/j.cnki.jjuese.201401208.

2013-07-16

國家自然科學基金項目(51279057)；國家自然科學基金重大項目(51190090)；中國國家重點實驗室專項基金項目(2009585412)；中央高校基礎研究基金項目(B1020072)

趙麗平(1989-)，女，博士研究生，主要從事水文預報及模擬方面的研究，E-mail:zhaoliping_ok@126.com

包為民(1956-)，男，教授，博士，主要從事水文預報及模擬方面的研究，E-mail:wmbao163@163.com。

10.13278/j.cnki.jjuese.201401208

P338

A

趙麗平，包為民，張坤.新安江模型參數的線性化率定.吉林大學學報:地球科學版,2014,44(1):301-309.

Zhao Liping,Bao Weimin,Zhang Kun.Linearized Calibration of Xin’anjiang Model Parameters.Journal of Jilin University:Earth Science Edition,2014,44(1):301-309.doi:10.13278/j.cnki.jjuese.201401208.