用數學建模解決身邊的經濟問題案例及分析
●姜文彪
用數學建模解決身邊的經濟問題案例及分析
●姜文彪
數學建模課程對數學素質的要求比較高,尤其是經濟、管理類專業的學生對本門課程學習起來更是感覺困難,實際生活中難以應用。在經濟數學的教學中融入數學建模的思想,使數學建模與經濟數學、實際問題有機地結合起來,讓數學變得既生動又符合實際,取得良好的教學效果。
數學建模 經濟數學 貨幣流 循環經濟
一、引言
數學建模是在20世紀60~70年代進入西方國家一些大學的,我國的幾所大學也在80年代初將數學建模引入課堂。經過30多年的發展,現在絕大多數本科院校和許多專科學校都開設了各種形式的數學建模課程和講座,我校也在1996年開設了數學建模課程,同年開始參加全國大學生數學建模競賽。經過近20年的建設,數學建模課程已被評為校級精品課,越來越多的學生也開始對數學建模這門課程產生了興趣。但這門課程對數學素質的要求比較高,很多學生在學習中很難理解和接受,尤其經濟、管理類專業的學生,覺得這門課程枯燥乏味,晦澀難懂,和本專業好像聯系不大,從而產生厭學思想。本文根據筆者多年教學實踐和探索,將身邊的經濟問題轉化為數學問題,建立數學模型,用數學方法加以解決,讓學生對數學建模產生興趣,在講解經濟數學的同時掌握了常見的數學建模方法,這樣極大地提高了學生學習數學的興趣,取得了較好的教學效果。
二、教學案例
(一)是買還是租
隨著人們生活水平的提高,越來越多的人們開始擁有了私家車,隨著買車市場的繁榮,租車市場也日漸興起。那么,到底是買車劃算還是租車劃算呢,下面我們用建模的思想對此問題加以解決。
假設購買一輛家用汽車需要15萬元現金,使用壽命15年;如果租一輛汽車,每年需要支付1.5萬元租金,租金以貨幣流的方式支付,若銀行的年利率是4%,問購買還是租用汽車劃算,如果銀行的年利率是8%,結論又是如何呢?
分析:購買一輛汽車可以使用15年,但需要馬上支付15萬元,而同樣租一輛汽車使用15年,則需要以貨幣流的方式支付15年的租金,年流量為1.5萬元。兩種方案所支付的價值無法直接比較,必須將它們都化為同一時刻的價值才可以比較。我們以當前的價值為準,購買一輛汽車的當前價格為15萬元。
下面計算均勻貨幣流的當前價格。
設t=0時向銀行存入Ae-rT元,若按連續復利計算,T年后在銀行的存款恰好為A元。那么,對流量為a的均勻貨幣流,在[t,t+△t]時所存入的元a△t元,在t=0時價值是a△tge-rt=ae-rt△t。
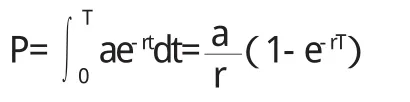
所以,15年的租金在當前的價值為:

此時租汽車比購買汽車劃算。
(二)用“循環經濟”理念制定發展規劃
制定一個地區的規劃,不同的理念將導致不同的結果,或成功或失敗。以科學發展觀為指導思想,應用循環經濟理念制定發展規劃,越來越為人們所接收。
下面用陸鐘武教授提出的基于IPAT方程的環境負荷控制模型加以分析。
IPAT方程可表達為:
I=P×A×T
此模型簡單實用,它是西方學者經過多年反復討論、經過驗證確定下來的。其中I表示環境負荷,P表示人口,A表示人均GDP,T表示單位的GDP環境負荷。例如:
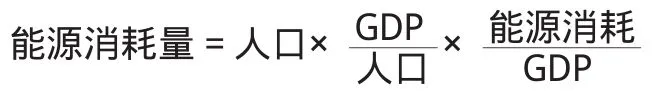
例如:設我國2013年人口為13.5×108人,人均為6000美元;2023年人口為15×108人,人均為11000美元。若此期間不允許環境負荷上升,問萬美元GDP環境負荷應降低多少?
分析:設2013年,環境負荷為I0,萬美元GDP環境負荷為T0,則:

即在此期間,萬美元GDP環境負荷應降低2.04倍。
以上是筆者在經濟數學課程教學中將數學建模融入其中的幾個教學案例,當然還有很多需要完善和改進的地方。用數學定量地解決經濟、管理科學和經濟、管理實踐中的問題,恰當地建立于這些問題有關的數學模型是關鍵。培養學生具有一定的數學素養、掌握一定的數學建模能力,對當前培養創新型和應用型人才顯得尤為重要。
[1]母麗華,周永芳.數學建模[M].科學出版社,2011
[2]彭紅軍,張偉,李媛.微積分[M].機械工業出版社,2013
[3]譚永基等.經濟管理數學模型案例教程[M].高等教育出版社,2006
[4]錢和平,徐青舟.數學建模融入經濟數學教學中的案例及分析[J].大學數學,2012(6)
(作者單位:黑龍江科技大學理學院 黑龍江哈爾濱 150022)
(責編:賈偉)
F224
A
1004-4914(2014)04-268-01

