基于射擊次數的編隊防空隊形優化配置

翁璐，姚躍亭，劉劍鋒，孟凡磊

（1.海軍裝備部，北京100841；2.海軍航空工程學院飛行器工程系，山東煙臺264001）

基于射擊次數的編隊防空隊形優化配置

翁璐1，姚躍亭2，劉劍鋒1，孟凡磊2

（1.海軍裝備部，北京100841；2.海軍航空工程學院飛行器工程系，山東煙臺264001）

為解決艦艇編隊協同防空中抗擊多方向來襲目標流的隊形部署優化問題，提出了以編隊對來襲目標流的綜合射擊次數為目標函數的優化方法。將編隊總射擊次數分解為零航路捷徑和非零航路捷徑下的射擊次數之和，利用射擊次數與、殺傷區縱深、隊形配置向量之間的約束關系，給出了計算方法。以一字隊形為例，建立了隊形部署優化模型。

編隊防空隊形優化配置；射擊次數；多方向目標流；一字隊形

在艦艇編隊協同防空中，良好的編隊隊形配置，是達到合理利用兵力、充分發揮火力、有效抗擊敵空襲的重要條件，也是實施防空射擊指揮決策的基本依托。編隊隊形配置是一個綜合多種因素、尋求最佳方案的過程。這些因素包括：防空武器數量和性能、殺傷區耦合、敵來襲方向、對抗干擾、火力掩護區面積等。單獨考慮某一個因素進行隊形配置有失偏頗，很難得到正確的結果；因素太多，會使防空隊形配置建模過程顯得非常復雜。因此，需要一個綜合性的指標，通過建立各種因素的約束關系模型，來合理準確地反映編隊隊形配置的優劣，

文獻[1]以被掩護艦的生存概率為優化目標，建立了防御隊形配置方法。但是該方法受敵我兵力使用方式影響較大。文獻[2]從電子對抗、火力協同、指揮通信和區域掩護4個方面對對象配置進行了較為完整的研究。但對一些問題闡述還不夠深入。文獻[3]給出了航母編隊防空哨戒陣位缺點原則。文獻[4]則以防空區域防御縱深最優為目標，研究了雙艦編隊的扇面部署問題。但是航母編隊往往規模較大，而雙艦編隊則規模太小，兩者的研究成果都很難直接應用在常規驅護艦編隊的防空隊形配置中。

按一定隊形配置的編隊防空作戰體系作為防御方，主要任務是在殺傷區內盡可能多地殺傷目標數，制止空襲目標突擊編隊或阻止目標通過編隊殺傷區，使編隊的安全系數或者生存概率最大。因此，編隊防空系統殺傷目標期望可以較全面地衡量編隊隊形配置的優劣。該期望值是抗擊連續空襲時，武器能攔截目標數量的最大值，由射擊次數和殺傷目標概率決定。當給定目標流和防空武器參數時，該武器的殺傷概率即可確定。因此，射擊次數即成為衡量防空火力配系優劣的一個核心指標。

本文依據這一特點，引入隊形配置決策向量，給定多方向來襲的目標流，以一字隊形為例，建立以總射擊次數為目標函數的隊形配置模型，旨在解決編隊抗擊多方向目標流的隊形優化配置問題。

1 編隊協同射擊次數模型

1.1 單艦射擊次數模型

當來襲目標航路捷徑為零時，理想狀態下，第1個彈目遭遇點恰好位于艦空導彈殺傷區遠界上，最后1個彈目遭遇點恰好位于殺傷區近界上，則艦空導彈攔截射擊次數為[5]

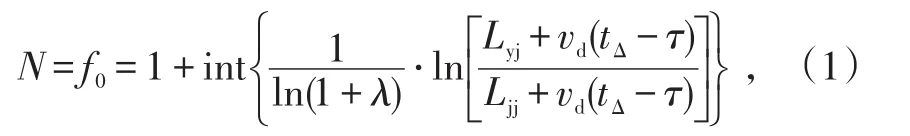
式中：Lyj、Ljj分別為艦空導彈武器系統殺傷區遠界和近界；vd為艦空導彈的平均飛行速度；tΔ為艦空導彈發射間隔時間與該枚防空導彈飛行時間的差值；λ為目標平均飛行速度與艦空導彈平均速度之比值。

在非零航路捷徑時，假定來襲目標以高度H、航路捷徑P運動，如圖1所示[6]。

圖1中，O點為艦空導彈發射點位置，目標的航路捷徑點記為CPA點。Ti點為第i枚防空導彈與目標遭遇時刻所在位置，i=0,1,…,N，N為艦空導彈武器系統的總射擊次數；Di為該時刻目標在水平面內的斜距；θj為在彈目遭遇點處的目標角；αj為艦空導彈的前置射擊角。依據圖1的幾何關系，當目標越過艦空導彈的殺傷區近界時，目標已突防，此時迎擊的射擊次數達到最大。則：

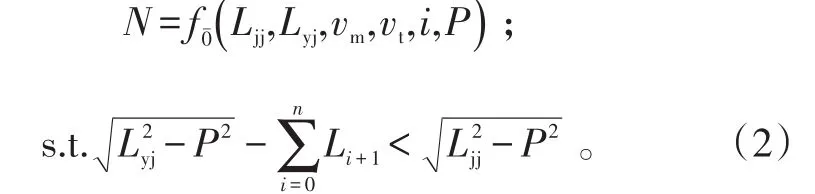
式（2）中[5]：

1.2 鄰艦的掩護射擊次數模型

假設來襲目標朝O1艦進攻，O2艦為掩護艦。圖2中扇形區域ABC所圍區域就是O2艦對O1艦的協同防空區域。在圖2中所示的協同射擊態勢圖中，目標相對O1、O2艦的航路捷徑分別為P1、P2，則兩艦的掩護射擊次數可等效為各自對殺傷區縱深為M1M2的目標在非0航路捷徑下進行射擊的次數。

Lyj為O2艦的殺傷區遠界，Qm為目標相對O1艦的舷角，Qmin為O1艦艦空導彈的最小射界，d為O1和O2兩艦間距，θ為O1相對O2舷角，也稱為看齊角。

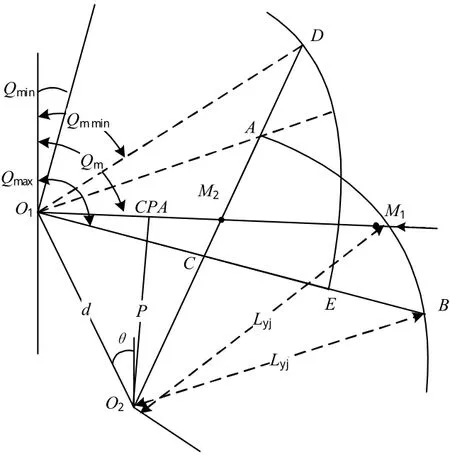
圖2 鄰艦掩護殺傷區Fig.2 Diagrammatic sketch of adjacent ship covering kill zone

在理想情況下，M1點恰好位于防空導彈的殺傷區遠界上，則協同射擊時的第一個彈目遭遇應該位于M1點處。當目標越過M2點時，目標實現突防。此時，掩護射擊次數達到最大，則掩護艦在非零航路捷徑下的射擊次數為[7]：

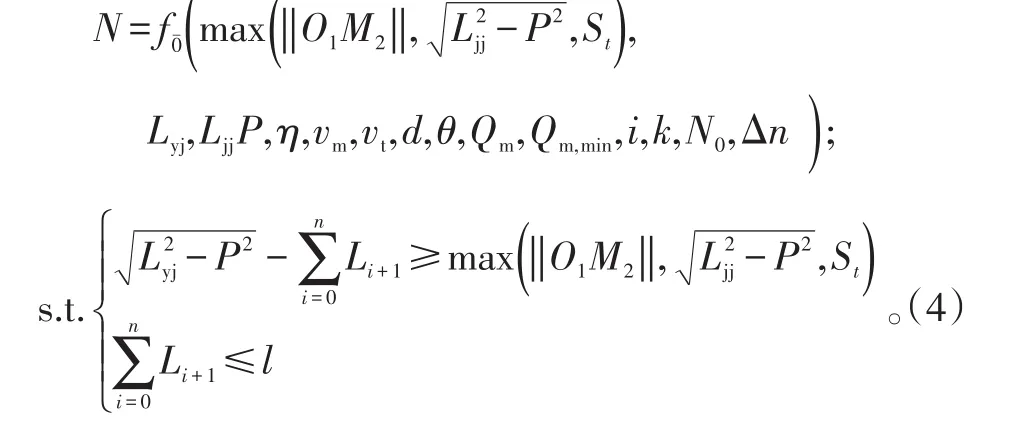
式（4）中，Li

1.3編隊總射擊次數模型

編隊總射擊次數是編隊內各協同成員的射擊次數之和。以雙艦編隊為例，來襲目標攻擊其中一艦時，另一艦即為掩護艦，此時，編隊總的射擊次數就由被攻擊艦對（零航路捷徑）目標的射擊次數與掩護艦對（非零航路捷徑）目標的射擊次數之和。當增加編隊成員數目和來襲目標流數目時，對每一批目標，同樣存在被攻擊艦和掩護艦的集合。則編隊總的射擊次數Ntotal存在如下關系：

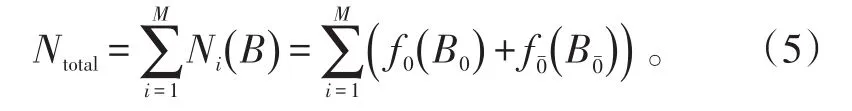
式（5）中：M為來襲目標流批數；Ni為編隊抗擊第i批目標的射擊次數；B為能夠抗擊第i批目標的艦艇集合；B0為被攻擊艦；B0ˉ為掩護艦集合，且滿足

式（6）表明：編隊抗擊多批次、多方向來襲目標流時，預計的總射擊次數是M個集合B的射擊次數之和。當給定威脅目標和艦空導彈武器參數時，因為被攻擊艦的抗擊次數保持不變，編隊總的射擊次數就與掩護艦的射擊次數相關。由1.2節分析可知，影響掩護艦射擊次數的關鍵參數為該防空武器的殺傷區縱深。因此，可以利用該參數與隊形配置向量、射擊次數之間的約束關系建立綜合配置模型。

2 編隊對多方向目標流射擊次數模型

編隊隊形是由編隊成員在空間內的相對位置即艦艇之間的距離d和看齊角θ唯一確定的。其中，艦艇間隔距離主要影響編隊的目標探測能力以及目標的防御縱深。看齊角則直接影響編隊整體防御區域的大小和對目標的攔截效果。調整和改變編隊隊形，實際上就是改變d和θ，將編隊火力單元進行合理配置，在重點部署區域將同型或異型的火力單元殺傷區進行耦合，能改善火力結構，提高集火能力。

雙艦編隊隊形的一般研究方法都是假設編隊防空導彈武器類型、性能一致，在給定威脅目標的情況下，協同殺傷區縱深最大對應的隊形配置就是最優配置。但是，由于多艦編隊的艦空導彈武器多種多樣，協同殺傷區縱深計算方法與雙艦編隊的計算方法有較大區別，因而該方法不能直接應用于多艦編隊的隊形配置。

為獲得多艦編隊的更具廣泛意義的驅護艦編隊隊形配置，設計優化方法思路為：給定威脅目標流，建立一字隊形防空態勢，引入隊形配置向量進行殺傷區縱深計算，以編隊所有艦艇對所有目標的總的射擊次數為目標函數，在受約束的決策空間內尋找使目標函數達到最大的向量，即為最優的編隊隊形配置方案。當編隊內艦空導彈武器系統不一致時，該Aˉ為一決策矩陣。

2.1 一字隊形防空態勢

現代艦艇編隊防空的來襲目標流以導彈流為主。給定四個方向上的導彈流，認為該導彈流臨空時間間隔的數學特性符合巴爾姆流[8]，且在不同的突擊樣式下會呈現出不同的分布。假設編隊序列為(J0,J1,J2,J3,J4)，其中J0為被掩護的指揮艦，其余四艘艦艇為掩護艦。導彈流均向J0攻擊，則忽略J0的防空能力，重點考察掩護艦的情況。J1、J2為護衛艦，裝備了相同型號的中近程艦空導彈武器系統，J3、J4為驅逐艦，裝備了相同型號的中遠程艦空導彈武器系統，導彈武器均具有全向攻擊能力。一字隊形下編隊抗擊導彈流的態勢圖如圖3所示。

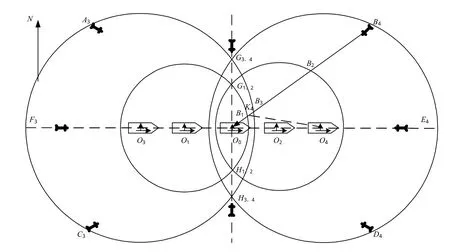
圖3 一字隊形編隊抗擊多方向目標流態勢圖Fig.3 Situation chart of fleet in line-type formation intercept multi-direction target flow

圖3中來襲目標流序列為Mi，i=1,2,…,8，該序列的航向角為βi。編隊隊列線與正北方向的夾角為α，α=π/2。編隊成員航向角保持一致。艦艇序列在過指揮艦質心的水平面內投影為：(O0,O1,O2,O3,O4)。集合(Ai,Bi,Ci,Di,Ei,Fi,Gi,Hi)為8批目標流航路與4艘掩護艦防空導彈殺傷區遠界的交點(i=1,2,3,4)。

因為圖3中坐標系的對稱性，以第I象限的目標序列M2為例進行分析。該目標序列相對J0的舷角Qm02=α-β2。以O0為原點，以指揮艦艏艉線的延長線在水平面內的投影為X軸，艦艏方向為正；艏艉線的垂線在水平面內的投影為Y軸，向右方向為正，建立坐標系。不妨設0≤α≤π/2，則當目標航向角，坐標軸XOY沿順時針方向旋轉π/2-α，得到指向正東和正北方向的坐標軸X′OY′。對圖3作簡化處理，如圖4所示。

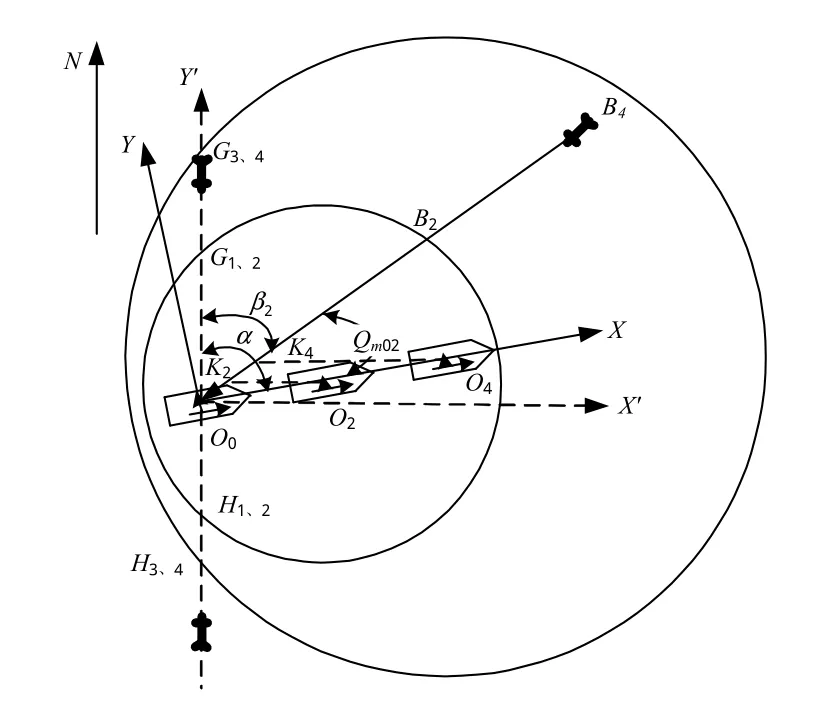
圖4 第I象限目標流的攻擊態勢圖Fig.4 Engagement situation chart of first quadrant

2.2 一字隊形優化配置模型

由圖4知：掩護艦J4對目標流M2的殺傷區縱深為為J4受J2影響的禁危區邊界，點K4為該目標流航路與的交點。利用三角關系，有：

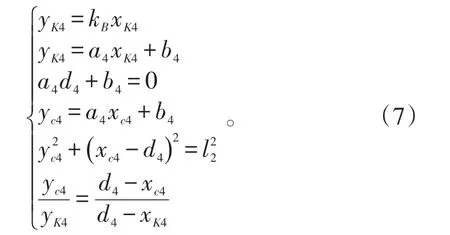
a4、b4為J4受該禁危區影響的射界直線參數為該射界線與禁危區的交點坐標。

同理，可得：

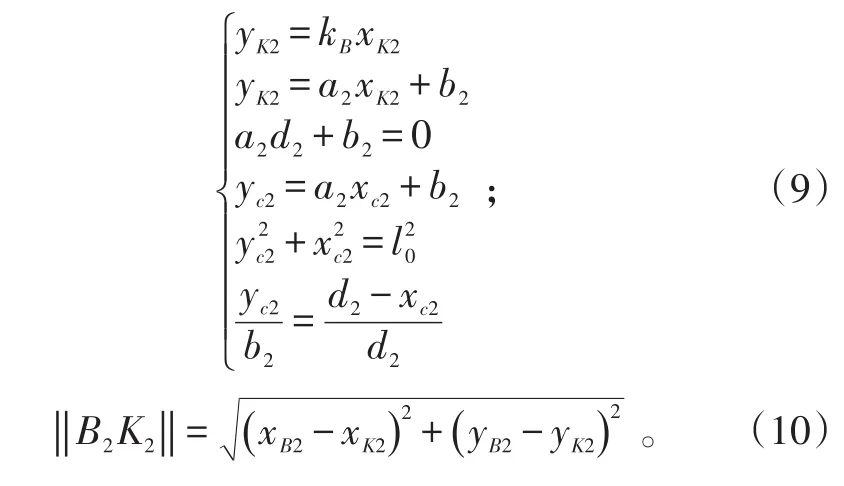
同理，可得到J1和J3對該目標流的殺傷區縱深計算式。雖然目標流航路B4O0與J1和J3的殺傷區遠界存在交點，但是由于該交點可能位于鄰艦影響的射擊禁危區內，導致不能對M1進行抗擊。因此，必須對該交點進行禁危區判斷，即：

式（11）中：xB1、xB3為J1、J3殺傷區遠界與目標流交點的橫坐標；xK1、xK3為目標流航路與J1、J3禁危區邊界交點的橫坐標。

成一字隊形時通常滿足：d1=d2，d3=d4。

令Qmij為目標i相對艦艇j的舷角。當編隊成一字隊形時，θ=0。可建立第一象限的編隊總射擊次數計算模型：

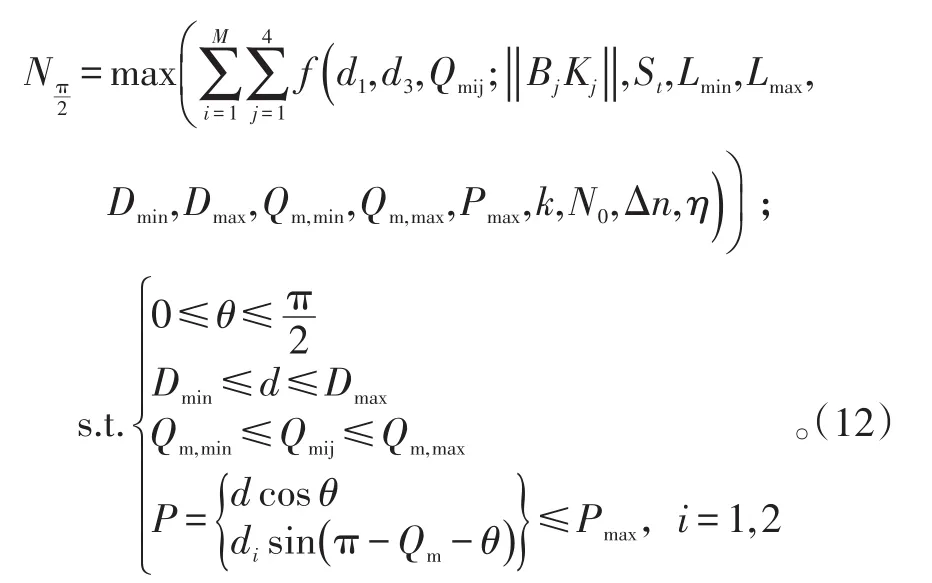
式（12）中，對被攻擊艦艇，采用式1的零航路捷徑射擊次數計算式；對掩護艦，采用式2~4的非零航路捷徑射擊次數計算式。

以上給出的是在給定防空武器系統配置的情況下，編隊對以一定方位角進入防空區域的單個目標序列的射擊次數計算方法。假設在圖4所示的90°范圍內，目標進入方位角服從分布密度函數為的某一分布，則在整個圖3所示的圓周區域內，編隊抗擊多方向目標流的總射擊次數期望為：

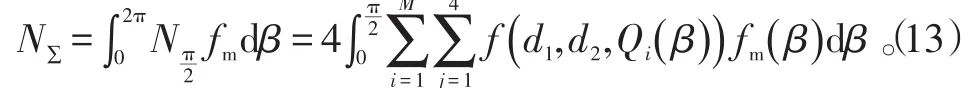
上式與式（12）具有相同的變量約束。

3 仿真分析

對圖4所示的攻擊態勢，依據文獻[9]，設來襲目標為反艦導彈，vt為330 m/s，飛行高度為30 m，β2為30°，α為60°，假設艦艇間距相等，即d=d2=d4-d2，J2、J4的艦空導彈飛行速度均為1 000 m/s，艦空導彈武器系統為單通道系統且具有全向攻擊能力[10]，殺傷區遠界分別為12km和15km。令艦艇間距d在0~ 120鏈范圍內變化，得到仿真結果如圖5所示。圖中，縱軸表示J2和J4艦對來襲目標的射擊次數之和，橫軸為d。艦艇間隔距離單位為鏈（Cab=10-1nmile）。由圖5知，當艦艇間距從0逐漸增大時，J2和J4對目標流的殺傷區縱深增大。但是，在（0,280）Cab內，兩艦對目標的抗擊可以近似為0航路捷徑的抗擊過程，所增加的縱深尚不足以使艦空導彈完成一次完整的射擊周期，因而總射擊次數保持不變。在（28,46）Cab內，間距對總射擊次數的影響較大，從8.2次增大到了13.3次。在間距d約為41 Cab處，J0艦恰好位于J4艦殺傷區遠界上，此時，J4艦對目標的射擊次數達到最大，繼續增大等間距d，則抗擊目標的縱深逐漸減小，導致射擊次數的逐漸降低。

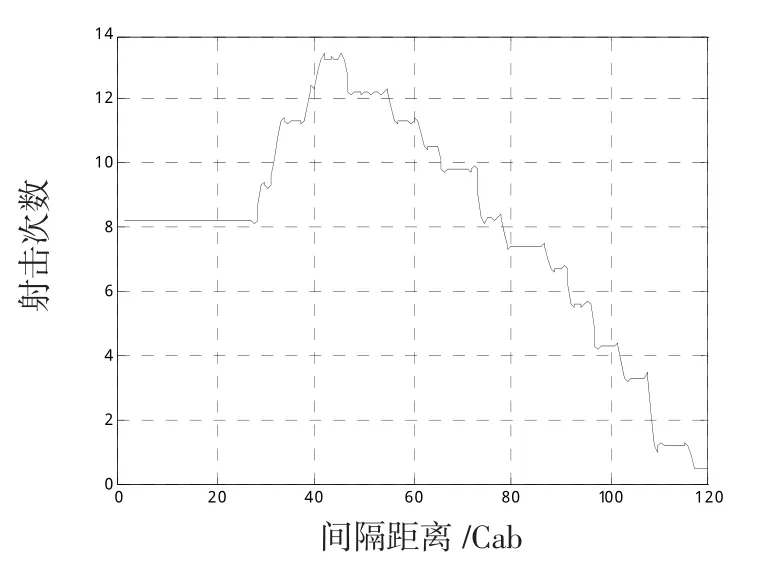
圖5 一字隊形下J2和J4的射擊次數Fig.5 Fire times ofJ2andJ4under line formation

圖4中，當d4≈82 Cab，d2=41 Cab時，由于J2的殺傷區遠界為12km，因而該艦對目標的殺傷區縱深依然具備增大的余地。此時，若保持J4艦的位置不動，繼續增大d2，則總射擊次數依將繼續增大。當d2=65 Cab，d4=82 Cab時，總射擊次數將達到14.8的最大值。

由于圖4是一個簡化態勢圖，僅表示了單個象限內的防空態勢，且圖5的仿真結果也只對目標流M2進行了仿真。實際在圖3中，在第I象限內有3個目標流，分別是M1、M2和M3。由于M3位于隊列線上，只能由J4艦單獨進行抗擊，因此，該象限實際能夠協同抗擊的目標流為M1和M2。M1位于J1和J2、J3和J4的耦合殺傷區內，該耦合殺傷區隨著艦艇間距增大而減小。由于J2和J4對2個目標流的攔截過程具有相同特性，因而以J2艦為例進行仿真，得到圖6。圖6中，橫軸為d2，縱軸為J2艦對2個目標流的射擊次數。

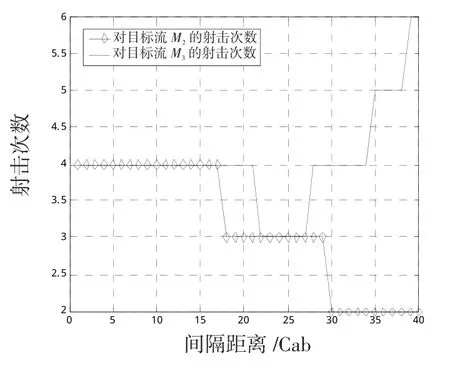
圖6 第I象限2個方向來襲目標流射擊次數與間距關系Fig.6 I llustration for fire frequency to ships intervals with two different direction targets flows in first quadrant

由圖6可知，當d2較小時，J2艦對2個目標流的殺傷區縱深均為12km，因而射擊次數也一致。d2逐漸增大，J2對M1的縱深逐漸減小，對M2的縱深B2O0分為二段，其中，B2O2隨著d2的增大逐漸減小，而O2O0則逐漸增大，在增大至L2min之前，艦空導彈都不能對該目標流進行射擊，因而J2的總射擊次數僅與B2O2相關，與O2O0無關。因此，在d2達到21 Cab時，射擊次數下降。此后d2繼續增大，O2O0的距離也越過J2的殺傷區近界，使射擊次數開始增加。當d2=42 Cab時，目標流相對J2艦空導彈的航路捷徑為7.7km，超出了該型導彈能夠攔截的最大航路捷徑P2max，因而對M1的射擊次數為0。

由以上討論可以看出，對圖4的防空態勢，雖然增大艦艇間隔距離能夠增加對隊列線方向來襲目標流的射擊次數，卻相應的減小了對垂直于隊列線方向來襲目標流的射擊次數，因而對來襲方向不同分布的目標流需要采取不同的間隔距離配置方式。

0,30 Cab，L2jj=3km，對J2按照隊形向量關系進行射擊次數仿真，結果如圖7所示。

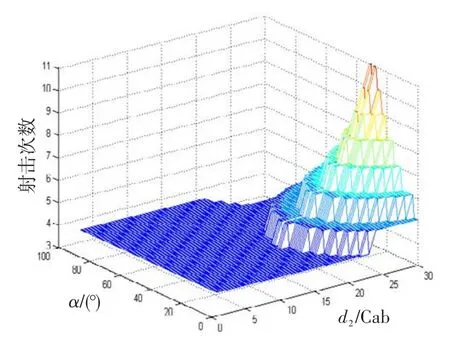
圖7 不同隊形配置下J2對M2的射擊次數Fig.7 Fire times ofJ2toM2under different formation

圖4中，給定目標流M2的航向角時，J2艦對目標流M2的射擊次數與隊列線的方位角相關。與只有迎擊殺傷區的雙艦協同情況不同，具有全向攻擊能力的一字隊形編隊，相對舷角Qm02越小，隊列線方位角越貼近目標流來襲方向，相應的射擊縱深越大，射擊次數也越大。當Qm02=0時，隊列線與目標來襲方向重合，位于J2后方的區域為射擊禁區，因而J2對目標流的射擊縱深為Lyj，此時，射擊次數下降到5次。

4 總結

海上編隊防空隊形配置是編隊火力運用的重要問題之一。本文利用射擊次數與殺傷區縱深、隊形配置向量之間的約束關系，建立了一字隊形優化配置模型，通過射擊次數來衡量隊形的優劣，并進行了仿真驗證。為艦艇編隊防空隊形優化提供了新思路。

由于篇幅所限，本文僅就一字隊形展開了建模仿真，下一步將把該優化配置模型的構建方法應用于其他典型防空隊形，如菱形、人字形等，并針對具有區域防空導彈武器和近程防空導彈武器相結合的艦艇編隊防空隊形問題進行具體研究[11-12]，以明確量化的指標實現幾種隊形的優劣評判，為編隊防空作戰指揮決策提供參考。

[1]李永剛.艦艇編隊對空防御隊形優化配置模[J].情報指揮控制系統與仿真技術，2000，26（4）：65-67. LI YONGGANG.A model of optimal disposition of warship formation for air defense[J].Information Command Control System&Simulation Technology，2000，26（4）：65-67.（in Chinese）

[2]譚安勝，邱延鵬，汪德虎.新型驅護艦編隊防空隊形配置[J].火力與指揮控制，2003，28（6）：5-9. TAN ANSHENG，QIU YANPENG，WANG DEHU.Investigation on air defense disposition for formation of destroyers and escort vessels[J].Fire Control&Command Control，2003，28（6）：5-9.（in Chinese）

[3]徐勝良，王振波.航母編隊航渡過程中防空哨戒艦陣位確定方法研究[J].指揮控制與仿真，2007，29（4）：54-58. XU SHENGLIANG，WANG ZHENBO.Research on the position of air defense-guard ship for carrier formation during navigation[J].Command Control Simulation，2007，29（4）：54-58.（in Chinese）

[4]趙建印，劉芳.海上編隊雙艦防空隊形部署優化研究[J].兵工學報，2010，31（6）：865-869. ZHAO JIANYIN，LIU FANG.Deployment optimization of two warships formation for air defense[J].Acta ArmamentarⅡ.2010，31（6）：865-869.（in Chinese）

[5]丹尼爾·瓦格納，查爾斯·米蘭德.海軍運籌分析[M].姜青山，鄭保華，譯.北京：國防工業出版社，2009：286-298. DANIEL H WAGNER，W CHARLES MYLANDER.Naval operation analysis[M].Traslated by JIANG QINGSHAN，ZHEN BAOHUA.Beijing：National Defense Industry Press，2009：286-298.（in Chinese）

[6]譚安勝.水面艦艇編隊作戰運籌分析[M].北京：國防工業出版社，2009：221-240.（in Chinese）TAN ANSHENG.Surface fleet operation analysis[M]. Beijing：National Defense Industry Press，2009：221-240.（in Chinese）

[7]范英飚，姚躍亭，高波.艦艇編隊協同防空連續射擊次數仿真分析[J].計算機工程與設計，2011，32（6）：2092-2095. FAN YINGBIAO，YAO YUETING，GAO BO.Analysis and simulation on continuous fire frequency of coordinate air defense in warship formation[J].Computer Engineering and Design，2011，32（6）：2092-2095.（in Chinese）

[8]高山，李孝軍，陳杰生.面向防空的空襲目標流時間特性分析[J].空軍工程大學學報：自然科學版，2008，9（1）：41-45. GAO SHAN，LI XIAOJUN，CHEN JIESHENG.The analysis of time characteristic of air-raid target stream for air defense[J].Journal of Air Force Engineering University：Natural Science Edition，2008，9（1）：41-45.（in Chinese）

[9]高雁翎，施榮，黃莉茹，等.世界防空反導導彈手冊[K].北京：國防工業出版社，2010：410-413. GAO YANLIN，SHI RONG，HUANG LIRU，et al.Manual of antimissile missile in the world[K].Beijing：National Defense Industry Press，2010：410-413.（in Chinese）

[10]沈治河，杜一平.關于水面艦艇編隊防空隊形的研究[J].海軍大連艦艇學院學報，1996，19（3）：17-19. SHEN ZHIHE，DU YIPING.Study on surface fleet antiair formation[J].Journal of Dalian NavalAcademy，1996，19（3）：17-19.（in Chinese）

[11]馬雷挺，熊吉光.有區域防空導彈的驅護艦編隊防空隊形研究[J].海軍大連艦艇學院學報，2000，23（4）：10-12. MA LEITING，XIONG JIGUANG.Study on anti-air formation of surface fleet with area air defense missile[J]. Journal of Dalian Naval Academy，2000，23（4）：10-12.（in Chinese）

[12]馬其東，方立恭.海上區域防空目標威脅評估模型[J].現代防御技術，2009，37（1）：15-19. MA QIDONG，FANGN LIGONG.Research on threat assessment model of air target for area air defense[J].Modern Defence Technology，2009，37（1）：15-19.（in Chinese）

Optimal Allocation of Anti-Air Warships Formation Based on Fire Times

WENG Lu1,YAO Yue-ting2,LIU Jian-feng1,MENG Fan-lei2
（1.Naval Equipment Department,Beijing 100841,China; 2.Department of Airborne Vehicle Engineering,NAAU,Yantai Shandong 264001,China）

An optimal method using firing times to the target flow as objective function was brought forward.The objective function was divided into two parts,one with zero course shortcut and another with none zero course shortcut.And the calculate method was given with the bounded relation between firing times,kill zone depth and formation deployment vector. Taking the trail formation as an example,the optimal model was constructed.

anti-air warships formation optimal allocation;fire times;multi-direction targets flow;trail formation

E928.674

A

1673-1522（2014）01-0087-06

10.7682/j.issn.1673-1522.2014.01.019

2013-10-20；

2013-12-10

翁璐（1979-），男，碩士。

Key words: