通用幾何約束系統統一建模研究

石志良，陳誼，張忠全

武漢理工大學機電工程學院，武漢 430070

通用幾何約束系統統一建模研究

石志良，陳誼，張忠全

武漢理工大學機電工程學院，武漢 430070

在幾何約束和幾何實體的基本約束和歐拉參數表達的基礎上，研究了通用幾何約束系統的統一建模問題。通過對三維幾何實體姿態約束和位置約束解耦性的分析，抽象出球實體、盒體和球盒體三種基本幾何實體表達空間幾何實體，并以基本約束的組合表達幾何約束，形成幾何約束模型特有的層次結構；并以有向圖管理幾何約束系統，可以清晰地反映姿態約束和位置約束的解耦性，實現約束系統的細粒度分解，得到規模更小的求解序列，實現高效求解。方法實現于原型系統WhutVAS中。

幾何約束；幾何約束求解；約束處理；圖分解；歐拉參數

1 引言

在幾何約束系統中，幾何實體之間的約束關系是非常復雜的，如何建立有效的幾何約束系統模型，是幾何約束系統研究的基礎。理想的幾何約束系統應該做到表達、維護和求解的一致性，幾何空間的可拓展性及幾何上的可解釋性。在幾何約束系統的研究中，基于變量幾何[1-3]的幾何約束系統建模方法，以幾何實體特征點的參數變量來表達幾何實體，以參數變量之間的約束方程來表達幾何約束，其局限性是顯而易見的。這種采用整體笛卡爾坐標建立系統約束和約束方程的方法雖然從理論上來說可以進行任何類型的約束求解，但它需要建立一個較大的方程組，對于幾何約束的表達和求解都很不方便。基于幾何實體和圖論[4-9]對幾何約束系統進行建模，可以直接管理二、三維空間中的幾何實體及其關聯的幾何約束，具備較好的幾何空間可拓展性及幾何上的可解釋性，但是，由于幾何約束的多樣性，導致幾何約束的表達復雜，簡潔性不夠，而且裝配約束的約束度通常大于1，不利于冗余約束的判定。為了解決這些問題，需要研究基礎共性的表達問題，彭小波[10]以運動學和動力學的研究為基礎，提出采用歐拉參數和基本約束[11]表達幾何實體和幾何約束，結合有向圖，在幾何建模的層次上將二、三維幾何約束問題以及多剛體系統動力學問題統一起來，并擴展到多剛體系統的分析計算領域，該方法以少量的基本幾何約束表達所有的幾何約束，模型的抽象和簡潔性好，然而，卻忽視了歐拉參數表達的幾何實體參數結構上具有一定的可解耦性，對幾何實體的統一表達沒有作進一步的研究和抽象，有向圖頂點仍然是通常的幾何實體，從而導致求解的規模較大。文獻[12]研究了三維實體之間的重合、角度和距離約束的統一幾何表達。本文以歐拉參數表達的幾何實體的姿態和位置約束的解耦性研究為基礎，抽象出球實體、盒體和球盒體三種基本幾何實體表達空間幾何實體，并采用基本約束的組合表達幾何約束，在有向圖上清晰地表達幾何約束系統的本質特征，基于有向圖的幾何約束優化匹配算法[13]，為二、三維幾何約束求解提供了內在的統一機理，具有很強的理論意義。

2 基于歐拉參數的幾何實體和幾何約束的表達

幾何實體的方位由姿態和位置確定，姿態表示幾何實體在空間中的方向，如平面的法向量，直線的方向，剛性體的方向余弦矩陣，可以由附著在幾何實體上的局部坐標系的姿態表達；位置由附著在幾何實體上的局部坐標系的位置表達，Haug[11]采用歐拉參數表達幾何實體的方位，以基本約束dot1、dot2、等X、等Y、等Z和距離條件[10]表達裝配約束。由于三維空間復雜于二維空間，二維空間的歐拉參數表達可以看作是三維空間的特例，因而，本文僅給出三維常見裝配約束的基本約束表達，如表1所示。

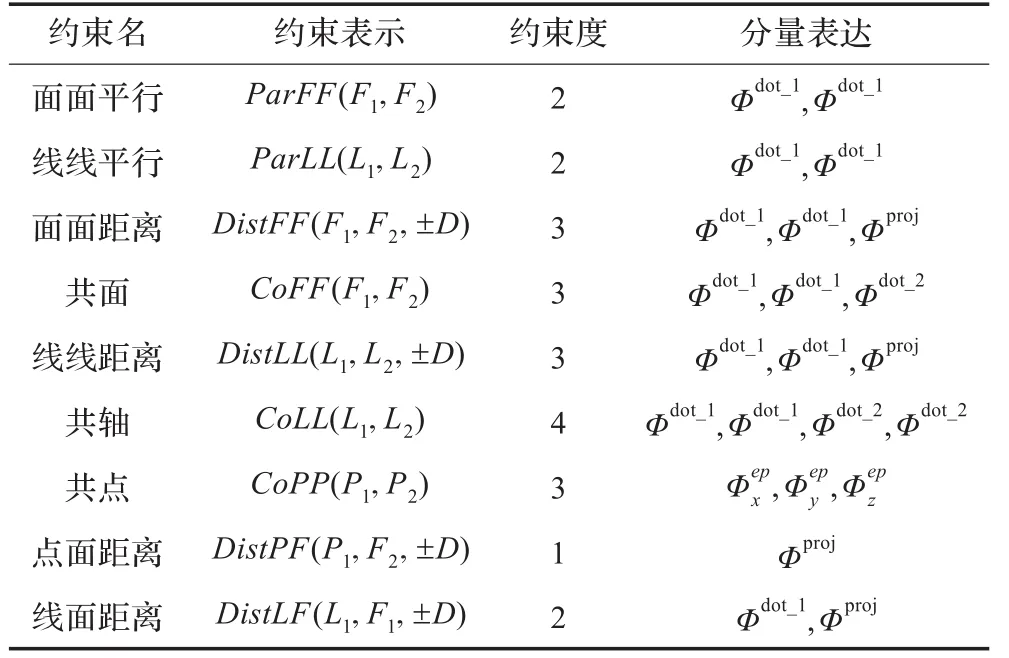
表1 常用裝配約束及其位置基本約束表達1）

以共軸約束為例，共軸約束限制4個自由度，如圖1 （a）所示，假定P1和P2分別是軸線L1和L2的基點，h1，h2分別是軸線L1，L2的方向矢量，矢量f1，g1，h1正交，假定軸線L1固定，要使L1和L2共軸，需要滿足f1⊥h2，g1⊥h2，f1⊥d12和g1⊥d12，f1⊥h2和g1⊥h2決定圓柱體2的姿態，f1⊥d12和g1⊥d12決定圓柱體2的位置，對應的約束方程如圖1（b）。

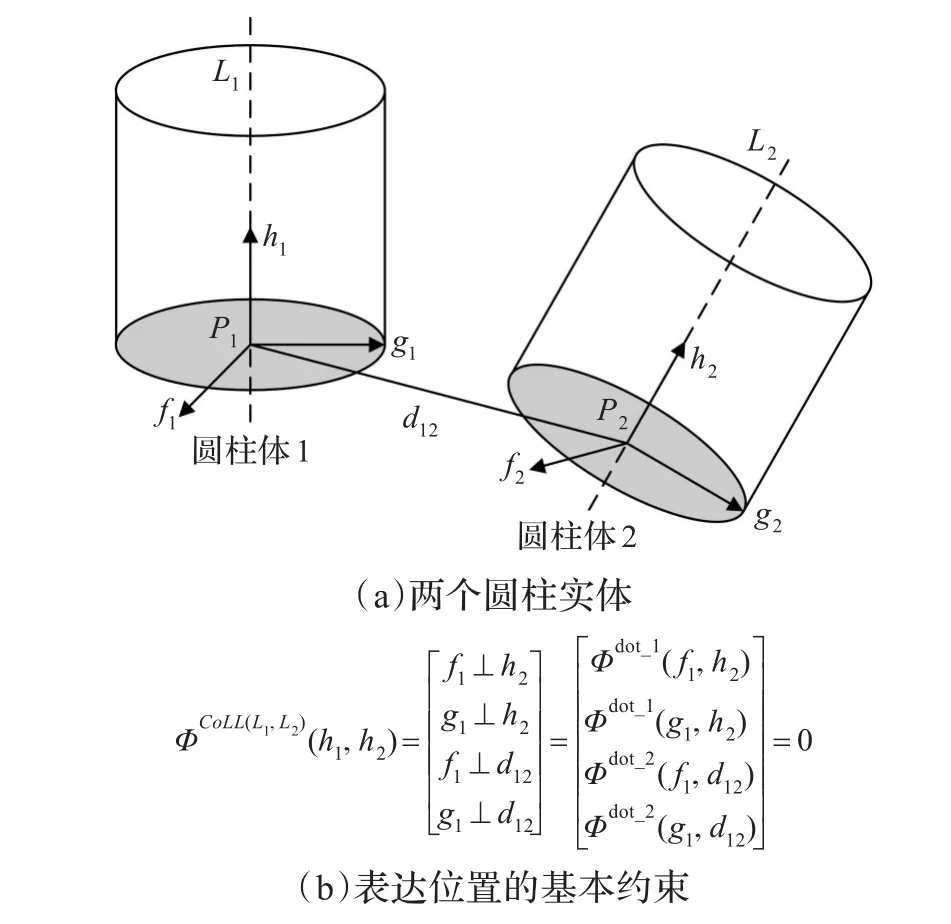
圖1 圓柱體共軸約束實例圖

3 幾何實體姿態和位置的解耦性質

幾何實體的姿態和位置具有一定的可解耦性質，有利于求解。因為從幾何上來說，存在這樣一個事實：移動幾何實體不破壞幾何實體的姿態，而轉動幾何實體時卻可以破壞幾何實體的位置例如，共軸約束含有4個約束分量，約束度是4，在可解耦的情況下，共軸約束的4個約束分量可以分為軸平行的2個姿態約束和點在軸線上的2個位置約束，求解時可以先根據姿態約束確定姿態，然后在確定的姿態下，求解位置約束，反之則不能夠求解。當然，也可以采用整體數值求解，需要聯立4個方程，效率顯然較低。假設以代表基本約束dot1，代表基本約束dot2是指其他的距離約束關系，存在如下性質：

性質1假設剛性體RB參數匹配的約束滿足條件

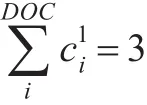
姿態約束和位置約束是可以解耦求解的。剛性體存在三個約束，表明姿態是完整約束的，則不論剛性體是完整約束還是欠約束，一定是可解耦求解的，如3A 3D、3A 2D和3A 1D構型[13]。

性質2如果與剛性體RB參數匹配的和約束滿足條件

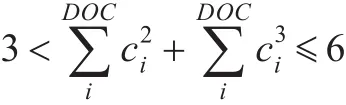
則姿態約束和位置約束一定不可解耦求解。

由于剛性體存在三個移動自由度，如果匹配的和約束數大于3，那么需要通過轉動來滿足約束，使得姿態和位置約束求解不可解耦。如2A 4D、1A 5D和6D完整約束構型[14]。

如果在可裝配的條件下，排除性質1和性質2的情況，處于欠約束情況下的姿態和位置的解耦求解不存在定性，常見的裝配約束都是可以解耦的，例如兩個剛性體上兩個軸線的共軸約束、平行軸相距約束、兩個平面的共面約束、面面相距約束等，姿態和位置是可以解耦求解。但是，如果兩個剛性體受到一個平行約束和兩個距離約束，剛性體初始方位的不同，可能會導致不可解耦求解，需要同時變換剛性體的姿態和位置來滿足距離約束。雖然欠約束情況下的姿態和位置的解耦求解不存在定性，但是能夠分離出的可解耦情況對幾何約束求解是很有意義的。對于欠約束情況下的姿態和位置非定性解耦求解，通常是先求解姿態約束，然后依據位置約束和確定的姿態，判定是否存在解，如果存在，則可解耦，否則不可解耦，采用整體數值求解。

4 幾何實體的統一表達

4.1 基本幾何實體認定

由幾何實體的姿態和位置的解耦性分析，以及姿態約束和位置約束的性質可知，僅匹配幾何實體的姿態，和約束可匹配幾何實體的姿態和位置，由此可以產生一個很樸素的思想：

幾何實體所受的幾何約束中，讓決定幾何實體姿態的基本約束單獨求解幾何實體的姿態，而決定幾何實體位置的基本約束單獨求解幾何實體的位置，從而將幾何實體方位的統一求解分為姿態和位置的獨立求解，降低求解的規模。

為了在幾何約束圖上表達這種關系，需要對幾何實體的表達作進一步的研究和抽象，為此，引入球實體、盒體和球盒體三種基本幾何實體。球實體是一個只與空間方向相關的抽象實體，由歐拉參數組p=[e0，e1，e2，e3]表達，球實體僅與幾何實體的姿態相關，自由度是3；盒體是一個只與空間位置相關的抽象實體，由參數組r=[x，y，z]表達，盒體僅與幾何實體的位置相關，自由度是3；球實體和盒體可以表示幾何實體的方位，但是，三維空間的球面和圓柱面都存在一個形狀自由度，為清晰地表達球面和圓柱面，引入球盒體的概念，球盒體是一個與幾何實體的位置和形狀參數相關的抽象實體，由參數組r=[x，y，z]和形狀參數表達，自由度是4，表2是三種基本幾何實體的描述。

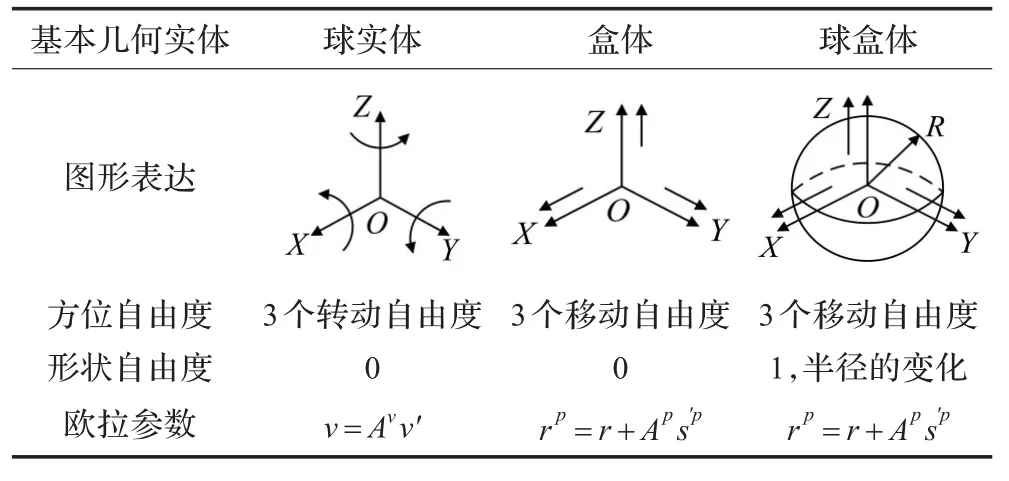
表2 三種基本幾何實體的描述

4.2 基于基本幾何實體的三維幾何實體表達

基于基本幾何實體，考察三維空間中的點、直線、平面、球面、圓柱面和剛性體，存在如下的表達方式：

（1）點

空間點的邊界表示為p(x，y，z)，歐拉參數表示為rp=r+Aps′p，自由度是3，因而以盒體表達。

（2）直線

在三維空間中，設固結在直線上的局部坐標系為o′x′y′z′，直線的位置由局部坐標系原點o′確定，歐拉參數表示為ro=r′+Aos′o；直線的空間姿態由x′y′z′的姿態確定，直線的方向由向量v′表示，歐拉參數表示為v=Avv′，與方向向量正交的向量為h和g，v′、h和g表示局部坐標系o′x′y′z′的姿態，由此可知，直線的姿態可以表示為球實體，直線的位置可以表示為盒體。在三維空間中，直線的自由度是4，球實體和盒體的自由度之和是6，則需要在球實體和盒體之間添加內部約束，以保證直線表達的正確性。取直線上的任意一點rp（不同于原點o′，該點相當于待確定直線上的點），則有rp和o′連線的方向與v′一致的條件成立，由基本約束可知，需添加2個dot2約束

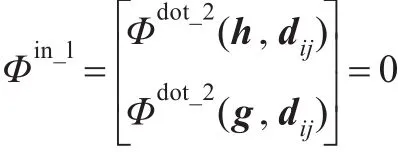
其中dij=rp-ro約束度是2，與三維空間直線的幾何意義吻合。

（3）平面

在三維空間中，設固結在平面上的局部坐標系為o′x′y′z′，平面的位置由局部坐標系原點o′確定，歐拉參數表示為ro=r′+Aos′o；平面的空間姿態由x′y′z′的姿態確定，平面的法向由向量v′表示，歐拉參數表示為v=Avv′，與法向量正交的向量為h和g，v′、h和g表示局部坐標系o′x′y′z′的姿態，由此可知，平面的姿態可以表示為球實體，平面的位置可以表示為盒體。在三維空間中，平面的自由度是3，球實體和盒體的自由度之和是6，則需要在球實體和盒體之間添加三個內部約束，以保證平面表達的正確性。取全局坐標原點到平面上的垂足為R，則有R和o′連線的矢量與v′滿足垂直約束，由基本約束可知，需添加1個dot2和2個dot1約束：

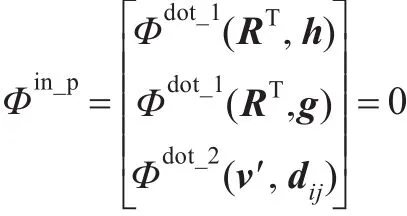
其中dij=R-ro。

（4）球面

在三維空間中，球面的位置由球心的坐標p(x，y，z)確定，由于球面具有空間對稱的性質，不具備方向，球面的半徑是形狀自由度，具有4個自由度，這些性質決定球面可以采用球盒體表達，球面的位置由歐拉參數表示為rp=r+Apsp。

（5）圓柱面

在三維空間中，圓柱面具有4個方位自由度和1個形狀自由度，方位自由度由圓柱面的軸線決定，形狀自由度表示圓柱面的半徑，根據直線的表達可知，圓柱面可以采用球實體和球盒體表達，同樣需要對球實體和球盒體添加兩個內部dot2約束，約束度為2。

（6）剛性體

三維空間剛性體的自由度是6，3個轉動自由度和3個移動自由度，由歐拉參數表達的3個轉動自由度由球實體表達，3個移動自由度由球盒體表達，球實體和球盒體之間不存在內部的約束關系。

通過對基本幾何約束和基本幾何實體的研究可知，裝配約束可以由基本約束的組合來表達，幾何實體可以由基本幾何實體和基本幾何約束的組合表達，這使得幾何約束模型的表達呈現出其特有的層次結構，如圖2所示。

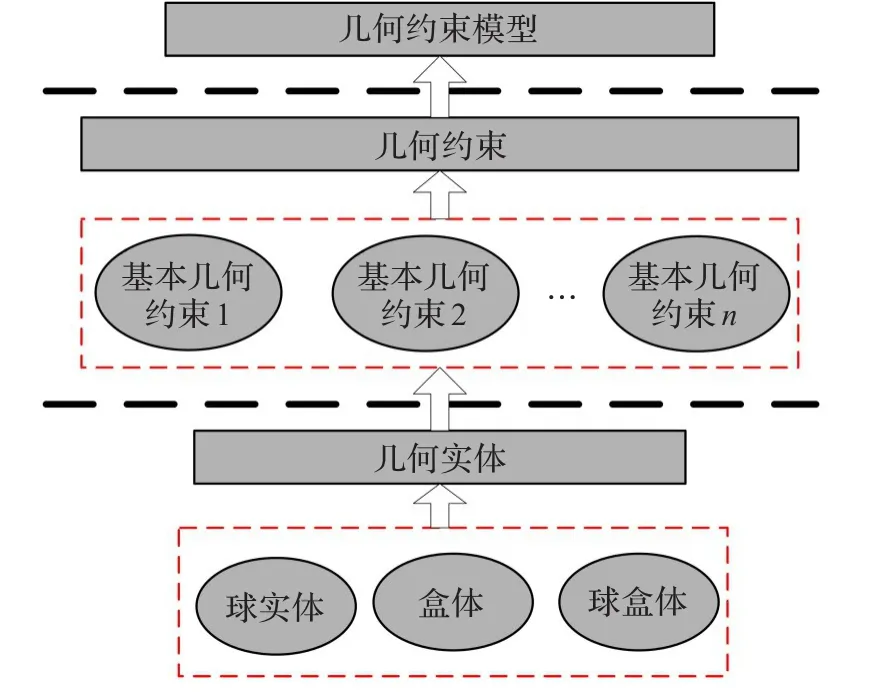
圖2 幾何約束模型層次結構圖

5 幾何約束系統建模

基于幾何約束模型層次結構，采用有向圖G=(V，A)描述幾何約束系統，其中V是表達幾何約束系統中所有幾何實體的頂點集合，以基本幾何實體表達幾何實體，則V僅由球實體、盒體和球盒體組成的集合。有向弧集合A={a}，一條有向弧表示一個基本約束，具有1個約束度，如果以有向弧直接表示裝配約束，而裝配約束的約束度通常大于1，則有向弧的權值大于1，導致在有向圖上無法清晰地表示冗余約束。

如果與頂點v匹配的約束數m小于其自由度DOF(v)，則稱頂點v是自由頂點；如果m等于DOF(v)，則稱v是固定頂點。在有向圖中，如果頂點v1到v2存在一條路徑P，且v1是自由頂點，則稱P是從v2到v1的逆向可逆路徑，簡稱可逆路徑。路徑P所包含的有向弧的條數稱為P的長度。如果G為有向無環圖，則從頂點v∈V出發的所有路徑上的頂點集稱為v的傳播域，從v出發所有逆向路徑上的頂點集稱為v的先決域。

構造幾何約束有向圖G的算法關鍵在于：在有向圖上為新增約束c尋找匹配頂點v，其實質是有向圖上的＜c，v＞二部圖匹配。簡單地說，構造幾何約束有向圖的過程實際上就是為每條有向弧確定匹配頂點的過程。

構造規則1如果兩個相關頂點中有一個頂點為固定頂點，另外一個為自由頂點，則約束與自由頂點匹配。

構造規則2如果不屬于同一個強連通分量的兩個相關頂點的均為自由頂點，則約束匹配于傳播域體積較小的頂點。

構造規則3如果兩個相關頂點的剩余自由度都為0，則從兩個相關頂點開始，找出一條最短的可逆路徑，將這條路徑反向，相應頂點的剩余自由度增加，新增約束與之匹配。

以上的三個構造規則是幾何約束與頂點匹配的通用規則，在以基本幾何實體表達的有向圖中，頂點僅由三種基本幾何實體組成，添加的裝配約束由dot1、dot2和距離等基本幾何約束組成，由于基本幾何約束的特定的性質，與基本幾何實體的匹配具有特殊的特性。

性質3dot1基本幾何約束只能夠在球實體之間依據構造規則匹配，如果不滿足匹配的條件，則該約束冗余。

性質4dot2基本幾何約束可以在球實體、盒體和球盒體之間依據構造規則進行匹配；如果待匹配的盒體或球盒體的剩余自由度為0，而該盒體或球盒體對應的球實體是自由頂點，dot2可與球實體匹配，否則，依據構造規則進行匹配。

性質5距離約束在盒體或球盒體之間依據構造規則進行匹配，如果待匹配的盒體或球盒體的剩余自由度為0，而該盒體或球盒體對應的球實體是自由頂點，距離可與球實體匹配，否則，依據構造規則進行匹配。

欠約束情形下的匹配多樣性會產生不良的強連通分量，增加求解時間花費。為此采用優化處理方法，文獻[13]對此作了詳細的闡述，最終得到一個強連通分量體積較優的求解序列。在求解序列中，對于每個幾何實體對應的基本幾何實體，如果是可解藕的，則先求解姿態和位置約束，然后求解內部約束。

6 實例分析

為驗證本文方法的正確性，采用一個回轉窯托輪軸裝配的實例進行驗證。圖3（a）為托輪軸裝配模型，其中裝配部件有中心軸1、托輪2、內擋圈3、軸承4、套筒5、軸承6和外擋圈7，爆炸圖如圖3（b）所示；裝配約束有共軸約束CoLL(1，2)、CoLL(1，3)、CoLL(1，4)、CoLL(1，5)、CoLL(5，6) 和CoLL(6，7)，共面約束有CoFF(1，2)、CoFF(1，3)，CoFF(3，4)、CoFF(4，5)、CoFF(5，6)和CoFF(6，7)。由于裝配部件為空間剛體，采用球體Si和盒體Bi分別表示部件i的姿態參數和位置參數，以分別表示部件i的轉動和移動，球體Si和盒體Bi分別具有3個轉動自由度和3個移動自由度。假設中心軸1的位姿固定，采用基本約束分量表達裝配約束，在剔除冗余約束分量后，可得到如圖3（c）所示的約束有向圖。該約束有向圖可采用并行求解，其求解序列如圖3（d）所示為{Sq0，Sq1，Sq2，Sq3，Sq4，Sq5，Sq6，Sq7，Sq8，Sq9}，其中Sq1和Sq5內的頂點可并行求解。

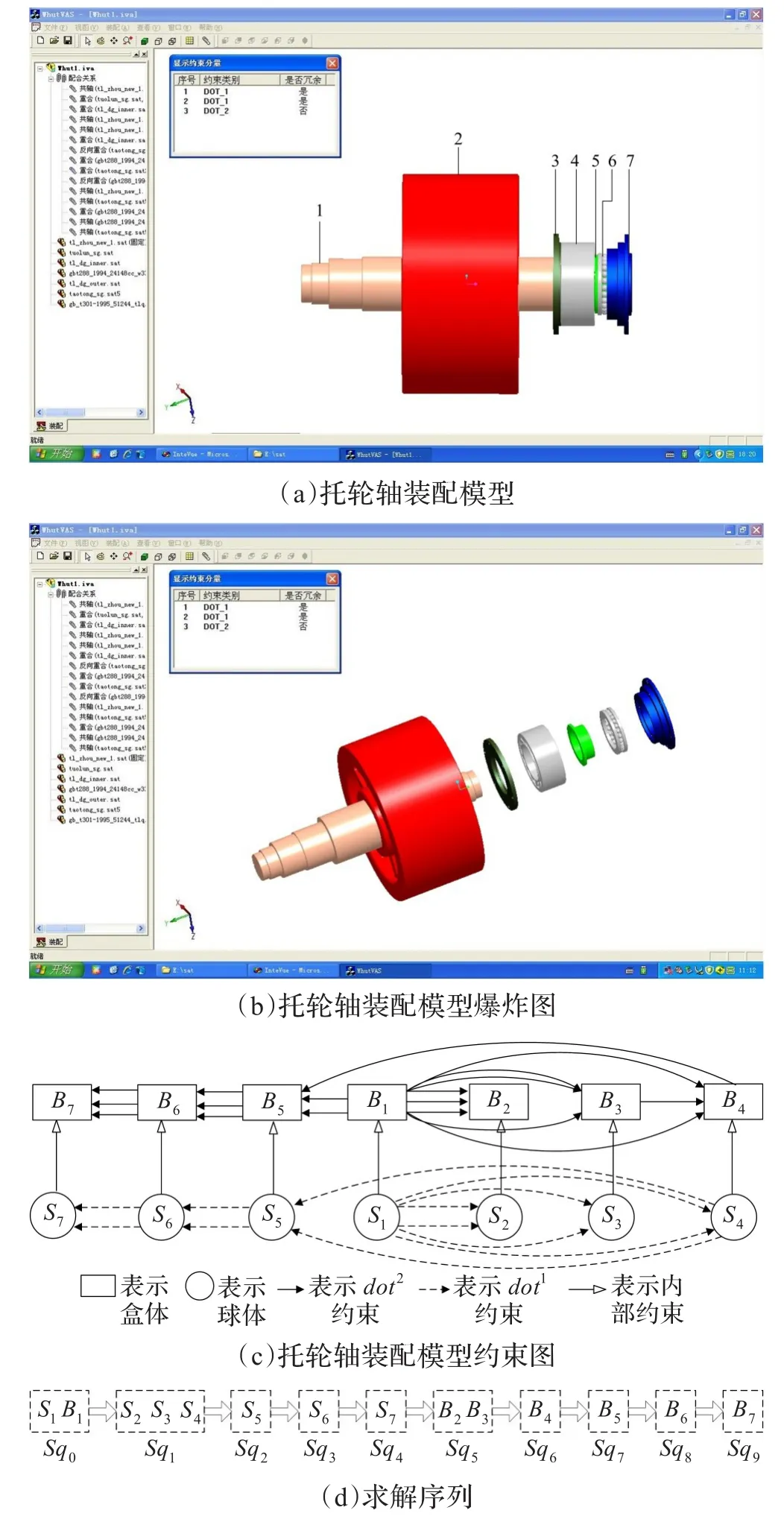
圖3 托輪軸裝配模型及其約束圖

7 結論

本文借鑒多體系統分析中的歐拉參數方法，以幾何實體和幾何約束的歐拉參數表達為基礎，通過對歐拉參數表達姿態約束和位置約束的解耦性分析，抽象出球實體、盒體和球盒體三種三維空間的基本幾何實體，并以球實體、盒體和球盒體對三維空間中的點、直線、平面、球面、圓柱面和剛性體進行統一表達，以簡潔的基本幾何實體和基本幾何約束，結合有向圖對幾何約束系統進行建模，描述了幾何約束求解的本質特征，可以清晰地表達姿態約束和位置約束的解耦性；本文的方法解決了二維與三維的幾何實體和幾何約束統一模型問題，為二、三維幾何約束求解提供了內在的統一機理，具有很強的理論意義，同時，為后續對姿態約束和位置約束分別采用解析求解，進一步提高求解效率奠定了基礎。但本文的表達模型適用于三維空間中的點、直線、平面、球面、圓柱面和剛性體之間的裝配關系，是否適用于除圓柱和球以外的二次曲面的表達需要做進一步的研究和完善。

[1]Lin V C，Gossard D C，Light R A.Variational geometry in computer-aided design[J].Compute Graphics，1981，15（3）：171-177.

[2]Serrano D，Gossard D.Constraint management in conceptual design[J].A rtificial Intelligence in Engineering Design，Computational Mechanics Publications，1988.

[3]A it-Aoudia S，Jegou R，Michelucci D.Reduction of constraint systems[C]//Combined Proceedings of EDUGRAPHICS’93 and COMPUGRAPHICS’93，1993：31-40.

[4]Owen J C.Algebraic solution for geometry from dimensional constraints[C]//Proceedings of ACM Symposium on Solid Modeling Foundation，Austin，TX，1991：397-407.

[5]K ramer G.Solving geometric constraints systems：a case study in kinematics[M].Cambridge，MA：M IT Press，1992.

[6]Hoffmann C M，Lomonosov A，Sitharam M.Decomposition plans for geometric constraint systems II new algorithms[J]. Journal of Symbolic Computation，2001，31（4）：408-428.

[7]Gao X S，Lin Q，Zhang G.A C-tree decomposition algorithm for 2D and 3D geometric constraint solving[J].Computer-Aided Design，2006，38（1）：1-13.

[8]董金祥，葛建新，高屹，等.變參繪圖系統中約束求解的新思路[J].計算機輔助設計與圖形學學報，1997，9（6）：513-519.

[9]李彥濤，胡事民，孫家廣.一個幾何約束系統分解的新算法[J].計算機輔助設計與圖形學學報，2000，12（12）：926-930.

[10]彭小波.二、三維幾何約束統一求解器原理與方法研究[D].武漢：華中科技大學，2002.

[11]Haug E J.機械系統的計算機輔助運動學和動力學[M].劉興祥，譯.北京：高等教育出版社，1996.

[12]Haller K，John A L，Sitharam M，et al.Body-and-cad geometric constraint system s[J].Computational Geometry：Theory and Applications，2012，45（8）：385-405.

[14]Gao X S，Lei D L，Liao Q Z，et al.Generalized Stewart-Gough platforms and their direct kinematics[J].IEEE Trans on Robotics，2005，21（2）：141-151.

[13]陳立平，王波興，彭小波.一種面向欠約束幾何系統求解的二部圖匹配優化處理方法[J].計算機學報，2000，23（5）：523-530.

SHI Zhiliang,CHEN Yi,ZHANG Zhongquan

School of M echanical and Electronic Engineering,Wuhan University of Technology,Wuhan 430070,China

A united modeling method of generalized geometric constraint system is investigated on the basis of expressing geometric constraints and geometric elements by basic geometric constraints and Euler parameter,respectively.After analyzing the decoupled property of orientation and position constraints related with spatial geometric elements,the basic bodies are summarized into ball,box and ball-box body to express spatial geometric elements,together with assembly constraints expressed by a combination of basic constraints,which forms a particular hierarchy structure of geometric constraint model.The geometric constraint system is coded as a directed geometric constraint graph which describes the relation among the basic geometric elements.The model method can reflect the decoupled property of orientation and position constraints clearly.The smaller solving units and the efficient solving sequence can be obtained.This method has been implemented in prototype system WhutVAS.

geometric constraint;geometric constraint solving;constraint handling;graph decomposition;Euler parameter

A

TP391

10.3778/j.issn.1002-8331.1209-0191

SH I Zhiliang,CHEN Yi,ZHANG Zhongquan.Research on united modeling method of generalized geometric constraint system.Computer Engineering and Applications,2014,50（16）：159-163.

國家自然科學基金（No.50905132）。

石志良（1974—），男，博士，副教授，主要研究方向為約束求解、參數化設計及智能CAD系統；陳誼（1988—），男，碩士研究生，主要研究方向為數字化設計。E-mail：shizhil998@yahoo.com.cn

2012-09-19

2013-01-05

1002-8331（2014）16-0159-05

CNKI網絡優先出版：2013-01-18,http://www.cnki.net/kcms/detail/11.2127.TP.20130118.1024.010.htm l