一種平移旋轉圖像的角點匹配方法

王小鵬，房超，雷濤

蘭州交通大學電子與信息工程學院，蘭州 730070

一種平移旋轉圖像的角點匹配方法

王小鵬，房超，雷濤

蘭州交通大學電子與信息工程學院，蘭州 730070

在圖像角點匹配過程中，目標圖像往往存在平移旋轉現象，直接影響匹配效果，為此提出了一種平移旋轉圖像的角點匹配方法。該方法首先利用角點檢測生成自相關矩陣的梯度信息與仿射變換相結合，構造確定性退火算法中的自由能函數，然后對該自由能函數進行優化，獲取待匹配角點間的仿射變換參數，最后利用該變換參數實現角點匹配。實驗結果表明，該方法能夠在目標圖像發生平移旋轉的情況下，有效實現角點匹配。

角點匹配；平移旋轉；確定性退火；仿射變換

1 引言

角點匹配指利用同一場景中采集到的兩幅圖像角點信息，確定待匹配角點間相對位置關系的過程，在數字圖像處理、計算機視覺以及和模式識別等領域有重要應用價值。目前已提出了許多角點匹配算法，其中基于圖像點特征及灰度信息的角點匹配算法[1]，利用局部灰度相關實現角點匹配；基于位置相似性特征的角點匹配算法[2]，利用局部范圍內對應點的相對位置不變作為約束條件實現角點匹配；基于Hausdorff距離的角點匹配[3]，利用待匹配角點間的Hausdorff距離實現角點匹配；基于圖像亮度相關的角點匹配[4]，利用光流法與一階差分技術實現角點匹配；基于確定性退火技術魯棒性點匹配算法[5]，利用匹配矩陣估計方法構造自由能函數，最終實現角點匹配。

在圖像采集過程中，由于拍攝角度不同會導致圖像在空間上存在平移、旋轉等差異，這些差異會影響角點匹配的精度。由于仿射變換[6]能夠有效獲取圖像間的平移和旋轉參數，從而可以消除平移旋轉等對角點匹配的影響。通過仿射變換的同素性與平行性可將角點匹配過程轉化為求解角點間仿射變換參數的過程。為此本文將角點檢測與確定性退火技術[7]相結合，利用角點檢測時生成自相關矩陣梯度信息構造退火過程的自由能函數，并運用確定性退火技術自由能函數收斂到全局最優解的性質，對角點匹配自由能函數進行優化處理，獲取兩匹配圖像角點間的仿射變換參數，最后通過該參數實現角點匹配。

2 角點匹配流程

提出的角點匹配流程如圖1所示。首先利用Harris算子[8]對目標和模板圖像分別進行角點檢測，然后將確定性退火技術應用于角點匹配過程中，通過構造自由能函數與優化自由能函數獲取待匹配角點間的仿射變換參數，最后利用該參數實現角點匹配。

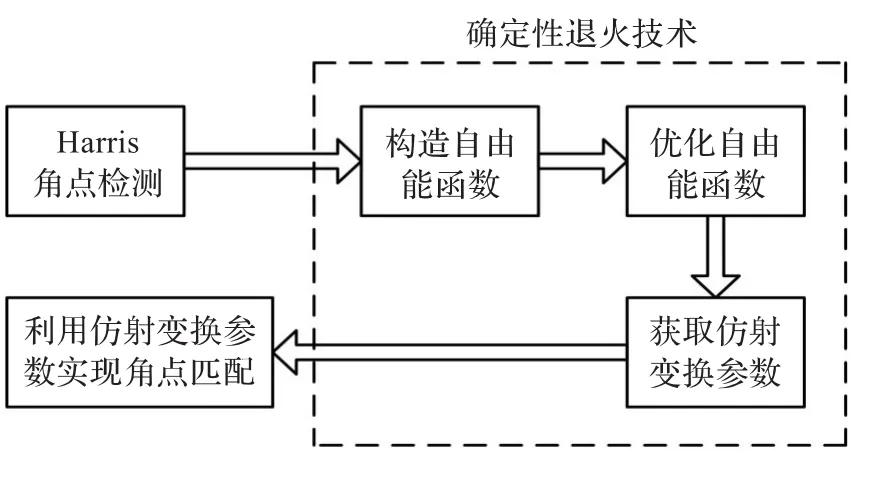
圖1 角點匹配流程圖

3 Harris角點檢測

Harris角點檢測[9]是基于圖像灰度的檢測，通過計算像素點所在位置的梯度變化來檢測角點，若像素點所在位置x方向梯度與y方向梯度的絕對值均較大，則將該像素點判定為角點。

其中detM=λ1×λ2，trM是矩陣M的跡，且trM=λ1+λ2，k為大于零的參數。通常，detM在邊緣處較小而在角點處較大，而trM在邊緣和角點處則保持一致。因此，當像素點(x，y)的Rh值為局部最大時，即為角點。

4 仿射變換參數確定

當獲取目標和模板圖像的角點信息后，如何對角點進行匹配直接關系到匹配精度。由于目標圖像可能存在平移旋轉，因此如何獲取最優的仿射變換參數是實現匹配結果的關鍵，求得的仿射變換參數一方面應能消除平移旋轉的影響，另一方面應能保證更多的匹配點數。為此，本文運用確定性退火過程來獲取最優仿射變換參數。

確定性退火技術是依據自然法則提出的一種求解全局最優解的擬自然方法，將求解一系列隨溫度變化的物理系統自由能函數極小值思想引入到求解優化問題，它能使算法直接得到全局極小值，無需考慮局部極小值對優化問題的影響。

退火過程利用自由能減少定律描述系統在每一溫度下達到平衡態的過程。由自由能減少定律可得：

其中E(x)是指某一物理系統的能量，當系統達到平衡狀態時自由能函數達到極小值。確定性退火技術要求構造物理系統式（2）對應的自由能函數F(x，T)。此函數F(x，T)應滿足：

（1）當T=∞時，F(x，T)的全局極小值易求出。

（2）當T=0時，F(x，T)=E(x)。確定性退火技術就是將系統在T=T+ΔT時的自由能函數的極小值xmin(T+ΔT)作為初始值，通過求解m inF(x，T)的極小值來模擬系統達到平衡狀態的過程。確定性退火的求解過程如下：

步驟1確定系統自由能函數F(x，T)，使F(x，T)滿足上述兩個條件。

步驟2初始化T=T0，記xmin(Tk)為m inF(x，Tk)的最優解。

步驟3Tk+1=αTk(0＜α＜1)，以xmin(T0)為初始值求解m inF(x，Tk+1)，記相應最優解為xmin(Tk+1)，其中α為退火速率。

步驟4判斷Tk是否收斂，若滿足則停止，則xmin(Tk+1)為最優解，否則執行下一步。

步驟5k=k+1，執行步驟3。

4.1 自由能函數構造

能否構造出合適的自由能函數是角點匹配的關鍵，構造出的自由能函數應包含待匹配角點間的仿射變換參數。為了求取最優仿射變換參數，將仿射變換與角點檢測中自相關矩陣梯度[10]信息結合構造自由能函數。

仿射變換的一般表達式為：

其中PA={(xa1,ya1),(xa2,ya2),(xa3,ya3),…,(xam,yam)}和PB= {(xb1，yb1)，(xb2，yb2)，(xb3，yb3)，…，(xbn，ybn)}，分別表示目標圖像與模板圖像中待匹配的角點坐標，A是旋轉矩陣，T為平移矩陣。旋轉和平移參數矩陣決定了待匹配角點間的坐標變換關系。設V為仿射變換算子，則二維空間的仿射變換可表示為：

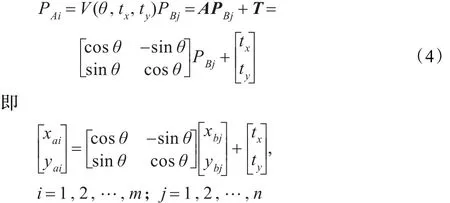
其中θ為旋轉角度，tx，ty為平移量。

由角點檢測自相關矩陣M可知，XY梯度算子包含了水平與垂直方向的梯度信息。因此利用X和Y的乘積重新描述每一個角點。假設GXY為某一角點在水平與垂直方向的梯度值之積，則可將通過仿射變換后的目標圖像與模板圖像角點的GXY絕對值差之和GXY作為角點是否匹配的依據，即：

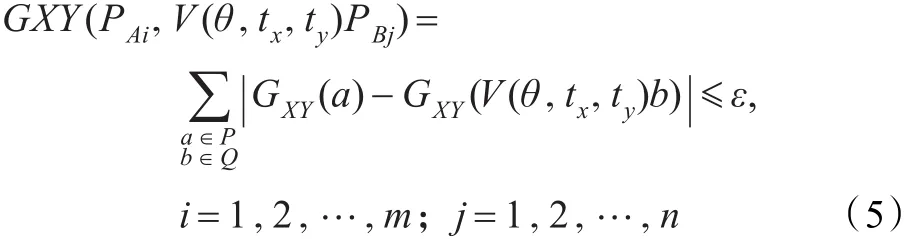
其中P與Q是兩個ω×ω大小的窗口，其中心位于待匹配角點，ε為給定閾值，a和b分別是P與Q中的角點。當GXY值最小時，則可以判定兩個角點匹配。

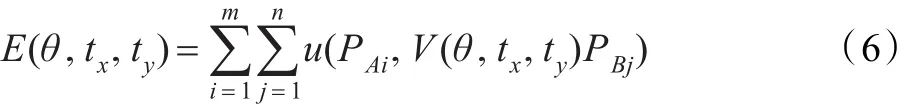
E(θ，tx，ty)值表征在仿射變換V的作用下，兩個角點集PA與PB的匹配點數。物理退火過程的自由能函數采用Boltzman概率分布，其分布表示為：

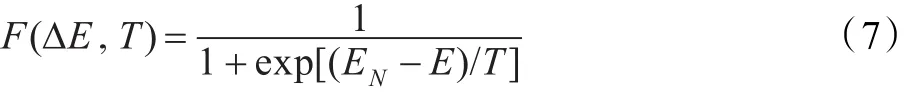
其中，EN為新能量值，E為原始能量，T為溫度值，ΔE=EN-E。

根據能量函數可以構造出如下函數：

由于F(θ，tx，ty，T)具有上述兩個性質，因此可以將其作為角點匹配時的自由能函數。

4.2 自由能函數優化

自由能函數優化的目的是為了求取最優的仿射變換參數，利用該參數對待匹配點集進行匹配，獲得角點集之間的對應關系實現角點匹配。

自由能函數優化處理步驟如下：

步驟1退火系統初始化：T=T0，θ=θ0，tx=tx0，ty=ty0，系統最小溫度Tmin，系統退火速率α。

步驟2自由能函數的優化：當系統溫度T≥Tmin時，利用共軛梯度算法對自由能函數進行處理，求得一組平移與旋轉參數，然后將系統溫度T乘以退火速率α作為新的系統溫度T，與系統最小溫度Tmin進行比較，若T≥Tmin，則繼續上述處理；否則停止運算，并輸出自由能函數最小值：m inF(θ，tx，ty，T)=V(θ，tx，ty)，此時獲取的(θ，tx，ty)為最優仿射變換參數。

步驟3利用最優仿射變換參數對PB中的點進行坐標變換得到PB'，將PA與PB'中的點進行匹配，其中PB'=V(θ，tx，ty)PB。

5 角點匹配

角點匹配的目的是確定待匹配角點間的對應關系，利用Harris角點檢測算法分別獲取待匹配圖像的角點后，運用自由能函數優化求取的最優仿射變換參數對角點進行匹配。具體步驟如下：

步驟1利用自由能函數最小化求取最優仿射變換參數V(θ，tx，ty)，對PB進行仿射變換得到PB'。

步驟2利用式（5）將待匹配角點進行比較，當GXY的值達到最小時，則判定兩個角點匹配。

步驟3所有待匹配角點依次執行步驟2，完成角點匹配。

6 實驗結果

為了驗證方法的有效性，在MATLAB平臺上進行了仿真。模板圖像和目標圖像均為420×255像素大小，圖2（a）和（b）分別為模板和目標圖像，圖2（b）相對于圖2（a）存在平移和旋轉現象。首先利用Harris算法對兩幅圖像進行角點檢測，結果如圖2（白色十字為檢測出的角點）所示。

圖2 Harris算法角點檢測結果

利用本文方法對檢測到的角點進行匹配，其中閾值ε=1，初始值T0=100，θ=0°，tx=0，ty=0，Tmin=0.1，退火速率α=0.8，匹配所選用窗口大小為5×5（通常取奇數對），通過自由能函數優化后得到的仿射變換參數為：θ=13°，tx=46 pix，ty=9 pix。角點匹配結果如圖3所示，其中白色十字為匹配角點。

圖3 本文角點匹配方法

為了驗證該方法性能，在圖2角點檢測的基礎上，分別采用基于Hausdorff距離[11]的角點匹配和基于歸一化互相關（NCC）[12]的角點匹配方法進行了角點匹配，匹配結果分別如圖4和圖5所示。可以看出，本文方法的匹配點數（具體如表1）明顯多于其他兩種方法。這表明在利用仿射變換參數實現角點匹配時，本文方法充分利用了圖像的特征信息，獲取了最優的仿射變換參數。

圖4 基于Hausdorff距離的角點匹配

圖5 基于歸一化互相關的角點匹配

從表1也可以看出，本文方法的運算復雜度低于Hausdorff距離的角點匹配，但高于NCC角點匹配方法，但匹配效果明顯優于其他兩種方法。

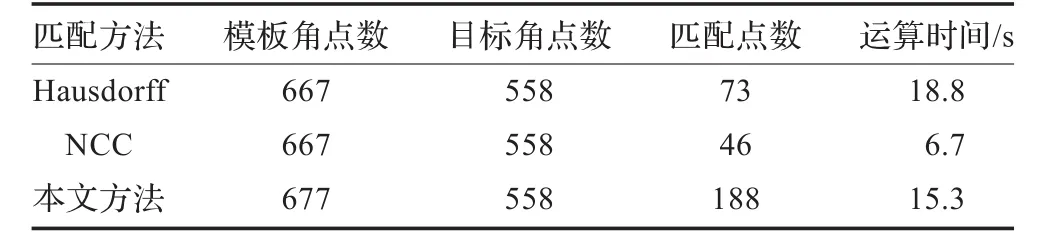
表1 不同匹配方法的匹配點數及運算時間對比

7 結論

對于圖像角點匹配過程中由于目標圖像存在平移旋轉對匹配造成的影響。將角點檢測時生成的自相關矩陣梯度信息與仿射變換結合，通過確定性退火過程中的自由能函數構造以及優化獲取最優的仿射變換參數，并以此實現角點匹配。通過自相關矩陣的梯度信息構造自由能函數，充分利用了圖像中的特征信息，在一定程度上降低了構造自由能函數的復雜度。由于獲取了最優的仿射變換參數，因而匹配效果較好。

[1]曹曉光，徐琳，郁文霞.基于角點檢測的高精度點匹配算法[J].儀器儀表學報，2006，27（6）：1269-1271.

[2]潘俊君，張艷寧.相關視覺中基于位置相似性特征的點匹配問題研究[J].中國圖象圖形學報，2005，10（1）：80-86.

[3]Huttenlocher D P，K landerman G A，Rucklidge W J.Comparing image using the Hausdorff distance[J].IEEE Trans PAM I，1993，15（9）：850-863.

[4]Georgescu B，Meer P.Point matching under large image deformations and illum ination changes[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2004，26（6）：647-688.

[5]孫東梅，裘正定.基于確定性退火技術的魯棒性點匹配算法[J].計算機學報，2002，25（6）：606-611.

[6]Aw rangjeb M，Lu Guojun.An improved curvature scale-space corner detector and a robust corner matching approach[J]. IEEE Transactions on Image Processing，2008，17（12）：2425-2441.

[7]楊廣文，李曉明.確定性退火技術[J].計算機學報，1998，21（8）：765-768.

[8]Harris C，Stephens M.A combined corner and edge detector[C]// Proceedings of the 4th A lvey Vision Conference，Manchester，1988：147-151.

[9]趙萬金，龔聲蓉.一種自適應的Harris角點檢測算法[J].計算機工程，2008，34（10）：212-214.

[10]Alkaabi S，Deravi F.Iterative corner extraction and matching for mosaic construction[C]//Proceeding of 2nd Computer and Robot Vision，British Columbia，Canada，2005：468-475.

[11]孫瑾，顧宏武.一種魯棒性Hausdorff距離圖像匹配方法[J].中國圖像圖形學報，2008，13（4）：761-767.

[12]郭偉，趙亦工.一種改進的紅外圖像歸一化互相關匹配算法[J].光子學報，2009，38（1）：189-193.

WANG Xiaopeng,FANG Chao,LEI Tao

School of Electronic&Information Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China

During the course of image corner matching,the translation and rotation of object image often affect the matching results.A corner matching method is proposed based on deterministic annealing.Harris corner detection is used to extract the corner points respectively from object and matching image,and the gradient information of the corner points from the autocorrelation matrix are also calculated.The free energy function of deterministic annealing is constructed by combining the gradient information and the affine transform.The optimization affine transform parameters are obtained by optimizing the free energy function.Corner matching between object and matching image are complemented through the affine transform.Simulations show that this method can effectively achieve the corner matching when the object image occurring translation and rotation.

corner matching;translation and rotation;deterministic annealing;affine transform

A

TP391.4

10.3778/j.issn.1002-8331.1209-0290

WANG Xiaopeng,FANG Chao,LEI Tao.Corner matching for translation and rotation image.Computer Engineering and Applications,2014,50（16）：173-176.

國家自然科學基金（No.61261029，No.61202314）；甘肅省高等學校碩士生導師科研項目（No.1104-4）。

王小鵬（1969—），博士，教授，研究方向：圖像分析與識別；房超（1987—），碩士研究生，研究方向：圖像處理；雷濤（1981—），博士，副教授，主要研究方向：數字圖像分析。E-mail：wangxp1969@sina.com

2012-09-25

2012-11-08

1002-8331（2014）16-0173-04

CNKI網絡優先出版：2012-12-18,http://www.cnki.net/kcms/detail/11.2127.TP.20121218.1528.023.htm l