基于標準系數法的空間系繩系統狀態保持穩定控制*

李 超 王長青 李愛軍 扎伯羅特諾夫.尤里

1.西北工業大學自動化學院國際空間系繩系統研究中心，西安 7100722.薩馬拉國立航空航天大學，俄羅斯薩馬拉

基于標準系數法的空間系繩系統狀態保持穩定控制*

李 超1王長青1李愛軍1扎伯羅特諾夫.尤里2

1.西北工業大學自動化學院國際空間系繩系統研究中心，西安 710072
2.薩馬拉國立航空航天大學，俄羅斯薩馬拉

首先基于啞鈴模型建立空間系繩系統的數學模型，然后對標準系數法進行了介紹，在此基礎上提出了基于標準系數法的空間系繩系統狀態保持穩定控制算法，最后結合仿真實例對空間系繩系統的狀態保持穩定控制進行了分析，并與線性最優二次型設計方法進行了比較，同時還對系統的魯棒性進行了研究。結果表明使用標準系數法設計的控制系統不僅能夠達到控制要求，而且設計簡單，所得出的控制系統具有良好的魯棒性。

標準系數法;空間系繩系統;啞鈴模型;狀態保持;穩定控制

空間系繩系統是指用柔性系繩將2個或2個以上的航天器連接在一起所構成的空間飛行系統［1］。自1895齊奧爾科夫斯基提出“赤道通天塔”的設想以來，美國、俄羅斯、意大利等多個國家進行了大量的研究和實驗［2］。該系統具有廣闊的應用前景［3-5］:從基站飛船上發射小衛星、監測高空大氣層、軌道機動、依靠系繩返回艙從軌道上回收有效載荷、清理太空垃圾等。

系繩系統執行的主要科學探測活動大多是在狀態保持階段進行的。但是復雜的太空環境會給系統帶來干擾，甚至會影響系統正常工作。因此，需要一定的控制策略將系統快速控制到穩定狀態。Larsen等設計了一套非線性控制器，并利用電動繩注入阻尼的方法將系繩衛星系統控制到一個漸進穩定的平衡位置［6］。Mankala等設計了一套邊界控制器將系統控制到徑向相對平衡位置［7］。Pasca研究了系繩衛星系統在狀態保持階段的運動，并提出了利用子星推力來控制系繩的面內振蕩［8］。Fujii等人在不考慮系繩的徑向振動時，提出了一種波動合并控制方法來抑制系繩的橫向振動［9］。國內的Yong He等通過對系統在平衡點穩定性的分析推導出了一種速率控制方法［10］。劉麗麗等研究了系繩系統在狀態保持階段的混沌運動［11］。上述文獻主要針對如何將系繩系統控制到平衡位置以及研究狀態保持階段的運動。

本文采用在控制工程領域有較好應用的標準系數法［12-13］來對空間系繩系統狀態保持穩定控制進行研究。它避免了復雜的優化算法，把控制系統的設計轉化為簡單的代數運算，大大簡化了控制系統的設計。

1 模型建立

采用啞鈴模型，假設系繩為剛性繩，質量不計，忽略在拉力下產生的形變，將主星和子星看作質點，主星、子星及系統總質量分別為m1，m2，m=m1+m2，并且主星質量m1遠遠大于子星質量m2，所以認為系統質心在主星上。在軌道坐標系下建立系統的動力學方程［14］:

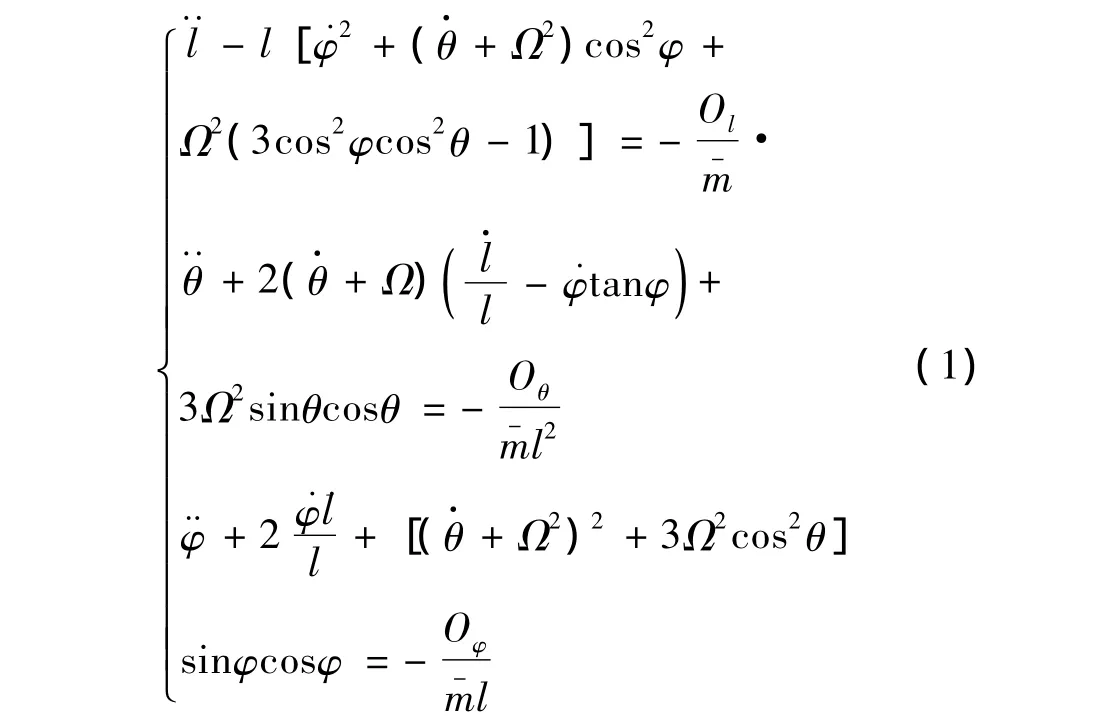
為了方便研究，不考慮面外角的影響。因此系統方程(1)可以簡化為

其中，T為系繩的拉力。

2 標準系數法

目前主要的標準系數法有:牛頓二項式標準型、ITAE標準型、Butterworth標準型以及各種標準型的改進型。與其他標準型相比，ITAE標準型性能指標具有較好的實用性和選擇性。因此，本文選擇采用ITAE標準型對空間系繩系統進行研究。

表1給出了ITAE標準型一到八階系統的標準特征多項式的形式。其中特征參數ω0的選擇具有較大的靈活性，通常是根據所要設計系統的性能要求來選擇。如果事先沒有給出系統的動態性能指標，ω0的選擇就有較大的范圍，可以根據具體情況而定。

表1 1～8階系統的標準特征多項式

3 空間系繩系統狀態保持穩定控制算法

基于標準系數法的空間系繩系統狀態保持穩定控制算法如下:

1)將空間系繩系統的動力學方程進行線性化處理，得出其狀態方程

把方程(2)量綱歸一化，并在平衡點附近線性化得:

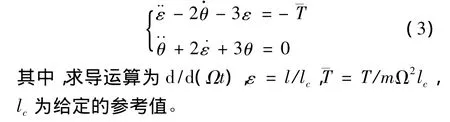
把系統方程寫成狀態空間的形式，即:

2)寫出系統的開環與閉環傳遞函數

系繩系統的狀態保持穩定控制結構圖如圖2所示，令C為單位矩陣。

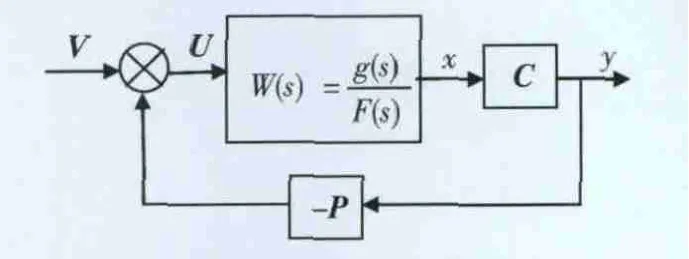
圖1 系統狀態反饋結構圖

系統的開環傳遞函數為:

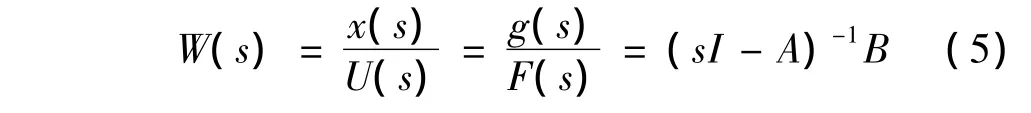
系統的閉環傳遞函數為:

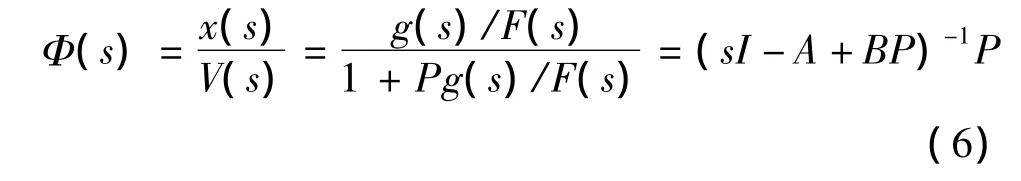
3)將開環傳遞函數寫成分式形式

將式(5)寫成如下分式形式:

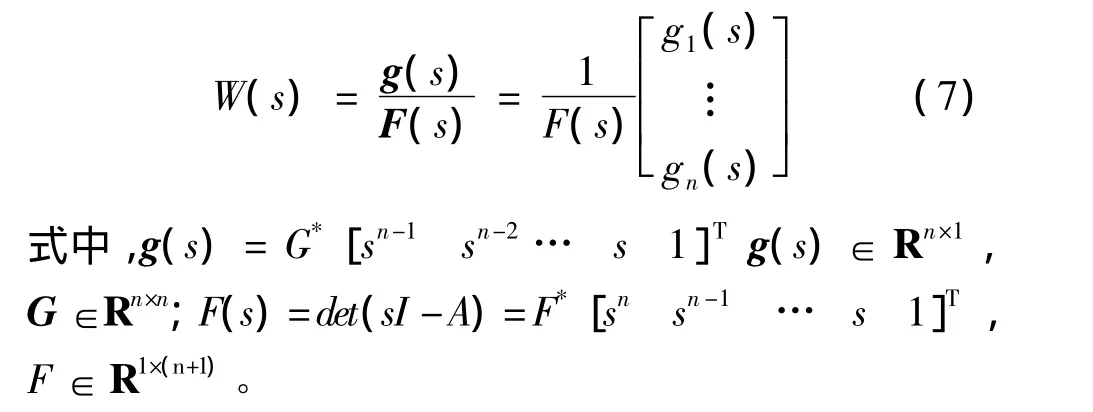
代入數據，計算得系統特征多項式F(s)和分子多項式g(s)的系數矩陣F，G分別為:

4)寫出閉環系統的特征方程，選取標準系數特征多項式

根據步驟2)的閉環傳遞函數式(6)，系統特征方程為:

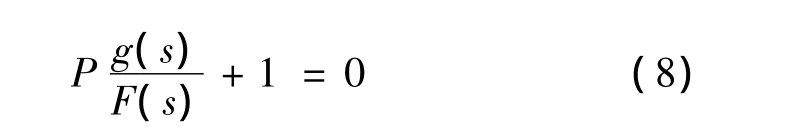
將式(8)進行通分，令分子等于標準特征多項式H(s)，得到下面的關系式:

本系統為4階系統，在表1中選取標準特征多項式H(s)，其系數矩陣H為:

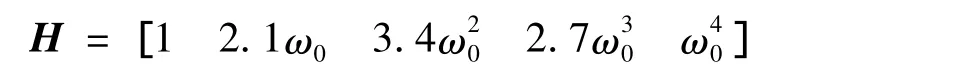
5)選取ω0，求解控制器系數矩陣P

在式(9)中只有矩陣P是未知的。令關系式左右s相同指數的系數對應相等，得到一個方程組，選擇適當的ω0，解方程組就可以求出控制器系數矩陣P的所有元素。

本文取ω0=1．5，求解控制器系數矩陣P的代數方程組得:

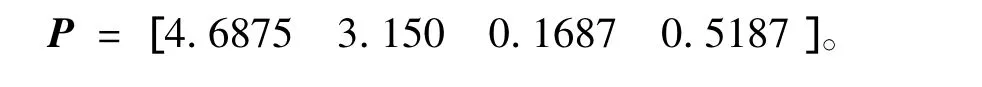
4 仿真分析

取系統的初始面內角θ=-0．1°，=0．1，系繩系統穩定保持的動態特性仿真結果如圖2所示。

由圖2可以看出，繩長、繩長變化率、面內角和面內角變化率都在6s內回到穩態值，此時系繩系統又穩定到平衡狀態。在系統恢復到平衡狀態時，雖然系統有一定的振蕩，但是振蕩都非常小，其最大振幅分別為 1.054，0.06，0.062，0.1665。

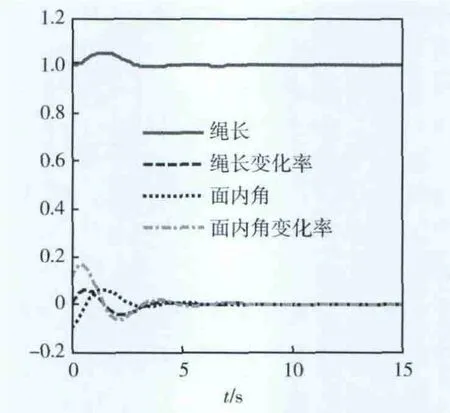
圖2 基于標準系數法的狀態保持穩定控制

4.1 與線性二次型最優控制方法的比較

針對空間系繩衛星系統在穩定狀態附近的線性化模型，也可以采用線性二次型最優控制來設計控制律。在該方法中狀態變量和輸入變量的加權矩陣Q，R的選擇非常重要。本文中取 Q=diag(5，5，30，30)，R=1，得最優化反饋增益矩陣:

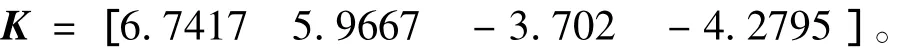
在相同的攝動下，系繩系統穩定保持的動態特性仿真結果如圖3所示。

圖3 基于LQR方法的狀態保持穩定控制

由圖3可以看出，基于LQR方法設計的控制系統其繩長、繩長變化率、面內角和面內角變化率也都在6s內回到穩態值。在系統恢復到平衡狀態時，系統過渡比較平穩，沒有太大的振蕩，其最大振幅分別為 1.083，0.102，0.031，0.149。

圖4為2種設計方法控制效果比較圖，其中虛線表示采用標準系數法設計的控制系統的控制效果圖;實線表示采用LQR方法設計的控制系統的控制效果圖。由圖4可以看出，使用標準系數法設計的控制系統能夠達到LQR設計方法的控制效果。

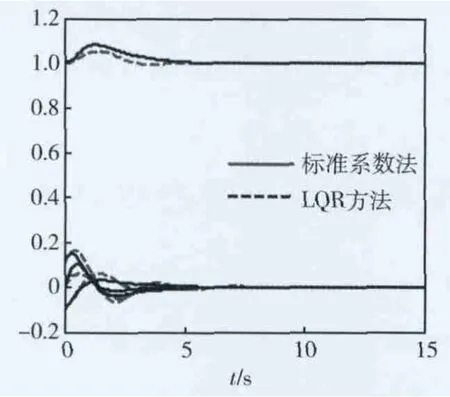
圖4 2種設計方法控制效果比較

4.2 魯棒性分析

系繩系統處于太空中，因此會受到太空碎片、極端溫度等各種外界因素的影響，所以系統參數會有一定的攝動，這表現為系統方程中A，B陣的變化。當系統初始面內角為-0.1°時，研究系繩系統狀態保持動態特性的魯棒性。

圖5～7分別表示A陣、B陣以及A陣和B陣同時變化±20%時系繩系統狀態保持的被控變量θ的動態特性曲線。其中實線表示系統具有+20%攝動時的仿真結果，虛線表示系統沒有攝動時的仿真結果，點線表示系統具有-20%攝動時的仿真結果。由圖可以看出，當系統受到+20%攝動時，θ的最大振幅增加量在0.015°以內;當系統受到-20%攝動時，θ的最大振幅增加量在0.01°以內。由此可見，基于標準系數法的設計方法設計的控制系統具有良好的魯棒性。

圖5 A陣變化±20%時系繩系統狀態保持的動態特性

5 結論

在簡化的系繩系統模型下，不考慮系繩的面外運動，通過標準系數法來設計系繩系統狀態保持穩定控制器。仿真結果表明這種方法與線性二次型最優化設計方法的控制效果相當，但比二次型優化設計方法簡單，且得出的結果具有良好的魯棒性。研究結果對未來空間系繩系統控制器的設計提供了一定的參考。

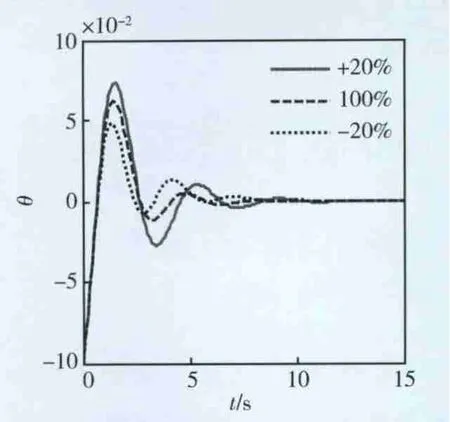
圖6 B陣變化±20%時系繩系統狀態保持的動態特性

圖7 A，B陣同時變化±20%時系繩系統狀態保持的動態特性

［1］孔憲仁，徐大富.空間繩系研究綜述［J］.航天器環境工程，2010，27(6):0775-0783.(Kong Xianren，Xu Da fu.The Studies of Space Tether［J］.Spacecraft Environment Engineering，2010，27(6):0775-0783.)

［2］王長青，董哲，李愛軍，張叢叢.空間系繩系統實驗研究綜述［C］.中國制導、導航與控制學術會議，北京航空航天大學，2012.(Wang Changqing，Dong Zhe，Li Aijun，Zhang Congcong.The Overview of Space Tether System Experiments［C］.Chinese Gudiance，Navigation and Control Conference，Bei Hang University，2012.)

［3］鄭鵬飛，曹喜濱，張世杰.大氣阻力攝動下的繩系輔助離軌系統的相對姿態跟蹤控制研究［J］.航天控制，2009，27(4):8-13.(ZHENG Pengfei，CAO Xibin，ZHANG Shijie.Relative Attitude Tracking Control of Tether-assisted Deorbit System Under Drag Perturbation［J］.Aerospace Control，2009，27(4):8-13.)

［4］張玉軍，馮書興.主動式空間碎片清理研究［J］.裝備指揮技術學院學報，2010，21(6):78-82.(Zhang Yujun，Feng Shuxing.Research on Active Space Debirs Removal［J］.Journal of the Academy of Equipment Control＆ Technology，2010，21(6):78-82.)

［5］馮杰，鮮勇，雷剛，魏鵬濤.繩系衛星實施安全捕獲的能量最優控制［J］.航天控制，2011，29(4):66-70.(FENG Jie，XIAN Yong，LEI Gang，WEI Pengtao.Energy-optimal Control of Safe Capture by Using Tethered Subsatellite［J］.Aerospace Control，2011，29(4):66-70.)

［6］Larsen M B，Blanke M.Control by Damping Injection of Electrodynamic Tether System in an Inclined Orbit［C］.The 2009 American Control Conference，USA，2009.

［7］Mankala K K，Agrawal S K.A Boundary Controller Based on Linear Infinite Dimensional System for Station Keeping of a Tethered Satellite System［C］.The 2006 American ControlConference， Minneapolis， USA，2006.

［8］Pasca M.Nonlinear Control of Tethered Satellite System Oscillations［J］.Nonlinear Analysis:Theory，Methods and Applications，1997，30(6):3867-3878.

［9］Fujii H A，Watanabe T，Trivailo P M.Wave-absorbing Control of Transverse Vibration of Tether Systems［J］.Journal of the Astronautical Science，2003，51(3):249-259.

［10］He Yong，Liang Bin，Xu Wenfu.Study on the Stability of Tethered Satellite System ［J］.ActaAstronautica，2011，(68):1964-1972.

［11］劉麗麗，金棟平，胡海巖.狀態保持階段繩系衛星的混沌運動［C］.全國非線性振動學術會議，北京，2007.(Liu Lili，Jin Dongping，Hu Haiyang.Chaotic Oscillations of A Tethered Satellite in the Station Keeping Phase［C］.The Nonlinear Vibration of Academic Meeting，Beijing，2007.)

［12］王長青，李愛軍，王偉.Butterworth濾波器在飛行控制系統中的應用［J］.飛行力學，2009，27(1):74-76.(Wang Changqin，Li Aijun，WangWei.Application of Butterworth Filter to Design of Flight Control Systems［J］.Flight Dynamics，2009，27(1):74-76.)

［13］李晉堯，張明鳴，王燕.基于ITAE的高精度無超調溫度校驗設備［J］.儀器儀表學報，2008，29(4):497-500.(Li Jinyao，Zhang Mingming，Wang Yan.Hight Accuracy Non-overshooting Temperature Calibrator Based on ITAE［J］.Chinese Journal of Scientific Instrument，2008，29(4):497-500.)

［14］扎伯羅特諾夫·尤里，著.空間系繩系統運動動力學與控制導論［M］.王長青，等.譯.北京:科學出版社，2013.

Stability Control for Station-Keeping Phase of Space Tether System Based on Standard Coefficient Method

LI Chao1WANG Changqing1LI Aijun1ZABOLOTNOV Yuriy2
1.International Research Center of Space Tether System，College of Automation，Northwestern Polytechnical University，Xi’an 710072，China
2.Samara State Aerospace University，Samara，Russia

Firstly，the mathematical model of space tether system based on the dumbbell-shaped model is established．Then，the standard coefficient method is briefly described，and detailed discussion follows on how to design the controller．Finally，by employing simulation cases，the steady control of space tether system is analyzed，and also simulation results are given by comparing the method proposed in this paper with the well-known linear quadratic regulator method．At the same time，the robustness of the control system is studied．The simulation results show that the controller based on the standard coefficient method can achieve the requirement of control system while it is simpler than the linear quadratic regulator method and the control system also has good robustness．

Standard coefficient method;Space tether system;Dumbbell-shaped model;Station-keeping phase;Stability control

V448.2

A

1006-3242(2014)02-0073-05

*2011年度國家國際科技合作專項資助;陜西省科學技術研究發展計劃項目(2013KW09-02)

2013-09-24

李 超(1986-)，男，河南鶴壁人，碩士研究生，主要研究領域為飛行器控制與仿真、空間系繩系運動動力學與控制等;王長青(1973-)，男，黑龍江富錦人，博士，副教授，主要研究領域為飛行器控制與仿真、空間系繩系統運動動力學與控制等;李愛軍(1972-)，男，黑龍江密山人，博士，教授，主要研究領域為飛行器控制與仿真、空間系繩系統運動動力學與控制等;扎伯羅特諾夫·尤里(1952-)，男，俄羅斯宇航科學院院士，薩馬拉國航空航天大學教授，西北工業大學高端外國專家，主要研究領域為空間系繩系統運動動力學與控制。