海拔高度與大氣壓關系的回歸計算

王麗莉WANG Li-li

（蘭州城市建設學校，蘭州730046）

在一些特殊工作中，需要根據海拔高度計算大氣壓的數值。本文根據全國主要城市的海拔高度與大氣壓數值，回歸計算出了比較準確的海拔高度與大氣壓數值的實際關系，可供參考使用。

例如，使用全站儀在某個海拔高度的地區進行測量工作時，許多國產儀器需要輸入該地區的大氣壓數值，由儀器的計算系統準確地進行大氣壓值改變所引起的距離測量改正值，以保證得到準確的測量成果。

在百度文庫提供的“全國各地主要城市海拔高及大氣壓參考數據”表中，共有203個城市的海拔高及大氣壓實際數據。

將海拔與氣壓數據在CAD上按二維坐標展點，分布形成一條曲線。在CAD圖中，北京、香港、吐魯番、北海、恩施、甘孜、索縣7個城市的數據明顯偏離曲線，將這203組數據在EXCEL電子表中排序，按照數據處理原則，這7組觀測值應該是帶有粗差。所以，剔除這7組數據，用其余196組數據進行了回歸計算。經過多種試算，海拔高度H(m)與大氣壓P(kPa)的關系最為符合下邊的曲線形式：

P=aebH

將該式兩邊取自然對數：lnP=lna+bHlne

因為lne=1，該式即為：lnP=lna+bH

進行變量替換，設：y=lnP A=lna B=b x=H

則曲線方程化為線性方程：y=A+Bx

該線性方程需要確定A、B參數。進行二元回歸計算，按最小二乘法原理，可導出兩個標準方程為：

用196組數據在EXCEL電子表中計算∑y、∑x、∑x·y、∑x2，由于篇幅原因，表中計算過程數據略，結果如下：

∑y=890.874206253463

N=196

將上列數值代入（1）、（2）式整理即有：

聯解（3）、（4）式可得：

A=4.610770904

B=-0.000117

則由A=lna與B=b可得：

a=e4.610770904=100.56

b=B=-0.000117

即有

式中：高程H單位為m，氣壓P單位為kPa。

關于海拔高度（H）與大氣壓值（P）的關系，在網上能查到一種簡單的計算方法：

式中：高程H單位為m，氣壓P單位為Pa。

另外，在網上還能查到一種比較復雜的計算方法：

式中：高程H單位為m，氣壓P單位為Pa。

根據回歸計算理論，標準離差的計算式可以表示為：

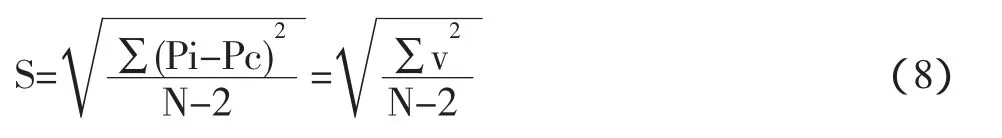
運用196組數據在EXCEL電子表中，根據高程H，分別用（5）、（6）、（7）式計算出大氣壓 P 的數值，并統一化成以kPa單位一，計算標準離差，計算過程數據略，結果如下：

由（6）式計算P Σvv=336.2814；

由（7）式計算P Σvv=95.2391；

由（5）式計算P Σvv=2.54065。

由（6）式根據高程計算196組數據的大氣壓值P，其標準離差為：

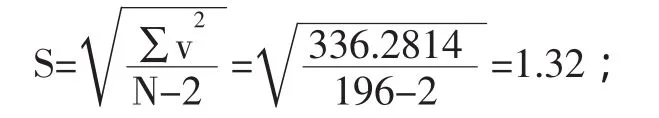
由（7）式根據高程計算196組數據的大氣壓值P，其標準離差為

由（5）式根據高程計算196組數據的大氣壓值P，其標準離差為

顯然，按（5）式根據高程計算出的大氣壓數值，標準離差最小，只有0.11kPa，說明按照回歸計算出的（5）式計算海拔高度H與大氣壓P的數值關系是比較準確的。

需要說明的是，由于“全國各地主要城市海拔高及大氣壓參考數據”表中，給出的海拔高度最大的城市是西藏的那曲，數值為4507m。因此，（5）式應該適用于4500m以下的地區，對于4500m以上的地區，還有待獲得相應海拔高度的實際數據后，再進行計算驗證。

值得一提的是，由回歸計算出的（5）式計算可知，平常所說的海平面上的大氣壓強是1013.25kPa并不準確。由（5）式計算的結果是，當海拔高度為-64.8m時，大氣壓強才是1013.25kPa。在“全國各地主要城市海拔高及大氣壓參考數據”表中，天津、寧波、崇明、汕頭、西沙、連云港等十幾個城市的海拔高度都在10m以下，極接近海平面，這些城市的數據都是（5）式的有力支撐。

[1]周銀河，嚴薇.建筑經濟與企業管理[M].武漢：武漢大學出版社，2001.

[2]方小兵.大氣壓與高度關系的再討論[J].安康師專學報，2005(01).

[3]柳福提.大氣溫度隨高度變化率的推導[J].河南科技學院學報(自然科學版)，2007(02).