廣義代數(shù)幾何碼探究

王 貞

（池州學(xué)院 數(shù)學(xué)與計算機(jī)科學(xué)系，安徽 池州247000）

廣義代數(shù)幾何碼探究

王 貞

（池州學(xué)院 數(shù)學(xué)與計算機(jī)科學(xué)系，安徽 池州247000）

廣義代數(shù)幾何碼是通過有限域上的代數(shù)函數(shù)域中一些次數(shù)較低的位而得到的一種碼。在此基礎(chǔ)上,通過構(gòu)造函數(shù)域碼和廣義代數(shù)幾何碼的子域子碼，從而得到參數(shù)更好的線性碼。

位；代數(shù)幾何碼；函數(shù)域碼；子域子碼

1 引言

20世紀(jì)70年代，Goppa[1]首先利用有限域上的代數(shù)曲線來構(gòu)造碼。20世紀(jì)80年代初，Tsfasman[2]等人將Goppa思想與代數(shù)幾何相結(jié)合，構(gòu)造出一系列糾錯碼，使其信息率超過Gilbert-Varshamov界。代數(shù)幾何碼主要利用有限域上代數(shù)曲線的有理點(diǎn)構(gòu)造線性碼。對于有限域，當(dāng)較小時，建立在其上的代數(shù)曲線的有理點(diǎn)很難構(gòu)造出好的代數(shù)幾何碼。由于這樣的局限性，人們嘗試用次數(shù)高于1的位去構(gòu)造線性碼，并取得了好的漸近系數(shù)[3-4]。

Xing[5]通過高次數(shù)級聯(lián)碼構(gòu)造廣義代數(shù)幾何碼，將代數(shù)幾何碼進(jìn)行推廣，并且得到非常好的線性碼。本文在此基礎(chǔ)上，通過構(gòu)造其子域子碼，得到參數(shù)更好的線性碼。

2 預(yù)備知識

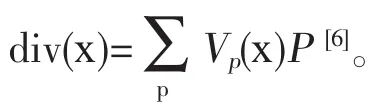
對于任意一個Fr(x)中除子G，向量空間

是一個有限維線性空間，由Riemann-Roch定理[6],

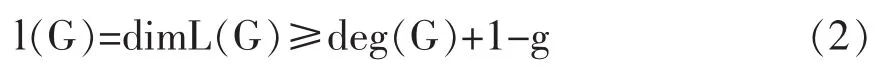
其中g(shù)為x的虧格。當(dāng)deg（G）≥2g-1時，（2）式取等號。

令P1，P2， …，Ps為x上s個互不相同的位，deg(Pi)=ki，1≤i≤s，且滿足supp(G)∩{P1，P2，…，Ps}=.

定義1[7]函數(shù)域碼是Fr(x)一個非零有限維的Fr線性子空間V滿足：

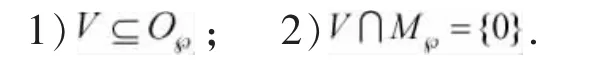
Ci表示r元線性碼[ni，ki=deg（Pi）,di],1≤i≤s。 πi表示Fr上Frki到Ci的單同態(tài)。令

定義2[5]上述映射α的象稱為廣義代數(shù)幾何碼，記為C（P1，P2，…Ps；G；C1，…Cs）.

當(dāng)Pi為有理位時，有ni=ki=di=1，1≤i≤s，C（P1，P2，…Ps；G；C1，…Cs）為Goppa代數(shù)幾何碼。

3 主要結(jié)論

令C是Fr上線性碼[N0，K0，D0]，為Fq上線性碼[N0，K0，D0]，C|Fq稱為C的子域子碼，k0≥sK0-（s-1）N0，d0≥D[8]。 從而得到：

定理3 設(shè)C（P1，P2，…Ps；G；C1，…Cs）為來自函數(shù)域碼V（G）的廣義代數(shù)幾何碼[N，K，D]，C（P1，P2，…Ps；G；C1，…Cs）|Fq為其子域子碼[N，K，d]，則，k≥sK-（s-1）N，d≥D.

通過有限域Fr上函數(shù)域碼V（G）來構(gòu)造廣義幾何碼C（P1，P2，…Ps；G；C1，…Cs），該廣義幾何碼具有非常的參數(shù)。在此基礎(chǔ)上，進(jìn)一步構(gòu)造廣義幾何碼的子域子碼，由定理3可以看出，其子域子碼有更好的參數(shù)。

[1]V D Goppa,Codes associated with divisors[J].Probl.Inform.Transm.1977,13:22-26.

[2]M A Tsfasman.S.G.Vlǎdut,and T.Zink.Modular curves,Shimura curves and Goppa codes,better than Varshamov-Gilbert bound.Math[J].Nachriechten,1982,109:21-28.

[3]H Niederreiter,C P Xing,and K Y Lam,A new construction of algebraic-geometry codes[J].Applicable Algebra Engineering.Comm.Comput,1999(9)373-381.

[4]Wanbao Hu,Zhen Wang,Improvements on the distance of onepoint codes using places of higher degree[J].Procedia Engineering，2011(15)：1711-1715.

[5]Chaoping Xing,Harald Niederriter,and Kwok Yan Lam,A Generalization of Algebraic Geometry Codes[J].IEEE transations on information theory,1999(7):1123-1127.

[6]H.Stichtenoth.Algebraic Function Fields and Codes[M].Berlin:Springer-Verlag,1993.

[7]Hachenberger D,Niederreiter H,Chaoping Xing Functionfield codes[J].Applicable Algebra in Engineering,Communication and Computing,2008,19(3):201-211.

[8]Chaoping Xing,San Ling,A class linear codes good parameters from algebraic curves[J].IEEE Inform Theory,2000,46(4):1527-1532.

[責(zé)任編輯：桂傳友]

O175

A

1674-1102(2014)06-0039-02

10.13420/j.cnki.jczu.2014.06.010

2014-07-23

池州學(xué)院研究生引進(jìn)啟動項目（2011RC035）。

王貞（1987-）,男，安徽東至人，池州學(xué)院數(shù)學(xué)與計算機(jī)科學(xué)系助教，碩士,研究方向為代數(shù)編碼。