非圓曲線參數(shù)自適應插補算法研究

曹智梅

（廣東松山職業(yè)技術學院，韶關 512126）

0 引言

對于數(shù)控系統(tǒng)來說，插補就是對曲線的起點、終點之間的空間進行數(shù)據(jù)密化，從而形成要求的輪廓軌跡的過程。插補是數(shù)控技術的核心，在插補過程中，密化的點如何選擇，按照什么規(guī)律進行計算，這就是插補算法要研究的核心問題。在數(shù)控加工中，常常遇到非圓曲線的加工，而一般的數(shù)控系統(tǒng)只配備了直線、圓弧等少數(shù)插補功能，因此給定曲線的理論軌跡不一定能直接處理，需要將給定的理論軌跡按允許的誤差進行離散逼近，生成一系列直線段（或圓弧段）所描述的刀具運動軌跡。

在采用直線逼近曲線的方式中，目前應用較廣的有等參數(shù)插補和等誤差插補，兩種插補方法各有優(yōu)缺點。等參數(shù)法計算簡單，但對于曲率變化較大的曲線會帶來插補誤差在局部超過允許誤差，從而降低加工的質量；等誤差法在控制插補誤差上具有較好的功能，但其節(jié)點的計算涉及到四次方程的求解，計算量大，使用受限。在目前流行的各種CAD/CAM軟件中，采取的方法是通過控制最小的加工誤差生成一系列的直線段，其程序的數(shù)量大，加工時間長，識別度差。

等參數(shù)插補方法在實際應用中還涉及到參數(shù)的選取問題，文獻[1]中分析了不同參變量（也就是等參數(shù)插補中的參數(shù)）對橢圓插補誤差的影響，這些分析說明選取的參變量不同，其插補產生誤差的大小和位置也不同，在同一位置采用不同參變量其誤差會有較大差異，這也給等參數(shù)插補的使用帶來了一定的限制。

本文在研究等參數(shù)插補算法的基礎上，提出一種新的參數(shù)自適應插補算法，并在橢圓曲線加工中進行了驗證。參數(shù)自適應插補算法是結合等參數(shù)插補的優(yōu)勢，借用等誤差逼近的原理，將等參數(shù)中的等參數(shù)設置成變參數(shù)，且能適用于不同的參數(shù)選取，通過參數(shù)增量的改變來實時調節(jié)插補的誤差，以確保插補誤差滿足允許條件。在保證加工質量的前提下，參數(shù)自適應插補比等參數(shù)插補算法的有更好的加工質量，比等誤差插補算法有更少的計算量。通過實例應用得出該方法既具有等參數(shù)插補計算簡單的優(yōu)點，又能兼顧到最大誤差的控制，具有良好的應用性和推廣性。

1 等參數(shù)直線插補誤差計算

1.1 等參數(shù)直線插補算法解析

非圓曲線的方程表示為 y = f(x)，當以自變量x作為參變量時，曲線按等參數(shù)Δx進行節(jié)點分割，即每兩個相鄰節(jié)點間的的參數(shù)差值均相同，如圖1所示，D點為曲線上一點，其坐標為（xi,yi），E點為變量增加了Δx后所對應的點，其坐標為（ xi+1,yi+1），DE之間通過直線插補，依次例推，完成了整個曲線的插補。

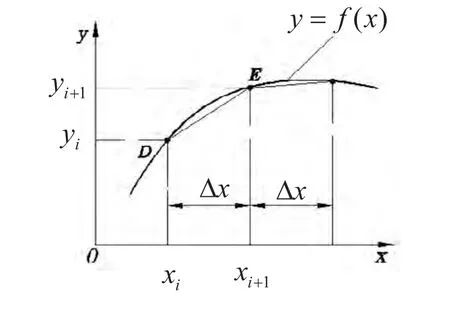
圖1 等參數(shù)插補示意圖

當曲線的方程不便直接表達時，可以轉化為參數(shù)方程表示：

對于參數(shù)方程，在等參數(shù)插補中，主要是保證相鄰兩點間的參數(shù)增量為一常數(shù)tΔ，當tΔ一定時，插補的節(jié)點可以直接計算得出。

等參數(shù)插補方法中只考慮了兩點間的參數(shù)增量，整個過程計算方便，但是對于各相鄰插補直線段的插補誤差卻并沒有考慮，一般情況下，為了保證插補誤差，只能是最大限度的減小參數(shù)增量，增加走刀的次數(shù)，對于曲率變化較大的曲線，等參數(shù)插補算法的應用受到了較大的限制。

1.2 直線插補誤差計算

要保證在插補過程中的計算方便，又要考慮到對最大插補誤差的控制。如果能將各直線段的插補誤差用公式算出，再對比插補誤差和允許誤差，當插補誤差大于允許誤差時，減少等參數(shù)插補中的參數(shù)增量，通過控制參數(shù)增量，達到控制插誤差的目的。

如圖2所示，即先在曲線 y = f(x)上取相鄰兩點D、E，兩點間的參數(shù)增量為Δx，D點對應的參數(shù)為 xi，函數(shù)值為 yi，E點對應的參數(shù)為 xi+1，函數(shù)值為 yi+1，則 xi+1=xi+Δx，接下來要計算直線DE的插補誤差。求解直線的插補的最大誤差，就是要在曲線 y = f(x)上要找到一條直線MN，此直線既與曲線相切于N點，又與直線DE平行，其切點N到直線DE的距離即是最大插補誤差。要計算距離，就先要計算切點N坐標，計算曲線時求出的點即為切點N。這種求解插補誤差的方法是比較準確，但是其切點N的坐標求解比較復雜的，特別是對某些導數(shù)不易求出的曲線更是比較難實現(xiàn)[2～5]。

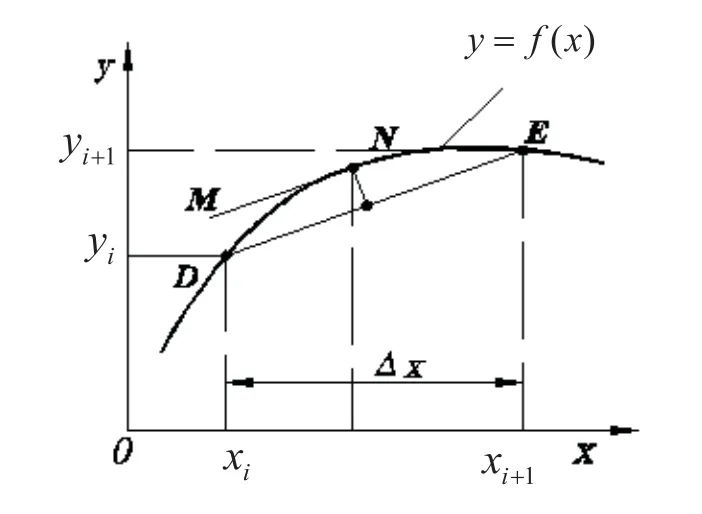
圖2 直線插補誤差計算示意圖

1.3 直線插補誤差近似計算

由于直線插補誤差算法比較復雜，在研究等參數(shù)插補算法的基礎上，引入中間參數(shù)點概念，用中間參數(shù)點來替代相切點，減少了對曲線求導的過程，用中間參數(shù)點到插補直線的距離近似作為插補誤差，這種方法大大減少計算量，同時對數(shù)值準確性的影響卻很小，有很好的適用性。如圖3所示，在 y = f(x)曲線上取兩點D、E，兩點間的參數(shù)增量為Δx，D點對應的參數(shù)為xi，函數(shù)值為 yi，E點對應的參數(shù)為 xi+1，函數(shù)值為 yi+1，在DE曲線段上上取一點F，使得將F點對應的參數(shù)為D、E這兩點參數(shù)的平均值，即點F對應的參數(shù)為通過參數(shù)可計算出中間參數(shù)點F的坐標，計算此時F點到直線DE的距離作為插補誤差。

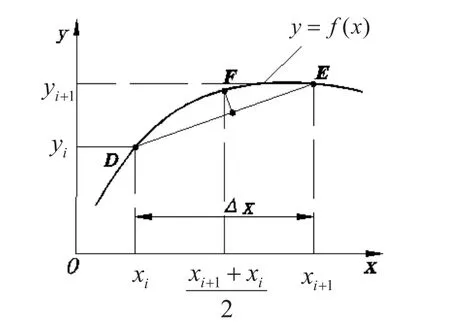
圖3 直線插補誤差近似計算示意圖

等參數(shù)直線插補誤差計算的過程中涉及到直線方程的表達，點到直線距離的計算。

2 點到直線的距離計算

2.1 過兩點的直線方程

如圖4所示，D、E為非圓曲線上的兩點，已知兩點的坐標為D(x1,y1)、E(x2,y2)，若x1=x2，則DE直線的方程可寫為x=x1，改為一般式為：

DE直線方程為y-y1=k(x-x1)，改寫成一般式為：

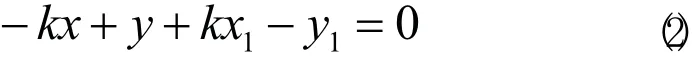
圖4 點到直線距離示意圖

2.2 點到直線的距離公式

直線的方程一般式為Ax+By+C=0，其中A、B、C為常數(shù)，且 A2+B2≠0，點F(x3,y3)到該方程的距離為：

將式（1）與直線方程的一般式進行對照，則此時 A=1,B=0,C=-x1。若要求點F( x3,y3)到DE連線的距離，則將此時的A、B、C的數(shù)值，F(xiàn)點的坐標代入式（3）可求出點F點到直線DE的距離為：

將式（2）與直線方程的一般式進行對照，則此時 A=-k,B=1,C=kx1-y1。若要求點F(x3,y3)到DE連線的距離，則將此時的A、B、C的數(shù)值、F點的坐標代入式（3）可求出點F點到直線DE的距離為：

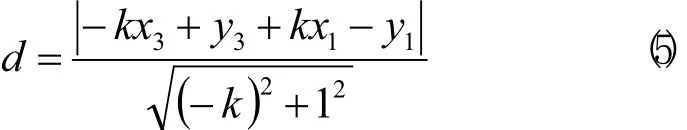
3 參數(shù)自適應插補算法

3.1 算法原理

在參數(shù)自適應算法中，一般曲線方程采用參數(shù)方程的形式。參數(shù)自適應算法的原理如下。

已知曲線的方程可表示為x=X(t)，y=Y(t)，參數(shù)的取值區(qū)間為[t1， tn]。先在已知曲線上取相鄰兩點D和E，D點對應的參數(shù)為ti，E點對應的參數(shù)為ti+1，設 ti+1=ti+Δt，設D點、E點的坐標為（xi,yi），（xi+1,yi+1），則有：

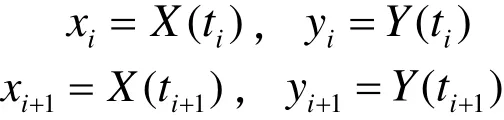
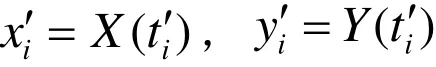
此時，F(xiàn)點到弦DE的距離d可通過式（5）進行求解（若xi=xi+1則用式（4）進行求解），將d也可看作直線插補的最大誤差。將求得的距離d與允許誤差d允進行比較，若此時d＞d允，則減少參數(shù)增量Δt；若此d≤d允，則DE兩點間直接插補滿足誤差條件，可以直接進行插補，如此例推，可以計算出所有的插補節(jié)點，完成整個曲線的加工。通過在加工過程中適時調整參數(shù)的增量Δt，使直線插補滿足誤差條件。

3.2 算法流程框圖

在進行自適應參數(shù)插補運算時，首先要給定一個刀具起點位置（參數(shù) t1所對應的位置），給定加工的允許插補誤差d允，設定一個合理的初始參數(shù)增量Δt，誤差Δt設置過大，增加了循環(huán)計算的次數(shù)，Δt設置過小則起不到減少走刀次數(shù)的作用。

在設計算法流程框圖時，有三個條件判斷。第一個條件判斷 ti≤tn是判斷是否已經插補到終點，如果到終點則結束程序，如果沒有到終點，則計算當前點D的坐標，下一插補點E的坐標，和參數(shù)中間點F的坐標。第二個條件判斷是判斷D點的橫坐標是否與E點的橫坐標相等，若xi=xi+1，則F點到直線DE的距離d =xi′-xi；若xi≠xi+1，則是比較距離d與允許誤差d允的大小，當d≤d允，走直線DE，當d＞d允時，減少插補的參數(shù)增量Δt，用新的Δt重新計算點的坐標，直至誤差滿足允許條件。走完這段直線DE后，將此時的終點所對的參數(shù)值賦值給下一個起點ti=ti+Δt，重新開始第一個條件判斷。圖5為參數(shù)自適應插補算法流程。

圖5 參數(shù)自適應插補算法流程圖

4 應用實例及分析

4.1 加工橢圓曲線

為了驗證參數(shù)自適應插補算法的正確性，現(xiàn)以加工橢圓曲線為例，其橢圓方程為y = 30sint，t的取值區(qū)間為[0，360]，采用參數(shù)方程進行加工，設加工的起點為（50，0），在等參數(shù)插補時，采用參數(shù)自適應插補算法時我們取Δt = 2，根據(jù)參數(shù)自適應算法，利用FAUNC機床自帶的循環(huán)語句[6]，編寫宏程序O0001。

O0001 程序名稱

#1=0給參變量t賦初值

#2=50橢圓的長半軸

#3=30橢圓的短半軸

#18=0.005設定允許插補誤差

S1500 M03主軸正轉

G54 G90 G40 G17設定加工坐標系

G00 X#2 Y0 Z50定位到起點

Z2 Z向快速定位

G1 Z-1 Z向下刀

WHILE [#1 LE 360] DO 1當參數(shù)t360≤時循環(huán)開始

#4=2給參數(shù)增量tΔ賦值

GOTO 2 跳轉到N2程序段

N1 #4=0.7*#4減少tΔ

N2 #14=#1+#4 計算下一點E的參數(shù)

#5=#2*COS[#1] 計算當前點D的x坐標

#6=#3*SIN[#1] 計算當前點D的y坐標

#7=#2*COS[#14] 計算下一點E的x坐標

#8=#3*SIN[#14] 計算下一點E的y坐標

IF[#5 EQ#7] GOTO 3 當D、E兩點的橫坐標相等時跳轉到N3程序段

#9=[#8-#6]/[#7-#5] 計算直線DE的斜率

#10=#1+0.5*#4 計算中間點F的參數(shù)

#11=#2*COS[#10] 計算中間點F的x坐標

#12=#3*SIN[#10] 計算中間點F的y坐標

#13=ABS[#12-

#9*#11+#9*#5-#6] 計算式（5）的分子

#15=SQRT[1+#9*#9] 計算式（5）的分母

#17=#13/#15 計算F到直線DE的距離d

GOTO 4 跳轉到N4程序段

N3 #17=ABS[#11-#5] 計算F到直線DE的距離d

N4 IF [#17 GT #18] GOTO 1當允d＞d時，跳轉到N1程序段

G01 X#7 Y#8 F500 走DE直線

#1=#1+#4 將此時終點的參數(shù)賦值給下一個起點的參數(shù)

END 1 循環(huán)結束

G1 Z5 抬刀

G0Z50 快速抬刀

G0X0 Y0 快速定位到XY的中心

M05 主軸停止

M30 程序結束

4.2 兩種插補算法對比分析

為了更好的對比等參數(shù)插補算法與參數(shù)自適應插補算法，對橢圓曲線進行加工。由于橢圓曲線為軸對稱圖形，僅對第一象限的四分之一的橢圓加工進行對比。其加工的四分之一橢圓尺寸如圖6所示，要求允許誤差為0.005。

圖6 加工的四分之一橢圓

對于圖6，如果采用等參數(shù)插補算法，取參數(shù)角t為參變量，t∈[0 , 90]，參數(shù)增量Δt為2，此時的走刀次數(shù)為45，再通過直線插補誤差算法可計算出此時的最大插補誤差和最小插補誤差分別為0.0076和0.0046。其插補誤差較均勻，但部分位置不滿足允許插補誤差，即不滿足質量要求。采用本文1.3所介紹的近似算法與1.2確準算法間的最大誤差為9. 9×10-15，說明其近似算法能完全滿足插補要求。取橫坐標x為參變量時，x∈[0 , 50]，此時對應于每一個x，有一個y對應，此時的走刀次數(shù)為50，再通過直線插補誤差公式可計算出此時的最大插補誤差和最小插補誤差分別為0.248和0.0015，其插補誤差不均勻，且部分位置不滿足允許插補誤差，即不滿足質量要求。等參數(shù)直線插補中，當插補誤差不滿足允許條件時，唯一的辦法只能是減少參數(shù)增量，當然此時走刀次數(shù)也會成倍的增加。

當采用參數(shù)自適應插補算法時，程序O0001是取參數(shù)角t為變量，初始參數(shù)增量Δt為2的參數(shù)自適應編程，此時的插補次數(shù)為63（可以通過在程序中設置計數(shù)變量得到），其最大插補誤差和最小插補誤差分別為0.005和0.0046，其插補誤差的變化幅度非常小，其加工曲線的誤差均勻，加工質量好。如果取橫坐標x為參變量，初始參數(shù)增量Δx = 1，此時的插補次數(shù)為65，其最大插補誤差和最小插補誤差分別0.005和0.0015。不管以參數(shù)角t還是橫坐標x作為參變數(shù)，采用參數(shù)自適應插補算法均能滿足插補誤差條件。

參數(shù)自適應插補算法與等參數(shù)插補算法結果對比見表1。從結果我們可以看出，參數(shù)自適應插補算法雖然走刀次數(shù)有所增加，但其計算簡單，加工誤差均勻，加工質量好，走刀次數(shù)不依賴于參數(shù)增量的大小，且參數(shù)變量的選擇對插補誤差的影響較小[7,8]。

5 結束語

本文在研究等參數(shù)插補的基礎上，提出參數(shù)自適應算法，主要研究工作有：

表1 兩種插補算法對比分析

1) 以參數(shù)中間點替代相切點來計算插補誤差，簡化的計算過程，且引起的誤差一般為10-10數(shù)量級甚至更小，對計算結果的影響可以忽略；

2) 在插補過程中，適時改變參數(shù)增量的大小，來控制插補誤差滿足許可條件；

3) 提出參數(shù)自適應直線插補算法，給出了算法的插補原理和算法流程圖；

4) 針對橢圓曲線的加工，將參數(shù)自適應插補和等參數(shù)插補方法進行對比，驗證算法的正確性和適用性。

[1] 陳小紅,姜曉強,曹秦崗.橢圓變量編程插補誤差分析與應用[J].機床與液壓,2012,40(16):59-63.

[2] 王愛群,李夢群,馮裕強.數(shù)控加工理論與實用技術[M].北京:機械工業(yè)出版社,2009,5

[3] 金艷玲,楊東武,姚東成.數(shù)控加工中非圓曲線輪廓的三圓弧逼近方法[J].組合機床與自動化加工技術,2013,(9):110-114.

[4] 文豪,高健.數(shù)控系統(tǒng)等誤差直線逼近節(jié)點算法分析與改進[J].機械設計與制造,2013,(9):217-219+223.

[5] 趙忠華,商瀟瀟.基于NURBS曲線的非圓曲線數(shù)控插補算法研究[J].機械工程與自動化,2013,(4):24-26.

[6] 陳海舟.數(shù)控銑削加工宏程序及應用實例（第二版）[M].北京:機械工業(yè)出版社,2007,12.

[7] 孫海洋,范大鵬,李玲.一種參數(shù)曲線實時數(shù)控插補計算新方法[J].國防科技大學學報,2008,30(3):59-63.

[8] 游有鵬,王珉,朱劍英.參數(shù)曲線的自適應插補算法[J].南京航空航天大學學報,2000,32(6):667-671.