無人值守傳感器網絡的高性能分布式存儲算法
肖宜龍, 蔣海波
(1. 中煤平朔集團有限公司,山西 朔州 036006; 2. 中國科學院 成都生物研究所,四川 成都 610041; 3. 中國科學院 成都計算機應用研究所,四川 成都 610041)
無人值守傳感器網絡[1-2]通常部署在惡劣環境中,數據收集節點Sink不固定在網絡中,而是每隔一段時間后在網絡中出現,收集各數據節點產生的數據包.在Sink節點出現之前,為避免數據包因節點損壞或是能量耗盡而丟失,各數據包通常分布式地存儲在整個網絡中.
筆者針對無人值守傳感器網絡的分布式存儲算法[3-5]進行研究.基本假設[6]為網絡由均勻分布的n個傳感器節點構成,其中k個為數據節點 (n>k),每個數據節點用來感知物理量并產生一個大小固定的數據包,稱為源數據包,其余的所有非數據節點只用來存儲數據.每個節點有相同的通信半徑,距離小于通信半徑的兩個節點互稱為鄰居節點,可以直接通信;處于通信半徑之外的節點通過多跳機制間接通信.網絡是連通的,但網絡中每一個節點都沒有路由表記錄如何與其通信半徑之外的節點間接通信,因此,兩個節點之間的間接通信是通過隨機選擇中間節點來完成的.
針對無人值守傳感器網絡設計的最新且最具代表性的分布式存儲算法是文獻[6]中提出的基于LT碼的算法.存儲過程中該算法采用簡單隨機游走規則將k個源數據包傳遞到網絡中的n個節點;每個節點按照LT碼的度分度函數接收一定數量的源數據包,并計算得到一個存儲數據包存儲起來.Sink節點出現后,通過訪問這些存儲數據包恢復出原來的源數據包.該方法主要有兩方面的缺點:一是簡單隨機游走的低效率以及算法本身的需求,導致每個源數據包為了遍歷網絡中所有的節點,在實際過程中至少需要傳遞 3nlnn次.因此,這增加了網絡的通信成本.二是Sink節點為了恢復出所有的k個源數據包,需要訪問k+kλ個存儲數據包 (λ> 0,與k的取值有關).文獻[6]的實驗表明k的數量級大于等于102時,kλ的值大于100.因此,這導致了Sink節點的訪問成本較高.針對LT碼算法的上述不足,尤其是考慮到如何降低網絡的通信成本(有利于傳感器網絡節能),筆者提出了一種基于源數據包傳遞過程中并行定向隨機游走規則和網絡中每個節點對源數據包獨立處理機制的分布式數據存儲算法.
1 并行定向隨機游走
為了用數值實驗模擬和驗證文中算法的有效性,將無人值守傳感器網絡抽象為一個連通的二維隨機圖[7].各傳感器節點用圖中的各頂點表示.若兩個傳感器節點互為鄰居節點,則用一條邊連接圖中對應的頂點;一個傳感器節點的數據包傳遞到另一個節點的過程用隨機幾何圖上一次隨機游走表示.
二維隨機圖上的隨機游走定義為按某一隨機序列訪問圖中頂點的過程.一次隨機游走開始于圖中某一頂點,并且下一步要訪問頂點是從當前訪問頂點的鄰居頂點中選取的;如果下一步要訪問的頂點是從當前訪問頂點的所有鄰居頂點中等概率隨機選取的,那么這樣的隨機游走稱為簡單隨機游走.
與文獻[6]中采用的簡單隨機游走規則不同,文中算法采用效率更高的并行定向隨機游走規則[8]在網絡中傳遞每個源數據包.下面先介紹(串行的)定向隨機游走規則,再介紹其并行化方式.
1.1 定向隨機游走規則
按照定向隨機游走規則,每當源數據包到達了當前訪問的傳感器節點v后,要從v的所有鄰居節點中選出一個作為下一步要訪問的節點u.
如果用N(o)表示任意一個節點o的鄰居節點集合,δ(o)表示節點o的鄰居節點個數,c(o)表示定向隨機游走目前已訪問節點o的次數,那么,下一步將要訪問的節點u的選取過程分為如下兩步:
步驟1 從當前訪問節點v的鄰居集合N(v)中隨機均勻地選擇2個節點作為備選節點.
步驟2 從2個備選節點(用集合N′表示)中選擇滿足下式的節點u作為下一步將要訪問的節點.
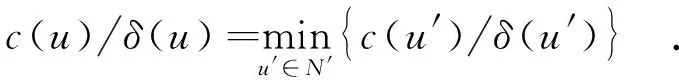
1.2 并行定向隨機游走規則
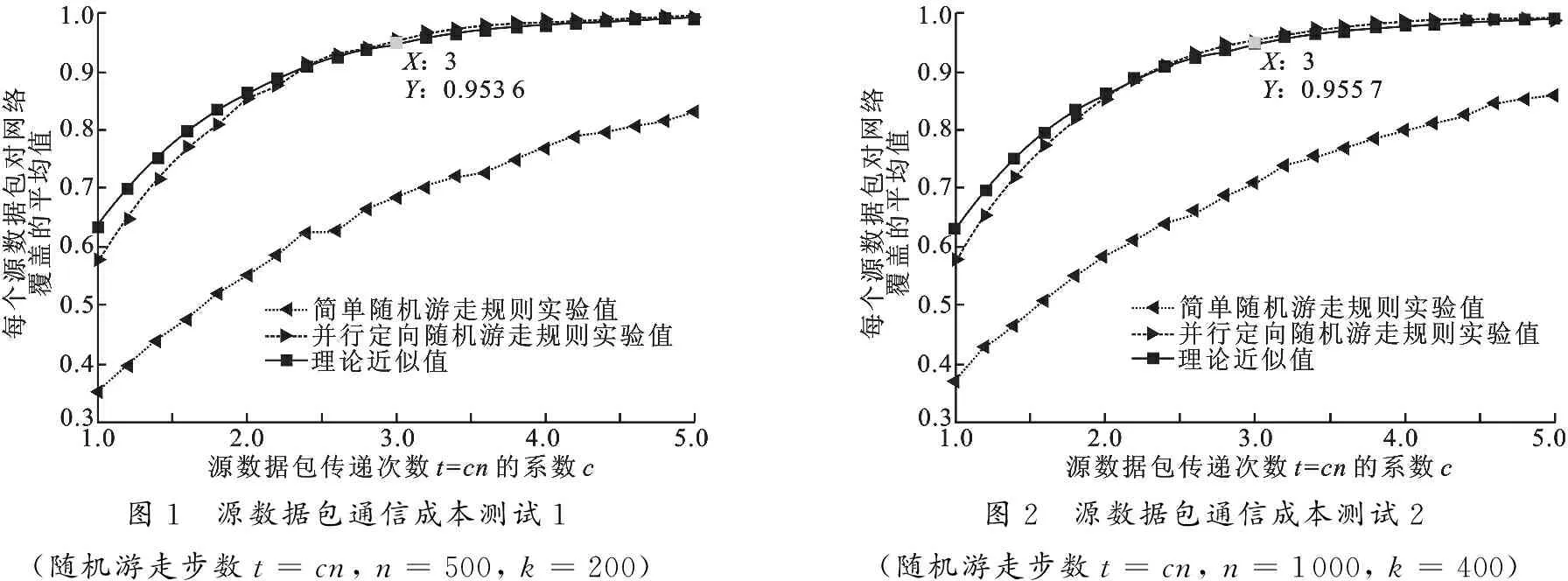
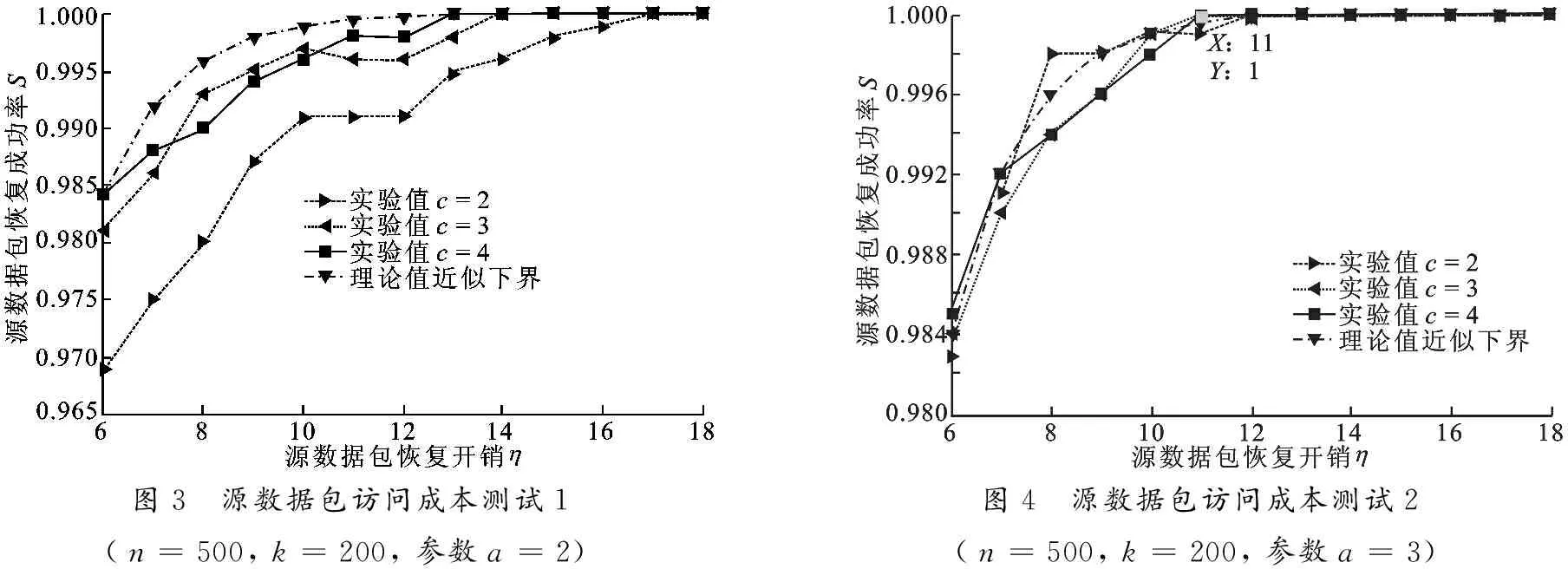
每個數據節點將其源數據包并行地向外發出m個副本(0 對于一個連通的二維隨機圖,用t表示隨機游走的步數,那么該隨機游走對圖的覆蓋率(也就是訪問到的不同頂點數占圖中總的頂點數的比例),其理論值可以近似地表示[9]為 1-exp(-t/n).因此,對于無人值守傳感器網絡,當采用隨機游走機制(串行或并行[10])傳遞每個源數據包時,理論上傳遞次數達到O(nlnn) 時,才能使得每個源數據包訪問到網絡中的每個節點. 文獻[6]提出的基于LT碼的方法,為使每個源數據包遍歷網絡中所有n個節點,每個源數據包的傳遞次數(文中將其看做網絡通信成本開銷)必須達到O(nlnn).為降低這一開銷,筆者提出了一種基于并行隨機游走機制的高性能分布式存儲算法,該算法只要求每個源數據包的傳遞次數達到O(n)即可. 文中算法的具體實現流程用代偽碼表示如下(命名為算法1): 算法1 無人值守傳感器網絡的高性能分布式存儲算法 輸入:k個源數據包Xv,v=1,…,k. 輸出:n個存儲數據包Yu,u=1,…,n. /*初始化階段*/ 1: For 每個數據節點v=1 tok 2: 為源數據包Xv添加頭信息: IDv號及定向隨機游走步數計數器N=0; 3: For 每個節點u=1 ton 4: 初始化每個存儲數據包的值:Yu=0; 5: 初始化每個源數據包Xv已訪問節點u的當前次數:cv(u)=1,v=1,…,k;/*分布式存儲階段*/ 6: For 每個數據節點v=1 tok 7: 按照概率alnk/k接收Xv,并且更新自己的存儲數據包:Yv=Yv?Xv; 8: 按照定向隨機游走規則將源數據包Xv的m個副本分別傳遞出去; 9:cv(v)=cv(v)+1; 10: For 每個節點u=1 ton 11: For 每個到達節點u的源數據包Xj 12: IfXj是第一次訪問節點u 13: 節點u按照概率alnk/k接收Xj,并且更新自己的存儲數據包:Yu=Yu?Xj; 14:cj(u)=cj(u)+1; 15: 源數據包Xj更新頭信息:N=N+1; 16: IfN 17: 節點u按照定向隨機游走規則將源數據包Xj傳遞到它的一個鄰居節點; 18: Else 19: 節點u丟棄Xj; 算法結束. 算法1完成之后,每個節點存儲了一個存儲數據包,源數據包不再存儲.算法有兩個重要參數: 一個是定向隨機游走步數,即每個源數據包副本的傳遞次數,設置為cn/m,用變量N來計數;副本每傳遞一次N的值加1,當N>cn/m時,副本被丟棄,不再傳遞.另一個參數是每個節點接收一個新到達的源數據包副本的概率,算法中設置為alnk/k.算法性能主要由這兩個參數決定.下面做具體分析. 當算法1執行完成之后,k個源數據包被分布式地存儲到網絡的n個節點中,每個節點存儲的存儲數據包都是若干個源數據包的異或和(每個源數據包和存儲數據包都看做是二元域上的比特向量).下文將分析Sink節點收集到多少個存儲數據包之后可以恢復原來的k個源數據包. 假定Sink節點出現后,隨機地從k+ε個未損壞節點中收集了k+ε個存儲數據包.為便于描述,這k+ε個存儲數據包表示為Yi,i=1, 2, …,k+ε.每個存儲數據包都是源數據包的線性組合,因此,任意一個Yi,i=1, 2, …,k+ε,都可以表示為下式(式中的乘法為二元域上的元素與二元域上的向量之間的數乘): Yi=gi·[X1,X2,…,Xk]T, (1) 其中,X1, …,Xk表示k個未知的源數據包,gi是一個獨立的且取值在二元域上的隨機行向量,稱為存儲數據包Yi的生成行向量.當gi的某個元素gij取值為1時表示對應的源數據包Xi被接收.假定步數為t=cn的并行定向隨機游走覆蓋的各節點均勻地分布在網絡中,那么,由算法1可知:gi中每個元素gij,j=1,…,k,都是獨立取值的,且都服從式(2)定義的分布. (2) 這k+ε個存儲數據包的生成行向量構成了一個(k+ε)×k階矩陣G(k+ε)×k,稱為這k+ε個存儲數據包的生成矩陣,即G(k+ε)×k= [g1,g2, …,gk+ε]T.借助生成矩陣,這k+ε個存儲數據包可以表示為 [Y1,Y2,…,Yk+ε]T=G(k+ε)×k·[X1,…,Xk]T. (3) 若生成矩陣G(k+ε)×k存在一個可逆k×k階子矩陣,也就是G列滿秩,則式(3)定義的方程組存在惟一一組解,解方程組后可求得k個未知的源數據包X1, …,Xk.因此,Sink節點可由任意k+ε個存儲數據包計算得到k個未知源數據包的概率等于這k+ε個存儲數據包的生成矩陣G(k+ε)×k列滿秩的概率.如果用Pfailure表示二元域上的生成矩陣G(k+ε)×k列不滿秩的概率,當式(2)成立時,得到如下結論: 引理1 當G(k+ε)×k的每個元素的取值服從式(2)定義的分布時,Pfailure的上界為 (4) 證明 若G(k+ε)×k的各列線性相關,則G(k+ε)×k列不滿秩,因此 (5) 令R表示G(k+ε)×k的任意一個行向量,用w表示向量x中1的個數,因為行向量R的每一個元素取值獨立,且取值為1的概率由式(2)定義,因此 (6) 因為矩陣G(k+ε)×k的每一個行向量獨立,因此,G(k+ε)×kxT=0的概率為 (7) 當向量x取所有不同的值時,根據式(5)可得到引理1中的結論. 綜合上述分析,可用如下定理1描述算法1的性能. 定理1 采用算法1,Sink節點可由隨機選取的k+ε個存儲數據包計算得到原來的k個源數據包的概率Psuccess滿足: (8) 另外,通過數值實驗發現(鑒于篇幅關系,這里不再列出相關實驗結果),當式(8)中的參數(1-exp(-c))a≥2 時,Psuccess的下界主要由ε的值決定,可以用簡化表達式 1-(1/2)ε近似表示Psuccess的下界. 算法的數值實驗在MATLAB環境下進行.用隨機生成的二維隨機圖模擬網絡,在L×L= 100×100的正方形區域隨機均勻地分布n個點模擬傳感器網絡各個節點,其中數據節點的比例設置為40%,即k=0.4n,每個節點的通信半徑R滿足R2= (2 lnn/(πn))L2(按照隨機幾何圖的理論,這一條件保證了網絡極大的連通概率).實驗分為兩組,第1組測試網絡的通信成本,即存儲過程中每個源數據包在達到一定的網絡覆蓋率前提下需要在網絡中的傳遞次數.通信成本越低,越有利于節約網絡中各節點的通信能耗.第2組測試讀取源數據包時的訪問成本,即存儲完成之后,Sink節點需要訪問多少個存儲數據包才能恢復出原來的k個源數據包.訪問成本越低,允許損壞的傳感器節點就越多,網絡的可靠性就越高. 每個源數據包都按照并行隨機游走機制在網絡中傳遞,每個源數據包并行傳遞的副本數設為m=2,當m個副本總的傳遞次數,即隨機游走的總步數為t時,網絡覆蓋率的理論值[9]近似為 1-exp(-t/n).實驗中將并行定向隨機游走的總步數設為t=cn時,單個副本的傳遞次數設置為cn/m.實驗測試了k個源數據包對網絡各節點的平均覆蓋率與系數c之間的關系.作為對比,也測試了采用簡單隨機游走機制時的相關性能.圖1、圖2所示為n,k,c取不同值時的實驗結果. 圖1 源數據包通信成本測試1(隨機游走步數t=cn, n=500, k=200)圖2 源數據包通信成本測試2(隨機游走步數t=cn, n=1000, k=400) 從圖1和圖2中可以看出,采用并行定向隨機游走機制,k個源數據包對網絡覆蓋率平均值的實驗值與理論值 1-exp(-t/n) 是近似相等的.當t=n時,實驗值接近60%,當t=3n時,基本上每個源數據包都能覆蓋網絡中超過95%的節點.而采用簡單隨機游走規則,實驗值明顯小于理論值,比并行隨機游走機制的網絡覆蓋率平均低約20%.因此,采用定向隨機游走機制能有效降低網絡的通信成本.同時,采用并行定向隨機游走機制時,網絡中每一時刻平均有mk個源數據包被同時處理,提高了網絡的吞吐率,節省了整個存儲過程的耗時;而采用簡單隨機游走機制時,網絡中每一時刻只有k個源數據包處理. 需要說明的是,當每個源數據包并行傳遞的副本數m小于lnn值時,實驗結果與圖1和圖2所示類似;而當m大于 lnn值時,網絡覆蓋率隨m的增大而減小. 測試存儲過程完成之后,Sink節點為得到k個源數據包而訪問的存儲數據包的個數.實驗結果用如下兩個變量之間的關系描述:源數據包恢復開銷η,即Sink節點訪問到的存儲數據包個數h與源數據包個數k之差;源數據包恢復成功率S,即Sink節點能從h個存儲數據包計算出k個源數據包的概率. 實驗中主要調節參數為每個源數據包的并行定向隨機游走的總步數cn的系數c以及每個傳感器節點接收一個新到達的源數據包的概率alnk/k的系數a.圖3至圖6所示為不同網絡規模下,c和a的取值不同時,S與η之間的關系(圖中S的每個值都是 1 000 次實驗的平均值). 從圖3至圖6可以看出, 當參數a≥2時, 只要c的取值增大, 就能以較少的源數據包恢復開銷成功計算出原來的源數據包.進一步地,從圖4、圖6可以看出,當參數a=3 時,只要c≥3,Sink節點就能從任意收集到的k+11 個以上的存儲數據包以100%的概率恢復出k個源數據包.此時,式(8)中的 (1-exp(-c))a≥ (1-exp(-3)) 3≈ 2.85.按定理1的結論,當η≥11 時,理論上Sink節點可由任意k+η個存儲數據包計算得到原來的k個源數據包的概率S近似大于 1-2-11≈ 99.95%,實驗值基本上驗證了理論值. 圖3 源數據包訪問成本測試1(n=500, k=200, 參數a=2)圖4 源數據包訪問成本測試2(n=500, k=200, 參數a=3) 圖5 源數據包訪問成本測試3(n=1000, k=400, 參數a=2)圖6 源數據包訪問成本測試4(n=1000, k=400, 參數a=3) 鑒于篇幅有限,參數a和c取其他值時的實驗結果不在文中列出.不過筆者發現,當 (1-exp(-c))a小于2時,實驗結果不穩定;當 (1-exp(-c))a取值不是很大時,實驗結果與 (1-exp(-c)) 3 時的類似;而當 (1-exp(-c))a取值較大時,反而會使得成功恢復源數據包的概率降低.因此,建議在實際應用中,取a=3,c=3 即可,這樣既能獲得好的穩定性,也能使網絡各節點的計算成本較低(因為a的值越大,每個節點接收源數據包的概率就越大,因而計算成本就會提高). 文獻[6]提出的基于LT碼的算法中,單個源數據包在網絡中總的傳遞次數為O(nlnn),并指出這一值達到 3nlnn時實驗效果較好.而文中方法所需傳遞次數為O(n),實驗中將這一值設置為3n時就能得到很好的源數據包恢復性能.另外,采用基于LT碼的算法,Sink節點為了恢復出k個源數據包而需要訪問的存儲數據包的個數與LT碼的譯碼性能有關.文獻[6]的實驗表明,當k大于100時,只有當源數據包恢復開銷η的值較大(大于100)時,Sink節點才能成功恢復出源數據包.而采用文中方法,不論k的取值如何,成功恢復k個源數據包,Sink節點只需訪問k+11 個存儲數包.對于某些實驗參數,文中算法(源數據包傳遞次數設置為3n,參數a的值設置為3)與基于LT碼算法(源數據包傳遞次數設置為 3nlnn,譯碼時采用極大似然譯碼算法)的具體對比結果列于表1中. 綜上可得出結論: 采用文中算法可以有效節約存儲過程中的通信成本和Sink節點的訪問成本. 表1 性能比較 筆者研究了無人值守傳感器網絡的高可靠性數據存儲問題,依靠源數據包傳遞過程中的并行定向隨機游走機制和網絡中每個節點對源數據包的獨立處理機制,提出了一種執行簡單,性能高效的分布式數據存儲算法.與同類方法相比,文中方法能有效降低存儲過程中各節點的通信成本和Sink節點的訪問成本. [1] Reddy S K V L, Ruj S, Nayak A. Distributed Data Survivability Schemes in Mobile Unattended Wireless Sensor Networks [C]//Proceedings of IEEE GLOBECOM. Piscataway: IEEE, 2012: 979-984. [2] 郭江鴻, 馬建峰, 張留美, 等. 高效的無線傳感器網絡加密數據匯聚方案 [J]. 西安電子科技大學學報, 2013, 40(3): 95-101. Guo Jianghong, Ma Jianfeng, Zhang Liumei, et al. Efficient Encrypted Data Aggregation Scheme for Wireless Sensor Networks [J]. Journal of Xidian University, 2013, 40(3): 95-101. [3] Mitra S, De Sarkar A, Ray S. A Review of Fault Management System in Wireless Sensor Network [C]//Proceedings of the CUBE International Conference on Information Technology. New York: ACM, 2012: 144-148. [4] Vitali D, Spognardi A, Mancini L V. Replication Schemes in Unattended Wireless Sensor Networks [C]//Proceedings of 4th IFIP International Conference on New Technologies, Mobility and Security. Piscataway: IEEE, 2011: 1-5. [5] 任偉, 任毅, 張慧, 等. 無人值守無線傳感器網絡中一種安全高效的數據存活策略 [J]. 計算機研究與發展, 2009, 46(12): 2093-2100. Ren Wei, Ren Yi, Zhang Hui, et al. A Secure and Efficient Data Survival Strategy in Unattended Wireless Sensor Network [J]. Journal of Computer Research and Development, 2009, 46(12): 2093-2100. [6] Kong Z, Aly S A, Soljanin E. Decentralized Coding Algorithms for Distributed Storage in Wireless Sensor Networks [J]. IEEE Journal on Selected Areas in Communications, 2010, 28(2): 261-267. [7] Cooper C, Frieze A. The Cover Time of Random Geometric Graphs [J]. Random Structures and Algorithms, 2011, 38(3): 324-349. [8] Avin C, Krishnamachari B. The Power of Choice in Random Walks: An Empirical Study [J]. Computer Networks, 2008, 52(1): 44-60. [9] Tzevelekas L, Oikonomou K, Stavrakakis I. Random Walk with Jumps in Large-scale Random Geometric Graphs [J]. Computer Communications, 2010, 33(13): 1505-1514. [10] Cooper C, Frieze A, Radzik T. Multiple Random Walks in Random Regular Graphs [J]. SIAM Journal on Discrete Mathematics, 2009, 23(4): 1738-1761.2 高性能分布式數據存儲算法
2.1 算法流程
2.2 算法性能分析
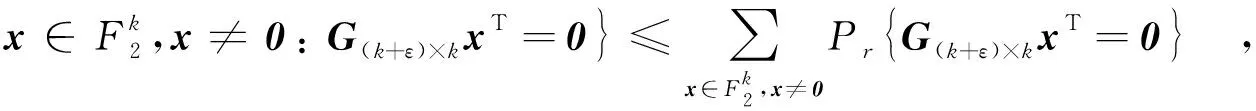
3 數值實驗
3.1 存儲源數據包的通信成本實驗
3.2 讀取源數據包的訪問成本實驗

3.3 性能比較

4 結 束 語

