給定邊界面積最小的曲面的平均曲率為零的證明方法

邢家省，賀慧霞，高建全

（1.北京航空航天大學數(shù)學與系統(tǒng)科學學院，北京100191；2.數(shù)學、信息與行為教育部重點實驗室，北京100191；3.平頂山教育學院，河南平頂山467000）

給定邊界面積最小的曲面的平均曲率為零的證明方法

邢家省1，2，賀慧霞1，2，高建全3

（1.北京航空航天大學數(shù)學與系統(tǒng)科學學院，北京100191；2.數(shù)學、信息與行為教育部重點實驗室，北京100191；3.平頂山教育學院，河南平頂山467000）

在曲面論幾何中，定義平均曲率為零的曲面為極小曲面。而在三維歐氏空間中，給定邊界的閉曲面中面積最小的曲面，其平均曲率一定為零，即給定邊界的閉曲面中面積最小的曲面為極小曲面。文章用變分理論給出幾種新的證明，使證明過程更加直接明了。

極小曲面；正則曲面；平均曲率；變分方法

引言

以空間封閉曲線Γ為邊界的曲面中，尋找其面積最小者，這樣的問題稱為極小曲面問題［1_10］。這涉及到面積最小曲面的存在性、唯一性等問題，人們通過考察面積最小曲面的必要條件，試圖尋找到面積最小的曲面［1_10］。現(xiàn)已證明，在固定邊界的曲面族中，假若存在面積最小的曲面，則面積最小的曲面的平均曲率為零［1_11］。這個結(jié)果已被人們用多種方式給予了證明，文獻［1_9］中給出的原始傳統(tǒng)證明過于繁瑣，有些證明過程也不太全面。本文在文獻［1_9］的基礎上，給出幾種完備的證明過程，便于人們查找確認使用。

1 參數(shù)分量表示的面積最小的曲面的平均曲率為零的證明

設Γ是一封閉空間光滑曲線，∑是過Γ的一曲面，且以Γ為邊界。

設正則曲面∑的參數(shù)表示為：

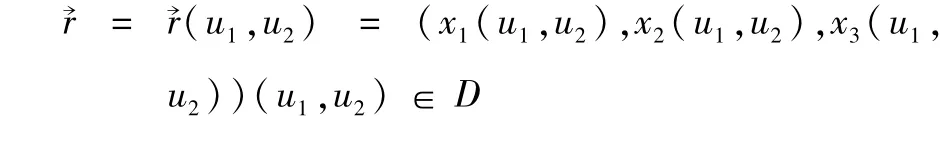
記

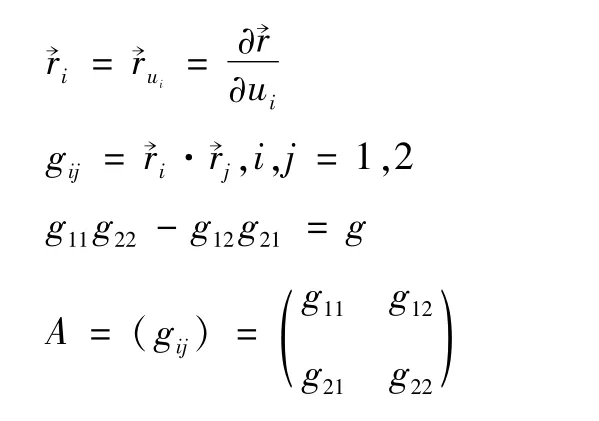
命

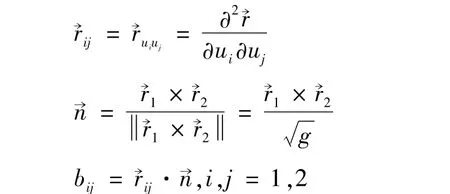
曲面的平均曲率［1_6，12_13］：

曲面∑的面積為：

其中

過曲線Γ的曲面∑滿足什么條件，使I取到局部極小值。

假若泛函I在某處達到最小值，考查其必要條件。

由變分引理，設D為R2中的開集，f∈C（D），若對任意，都有，則必有f（u， ）=0，（u， ）∈D。

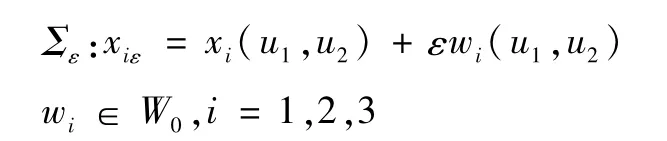
則曲面∑ε的面積為

顯然，若I在（x1，x2，x3）處達到最小值，則對任意wi∈W0，i=1，2，3。

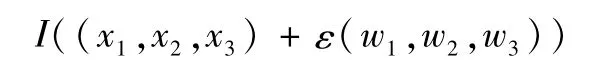
在ε=0處達到最小值，所以

經(jīng)計算，得

利用格林公式，得

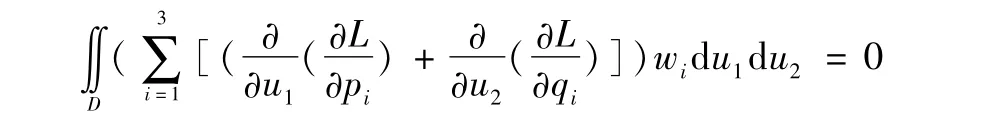
對任意wi∈W0，i=1，2，3。于是

由于

從而

利用恒等式［2］

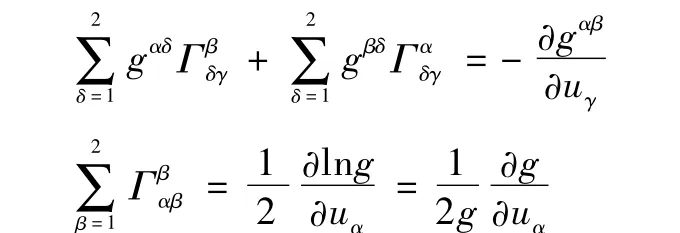
得

利用曲面論中的基本公式［1_6］

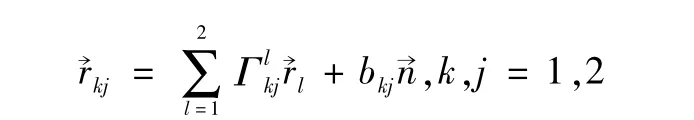
得

其中→n=（n1，n2，n3）是曲面上的單位法向量。于是

而

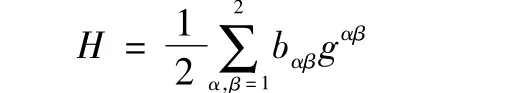
所以有

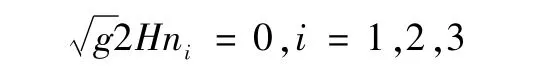
從而H=0。

定理1對于過空間光滑閉曲線Γ的曲面∑，如果Γ所圍的曲面∑的面積最小，則曲面∑的平均曲率恒等于零。

平均曲率為零的曲面，未必是面積最小的曲面。

2 向量表示的面積最小的曲面的平均曲率為零的證明

設Γ是一封閉空間光滑曲線，∑是過Γ的一曲面，且以Γ為邊界。

設正則曲面∑的向量參數(shù)表示為→r=→r（u， ），（u， ）∈D。則曲面∑的面積為

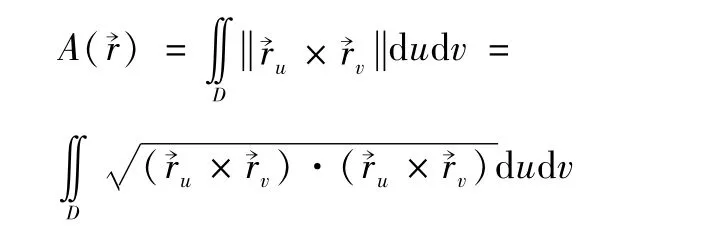
記

考慮擾動曲面［9］

其中ε∈（-δ，δ），δ＞0充分小，曲面∑ε以Γ為邊界，其面積為

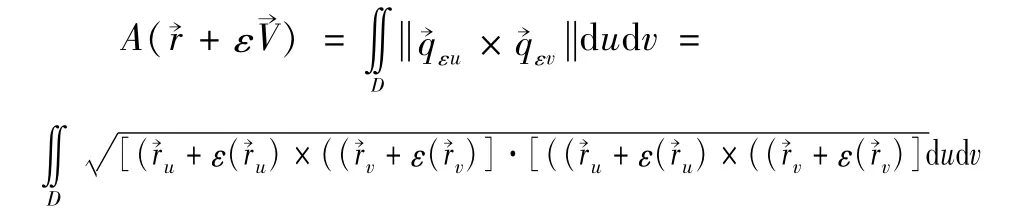
若∑是面積最小的曲面，則有

經(jīng)計算，可知

其中→ν為區(qū)域D的邊界?D上的單位外法向量，從而

由于→nu=-a→ru-b→r，→n=-c→ru-d→r，曲面的平均曲率

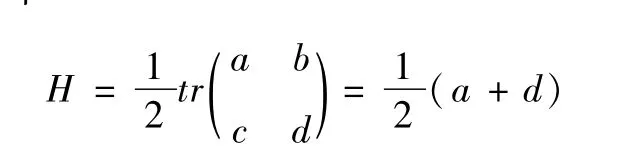
所以

于是

故有

由→ ∈W0的任意性，得

故對面積達到最小的曲面有H=0。

3 法向量擾動曲面中面積最小的曲面的平均曲率為零的證明

設Γ是一封閉空間光滑曲線，∑是過Γ的一曲面，且以Γ為邊界。

設正則曲面∑的參數(shù)表示為

則曲面∑的面積為

記W0=｛f（u， ）：f（u， ）∈C20（D）｝，令→ρ=f（u， ）→n，→n是曲面∑上的單位法向量，考慮法向擾動曲面［3，5，6］

其中ε∈（-δ，δ），δ＞0充分小；曲面∑ε以Γ為邊界，其面積為：

若∑是面積最小的曲面，則有

易知

將

代入，得

由于

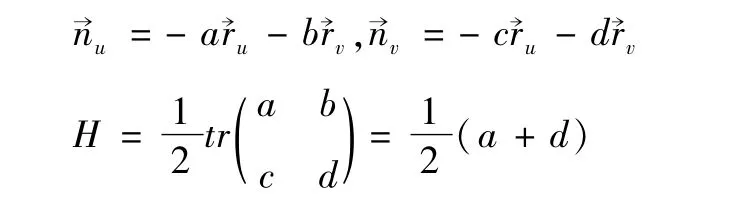
所以

或者利用Lagrange恒等式

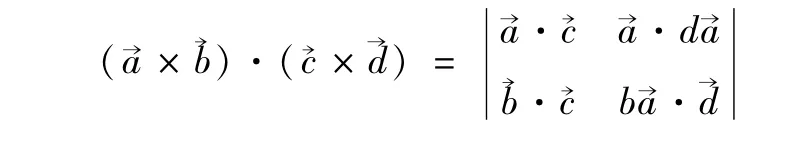
得到

于是

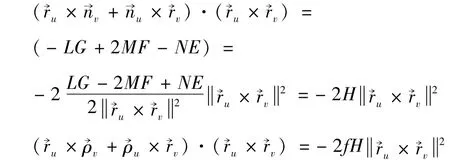
所以

從而

由f∈W0的任意性，得H，故對面積達到最小的曲面有H=0。

對顯式表示的曲面z=f（x，y），（x，y）∈D，關于固定邊界面積最小的曲面的性質(zhì)研究可見文獻［3_4，7，9］。

［1]梅向明，黃敬之.微分幾何［M].4版.北京:高等教育出版社，2008.

［2]陳維桓.微分幾何［M].北京:北京大學出版社，2006.

［3]彭家貴，陳卿.微分幾何［M].北京:高等教育出版社，2002.

［4]馬力.簡明微分幾何［M].北京:清華大學出版社，2004.

［5]王幼寧，劉繼志.微分幾何講義［M].北京:北京師范大學出版社，2003.

［6]蘇步青，胡和生，沈純理，等.微分幾何［M].北京:人民教育出版社，1980.

［7]陳維桓.極小曲面［M].大連:大連理工大學出版社，2011.

［8]澤維爾，潮小李.現(xiàn)代極小曲面講義［M].北京:高等教育出版社，2011.

［9]John OPrea.微分幾何及其應用［M].陳智奇，李君，譯.北京：機械工業(yè)出版社，2006.

［10]彭家貴，童占業(yè).極小曲面中的若干問題［J].數(shù)學進展，1995，24（1）：1_27.

［11]陳欣高.利用科達齊一邁因納爾迪公式推導極小曲面的幾個性質(zhì)和性質(zhì)的應用［J].河南師范大學學報，19S5（3）：100_107.

［12]邢家省，王擁軍.曲面上法曲率的最值和最值切方向的性質(zhì)［J].吉首大學學報：自然科學版，2013，34（1）：6_10.

［13]邢家省.法曲率最值的直接求法［J].吉首大學學報：自然科學版，2012，33（4）：11_15.

New Ways to Prove the Mean Curvature（H≡0）of the Minimal Surfaces Under Prescribed Boundary Condition

XING Jiasheng1，2，HE Huixia1，2，GAO Jianquan3
（1.School of Mathematics and Systems Science，Beihang University，Beijing 100191，China；2.LMIB of the Ministry of Education，Beijing 100191，China；3.Pingdingshan Institute of Education，Pingdingshan 467000，China）

In surface theory，theminimal surfaces are the surfaceswithmean curvatures H=0.It's alsowell known that mean curvatures of the closed surfaceswith minimal area under Prescribed boundary must be zero，itmeans that the closed surfaceswithminimal area under Prescribed boundary areminimal surfaces.By using the variation theory，several new meth_ ods to Prove this conclusion are given.These new waysmake the Process of Proofmore directly and clear.

minimal surface；regular surface；mean curvature；variation method

O1S6.1

A

1673_1549(2014)02_0083_05

10.11863/j.suse.2014.02.18

2013_11_23

國家自然科學基金資助項目（11171013）

邢家省（1964_），男，河南泌陽人，副教授，博士，主要從事偏微分方程、微分幾何方面的研究，（E_mail）xjsh@buaa.edu.cn