局部氣墊雙體船波浪譜反演方法研究

徐登輝 鄒 勁

（哈爾濱工程大學 多體船技術國防重點學科實驗室 哈爾濱150001）

局部氣墊雙體船波浪譜反演方法研究

徐登輝 鄒 勁

（哈爾濱工程大學 多體船技術國防重點學科實驗室 哈爾濱150001）

為了使局部氣墊雙體船在航行過程中能時刻感知海況來調節氣墊氣流量，分析對比了從海浪波高信號反推出海浪譜的4種方法，從而為選取出氣墊控制系統內反演波浪譜提供最優控制算法。通過已知海浪譜的波浪，將反演出的海浪譜與已知譜對比，尋找出最優算法。最終表明Welch法的結果較理想，可達到工程應用精度。

譜分析；ITTC譜；局部氣墊雙體船；Welch法

引 言

局部雙體氣墊船作為一種較新穎的船型，國內研究尚處于起步階段，相關配套設施研究較少。局部氣墊雙體船氣墊控制系統作為氣墊船的核心部件，對船的阻力性能、耐波性能、物理場等有著決定性的影響，是該船達到戰略目標及預期航行性能的關鍵所在。氣墊控制系統的技術難點在于局部氣墊雙體船需根據船體航行姿態，時時調節氣墊氣流量，以達到各種航速、載重量和海況下的最優流量，從而實現船體航行性能的優化；而從船體姿態傳感器所獲得的信號，通過數字信號處理來求解當時航行海域的波高，則是關鍵［1］。本文通過應用ITTC譜制造出波浪，而后應用四種譜分析法再反演出波浪譜，最后將結果與造波的ITTC譜對比，從而找尋出最優譜分析法。該方法為后續波浪譜預報海況奠定基礎。

1 由氣墊船運動反推海況過程介紹

局部氣墊雙體船由于船型的創新，國內相關理論研究較少，本文針對工程上對局部氣墊雙體船控制系統在控制流量時需判斷海況的要求，研究其中影響海況反演結果較大的波浪譜分析法。由于船有縱傾角及橫傾角，限于篇幅，這里僅針對縱傾角譜分析法作相關探索研究。

圖1～圖3為氣墊船從三維模型到船模實驗及中試艇實驗的相關實驗圖片，船模及中試艇在各海況的航行試驗及相關實驗數據為海浪譜分析的過程提供有利的驗證手段。

圖1 局部氣墊雙體船三維模型

圖2 局部氣墊雙體船船模

圖3 局部氣墊船體船中試艇實驗

氣墊船控制系統的控制過程如圖4所示。

在上述過程中，誤差主要來源于通過運動信號判斷海況，從而構成了氣流量控制系統的研究核心。

該過程中，針對縱傾角信號，可用圖5所示流程來實現。

由于某些實驗因素，導致誤差只能控制在一定范圍，因此提高精度的重點就放在了對縱傾角進行譜分析上。為了有效選取高精度、高穩定性的譜分析法，以下介紹了四種常用的用于數字信號處理的譜分析法。選取最優譜分析法的過程圖6所示。

圖4 氣墊船控制系統原理

圖5 由運動信號判斷海況分析過程

圖6 譜分析法選取過程

通過以上步驟，就能選取出最優譜分析法，并將該算法應用于局部氣墊雙體船的控制系統。

2 ITTC譜造波及四種譜分析法介紹

2.1 ITTC譜造波

制造波浪過程中應用國際船模試驗池會議推薦的標準海浪譜(簡稱ITTC波譜）［1］

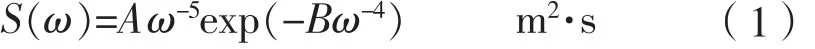
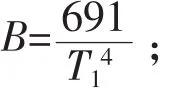
H1/3為不規則波有義波高，m；

T1為波浪特征周期，s。

根據設置風速，就可以給出具體海浪譜。通過海浪譜造波模擬海浪，主要有兩種途徑：線性疊加法和有理譜法。前者根據對海浪譜分割法的不同分為：頻率等分法和能量等分法。

本文采用頻率等分法來造波，具體方法如下：

根據海浪理論，長峰不規則波浪可以由許多不同頻率、幅值和隨機相位的諧波疊加而成［2］，可表示為：

εi為初相位， εi∶（0，2π）均勻分布；

ζai，ki是第i個組成波的振幅和波數，

式中：ωi為各波浪圓頻率，rad/s。

振幅可以由選定的輸入海浪譜S（ω）確定。

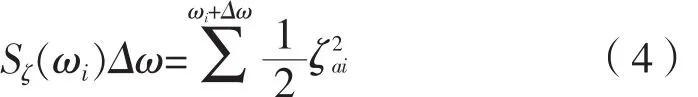
因此，第i個子波的振幅：

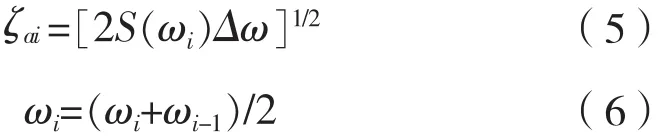
長峰不規則波浪的實現可表示為：

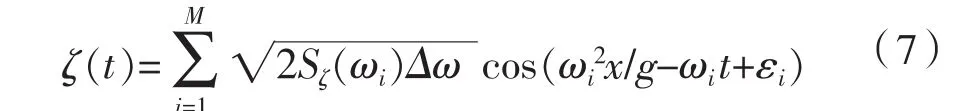
此式描述了輸入海浪譜與波浪時間序列的聯系。由上式，就可以根據已知理論波浪譜，將其分割成M段，從而確定各段諧波內振幅和初相角，再將其疊加，就得到長峰不規則波。

根據線性海浪理論，線性模擬結果反映了線性隨機海浪外觀上和統計上的特征，即波面位移表現為上下對稱、均值為零，其正態性偏度和峰度應為0和3。

2.2 波浪信號采樣

在已知仿真海浪波高坐標的情況下，對確定性時間序列進行功率譜或能譜分析，通過從時域到頻域的轉換，簡化后續信號傳遞過程的計算。設有一組確定性時間序列x0，x1，x2，…xN-1（N是正整數），采樣頻率為：

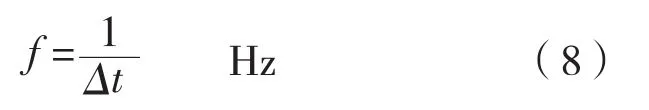
香農采樣定理：對于一個有限帶寬的模擬信號xa(t)，其頻譜的最高頻率為fmax，對xa(t)采樣時，若保證采樣頻率［2］：那么，可由采樣信號xa(nTs)完全恢復出原始的模擬信號，即xa(nTs)保留了xa(t)的全部信息。

對于波浪頻率，結合氣墊船響應頻率，可以判定：采樣頻率取2 Hz，采樣時間間隔為0.5 s，能保留中低頻波浪信息。采樣點數N=256，即256 s更新一次。由此，可對模擬波浪每隔0.5 s采樣一次，并應用下面所述方法進行波浪譜反演。

2.3 四種譜分析法介紹

2.3.1 直接法［3］

計算步驟如下：

第一步：計算F(ω，T)或F(ω)，兩者的離散形式為：

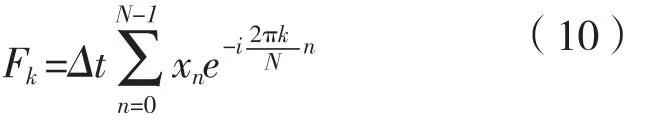
第二步：如果總能量無限，則需要計算功率譜密度。根據功率譜密度S(ω)的定義

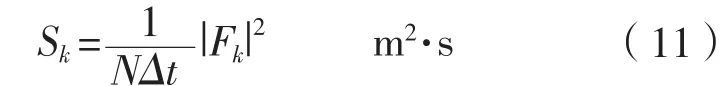
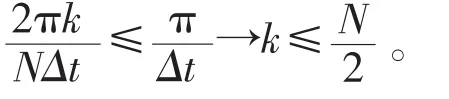
2.3.2 間接法［1］

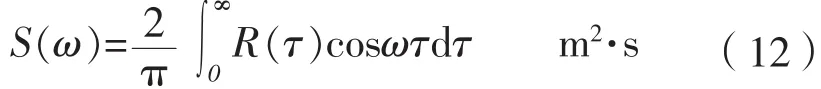
其中，自相關函數 往往使用有偏估計式：

針對海浪譜步驟如下：

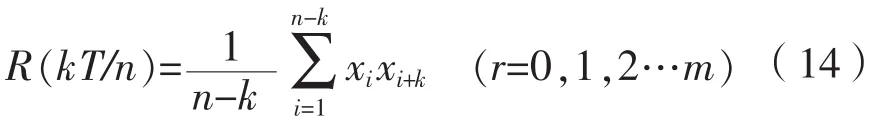
m為滯后的最大數目。

第二步：計算出各個k值的自相關函數Rk=并代入按梯形法求（12）式的積分近似值，即

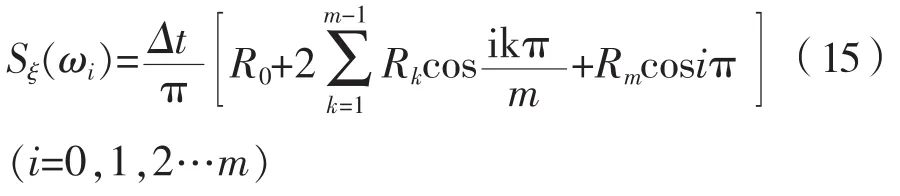
第三步：為了使波能譜曲線光滑，故采用Hamming窗函數平滑，處理之后波能譜如下：

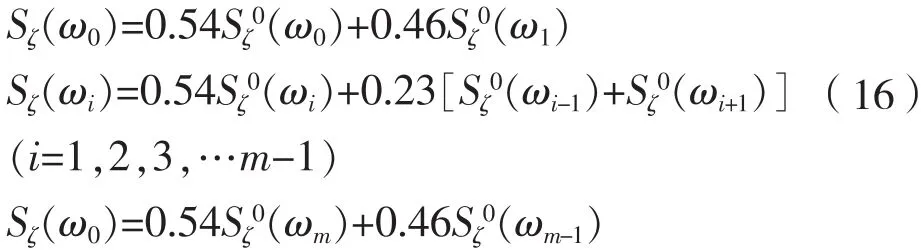
其中Hamming定義如下：

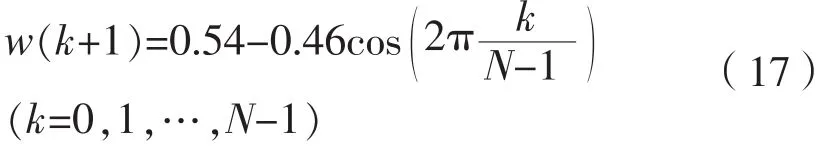
2.3.3 Bartlett法［3］

計算步驟

第一步：將具有N個數據的樣本分成L=N/M個子樣本，每個子樣本有M個觀測點，即

（n=0，1，…，M-1； j=1，2，…，L）式中： xj表示第j個子樣本的觀測值。

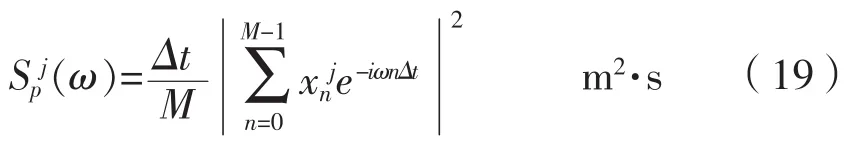
第三步：對子樣本的周期圖進行平均，即得Bartlett譜估計

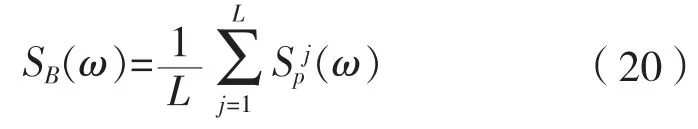
2.3.4 Welch方法［3］

計算步驟

第一步：將數據分為若干個子樣本，不同于Bartlett方法，此處允許數據有重疊。

式中：（n=0，1，…，M-1； j=1，2，…，S）

其中（ j-1）K是第j個子樣本的起始點。如果K=M，則序列不重疊(但是相鄰的連接)。在此選取K=M/2，此時S≈2N/M。

第二步：計算每個子樣本加窗的周期圖。

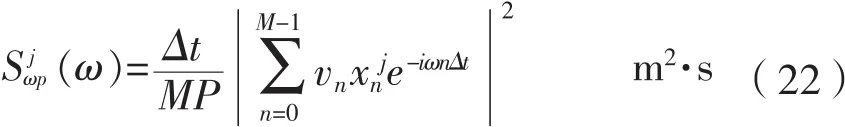
在此，窗函數選用Hanning窗：

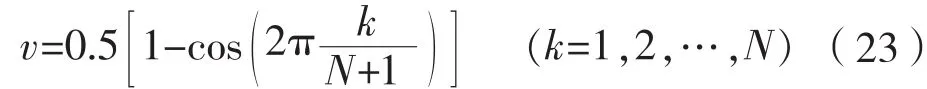
其中，P表示時間窗vi的“功率”：

第三步：對子樣本的加窗周期圖進行平均，即得Welch譜估計：

或Tk或Ek做圖。

此外，

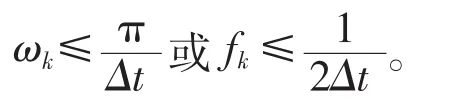
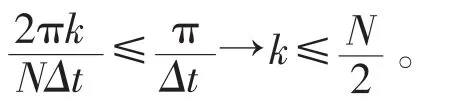
2.4 擬合度函數［4］

為了檢驗海浪模擬的效果，用偏差指數（D.I）描述設定輸入海浪譜與由仿真波浪估計的海浪譜的擬和程度［3］：

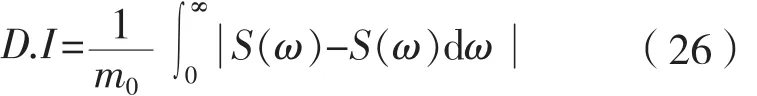
其中ω為角頻率，m0為零階矩

D.I越小，說明擬合程度越好。

3 計算結果與分析

ITTC譜中取有義波高0.5 m、周期5 s，根據式（1），得譜形如圖7。該譜即為目標靶譜，作為后續譜反演的參考譜形。

造出波形如圖8所示。

該波形均值為0.053 m、峰度2.954、偏度0.009 1，與理論理想不規則波均值為0、峰度為3、偏度為0已極為接近，以此可以認為是較符合實際的不規則波。圖9為該不規則波在空間上的仿真。

對上述不規則波進行0.5 s/次的采樣，并對采樣點進行譜分析，圖10～圖13是應用四種譜分析法以及Matlab編程求得的結果對比。

通過以上對比分析可以看到，直接法和Bartlett法精度較差，間接法精度最高，Welch法精度次之。

圖7 ITTC波浪譜

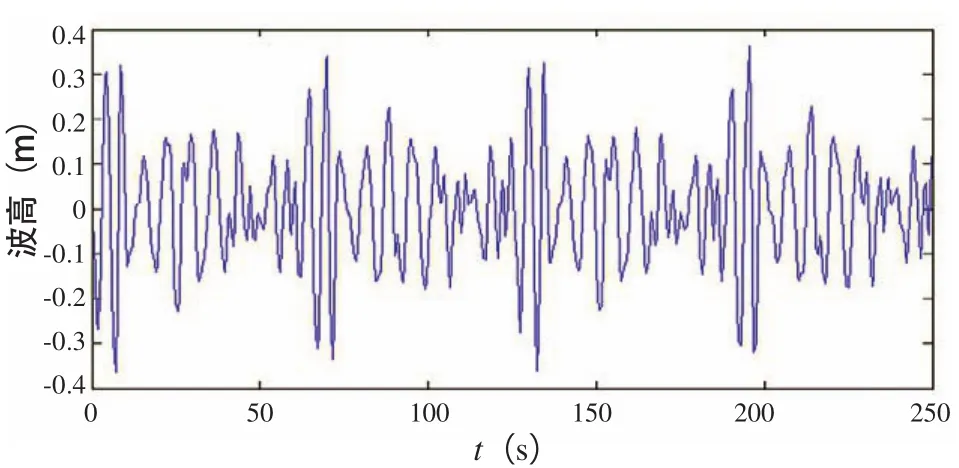
圖8 波形

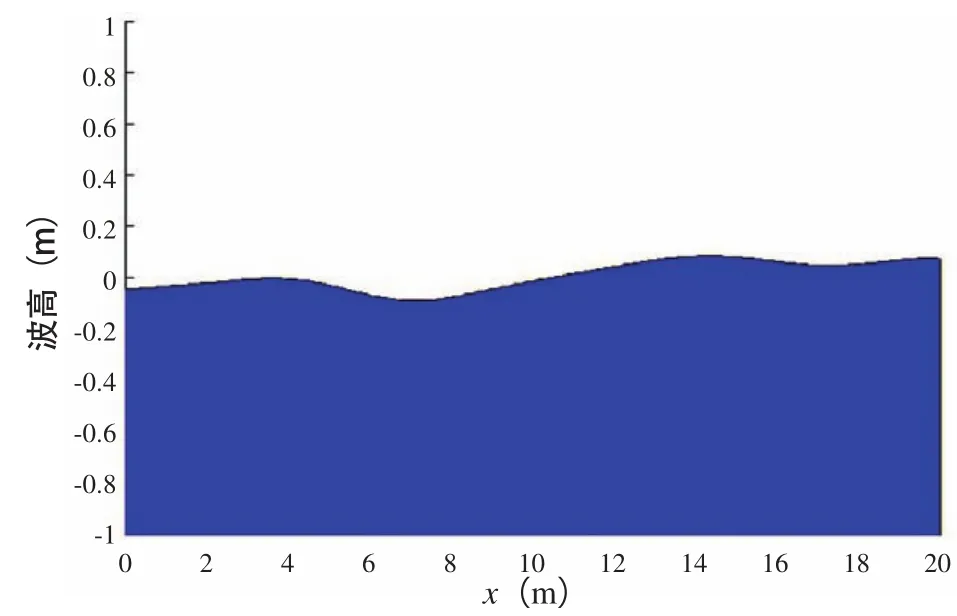
圖9 波浪模擬

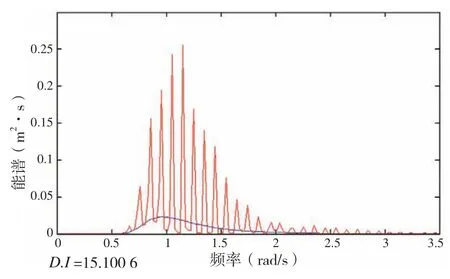
圖10 直接法

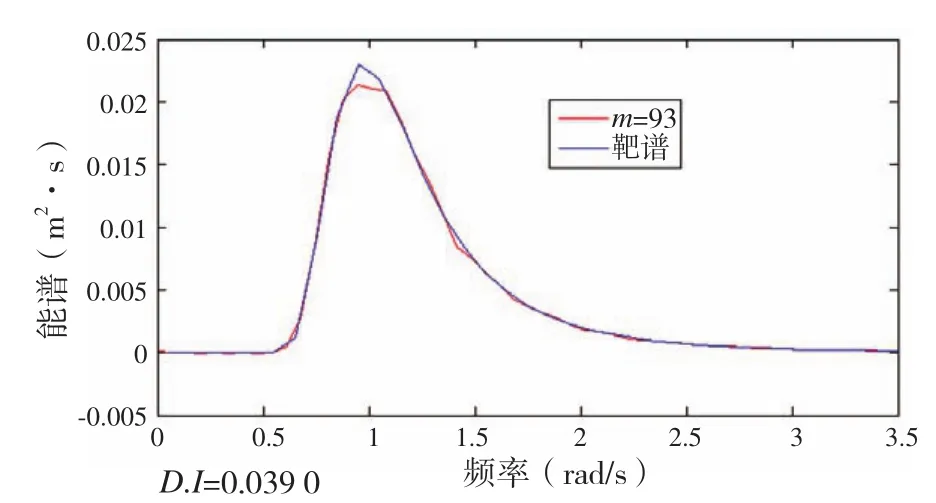
圖11 接間法

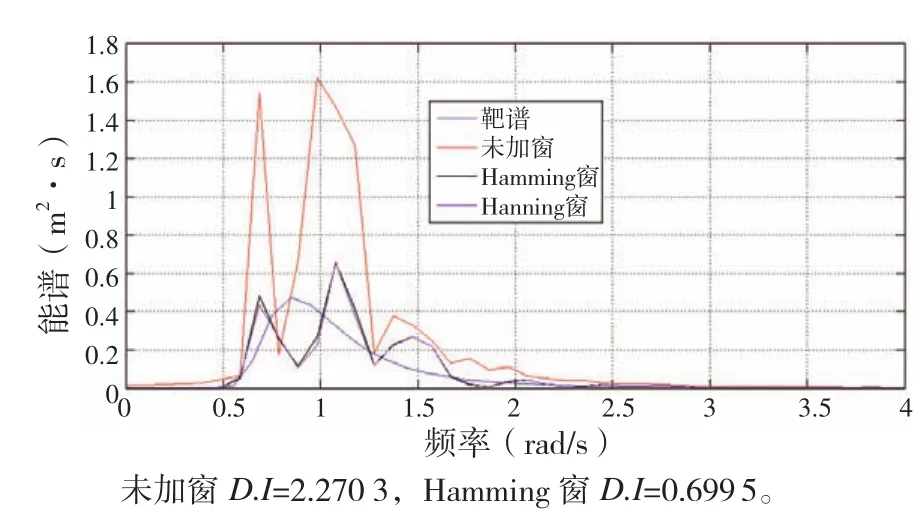
圖12 Bartlett法

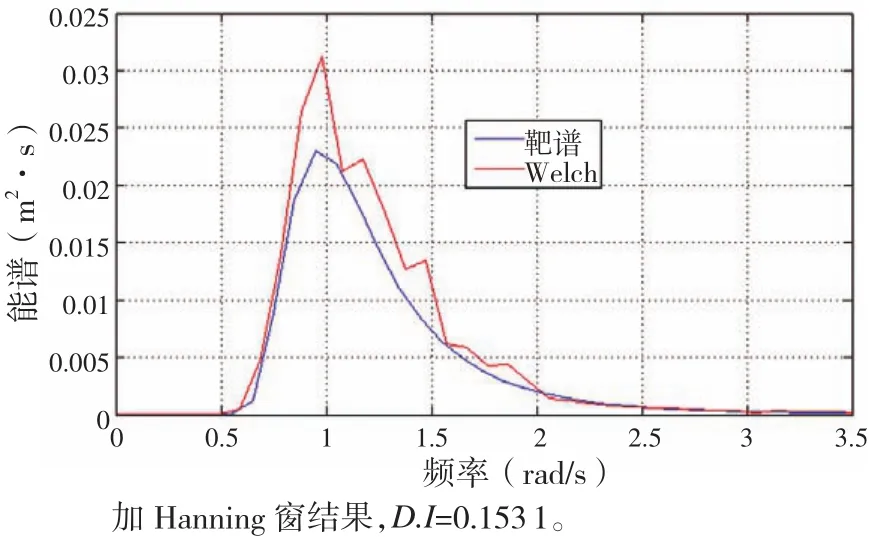
圖13 加Hanning窗的Welch法

上述四種方法在應用中都會產生誤差，這是因方法本身的算法缺陷造成的：

（1）直接法估計出來的方差不會隨著數據量的增加減少；當N 很大時，直接法的值是不相關的，從而導致計算出的功率譜出現“毛刺”（類似于高斯白噪聲），如圖10。因此，對于許多隨機信號，直接法統計精度較差，并且增加數據量也不能改善此精度，這是直接法存在的最根本缺陷。

（2）盡管間接法精度較高，但還是存在一定誤差。間接法在波浪譜反演過程中，存在“平滑”和“泄露”現象，第一副瓣寬度更是直接帶來偏差。

（3）Bartlett法和Welch法盡管在一定程度上能夠改善上述間接法的頻譜泄露，但并不能消除誤差。

（4）上述四種算法中，理論上的采樣點應該無限多，而實際應用中的采樣點較有限，因此產生截斷誤差。

在實際工程應用中，系統的穩定性異常重要。盡管間接法的精度在四種算法中最高，但間接法中，最大滯后數m是一個隨著信號而變化的量，無法在反演之前給定。對于任意信號，m值存在一個最優解，令譜反演質量達到最高。然而隨著信號的改變，該值的變化會降低控制系統的穩定性；當預設值偏離最優值較遠時，精度會趨向于直接法反演結果，從而導致精度非常低。因此，本文最終選取穩定性較好的Welch法作為譜反演方法。

4 結 論

本文以縱傾角信號為例，通過對以ITTC譜作為靶譜造波，應用四種譜反演方法，將結果與靶譜對比分析，最后得出滿足工程精度與穩定性要求的Welch法。該方法作為局部雙體氣墊船控制算法一個組成部分，為整個系統的穩定運行發揮巨大作用。

［1］ 李積德.船舶耐波性［M］.哈爾濱：哈爾濱工程大學出版社，2007：29-30.

［2］ 程佩清.數字信號處理教程［M］.北京：清華大學出版社，2007：37.

［3］ JOHN G P，DIMITRIS G M，數字信號處理：原理、算法與應用，張曉林，譯.第三版［M］.北京：電子工業出版社，2004：739-748.

［4］ 江林.由航行中船舶運動預報海浪［D］.哈爾濱：哈爾濱工程大學，2004：25.

［5］ 朱世強，武星軍，林建亞.海浪模擬的三維仿真研究［J］. 船舶工程，1999（6）：1-2.

［6］ 文圣常，海洋理論與計算原理［M］.北京：科學出版社，1985：228-232.

［7］ 趙希人．隨機過程應用［M］．哈爾濱：哈爾濱工程大學出版社，2003：94-106 .

［8］ 朱洪華，蔡建立.不規則波浪的仿真［J］.電腦知識與技術，2007（7）：202-203.

Research on method of wave spectrum inversion of PASCAT

XU Deng-hui ZOU Jing
(Multihull Ship Technology Key Laboratory of Fundamental Science for National Defense, Harbin Engineering University, Harbin 150001, China)

In order to make PASCAT regulate air flow with perception of sea state now and then, this paper analyzes and compares four methods, which deduce the wave spectrum signals from the amplitude of sea wave, in order to provide optimal control algorithm for selecting the inversion wave spectrum in the control system. The optimal algorithm is obtained by comparing the deduced wave spectrum with known spectrum. It shows that the results from Welch method are satisfying and can meet the engineering precision.

spectral analysis; ITTC spectrum; PASCAT; Welch method

U674.951

A

1001-9855（2014）02-0009-06

中央高校基本科研事業費專項資金資助（HEUCFD1303）。

2013-09-09；

2013-10-31

徐登輝（1987-），男，碩士，研究方向：氣墊船氣流量控制系統開發。鄒 勁（1965-），男，研究員，研究方向：船舶水動力。