鋼管混凝土柱對爆炸沖擊波影響的數(shù)值模擬研究

牛 操 盧永剛 陶俊林

(1.西南科技大學(xué)土木工程與建筑學(xué)院 四川綿陽 621010;2.中國工程物理研究院 四川綿陽 621900)

爆炸恐怖襲擊、工業(yè)生產(chǎn)、燃?xì)獗ǖ韧话l(fā)的爆炸事件均可能導(dǎo)致結(jié)構(gòu)的嚴(yán)重?fù)p壞或倒塌。對于柱子這種重要的承重構(gòu)件通常要考慮爆炸沖擊荷載的作用，因此研究工程結(jié)構(gòu)在爆炸沖擊荷載作用下的動力響應(yīng)具有重要的意義［1－2］。鋼管混凝土柱因其承載力高、塑形和韌性好而被廣泛應(yīng)用到建筑物中，目前對鋼管混凝土柱在準(zhǔn)靜態(tài)荷載作用下的力學(xué)響應(yīng)研究較多，但是在爆炸荷載沖擊作用下的響應(yīng)研究較少，本文通過LS－DYNA3D軟件對圓形、方形鋼管混凝土柱在爆炸沖擊荷載作用下的反應(yīng)進(jìn)行了數(shù)值模擬，著重分析了爆炸沖擊波的傳播過程，以及在不同比例距離下爆炸沖擊波在通過兩種截面柱子時超壓峰值的衰減及增大規(guī)律，通過進(jìn)行對比分析研究，獲得一定的規(guī)律性認(rèn)識，可用于指導(dǎo)工程實踐。

1 計算模型及材料模型

1.1 計算模型

本文引用的試驗為文獻(xiàn)［3］所進(jìn)行的實爆試驗，其目的是為鋼管混凝土構(gòu)件的抗爆炸荷載設(shè)計提供有益的試驗成果，也是后續(xù)數(shù)值模擬參數(shù)確定的有效基礎(chǔ)。有限元驗證模型如圖1所示。

圖1 有限元模型Fig.1 The finite element model

1.2 材料模型

為便于建模，材料的單位統(tǒng)一使用(g－cmus)量綱。

混凝土材料選用 HJC模型，是由 T.J.Holmquist，O.R.Johnson 和 W.H.cook 等［4］(1993)在第14屆國際導(dǎo)彈會議上針對混凝土材料在大應(yīng)變、高應(yīng)變率以及高圍壓條件下提出的計算模型。因其能夠較好地考慮壓縮強度的壓力相關(guān)性、應(yīng)變率效應(yīng)以及壓縮損傷累積效應(yīng)，從而得到廣泛應(yīng)用。其模型的狀態(tài)方程對于加載和卸載情況分3個區(qū)域:線彈性區(qū)、塑性過渡區(qū)和完全密實材料區(qū)。

在HJC模型中材料的等效強度定義為:

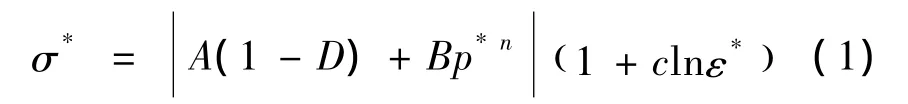
其中，σ*=σ/f′c為實際等效應(yīng)力與靜態(tài)屈服強度之比;p*=p/f′c為無量綱壓力，D(0≤D≤1)為損傷因子，由等效塑性應(yīng)變和塑性體積應(yīng)變累加得到:

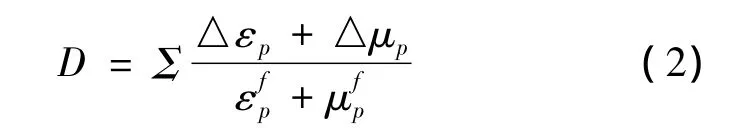
表1 混凝土參數(shù)表Table 1 The concrete parameters

炸藥采用TNT炸藥，LS－DYNA程序描述高能炸藥爆轟產(chǎn)物壓力－體積關(guān)系采用JWL狀態(tài)方程。高能炸藥爆轟產(chǎn)物的單元壓力p由狀態(tài)方程求得，JWL［5］狀態(tài)方程的p－V關(guān)系如下:

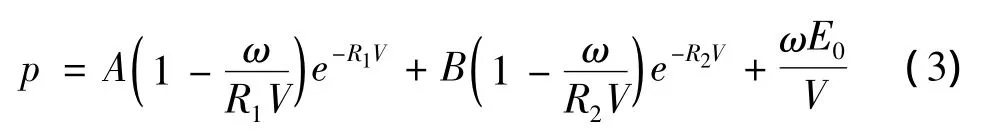
其中，V為相對體積，E0為初始內(nèi)能密度，參數(shù)A，B，R1，R2，ω為試驗確定的常數(shù)。

表2 TNT炸藥參數(shù)表Table 2 The TNT parameters

空氣的狀態(tài)方程采用MAT_NULL的材料本構(gòu)，主要參數(shù)為密度1.2929×10－3g/cm3，狀態(tài)方程采用*EOS_GRUNEISEN來表示。

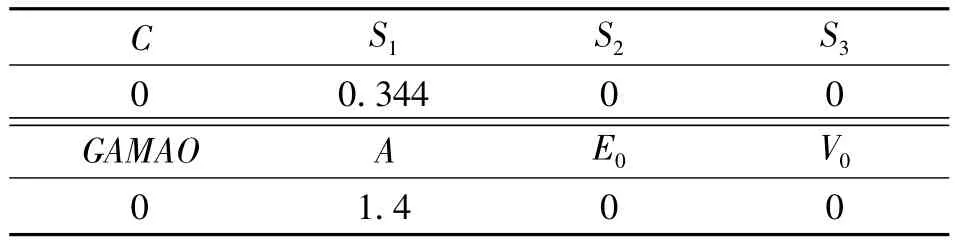
表3 空氣參數(shù)表Table 3 The air parameter

鋼材采用LS－DYNA中的MAT_PLASTIC_KINEMATIC本構(gòu)，它近似模擬鋼材的彈塑性階段，把塑性階段和強化階段簡化為一條斜直線，該模型包括等向強化、隨動強化及兩者的結(jié)合。

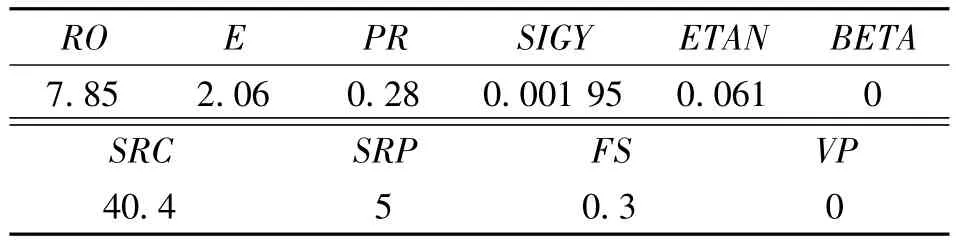
表4 鋼材參數(shù)表Table 4 The steel parameter

1.3 驗證結(jié)果

如圖2所示，在炸藥爆炸后，構(gòu)件在沿爆炸沖擊波的方向下的位移迅速增加，構(gòu)件跨中節(jié)點達(dá)到最大位移后，構(gòu)件回彈、震蕩。提取試驗中相同位置的單元的壓力值(見表5)及跨中節(jié)點位移時程曲線(見圖2)，并比較數(shù)值模擬結(jié)果與試驗結(jié)果(表5)。

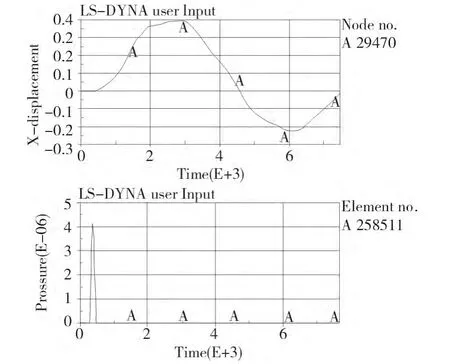
圖2 位移及壓力時程曲線Fig.2 The displacement and stress time history curves

表5 模擬結(jié)果Table 5 The simulation results

從表5可以看出數(shù)值模擬結(jié)果與試驗的數(shù)值比較接近，誤差均在10%以內(nèi)，由于其爆炸的復(fù)雜性，可以認(rèn)為其材料參數(shù)、本構(gòu)方程的選取較為合理，計算結(jié)果是可行的，模擬結(jié)果是可信的。

2 數(shù)值模擬中的網(wǎng)格尺寸效應(yīng)

在數(shù)值模擬過程中，當(dāng)所使用的材料參數(shù)都一樣時，其模擬的結(jié)果準(zhǔn)確性在很大程度上取決于劃分有限元模型時采用的網(wǎng)格尺寸的大小。由于爆炸數(shù)值模擬的復(fù)雜性，在實際的數(shù)值模擬過程中很可能出現(xiàn)在相同的網(wǎng)格尺寸下用于模擬比例距離較大的爆炸波傳播時可以得到比較理想的結(jié)果，但在比例距離較小的情況下所得到結(jié)果的誤差會變得很大，如果單純的減小網(wǎng)格的尺寸來提高計算的精度，這樣做必然會增加單元的個數(shù)，使得計算的時間大大增加，同時還會對計算機硬件水平提出過高的要求。因此，選用圖3所示的有限元模型模擬爆炸沖擊波在自由空氣中的傳播。

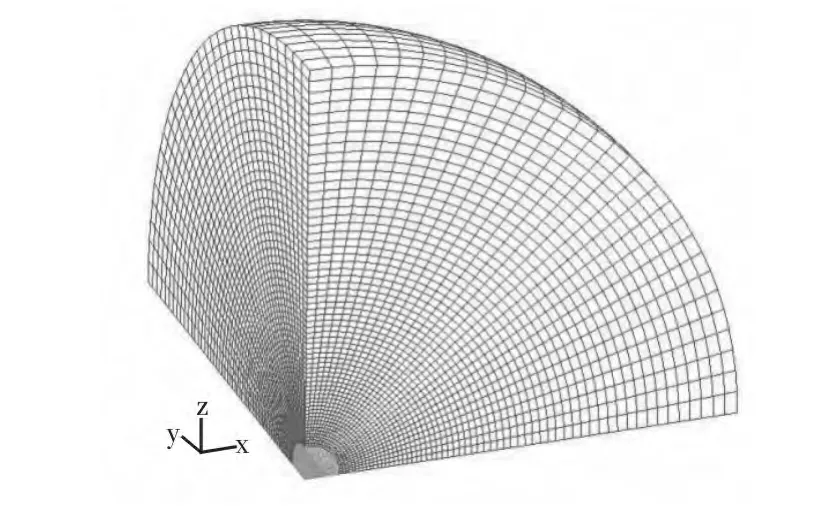
圖3 有限元模型Fig.3 The finite element model

炸藥的質(zhì)量取125 kg，單元網(wǎng)格的大小分別取0.5 cm，1 cm，2.5 cm，5 cm，10 cm，20 cm 進(jìn)行數(shù)值模擬，在比例距離Z=1的情況下得到了爆炸荷載超壓的時程曲線圖，如圖4所示。

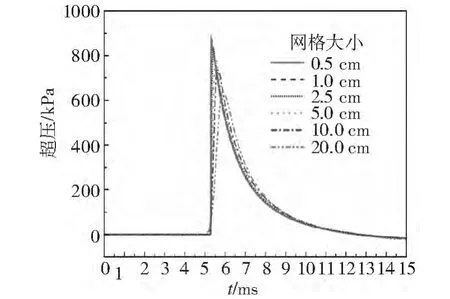
圖4 在不同網(wǎng)格大小下比例距離Z=1時的爆炸荷載時程曲線Fig.4 The explosion load time history curve under different mesh sizes and scaled distance Z=1

由圖4可以看出，網(wǎng)格劃分得越小，正超壓從零到峰值的斜率變得越大，而由峰值變到零的階段則變得陡峭，同時正超壓峰值升高。圖5、圖6分別給出了爆炸荷載參數(shù)在不同網(wǎng)格大小和不同比例距離情況下的敏感性，由圖5、圖6可知，網(wǎng)格的大小變化對爆炸荷載的沖擊波的到達(dá)時間影響不大，然而，劃分網(wǎng)格的尺寸大小對于爆炸荷載所產(chǎn)生的正超壓峰值影響較大，并隨著比例距離的減小，影響程度進(jìn)一步加深。

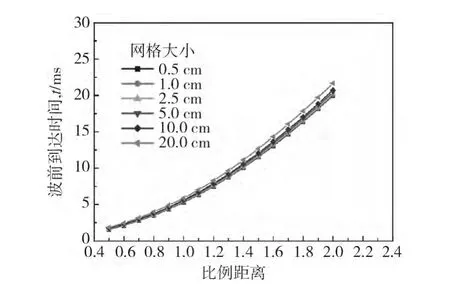
圖5 在不同網(wǎng)格大小和比例距離下的波前到達(dá)時間Fig.5 The wave front arrival time under different mesh sizes and scaled distance

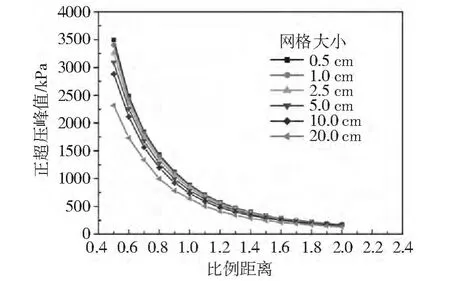
圖6 在不同網(wǎng)格大小和比例距離下的正超壓峰值Fig.6 The positive overpressure peak value under different mesh sizes and scaled distance

經(jīng)過分析可得，網(wǎng)格尺寸的大小對爆炸沖擊波正超壓峰值的影響比爆炸荷載波前到達(dá)時間的影響要大得多，即在數(shù)值模擬過程中，采用尺寸較大的網(wǎng)格模擬出的波前到達(dá)時間比較準(zhǔn)確，但是，模擬出的正超壓峰值就會存在很大誤差，為了既不影響正超壓峰值的準(zhǔn)確性又能最大限度發(fā)揮計算機性能，節(jié)省機時，在數(shù)值模擬過程中網(wǎng)格的大小選用2.0 cm，通過表5與美國軍事規(guī)范中的TM5－1300中大量爆炸超壓試驗數(shù)據(jù)進(jìn)行對比可知，數(shù)值模擬中的爆炸超壓峰值的誤差均在10%以內(nèi)，在工程領(lǐng)域內(nèi)是可以接受的。

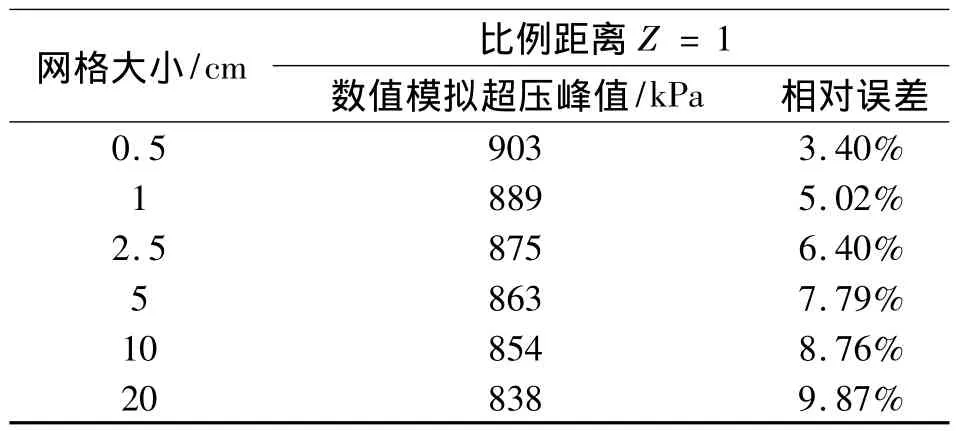
表5 在不同網(wǎng)格大小和比例距離下的正超壓峰值Table 5 The positive overpressure peak value under different mesh sizes and scaled distance

3 爆炸沖擊波的傳播和柱的影響

3.1 分析模型

分析模型如圖7所示。取圓形、正方形兩種截面的鋼管混凝土柱，其中柱高為3 m，混凝土，鋼材使用與試驗一樣的材料，假定柱子兩端為固支，鋼管混凝土柱只考慮爆炸沖擊波的作用，暫不考慮軸向荷載的作用。

圖7 分析模型Fig.7 The analysis model

3.2 爆炸沖擊波的傳播

在上面的數(shù)值模擬中，取截面為圓形的鋼管混凝土柱，比例距離Z=1時的工況，TNT在柱迎壓面中線的正前方，入射角為0度，得到了圖8、圖9所示爆炸沖擊波的傳播及其與柱子之間的相互作用過程圖。

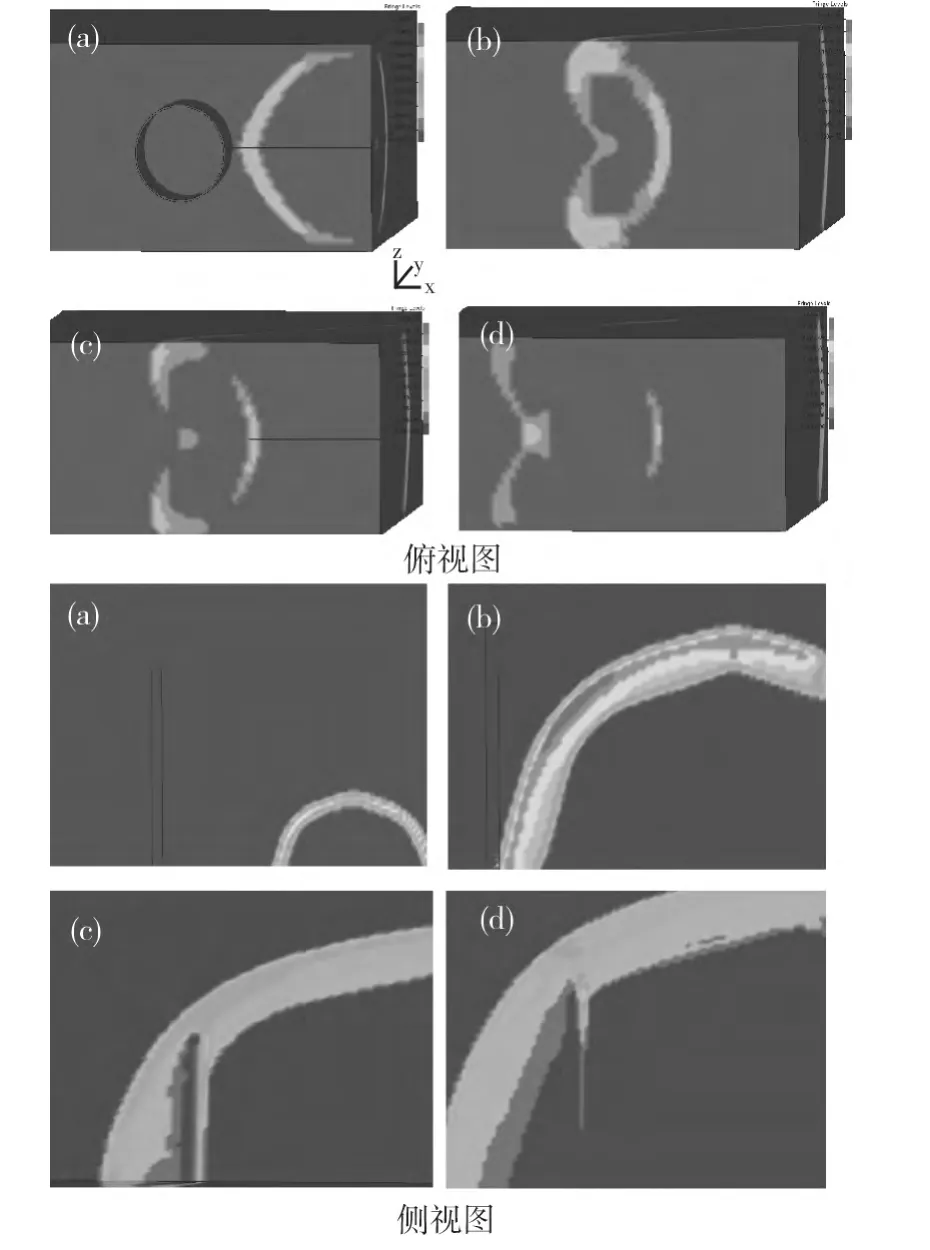
圖8 爆炸波的傳播Fig.8 The explosive shock wave propagation images

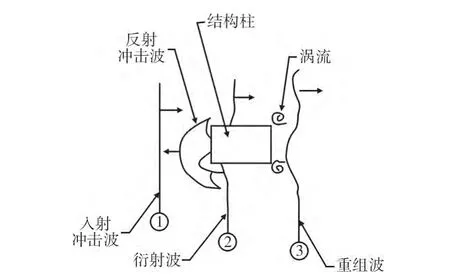
圖9 單柱與爆炸沖擊波相互作用示意圖Fig.9 The interaction diagram of a single column with explosive shock wave

從圖8、圖9可以看出，爆炸沖擊波先開始是呈球狀向前傳播，在碰到鋼管混凝土柱后形成反射波，沖擊波會繞過柱子并在柱子的兩側(cè)形成衍射波，并在柱子后面形成重組波。在鋼管混凝土柱迎壓面和后表面并沿高度方向上分別選取A，B，C三點，其中A點是柱頂，B點是柱中，C點是柱底，分別得到爆炸沖擊波的超壓時程曲線，如圖10、圖11所示。

圖10 柱迎壓面爆炸沖擊波超壓時程曲線Fig.10 The overpressure time history curve of the explosive shock wave from front surface of the column

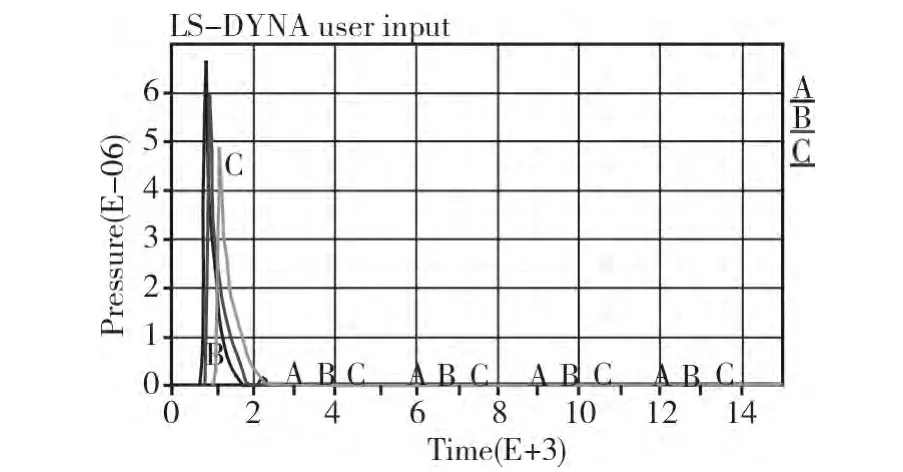
圖11 柱后表面爆炸沖擊波超壓時程曲線Fig.11 The overpressure time history curve of the explosive shock wave from rear surface of the column

由圖10、圖11可以看出，在柱的迎壓面，隨著目標(biāo)點高度的減小，爆炸沖擊波的超壓峰值明顯增大，由于有柱子阻擋的作用，爆炸荷載沖擊波在經(jīng)過柱子后，在柱子后表面的超壓峰值會變小且峰值相差不大。

3.3 柱截面形狀及尺寸對爆炸沖擊波的影響

為了更好地觀察爆炸沖擊波與鋼管混凝土柱前、后表面的相互作用過程，在隨后的數(shù)值模擬過程中取用了實際工程中比較常用的兩種截面柱:方形柱和圓形柱，其中方形截面尺寸在30～100 cm范圍內(nèi)變化，圓形截面柱子的半徑在25～50 cm范圍內(nèi)變化。

3.3.1 爆炸沖擊波的反射

沖擊波在傳播過程中遇到柱子的阻擋，會在其表面形成反射波，在前人的研究中發(fā)現(xiàn)反射波的超壓峰值要遠(yuǎn)高于入射波，通過引入PrF(0)=AppPsF就能更好地研究沖擊反射波與鋼管混凝土柱截面尺寸的關(guān)系，其中PrF(0)表示爆炸沖擊波反射超壓峰值，App代表反射超壓增大系數(shù)，PsF表示柱子底部迎壓面中點處的入射波超壓峰值。數(shù)值模擬結(jié)果如圖12所示，隨著鋼管混凝土柱截面尺寸的變化對柱子迎壓面底部中點處的反射超壓峰值的增大系數(shù)有著明顯的影響，選取柱子底部中點處，圓形截面柱與方形截面柱情況下，當(dāng)比例距離不變時，隨著柱截面尺寸的增大，反射超壓峰值的增大系數(shù)會增大，當(dāng)柱截面尺寸不變時，隨著比例距離的增大，其反射超壓峰值的增大系數(shù)會降低，這可能是由于截面尺寸增加導(dǎo)致反射面積增大，使得爆炸沖擊波在受到柱子阻擋的面積增加，產(chǎn)生更多的反射波，讓沖擊波的反射強度得到進(jìn)一步加強。

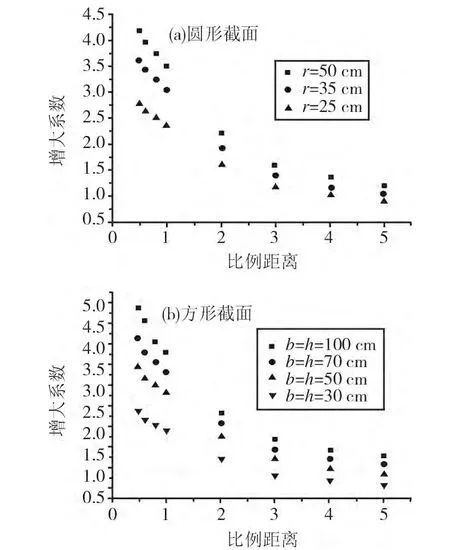
圖12 不同截面尺寸和比例距離情況下的反射超壓峰值增大系數(shù)Fig.12 The reflection coefficient of the overpressure peak value increases under different section size and scaled distance

3.3.2 爆炸沖擊波的繞射

當(dāng)爆炸沖擊波經(jīng)過柱子，會產(chǎn)生一部分衍射波，其強度下降非常快，可以像研究沖擊波發(fā)射時一樣，通過引入PrR(0)=RppPrF來更好地研究爆炸沖擊波繞射過后的衰減程度與鋼管混凝土柱截面尺寸的關(guān)系，其中PrR(0)表示柱子背壓面底部中點處的爆炸沖擊波超壓峰值，Rpp為超壓峰值折減系數(shù)。選取柱子底部中點處，數(shù)值模擬結(jié)果如圖13所示。兩種截面柱在比例距離由1變到2時，超壓峰值折減系數(shù)有個比較明顯的突變，且在比例距離小于1時，柱截面尺寸的改變對超壓峰值的折減系數(shù)影響不是很大;比例距離大于2時，隨著柱截面尺寸的增大，超壓峰值的折減系數(shù)會減小;當(dāng)柱截面尺寸不變時，隨著比例距離增大，其超壓峰值的折減系數(shù)會變大，這可能是由于當(dāng)柱截面尺寸增大后，爆炸沖擊波的衍射作用被削弱，經(jīng)過柱子后，爆炸沖擊波強度變小，所以導(dǎo)致在柱子后表面上的超壓峰值會降低。

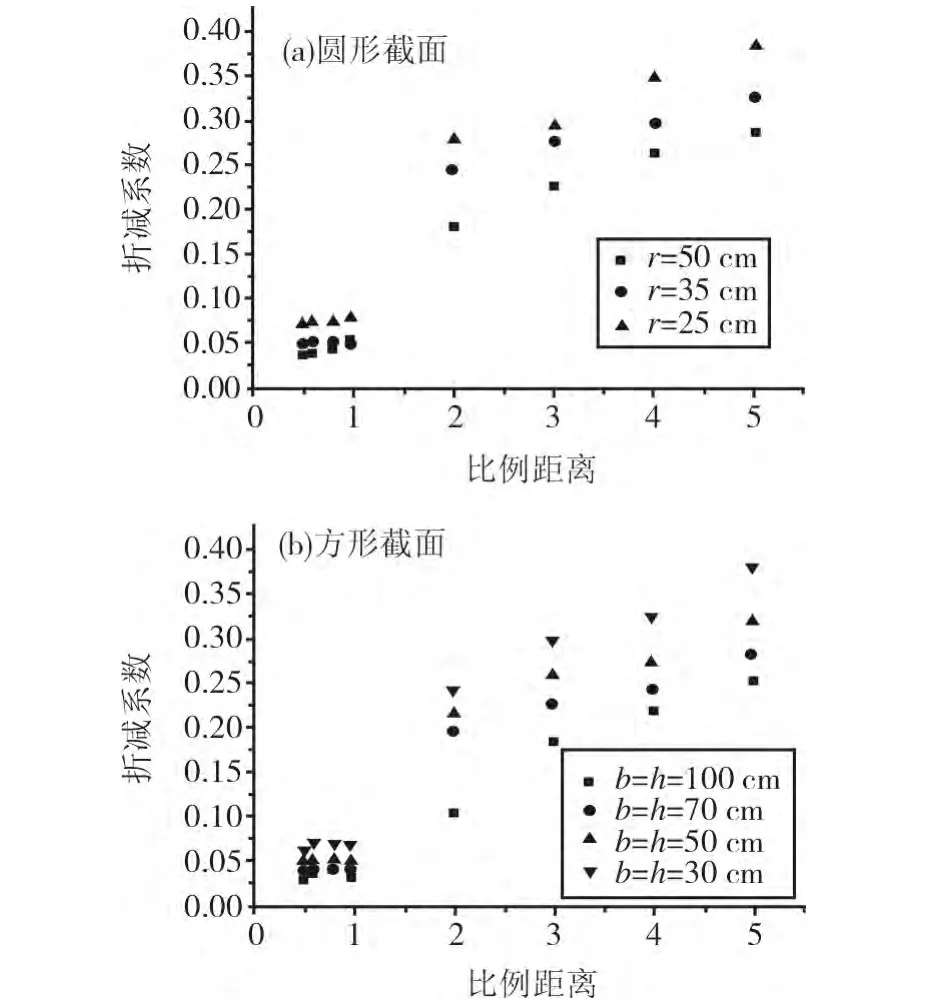
圖13 不同截面尺寸和比例距離情況下的衍射超壓峰值折減系數(shù)Fig.13 The reduction factor of the diffraction peak overpressure under different sectional sizes and scaled distance

4 結(jié)論

本文結(jié)合有關(guān)文獻(xiàn)中的理論及試驗研究，初步得到以下結(jié)論:(1)在柱的迎壓面，隨著目標(biāo)點高度的減小，爆炸沖擊波的超壓峰值明顯增大，由于有柱子阻擋的作用，爆炸荷載沖擊波在經(jīng)過柱子后，在柱子后表面的超壓峰值會變小且峰值相差不大。(2)爆炸沖擊波反射特點為:當(dāng)比例距離一定時，兩種截面柱的反射超壓峰值的增大系數(shù)均隨著柱截面尺寸的增大而增大，爆炸沖擊波的反射波強度會進(jìn)一步增強，當(dāng)柱截面尺寸不變時，隨著比例距離增大，其反射超壓峰值的增大系數(shù)會降低，反射波的強度增加比較有限。(3)爆炸沖擊波繞射的特點為:繞射的部分爆炸波繞射過結(jié)構(gòu)柱后其強度會急劇減弱。當(dāng)比例距離小于1時，柱截面尺寸的改變對超壓峰值的折減系數(shù)影響不大，所以繞射波的強度衰減不明顯;當(dāng)比例距離大于2時，隨著柱截面尺寸的增大，超壓峰值的折減系數(shù)會減小，繞射波的強度會變小。(4)在數(shù)值模擬中網(wǎng)格尺寸的大小對沖擊波峰值影響較為明顯，但對波的傳播時間影響不大。

［1］鐘善桐，鋼管混凝土統(tǒng)一理論——研究與應(yīng)用［M］.北京:清華大學(xué)出版社，2006.

［2］錢七虎.反爆炸恐怖安全對策［M］.北京:科學(xué)出版社，2005.

［3］肖志華，何斌.鋼管混凝土構(gòu)件的爆炸荷載試驗研究［J］.機械，2012，(4):8 －12.

［4］HOLMQUIST T J，JOHNSONN G R，COOK W H.A computational constitutive model for concrete subjected to large strains，high strain rates and high pressures［J］.14rhInt.Sym.Ballistics，1993，591 －600.

［5］白金澤.LS－DYNA3D理論基礎(chǔ)與實例分析［M］.北京:科學(xué)出版社，2005.

［6］尚曉江，蘇建宇.ANYSYS/LS－DYNA動力分析方法與工程實例［M］.北京:中國水利水電出版社，2005.