基于時序關聯規則的設備故障預測方法研究

甘超，陸遠，李娟，胡瑩，鄒博宇

(1.南昌大學機電工程學院，江西南昌330031;2.中國北方車輛研究所車輛傳動重點實驗室，北京100072)

隨著科學技術的進步和制造業的發展，機械設備日益呈現復雜化、大型化和多功能化［1］。設備維護是保障設備穩定和可靠運行的重要手段。設備的維修方式從早期的無計劃維修到預防性維修逐步向基于狀態維修 (Condition-Based Maintenance，CBM)［2］方式轉變，而設備故障預測是CBM的關鍵。近年來，國內外針對設備故障預測的研究取得了巨大的成果，主要有王寧等人［3］提出的一種基于時變轉移概率的隱半Markov模型，用于設備運行狀態的識別和故障預測;CAESARENDRA等［4］通過仿真和實驗的故障數據，利用概率論和支持向量機來預測故障的衰減過程;武兵等人［5］提出了利用支持向量回歸技術對多個特性量進行并行預測，并對各類特征和預測結果進行趨勢分析。文中提出了基于時序關聯規則的設備故障預測方法，將故障數據轉換為時序項集矩陣，利用Apriori改進算法和頻繁時序關聯規則查找算法，求出時序項集矩陣的頻繁時序關聯規則，為管理人員提供決策支持。最后給出了該方法的可行性實例驗證。

1 故障數據模型

隨著設備使用壽命的增多，發生故障的概率越來越大，企業能采集到很多故障數據。這些故障數據具有動態性、大量性、冗余性、噪聲大等特點。基于這些特點，利用Apriori傳統關聯規則算法的思想［6－7］，將故障記錄表中的數據按照設備編號進行分組，并記錄故障發生時間，剔除無效的數據，得到時序故障數據模型。如表1所示。

表1 時序故障數據模型

模型的數據結構需要滿足兩個性質:

性質1:每個事務T有唯一的設備編號標識，事務中的所有數據項對應設備的故障數據。不存在相同設備編號的兩個事務。

性質2:事務中的數據項都由一個二元組＜i，t＞表示，稱為時序項。其中，i為項 (此處為故障代碼)，t為時序項的時間戳。

為了便于利用關聯規則算法求出頻繁項集，同時為了更清楚地表達設備編號和故障代碼之間的關系，將表1時序故障數據模型轉換為類似于位圖的形式，如表2所示。其中 (1，T)表示設備在時間T發生了某故障，＜0，0＞表示設備從來沒有發生某故障。同一設備可能在不同時間發生多次某故障，所以單元格中可能出現多個時序項。

表2 時序故障數據轉換模型

所以，設備故障關系數據可以表示為矩陣D:

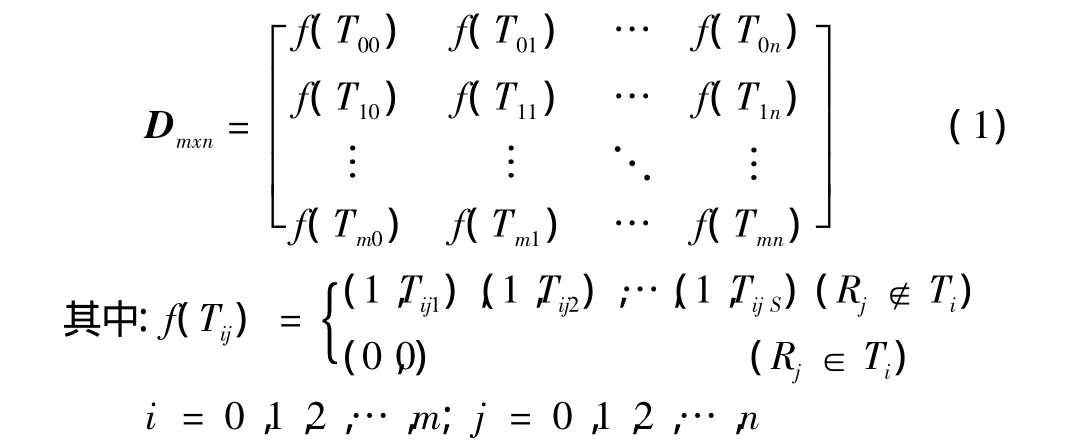
其中:Rj為表示故障代碼;Ti為表示設備編號。Rj∈Ti表示設備Ti在時間Tij1，Tij2，…TijS發生了故障Rj;S表示Ti發生故障Rj的次數;TijS表示故障發生時間;Rj?Ti表示設備Ti從來沒有發生故障Rj。

將故障數據庫轉換為形如式 (1)矩陣，可以形象地描述設備和故障代碼的關聯關系。這種故障數據模型可以減小掃描數據庫的次數，降低計算機配置要求，提高算法的運行效率。

2 時序關聯規則相關數據模型的概念

定義1，時序項集矩陣。矩陣的每一行代表一個事務Ti，每一列代表一個項目Ij。當第i個事務包含第j個項目時，對應位置的值為 {(1，Tij1)， (1，Tij2)，…， (1，TijS)}，TijS表示時序項的時間戳，S為包含項目的個數;當第i個事務不包含第j個項目時，對應位置的值為 (0，0)。形如式 (1)的矩陣就是一個時序項集矩陣。

定義2，時序候選項集矩陣。用關聯規則算法，對時序項集矩陣剪枝操作后，刪除不滿足要求的行和列，重新計算，得到時序候選項集矩陣。

定義3，時序關聯規則。A，B是項集I的子集，滿足A?I，B?I，且A∩B=φ，t表示在同一個事務Ti中項集B在項集A之后t的時間發生。時序關聯規則是形如以下的蘊含式:

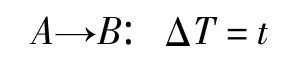
定義4，時序規則模式。在由關聯規則算法計算出的頻繁N項集中，對于某個頻繁項集的子集A，由該子集在ΔT時間之后發生補集B，稱為時序規則模式。可以表示為A→B。

定義5，最大同一時序關聯規則。

定義時間模式判別運算，用運算符“∩”表示。運算表達式為:ΔT1∩ΔT2∩…∩ΔTi，運算結果是ΔT1，ΔT2，…ΔTi中相同個數的最大值。如:7∩6∩7∩7∩5∩6=3。

定義時間模式相減運算，用運算符“－”表示。運算表達式為:(A，Ta)－(B，Tb)=A→B:ΔT=(Tb－Ta)。

時序規則模式A→B，在頻繁時序項集中有j條記錄支持該模式，表示為 {(A，Ta1)，(B，Tb1)}，{(A，Ta2)， (B，Tb2)}，…， {(A，Taj)， (B，Tbj)}，其中 ΔT1=Tb1－Ta1，ΔT2=Tb2－Ta2，ΔTj=Tbj－Taj。若 ΔT1∩ΔT2∩…∩ΔTj=number，且對應的相同值為t'，則稱時序關聯規則A→B:ΔT=t'為時序規則模式A→B的最大同一時序關聯規則。

定義6，頻繁時序關聯規則。是指某時序規則模式的最大同一時序關聯規則支持度不小于最小支持度的時序關聯規則。

3 算法基本原理

由上文可知，在頻繁N項集的所有時序規則模式中，不一定每個時序規則模式的最大同一時序關聯規則都能滿足最小支持度，所以設備故障預測可以轉換為求頻繁項集的頻繁時序關聯規則。

(1)求時序項集矩陣中所有頻繁項集

Apriori算法是關聯規則挖掘中最經典的算法。由于挖掘的對象是海量的故障數據，傳統的挖掘算法有兩個弊端［8－9］:①重復掃描數據庫，數據庫開銷大;②迭代次數多，處置的數據量大，算法適應性差。文中提出一種Apriori改進算法，將故障數據庫轉換為形如式 (1)的矩陣。對數據庫的操作轉換為對矩陣的處理，減小了對計算機配置的要求，提高了算法效率和計算速度。利用該關聯規則算法找出時序項集矩陣中所有頻繁項集。

(2)求頻繁時序關聯規則

在所有頻繁項集中，找到每個頻繁項集的所有時序規則模式。通過最小支持度，篩選出所有頻繁時序關聯規則，最后做出相應的決策。

圖1為算法在設備故障預測中的應用過程。

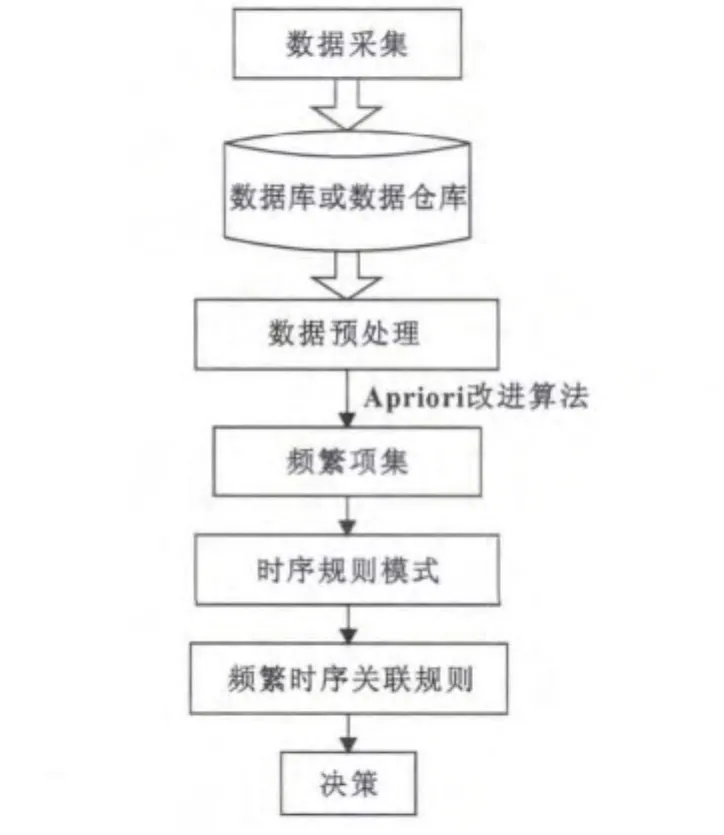
圖1 算法在設備故障預測中的應用過程

4 算法描述

文中主要用到兩個算法:Apriori改進算法和頻繁時序關聯規則查找算法。將詳細描述這兩個算法。

4.1 Apriori改進算法描述

基于Apriori改進算法找出時序項集矩陣中的所有頻繁項集步驟如下:

(1)采集的故障數據預處理。將沒有噪聲的數據轉換為形如式 (1)的時序項集矩陣M，每個事務代表一臺設備，每個項目代表一個故障代碼。在進行矩陣計算時，矩陣時序項的值用d［i，j］代替，矩陣時序項的值若為 (0，0)，d［i，j］=0，否則d［i，j］=1。

For(int i=0;i＜m;i++){//將故障數據轉換為時序項集矩陣

(2)增加第 (m+1)行和第 (n+1)列，得到時序候選項集矩陣M0。矩陣M每行求和，得到每臺設備發生的故障代碼數;每列求和，得到故障代碼的設備支持數。生成 (m+1)行和 (n+1)列，將支持數從大到小排列，得到矩陣M0。

order by d［m+1，j］desc// 矩陣按故障代碼的設備支持數降序排列

(3)計算時序項集最小支持數 minSupCount，minSupCount等于時序項集最小支持度minSup與事務數的乘積，也就是與設備數的乘積，并取不小于它的最小整數。

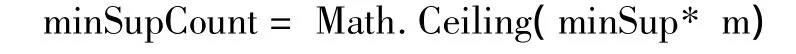
其中:Ceiling表示不小于給定數的最小整數，m為事務的數量。

(4)求頻繁K項集L［k］

在求頻繁K項集支持數時，對每項所在的列做向量內積運算，只有所有項對應的值均為1時，結果才為1，否則為0。如果某設備的項目數小于k，則該設備所在的行d［i，j］值為“1”的數目也小于k，所以可以直接刪除該行。

刪除不滿足要求的行后，重新進行列運算，并按支持數從大到小排列。

刪除支持數小于最小支持數的列，重新進行運算。最后得到時序候選項集矩陣Mn。

通過向量內積運算計算各項集的支持數，與最小支持數比較，得到頻繁K項集L［k］。

for(int i=0;i＜m;i++)//計算頻繁項集L［k］，刪除項目數小于k的行;

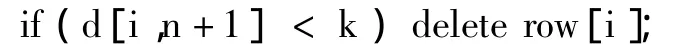
//刪除i行后，i行后面的事務往前移動;m－－;//行數減1;

for(int j=0;j＜n;j++)//刪除支持數小于最小支持數額列;

//刪除j列后，j列后面的項目往前移動;

n－－;//列數減1;

//重新進行行列求和;

//做向量內積運算得到各個候選項集的支持數s;

L［k］={C［k］|s＞ =minSupCount};// 得到頻繁項集 L［k］;

4.2 頻繁時序關聯規則查找算法描述

為了便于描述算法，對于時序項集((I)，T)提出以下方法:

時序項集((I)，T)，其中I為項集，T為時序項集的時間戳，T的值為I中最后一個時序項的時間戳。定義運算符“#”，表達式#((I)，T)，若T為所有時序項中的最大值，輸出1，否則輸出0。

算法偽代碼如下:

輸入:所有的頻繁項集List{L［K］}，最小支持度minSup

輸出:頻繁時序關聯規則

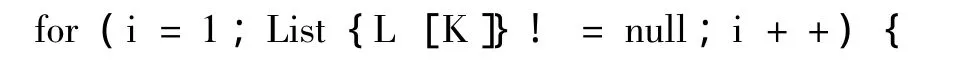
for all pattern{//每個頻繁項集的所有時序規則模式做循環;

按照”→”拆分時序規則模式為時序項集A和時序項B;

//時序規則模式相減運算;

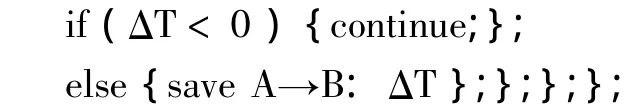
//時間大于0，保存結果;

ΔT1∩ΔT2∩…∩ΔTi//時間模式判別運算;

計算最大同一時序關聯規則的支持度，與最小支持度比較，輸出頻繁時序關聯規則;

5 實例驗證

舉例說明，如表3所示，假設為某汽車企業處理后的時序故障數據，其中設備編號為同一類型的設備。

表3 時序故障數據

掃描故障數據庫，表3數據轉換為時序項集矩陣M:

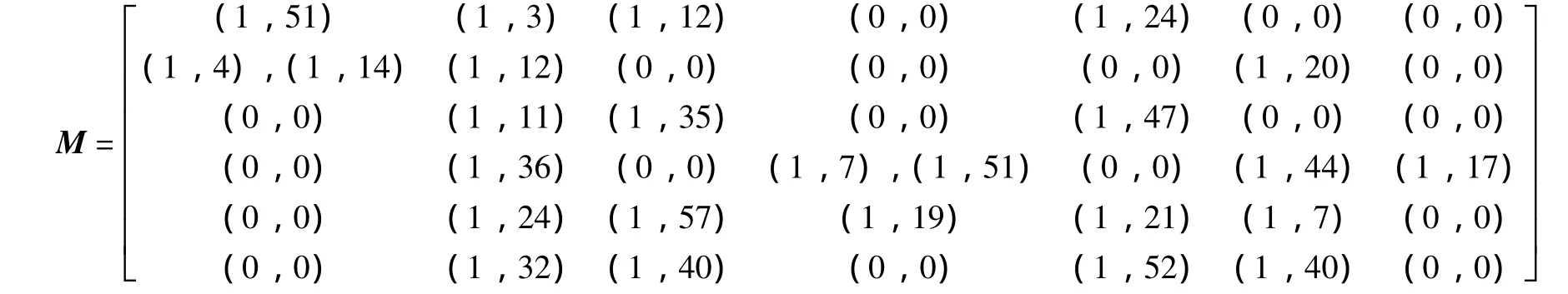
時序項的值若為 (0，0)用0代替，否則用1代替，分別對行列求和，并按項目支持數降序排列，得到矩陣M0:

設最小支持度為40%，最小支持數minSupCount=40% ×6=2.4，取整數3。

求頻繁1項集L［1］。刪除支持數小于3的列，重新計算后的矩陣為M1:

所以，頻繁1 項集L［1］={{P02}，{P03}，{P05}，{P06}}。

求頻繁2項集L［2］。刪除矩陣最后一列項目數小于2的行，此處沒有小于2的行，故M2=M1。計算候選2項集的支持數:

所以，頻繁 2 項集L［2］={{P02，P05}，{P02，P06}，{P02，P03}，{P05，P03}}。

求頻繁3項集L［3］。刪除矩陣最后一列項目數小于3的行，刪除支持數小于3的列，重新計算后的矩陣為M3:

計算候選3項集的支持數:

SupCount(P02*P05*P03)=4;

所以，頻繁 3 項集L［3］={{P02，P03，P05}};頻繁3項集是最大頻繁項集。

所有頻繁項集為:

找到每個頻繁項集的所有時序規則模式，根據頻繁時序關聯規則查找算法，輸出頻繁時序關聯規則。限于篇幅，文中以頻繁3項集L［3］為例介紹。

L［3］的所有時序規則模式為:P02P05→P03，P05P02→P03，P02P03→P05，P03P02→P05，P03P05→P02，P05P03→P02。

對于P02P05→P03，在時序候選項集矩陣M3的第一條記錄中，拆分時序規則模式，對應的時序項集為((P02，P05)，24)和(P03，12)，#((P02，P05)，24)=1，做時間模式相減運算:

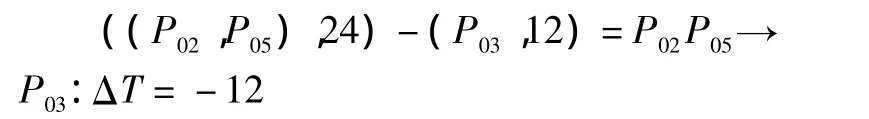
由于ΔT＜0，放棄該記錄，繼續循環，同理計算，其他記錄的ΔT都小于0，故無最大同一時序關聯規則，支持度小于最小支持數3。

同理可知，P05P02→P03，P03P02→P05，P03P05→P02，P05P03→P02的支持度都小于最小支持數3，放棄這些規則模式。

對于P02P03→P05。每條記錄的時序關聯規則為:

12∩12∩12=3，故矩陣中有3條記錄支持時序關聯規則P02P03→P05:ΔT=12，不小于最小支持數3。

輸出時序關聯規則P02P03→P05:ΔT=12，可以描述為:這種類型的設備首先發生故障P02，再發生故障P03，之后的12個單位時間內會發生故障P05。

6 總結

設備故障預測是提高設備穩定性和可靠性的重要方法。文中提出了基于時序關聯規則的設備故障預測方法，考慮故障數據的特點，應用Apriori傳統關聯規則算法的思想，將故障數據轉換為時序項集矩陣，利用Apriori改進算法和頻繁時序關聯規則查找算法，求出時序項集矩陣的頻繁時序關聯規則，從而預測設備故障趨勢，為管理人員制定維修決策提供可靠依據，減小設備維護支出，提高了設備維護效率。該算法的缺點是沒有考慮設備保養的情況，下一步將針對保養設備，增加反饋機制，調整現有算法規則進行研究。

［1］趙永滿，梅衛江，吳疆，等.機械故障診斷技術發展及趨勢分析［J］.機床與液壓，2009，37(10):255 －256.

［2］YAM R C M，TSE P W，Li L，et al.Intelligent predictive decision support system for condition-based maintenance［J］.International Journal of Advanced Manufacturing Technology，2001，17(5):383 －391.

［3］王寧，孫樹棟，李淑敏，等.基于DD-HSMM的設備運行狀態識別與故障預測方法［J］.計算機集成制造系統，2012(8):1861－1868.

［4］CAESRENDRA W，WIDODO A，YANG B S.Combination of Probability Approach and Support Vector Machine Towards Machine Health Prognostics［J］.Probabilistic Engineering Mechanics，2011，26(2):165 －173.

［5］武兵，林健，熊曉燕.基于支持向量回歸的多參數設備故障預測方法［J］.振動測試與診斷，2012(5):791－795，864.

［6］AGRAWAL R，IMIELINSKI T，SWAMI A.Mining Sssociation Rules between Sets of Items in Large Databases［C］//Proceedings of the 1993 ACM SIGMOD International Conference on Management of Data.Washington DC，United states，1993:207 －216.

［7］王愛平，王占鳳，陶嗣干，等.數據挖掘中常用關聯規則挖掘算法［J］.計算機技術與發展，2010(4):105－108.

［8］崔貫勛，李梁，王柯柯，等.關聯規則挖掘中Apriori算法的研究與改進［J］.計算機應用，2010(11):2952－2955.

［9］朱其祥，徐勇，張林.基于改進Apriori算法的關聯規則挖掘研究［J］.計算機技術與發展，2006(7):102－104.