廢舊零部件剩余使用壽命評估方法研究
張旭剛,張華,江志剛
(武漢科技大學機械自動化學院,湖北武漢430081)
廢舊產品再制造的可行性和可行度是發展再制造產業面臨的首要問題,特別是產品附加值高的關鍵零部件是否可以再利用或修復而不需要替換。由于廢舊產品一般都是經歷過一次或多次服役周期,其零部件是否還有剩余使用壽命,其剩余使用壽命能否維持下一個壽命周期是決定廢舊零部件能否進行再利用或再制造的前提[1]。因此,有必要對廢舊零部件進行剩余使用壽命的評估。
目前,針對廢舊零部件剩余使用壽命評估問題,國內外學者展開了廣泛的研究。DATTOMA等提出了非線性連續損傷力學模型,通過材料在不同載荷水平下的損傷演化程度來預測工件的疲勞壽命[2]。MAKKONEN建立了零部件全壽命模型,通過零部件的裂紋尺寸來預測剩余壽命[3]。MOHANTY等研究了應用多層感知器神經網絡預測工件疲勞壽命的問題[4]。KIM等開發了專家系統來預測工件在可變荷載下的疲勞裂紋萌生壽命[5]。吳學仁等綜述了基于小裂紋理論的疲勞全壽命預測方法,將斷裂力學與裂紋閉合概念結合起來分析和預測航空材料的疲勞全壽命[6]。呂凱波等介紹了一種采用疲勞有限元分析軟件MSC-FATIGUE來對結構件進行疲勞壽命預測的方法[7]。張景柱等建立了磨損失效壽命仿真預測的數學模型,利用ADAMS軟件模擬零部件各種工況下的運動并對其壽命進行分析[8]。文獻 [9-10]對進化算法在壽命預測中的應用進行了研究。
以上壽命預測方法歸納起來主要包括以下3種:(1)基于力學的剩余使用壽命評估方法;(2)基于有限元模擬計算的剩余使用壽命評估方法;(3)基于信息技術的剩余使用壽命評估方法。這些研究在發電設備、航空航天、石油化工、數控加工、冶金工業等行業與領域取得了重要進展。但是大部分的剩余使用壽命評估主要集中在研究材料或結構的失效與破壞機制,建立基于力學模型和有限元仿真的剩余使用壽命評估方法。對于單一失效機制的零部件來說,基于力學的壽命評估模型較為可行,而在產品的實際使用過程中,零部件往往是由于多種失效模式共同作用而失效的。因此,該方法具有一定的局限性。對于基于有限元模擬計算的剩余使用壽命評估模型來說,預測精度依賴于對服役條件了解的準確程度,預測結果具有不確定性。基于信息技術的剩余使用壽命評估方法以反映零部件運行狀態的數據為基礎,建立它們與剩余使用壽命之間的關系,成本低且數據信息反映了零部件的真實運行環境,是一種較理想的壽命預測方法。
基于此,在以上研究的基礎上,以零部件失效數據和歷史服役工況數據為基礎,聯合威布爾分布和多元回歸分析模型來評估廢舊零部件的剩余使用壽命。
1 廢舊零部件剩余使用壽命評估模型
基于零部件失效數據和歷史服役工況數據的廢舊零部件剩余使用壽命評估過程可用以下公式進行描述[11]:

式中:LR代表零部件的剩余使用壽命,LM代表零部件的平均使用壽命,LA代表零部件的實際使用壽命。
1.1 平均使用壽命LM
LM反映了零部件在穩定工況下的正常運行時間,可以通過零部件的失效數據建立其威布爾分布模型計算得出。由于兩參數的威布爾分布具有廣泛的應用和靈活性[12],因此,采用兩參數的威布爾分布模型,利用零部件的失效數據來評估其平均使用壽命,計算公式如下所示。
平均使用壽命為:
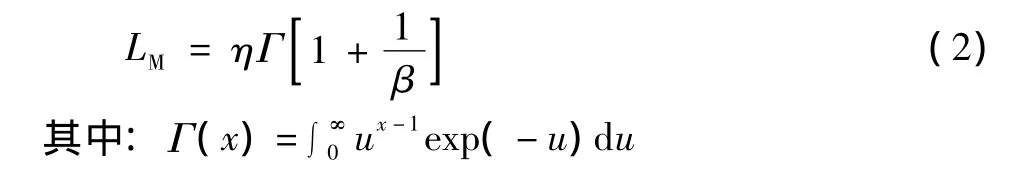
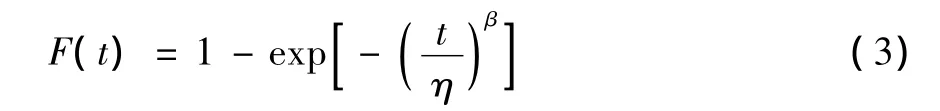
式中:η表示尺度參數;β表示形狀參數,指的是失效模式。如圖1所示,當0<β<1時,表明是早期失效期,失效率嚴格遞減;當β=1時,表明是偶然失效期,失效率不變;β>1時,表明是耗損失效期,失效率嚴格遞增。
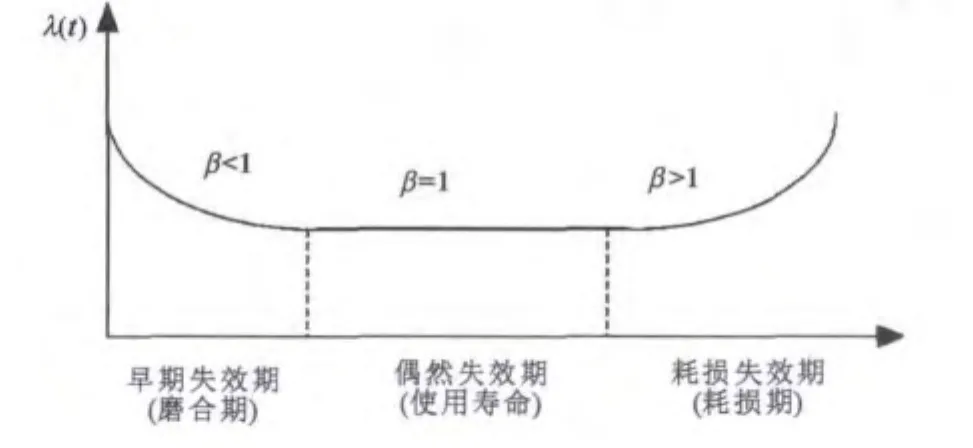
圖1 威布爾模型參數
威布爾分布的失效分布函數為:
在以上兩參數的威布爾分布模型中,參數η和β的估計是關鍵。數據樣本是參數估計的基礎,失效數據有效地反映了零部件在運行過程中的壽命變化,是較理想的參數估計數據樣本。失效數據的主要來源有[13]:試驗數據和現場數據。與試驗數據相比,現場數據更能真實反映零部件的運行環境。現場數據通常是截尾的,取決于數據收集的時間窗口,有可能在數據收集期內零部件還沒有發生失效,這一部分數據在失效數據統計表中也需要體現出來。以某型號零部件失效數據表為例,如表1所示。

表1 某型號零部件失效數據表
目前常用的參數估計法主要有[14]:圖估計法、極大似然估計法和最小二乘估計法。其中,由于最小二乘估計法計算量小、計算簡單直觀以及能有效實現數據的線性化處理等特點,是一種較理想的威布爾分布參數估計方法[15],其具體計算過程如下所示。
將式 (3)左右變形,取自然對數可得:

對于式 (5),回歸系數A和B的最小二乘解為:

由此得到的參數估計為:

在最小二乘參數估計過程中,為了提高回歸系數估計值的精度,關鍵是要提高經驗分布函數的精度,傳統的經驗分布函數計算方法是通過近似中位秩公式(8)得到,誤差較大。

式中:i為失效零部件的順序號,n為樣本總容量。
平均秩次法通過數據樣本估算出所有可能的秩次,求出平均秩次,從而得到經驗分布函數,有效地提高了參數估計的精度[16],平均秩的增量計算如下:
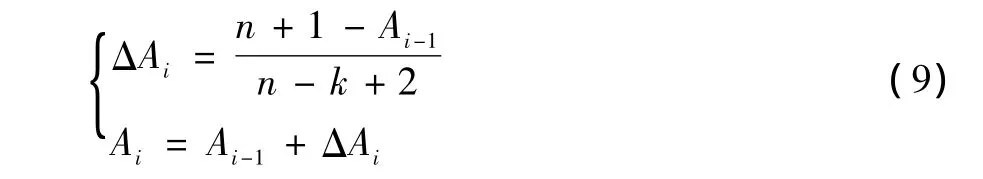
式中:n為樣本總容量;i為失效零部件的順序號;k為零部件的排列順序號,按照失效時間和刪失時間的

利用最小二乘法,將零部件發生失效的時間和利用公式 (10)計算出來的經驗分布函數擬合威布爾分布模型的回歸直線,從而確定尺度參數η和形狀參數β。
1.2 實際使用壽命LA
LA反映了零部件在動態工況下的實際運行時間,對于同一產品來說,服役的工況不一樣,LA的值也不一樣,因此,LA是一個隨著產品服役環境而變化的動態值。針對該問題,以多元回歸分析模型為基礎,廢舊零部件歷史運行工況數據為輸入,該工況條件下的實際使用壽命為輸出,建立零部件的運行工況數據和實際使用壽命之間的關系,從而預測在特定工況條件下,廢舊零部件的實際使用壽命。其預測模型如下所示:
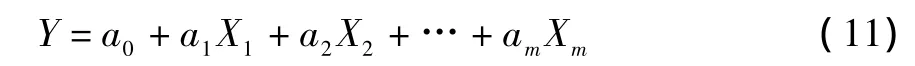
式中:a0,a1,…,am為待估計的回歸系數;X1,X2,…,Xm為廢舊零部件的運行工況數據;Y為該工況數據下廢舊零部件的實際使用壽命。
2 案例分析
目前,全國役齡10年以上的傳統機床超過200萬臺,為了提高機床的效率和精度,需對廢舊機床進行升級改造[17]。電機作為機床重要的組成零部件,是機床電氣系統升級改造的主要對象之一。機床升級改造所替換下的廢舊電機還可用于其他用途。然而廢舊電機是否具有剩余使用壽命,其剩余使用壽命能否維持下一個壽命周期決定了運行的可靠性。在此,以廢舊機床電機的剩余使用壽命評估為例對以上模型進大小排序;Ai為失效零部件的平均秩次。
將Ai代入公式 (8),可得行驗證。
(1)電機平均壽命LM
電機的失效數據來源于現場數據,如表2所示。
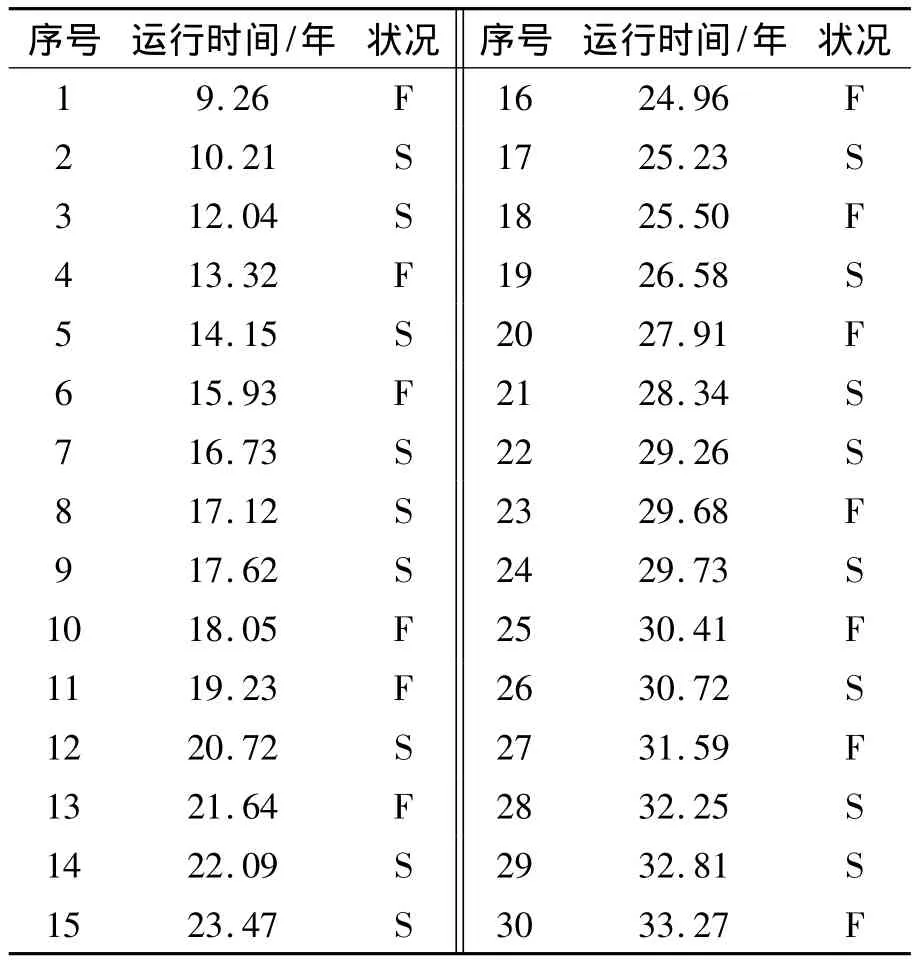
表2 電機的失效數據表
表2中的數據包括失效數據和刪失數據。去掉刪失數據,將發生失效的電機按照失效時間順序重新排序,建立威布爾分布模型,由式 (9)和 (10)分別計算出失效電機的平均秩次和經驗分布函數值,如表3中的第3和第4列。
以4號電機的經驗分布函數值計算為例。
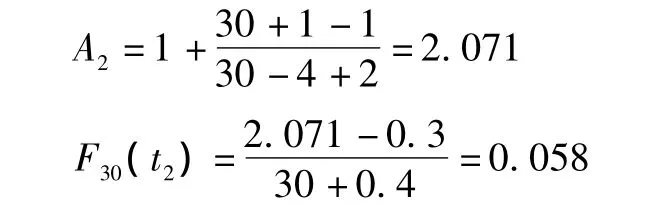
式中:30為樣本總數。
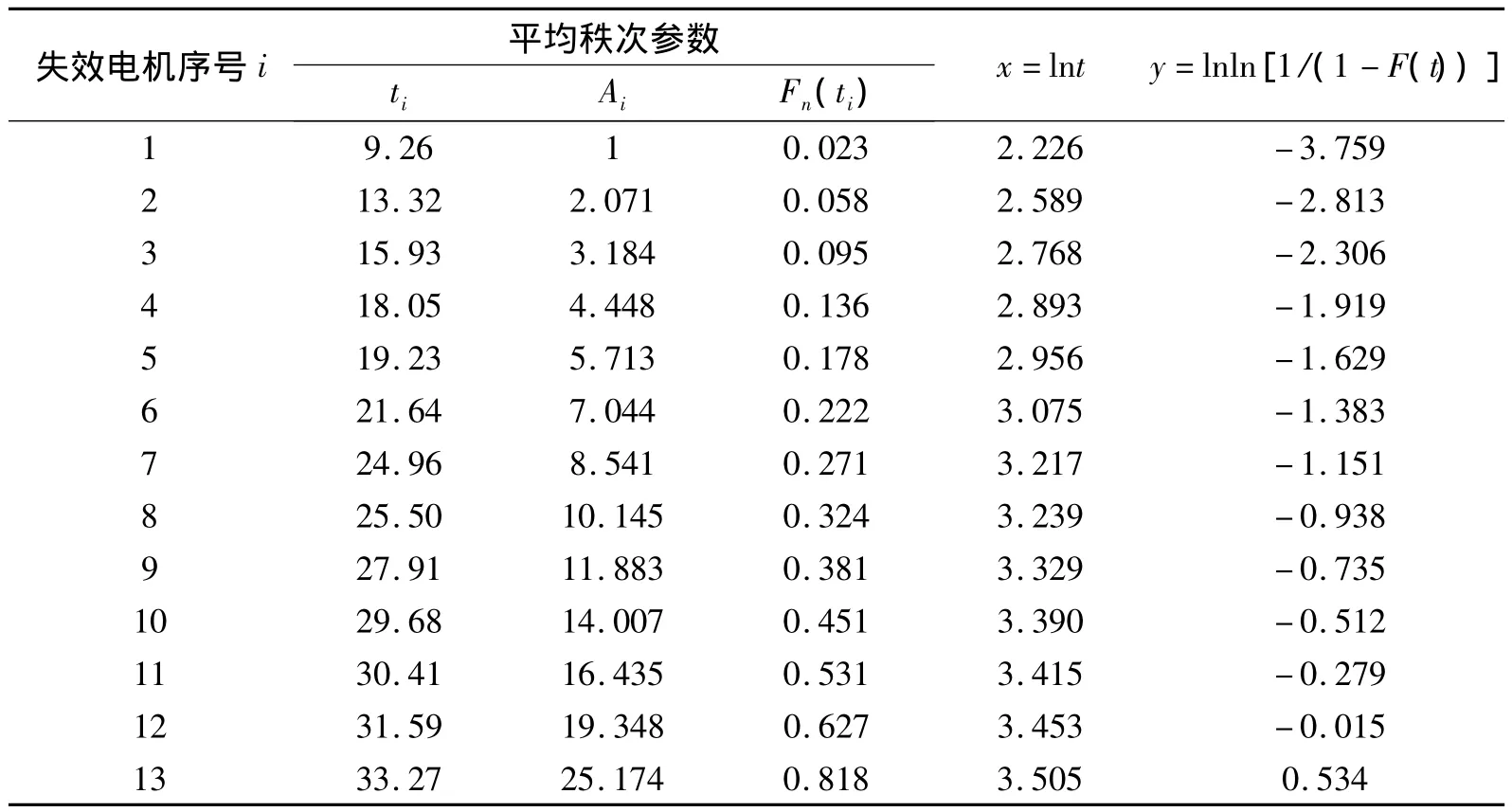
表3 經驗分布函數計算表
將表3中第5列和第6列的x和y值代入式(6),得到A=3.069,B=-10.757。再由式 (7)可計算出威布爾分布參數:β=3.069,η=33.277,將β和η代入式 (2)可得電機平均使用壽命為:
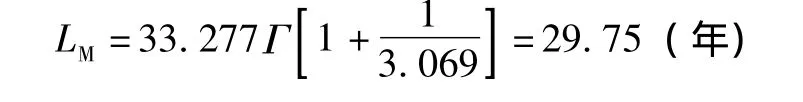
(2)電機實際壽命LA
選取電機的轉速 (X1)、功率 (X2)以及電流(X3)等工況參數作為輸入,電機在該工況條件下的實際運行時間為輸出,建立運行工況參數與實際使用壽命之間的回歸模型。數據樣本如表4所示。
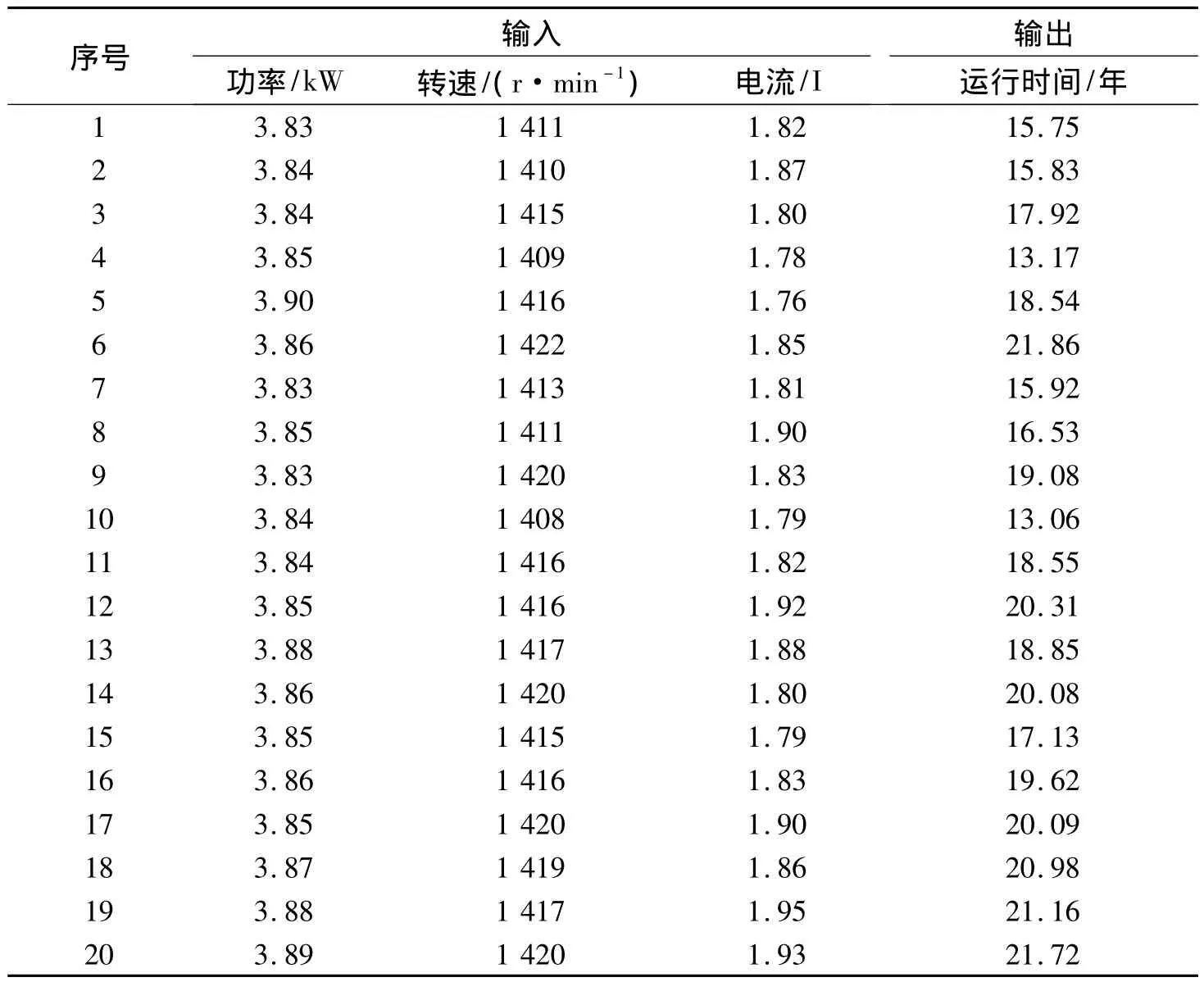
表4 數據樣本
以上表中數據樣本為基礎,應用SPSS17.0統計軟件進行分析。分析結果如表5和表6所示。由表5可知:統計量F=75.468大于在0.001顯著水平的值,說明回歸方程是極顯著的;相伴概率P<0.001,說明功率、轉速和電流與運行時間存在線性關系;回歸方程相關系數R=0.966,決定系數R2=0.934>0.85,說明回歸方程對樣本點的擬合效果很好。根據表6中的回歸系數顯著性檢驗建立功率、轉速和電流與運行時間之間的多元回歸方程:
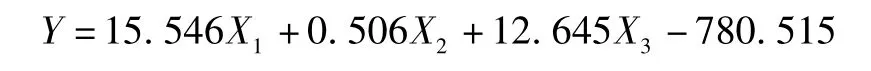

表5 方差分析
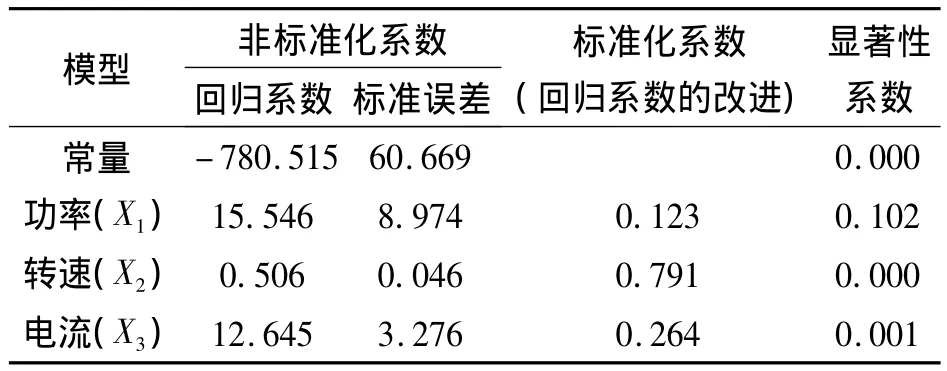
表6 回歸系數及顯著性檢驗
基于以上預測模型,通過輸入電機的運行工況數據,可以實時預測電機的實際使用壽命;結合電機的平均使用壽命,即可得出電機的剩余使用壽命,如表7所示。根據剩余使用壽命的值可以合理確定電機的其他使用用途,保證電機的利用價值最大化。

表7 電機剩余使用壽命
3 結論
廢舊零部件剩余使用壽命評估的準確性決定了其再利用的潛力。以零部件失效數據和歷史服役工況數據為基礎建立了廢舊零部件剩余使用壽命評估模型,與傳統零部件剩余使用壽命評估方法相比,該模型充分考慮了產品的實際運行環境。案例分析表明:該模型能較好地表達出廢舊零部件的失效數據、歷史運行工況數據和剩余使用壽命之間的關系,可為廢舊零部件剩余使用壽命評估的研究和應用提供一種基礎支持。
[1]董麗虹,徐濱士,董世運,等.金屬磁記憶技術用于再制造毛坯壽命評估初探[J].中國表面工程,2010,23(2):106-111.
[2]DATTOMA V,GIANCANE S,NOBILE R,et al.Fatigue Life Prediction under Variable Loading Based on a New Non-linear Continuum Damage Mechanics Model[J].International Journal of Fatigue,2006,28(2):89 -95.
[3]MAKKONEN M.Predicting the Total Fatigue Life in Metals[J].International Journal of Fatigue,2009,31(7):1163 -1175.
[4]MOHANTY J R,VERMA B B,RAY P K,et al.Application of Artificial Neural Network for Fatigue Life Prediction under Interspersed Mode-I Spike Overload[J].Journal of Testing and Evaluation,2010,38(2):96 -101.
[5]KIM Y H,SONG J H,PARK J H.An Expert System for Fatigue Life Prediction Under Variable Loading[J].Expert Systems with Applications,2009(3):4996 -5008.
[6]吳學仁,劉建中.基于小裂紋理論的航空材料疲勞全壽命預測[J].航空學報,2006,27(2):219 -226.
[7]呂凱波,劉混舉.基于有限元法的機械疲勞壽命預測方法的研究[J].機械工程與自動化,2008(6):113-114.
[8]張景柱,徐誠,胡良明,等.基于ADAMS的操縱摩擦件壽命仿真預測方法[J].機械科學與技術,2007,26(6):767-769.
[9]BUKKAPATNAM S T S,SADANANDA K.A Genetic Algorithm for Unified Approach-based Predictive Modeling of Fatigue Crack Growth[J].International Journal of Fatigue,2005,27(10/11/12):1354 -1359.
[10]LI J,MU X D,ZHENG S,et al.Research on Lifetime Grey Prediction of Electronic Equipment Based on Improved Genetic Algorithm[C]//International Conference on Advanced Computer Control.Singapore.Los Alamitos:IEEE Computer Society,2009:493 -496.
[11]ANITYASARI M,KAEBERNICK H.A Concept of Reliability Evaluation for Reuse and Remanufacturing[J].International Journal of Sustainable Manufacturing,2008,1(1):3-17.
[12]胡昊磊,左洪福,任淑紅.基于隨機過程的航空發動機性能可靠性預測[J].科技信息,2009(29):17-18.
[13]鄒瑤,符萌,左飛.基于競爭失效模式的發送器和接收器的故障分析[J].鐵路計算機應用,2011,20(6):15-18.
[14]毛昭勇,宋保維,李正,等.基于遺傳算法的最大似然參數優化估計[J].機械強度,2006,28(1):79 -82.
[15]于曉紅,張來斌,王朝暉,等.基于新的威布爾分布參數估計法的設備壽命可靠性分析[J].機械強度,2007,29(6):932-936.
[16]王博,劉媛,洪其麟,等.對軍用航空發動機可靠性參數體系選擇和指標確定的探討[J].燃氣渦輪試驗與研究,2003,16(2):38 -42.
[17]徐濱士.再制造工程的現狀與前沿[J].材料熱處理學報,2010,31(1):10-14.

