含多運動副間隙機構動態特性研究*

丁 鍵，趙 宇，吳洪濤，陳 柏，朱留存，謝亞非

(1.南京航空航天大學 機電學院，南京 210016；2.常州精銳自動化裝備技術有限公司，江蘇 常州 213032)

含多運動副間隙機構動態特性研究*

丁 鍵1，趙 宇1，吳洪濤1，陳 柏1，朱留存2，謝亞非2

(1.南京航空航天大學 機電學院，南京 210016；2.常州精銳自動化裝備技術有限公司，江蘇 常州 213032)

為了研究運動副間隙對機構動態特性的影響，文章基于一種非線性接觸碰撞力模型和修正了的庫侖摩擦力模型，描述含間隙運動副內關節元素的接觸碰撞作用，并在動力學仿真軟件ADAMS環境中，以含運動副間隙曲柄滑塊機構為例，對其進行動力學仿真。分別考慮間隙尺寸、間隙位置和類型、曲柄轉速以及間隙數目對機構動態特性的影響，拓展了間隙碰撞動力學建模與含間隙機構動力學仿真的研究，為機構的設計提供了重要的參考依據，有利于工程實際應用。

多運動副間隙；接觸碰撞；摩擦；動態特性

0 引言

在傳統的機械多體系統動力學分析中，運動副通常是被假設為理想的，然而工程實際中，運動副中的間隙是不可避免的。隨著精密機械和宇航工程的發展，含間隙機構動力學成為該領域迫切需要解決的關鍵問題之一[1-2]。文章以曲柄滑塊機構為例，從轉動副、移動副間隙碰撞模型的正確描述、碰撞力的準確建模入手，在ADAMS環境中仿真運動副元素間的非線性碰撞力作用，研究間隙對機構的動力學特性的影響。

1 含間隙機構動力學建模

1.1 運動副間隙的矢量模型

理想轉動關節軸和軸承的中心由旋轉副連接并重合，間隙使得機構獲得平面內兩個徑向移動自由度。如圖1所示，軸和軸承未發生接觸變形時，間隙矢量的大小被限制在以軸承中心為圓心，以軸承半徑RB和軸半徑RJ之差c為半徑的間隙圓內，即：

c=RB-RJ

(1)

圖1 轉動副間隙示意圖

圖2 轉動副間隙矢量圖

(2)

當軸和軸承發生接觸變形時，如圖3所示，由此引起的接觸形變量δ為間隙矢量大小e和間隙大小c之差：

δ=e-c

(3)

圖3 軸和軸承接觸變形

國內外關于移動副間隙的動力學研究文獻[4-6]相對較少。滑塊和導軌被看成兩個碰撞體，滑塊在導軌內存在如圖4所示的四種典型接觸方式: 圖4a自由飛行; 圖4b滑塊的一條棱邊和導軌表面接觸; 圖4c滑塊一個側面和導軌表面接觸; 圖4d滑塊相對棱角和導軌表面接觸。

圖4 滑塊與導軌表面接觸狀態

(4)

1.2 運動副間隙的接觸碰撞力模型

含間隙機構動力學分析在很大程度上取決于接觸碰撞力的建模。Lankarani-Nikravesh(L-N)模型[7]在通用Hertz接觸力表達式的基礎上，考慮碰撞過程中由材料阻尼引起的能量損失行為，其表達式為：

(5)

(6)

其中剛度系數Kn和阻尼系數Dmod分別為：

(7)

(8)

式(7)中復合楊氏模量E*關于軸承、軸的楊氏模量EB、EJ和泊松比VB、VJ的函數關系為：

(9)

圖5 移動副間隙矢量模型

移動副間隙接觸力模型主要取決于滑塊和導軌的接觸方式。當滑塊兩個相鄰的拐角接觸導軌表面，如圖4c產生面接觸時的情形，Lankarani于1988年提出了該型接觸碰撞中彈性力FN關于接觸長度a、接觸形變δ和材料固有屬性σi、σj的線性模型表達式為：

(10)

當滑塊產生角接觸，即如圖4(b)、(d)時，假設滑塊拐角處有一個小的曲率半徑,則接觸力產生于弧面和平面之間，Goldsmith通過實驗測得球體i和平面j在碰撞過程中的接觸碰撞彈性力為關于球體半徑Ri、材料屬性σi、σj和接觸形變的函數：

(11)

在這里用于近似計算滑塊和導軌角接觸時的接觸彈性力，相應的阻尼系數可由式(8)計算得到。

1.3 運動副間隙的摩擦力模型

本文所研究機構中的摩擦不考慮潤滑作用，即干摩擦。最為著名的摩擦力模型[9]是Coulomb摩擦模型，較為廣泛地使用于沖擊或碰撞中的摩擦行為。為了更加精準地描述物體之間的摩擦行為，以及物體相對低速情況下易發生的粘滯-微滑現象，本文采用修正[10]了的Coulomb摩擦力模型，其計算表達式為：

(12)

式(12)中動態摩擦系數μ(vt)的函數表達式為：

(13)

式中vt為切向滑動速度，μd為動摩擦系數，μs為靜摩擦系數，vs為靜摩擦臨界速度，vd為最大動摩擦臨界速度，其函數曲線如圖6所示。

圖6 動態摩擦系數隨切向滑動速度曲線

2 含間隙機構動態特性研究

2.1 機構幾何參數與質量特性

含間隙曲柄滑塊機構如圖7所示，曲柄-連桿轉動副A處、連桿-滑塊轉動副B處以及滑塊-導軌移動副C處可以設置間隙。機構參數如下：曲柄長度l1=50mm、質量m1=0.58kg、轉動慣量J1=122.86kg·mm2；連桿長度l2=120mm、質量m2=0.94kg、轉動慣量J2=141.27kg·mm2；滑塊質量m3=0.98kg、轉動慣量J3=245.74kg·mm2，恢復系數Ce=0.9，楊氏模量E=207GPa，泊松比ν=0.29。

圖7 含間隙曲柄滑塊機構

2.2 動態仿真分析

為研究運動副間隙對機構的運動特性影響，取間隙c=0.5mm，曲柄轉速為ω=200rpm，進行動力學仿真，分別僅考慮機構在運動副A,B和C處存在間隙，系統穩定后的兩個完整周期內，含間隙機構和理想機構的滑塊運動特性曲線對比如圖8～10所示。

通過上述對比結果可知，間隙對滑塊的位移幾乎沒有影響，對滑塊速度影響較小，而對滑塊加速度影響最大。圖8和圖9表明，轉動副A處間隙對滑塊運動的影響相對B處間隙的影響要大，這說明間隙離曲柄越近對機構的影響越大，這與文獻[11]的實驗結論一致。對比圖8～10發現，移動副間隙對滑塊運動的影響要比轉動副間隙的影響更明顯，這是由于滑塊在導軌內的運動狀態相對軸在軸承內的運動狀態較復雜導致的。

進而研究間隙尺寸對機構動力學性能的影響，以運動副B存在間隙為例，取間隙分別為0.5mm，0.2mm以及0.05mm，在同一轉速200rpm下進行動力學仿真，將其動態特性曲線與理想機構作對比如圖11～13所示，圖中a、b、c和d分別描述系統穩定后的兩個完整周期內，滑塊加速度、曲柄驅動扭矩、Poincaré 映射(滑塊加速度關于速度的函數曲線，其光滑程度表示系統的穩定程度)和第一個周期內間隙關節碰撞力曲線。

對比發現，間隙越小，表征系統動態特性的曲線越光滑，即系統動態特性越趨于理想機構，這與文獻[11]的實驗結果一致；對比圖11～13中d可見，間隙的存在使得關節接觸碰撞力大幅提高并且在系統穩定前呈高頻振蕩，間隙越小，碰撞力越小，但振蕩頻率越高，而系統建立穩定越快。

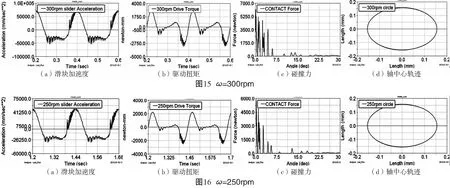
其次研究曲柄轉速對含間隙機構動力學性能的影響。仍以運動副B處間隙為例，取間隙大小C=0.2mm，分別設置曲柄轉速為350rpm、300rpm和250rpm對機構進行動力學仿真，結果如圖14～16所示，a、b、d分別為系統穩定后兩個完整周期內的滑塊加速度、曲柄驅動扭矩、軸中心相對軸承參考坐標系的運動軌跡曲線，圖14～16中c為系統穩定前間隙關節碰撞力曲線。

對比圖14～16發現，曲柄轉速越高，滑塊加速度、曲柄扭矩以及碰撞力曲線振蕩越厲害并且幅值越大，系統到達穩定的時間越長，圖14～16中d表明系統穩定后，在沒有外部沖擊載荷的情況下，軸總是緊貼軸承內圈表面做圓周運動的，這些結論也都與文獻[11]的實驗結果相吻合。

最后，考慮機構在轉動副B處和移動副C處同時存在間隙C=0.2mm，曲柄轉速200rpm的情況下，對機構進行動力學仿真。取系統穩定后的兩個完整周期作研究，機構動態特性參數曲線如圖17所示。圖17a、b分別為滑塊加速度和曲柄驅動扭矩曲線，圖17c、d分別為軸中心在軸承參考坐標系中和滑塊中心在導軌參考坐標系中的運動軌跡曲線。

由圖17a、b可見，本文研究的含多運動副間隙機構總體運行平穩，但滑塊運動到上、下死點位置時，機構振動明顯，表現出機構的局部混沌[12]現象，且相比只含轉動副或移動副的情況要劇烈的多，顯然是轉動副和移動副間隙之間產生相互耦合影響。圖17c、d說明隨著機構的運行，間隙鉸元素間可以分為三種狀態：軸(滑塊)沿軸承(導軌)內壁滑移、自由飛行和反彈碰撞。

3 結論

機構運行過程中，間隙不可避免地存在于各活動鉸接處，并使得機構的動態特性偏離理想機構。文章基于一種非線性混合碰撞力模型和改進了的Coulomb摩擦力模型，以曲柄滑塊機構為對象，在動力學仿真軟件ADAMS中對其進行動態特性分析。所得結論與國外早前的實驗研究結果吻合，說明了本文所采用研究方法的可行性，可用于較好地預測含間隙機構動力學行為特征，有一定的工程指導價值。

[1] Megahed, S.M., Haroun, A.F.: Analysis of the dynamic behavioral performance of mechanical systems with multi-clearance joints. J. Comput. Nonlinear Dyn. , 2011(7)：1-11.

[2] Khulief, Y.A.: Modeling of impact in multibody systems:An overview. J. Comput. Nonlinear Dyn.8, 021012 ，2013：4-7.

[3] Flores, P., Lankarani, H.M.: Dynamic response of multi-body systems with multiple clearance joints. J. Comput.Nonlinear Dyn.7(3), 031003 (2012)：2-3.

[4] Flores P, Leine R, Glocker C. Modeling and analysis of planar rigid multibody systems with translational clearance joints based on the non-smooth dynamics approach[J]. Multibody System Dynamics. 2010,23: 65-190.

[5] Flores P, Ambrósio J, Claro JCP, Lankarani HM. Translational Joints with Clearance in Rigid Multibody Systems[J]. Journal of Computational and Nonlinear Dynamics. 2008(3):1-10.

[6] Muvengei, O., Kihiu, J., Ikua, B.: Dynamic analysis of multi-body mechanical systems with imperfect kinematic joints: a literature survey and review. Sustain. Res. Innov.Proc., 2011(3)：61-76.

[7] Lankarani HM, Nikravesh PE. A Cont act Force Model With Hysteresis Damping for Impact Analysis of Multibody Systems[J]. Journal of Mechanical Design.1990,112:369-376.

[8] 白爭鋒.考慮鉸間間隙的機構動力學特性研究[D].哈爾濱：哈爾濱工業大學，2011.

[9] 溫詩鑄，黃平. 摩擦學原理( 第3 版)[M].北京：清華大學出版社，2008.

[10] MSC Software, M.Sc. ADAMS?, Release R3, Help System(2008).

[11] Flores P. Dynamic Analysis of Mechanical Systems with Imperfect Kinematic Joints[D]. Portugal: Universidade Do Minho Ph.D thesis, 2004：185-204.

[12] 胡海巖.分段線性系統動力學的非光滑分析[J]. 力學學報，1996,28(4)：483-488.

(編輯 李秀敏)

Dynamic Characteristics of Mechanisms with Multi-clearance Joints

DING Jian1,ZHAO Yu1,WU Hong-tao1, CHEN bai1,ZHU Liu-cun2, XIE Ya-fei2

(1. College of Mechatronics, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China；2. Changzhou Jingrui Automatic Equipment and Technology Co. , Ltd , Changzhou Jiangsu 213032, China)

In order to study the dynamic characteristics of mechanisms with joint clearance, the work based on a nonlinear contact model and an improved Coulomb friction model. In the environment of dynamics simulation software ADAMS, the slider-crank mechanism is chosen as an example to be demonstrated. Consider the influence of dynamic performance due to clearance size, clearance type and clearance position, rotation speed of crank and clearance numbers respectively, which expands the dynamics modeling of mechanism with clearance, and gives the basis of mechanism design.

multi-clearance joints; contact; friction; dynamic characteristic

1001-2265(2014)05-0009-05

10.13462/j.cnki.mmtamt.2014.05.003

2013-09-10;

2013-09-25

國家自然基金(51375230)；江蘇省科技支撐計劃(BE2012052)

丁鍵(1987—)，男，江蘇鹽城人，南京航空航天大學碩士研究生，研究方向為多體系統，(E-mail)nuaa_ding@163.com。

TH112；TG65

A