交換環(huán)的素譜與極大譜的連通性

謝國(guó)根

(銅陵學(xué)院數(shù)學(xué)與計(jì)算機(jī)學(xué)院,安徽 銅陵 244000)

交換環(huán)的素譜與極大譜的連通性

謝國(guó)根

(銅陵學(xué)院數(shù)學(xué)與計(jì)算機(jī)學(xué)院,安徽 銅陵 244000)

試圖刻劃交換環(huán)的素譜和極大譜的連通分支,為此本文討論了交換環(huán)的本原冪等元與素譜以及極大譜的連通分支的關(guān)系.證明了若e為本原冪等元,則D(e)為SpecA的連通分支.類(lèi)似地,若e為A的本原冪等元且Nil(A)=Rad(A),則為maxA的連通分支.

素譜;極大譜;連通性;本原冪等元

1 引言

交換環(huán)的素譜和極大譜是代數(shù)幾何的重要研究對(duì)象之一,已知交換環(huán)A的素譜是連通的當(dāng)且僅當(dāng)A中只有0和1是冪等元.由于對(duì)任意拓?fù)淇臻g,它的連通分支構(gòu)成它的覆蓋.所以若交換環(huán)的素譜不連通,可以進(jìn)一步去研究它的連通分支.因此不同于文獻(xiàn)[1-3]討論素譜整體的的連通性,本文主要研究其連通分支,首先討論了素譜的連通分支與交換環(huán)的本原冪等元的關(guān)系,并隨后討論了極大譜上的相應(yīng)情形.

2 拓?fù)渖系念A(yù)備知識(shí)

定義 2.1稱(chēng)映射f:X→ Y是連續(xù)的(X,Y為拓?fù)淇臻g),若Y的任意一開(kāi)集的原像是X的開(kāi)集,或等價(jià)地,Y的任意一閉集的原像是X的閉集.

定義 2.2拓?fù)淇臻gX稱(chēng)為連通的,如果它不能分解為兩個(gè)非空不相交開(kāi)集的并(或者等價(jià)地,它不能分解為兩個(gè)非空不相交閉集的并).

引理 2.1連通空間在連續(xù)映射下的像也是連通的.

定義 2.3拓?fù)淇臻gX的一個(gè)子集稱(chēng)為X的連通分支,如果它是連通的,并且不是X的其他連通子集的真子集.

引理 2.2X的每個(gè)非空連通子集包含在唯一的一個(gè)連通分支中.

注 2.1X中任意一點(diǎn)x作為子空間是連通的,因此x包含在唯一的連通分支中.換句話(huà)說(shuō),X的所有連通分支構(gòu)成X的覆蓋,并且它們兩兩不相交.

引理 2.3連通分支是閉集.

3 素譜的連通分支與本原冪等元的關(guān)系

注 3.1若A為交換環(huán),記SpecA為A的所有素理想的集合.記V(a)={p∈SpecA|a?p}.對(duì)任意f∈A,(f)表示fA,記

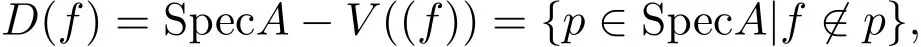
則SpecA以V(a)為閉子集構(gòu)成拓?fù)淇臻g.

引理 3.1令A(yù)是交換環(huán),則下列條件等價(jià):

(i)SpecA是連通的.

(ii)A中只有0和1是冪等元.

證明見(jiàn)文獻(xiàn)[5]命題1.3.1.

注 3.2由文獻(xiàn)[5]命題1.3.1的證明過(guò)程可知,對(duì)任意A中的冪等元e,

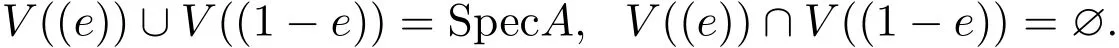
引理 3.2設(shè) e為交換環(huán) A的冪等元,做環(huán)同態(tài) ?:A→ Ae使得 ?(r)=re,r∈A,則f:SpecAe→SpecA(其中f(q)=??1(q),q∈SpecAe)連續(xù),且Im f=D(e).

證明f的連續(xù)性可由文獻(xiàn)[5]中的命題1.2.5得到,下證Im f=D(e).

對(duì)任意 q∈SpecAe,由 q是素理想,e是 Ae的單位元可知,e/∈q,所以 e/∈??1(q),即Im f?D(e).

反之,對(duì)p∈SpecA且e/∈p,由V((e))∪V((1?e))=SpecA知,(1?e)?p,所以

顯然,p∩(e)為Ae的素理想.

易得??1(p∩(e))?p,且若x∈??1(p∩(e)),即xe∈p∩(e).又x=xe+x(1?e),所以

故??1(p∩(e))=p,即Im f?D(e).

定理 3.1設(shè)e為交換環(huán)A的本原冪等元,則D(e)為SpecA的連通分支.

證明因?yàn)閑為交換環(huán)A的本原冪等元,所以Ae中的冪等元只有0和e.由引理3.1知SpecAe是連通的.則由引理3.2知D(e)為連通空間SpecAe在連續(xù)映射下的像,則由引理2.1知D(e)為SpecA的連通子集.

由引理2.2,可設(shè)F是包含D(e)的連通分支,且由引理2.3知,F是閉集.再由引理3.1的注記知D(e)=V((1?e)),故D(e)也是閉集.由D(e)?F得,

且D(e)∩(F∩V((e)))=?,由F的連通性知F∩V((e))=?,即F=D(e).

所以D(e)是SpecA的連通分支.

由文獻(xiàn)[6]中第7節(jié)的練習(xí)7,練習(xí)8可得到如下引理:

引理 3.3設(shè)R是由一切連續(xù)函數(shù)f:構(gòu)成的環(huán).則R的每個(gè)冪等元都不是本原的.

注 3.3由引理3.3知,對(duì)任意交換環(huán)A,SpecA的連通分支未必能寫(xiě)成D(e)的形式(其中e是A的本原冪等元).所以定理3.1的逆命題不成立.

4 極大譜的連通分支與本原冪等元的關(guān)系

一些記號(hào)及說(shuō)明若A為交換環(huán),記maxA為A的所有極大理想的集合.記A的所有素理想的交為Nil(A),記A的所有極大理想的交為Rad(A).

易得:

(2)如果{ai}(i∈A)是A的理想的任意集合,則

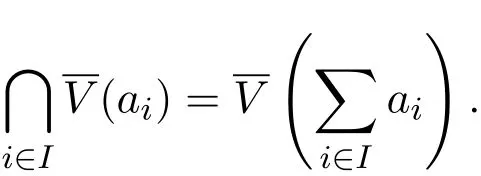
(3)如果a,b是A的兩個(gè)理想,則

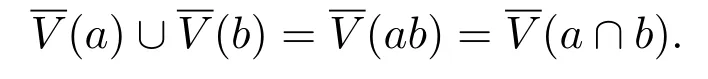
對(duì)任意f∈A,(f)表示fA,記

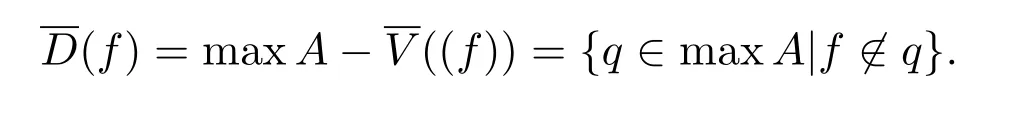
引理 4.1設(shè)a是交換環(huán)A的詣零理想,=A/a.則若x∈A使得是的冪等元,則存在A的冪等元e,使得

證明見(jiàn)文獻(xiàn)[8]定理1.8.5.

引理 4.2令A(yù)是交換環(huán),且Nil(A)=Rad(A),則下列條件等價(jià):

(i)maxA是連通的.

(ii)A中只有0和1是冪等元.

證明(i)?(ii)設(shè)e為A的冪等元,則e(1?e)=0.所以

因此a,b為A的真理想,且

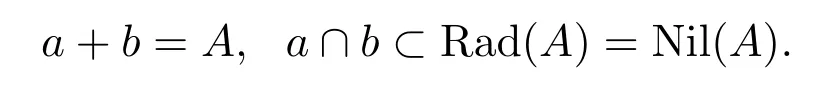
注 4.1由希爾伯特零點(diǎn)定理 (文獻(xiàn) [9]定理 1.6)可知,若 A為有限生成 K 代數(shù),則Nil(A)=Rad(A),所以這里要求Nil(A)=Rad(A)并不是一個(gè)相當(dāng)苛刻的條件.有限生成K代數(shù)在代數(shù)幾何中是一類(lèi)相當(dāng)重要的環(huán).

引理 4.3若?:A→B為交換環(huán)A,B的滿(mǎn)同態(tài),則對(duì)任意q∈maxB,有??1(q)∈maxA,且由此誘導(dǎo)的映射f:maxB→maxA(其中f(q)=??1(q))連續(xù).

證明由于是?滿(mǎn)同態(tài),所以在A中包含ker?的理想和B中的理想一一保序?qū)?yīng).因此??1(q)∈maxA.

再由對(duì)任意A的理想a,及q∈maxB,

引理 4.4設(shè) e為交換環(huán)A的冪等元,做環(huán)同態(tài) ?:A→Ae使得?(r)=re,r∈A,

則f:maxAe→maxA(其中f(q)=??1(q),q∈maxAe)連續(xù),且Im

證明f的連續(xù)性可由引理4.3得到,下證

僅需證明

余下的證明與引理3.2類(lèi)似.

再由?是滿(mǎn)同態(tài),所以A中包含ker?的理想和Ae中的理想一一保序?qū)?yīng).因此

定理 4.1設(shè)e為交換環(huán)A的本原冪等元,且Nil(A)=Rad(A),則(e)為maxA的連通分支.

證明僅需說(shuō)明Nil(A)=Rad(A)?Nil(Ae)=Rad(Ae),余下證明與定理3.1類(lèi)似.

由引理 4.4的證明過(guò)程可知 q∈maxA,e/∈q? q∩Ae∈maxAe.另外顯然有 q∈maxA,e∈q?Ae?q.所以對(duì)于任意x∈Ae,若x∈Rad(Ae),則有x∈Rad(A)=Nil(A).故x冪零.因此x∈Nil(Ae),即Nil(Ae)=Rad(Ae).

5 總結(jié)

本文主要是利用本原冪等元來(lái)刻畫(huà)素譜和極大譜的連通分支,但是由引理3.3知,并不是所有的連通分支都可以用本原冪等元來(lái)刻畫(huà).所以認(rèn)為有以下問(wèn)題是值得進(jìn)一步研究的：

(1)能否給出素譜和極大譜的連通分支的一般形式的刻畫(huà);

(2)如(1)不能實(shí)現(xiàn),那么能否對(duì)一些特殊的環(huán)(如引理3.3中提到的環(huán))刻畫(huà)出它所有的連通分支.

[1]馮良貴.環(huán)的素譜的若干注記(英文)[J].數(shù)學(xué)研究,2001(1):27-30.

[2]王江.交換環(huán)的素譜空間的連通性[J].山東師大學(xué)報(bào):自然科學(xué)版,1989(2):16-22.

[3]陳剛.一個(gè)特征標(biāo)環(huán)素譜的連通性[J].數(shù)學(xué)雜志,2005(2):30-34.

[4]高恩偉,張金霞.素理想P在F中分解[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2012(5):569-572.

[5]Fu L.Algebraic Geometry[M].北京:清華大學(xué)出版社,2006.

[6]Anderson F W,Fuller K R.Rings and Categories of Modules[M].New York:Spring-verlag,1974.

[7]尤承業(yè).基礎(chǔ)拓?fù)鋵W(xué)[M].北京:北京大學(xué)出版社,1997.

[8]王芳貴.交換環(huán)與星形算子理論[M].北京:科學(xué)出版社,2006.

[9]Iitaka S.Algebraic Geometry:An Introduction to Birational Geometry of Algebraic Varieties[M].New York: Spring-Verlag,1982.

Connectedness of the prime spectrum and the maximal spectrum of a commutative ring

Xie Guogen
(College of Mathematics and Computer,Tongling University,Tongling 244000,China)

The main purpose of this paper is trying to character connected components of the prime spectrum and the maximal spectrum of a commutative ring.To this aim,the relationship between primitive idempotents and connected components of the prime spectrum and the maximal spectrum is discussed.It is proved that D(e)is a connected component of SpecA if e is a primitive idempotent of A.Analogously,(e)is a connected component of maxA if e is a primitive idempotent of A and Nil(A)=Rad(A)

prime spectrum,maximal spectrum,connectedness,primitive idempotent

O178

A

1008-5513(2014)02-0216-05

10.3969/j.issn.1008-5513.2014.02.014

2013-06-09.

謝國(guó)根(1985-),碩士生,研究方向:環(huán)論與代數(shù)表示論.

2010 MSC:16D10