刻畫排列的連通分支
高犇
(太原理工大學數學學院,山西 太原 030024)
刻畫排列的連通分支
高犇
(太原理工大學數學學院,山西 太原 030024)
應用柱代數分解算法和簡化的胞腔相鄰算法,得到一個刻畫R3中由n個緊半代數集所組成排列連通分支的算法.
連通分支;緊半代數集;柱代數分解;胞腔相鄰
1 引言
在固定維數歐幾里得空間中幾何對象的排列是計算幾何和計算機修復幾何設計中的基本對象[1].通常假定在這樣一個排列中每個對象有個簡單的描述,例如,它們是由固定次數的一些多項式所定義的半代數集.在三維空間中,二次曲面所形成的排列是特別重要的,因為它們被廣泛的應用于CAD/CAM,計算機圖表,機器人學[2]以及計算物理學[3-4]等相當多的學科中.因此,在R3中,計算和刻畫緊半代數集所形成排列的連通分支是很必要的.
在計算半代數集所形成排列拓撲性質的許多算法中包含一個基本的組成部分,即柱代數分解算法[5],柱代數分解算法能把一個給定的半代數集分解成一些拓撲胞腔.從而可以計算一個半代數集的三角剖分[6],從這個三角剖分可以計算半代數集的連通分支,同調群等.但做柱代數分解時有一個缺點,即要使用迭代投影(即在柱代數分解的過程中每一步維數要減少1),并且多項式的數目在每一步過程中都會平方一次.因此,柱代數分解算法的復雜度是雙指數的,這樣在大多數情況下使得計算排列拓撲信息是不實際的.然而,對于低維的一些重要問題使用柱代數分解算法還是很有效的.
從柱代數分解算法中,能夠獲得胞腔相鄰[7-8]的重要信息.非正式地講,在Rn(n≥1)中,兩個不相交的胞腔如果相互接觸,則這兩個胞腔是相鄰的;正式的講,如果兩個胞腔的并是連通的,則這兩個胞腔是相鄰的.相鄰信息是關于柱代數分解一些應用中的必要組成部分.例如,對于n=2和n=3,一個柱形分解構造算法已經被改進,可以使用相鄰信息去規避原始算法[9]的某些時間耗散的步驟.Schwartz和Sharir應用胞腔相鄰去研究運動問題[10],同樣地, Arnon和McCallum在其算法中去求一條實代數曲線的拓撲類型[11].
本文中,應用柱代數分解算法和簡化的胞腔相鄰算法,得到一個刻畫中由n個緊半代數集所組成排列中連通分支的算法.這個算法沒有使用三角剖分.代替地,計算局部柱代數分解.在算法第2步,僅僅計算了部分胞腔相鄰信息,并沒有使用所有的胞腔相鄰信息.本文的胞腔相鄰算法比文獻[7-8]中在平面和中求胞腔相鄰的算法有所簡化.并且為了刻畫連通分支,本文中這些胞腔相鄰算法的輸入是(i=2,3)中的兩個柱形區域或一個柱代數分解,而且在平面中沒有退化的0-胞腔(參看文獻[8]中定義).更多的,本文中胞腔相鄰算法的過程比在文獻[7-8]中算法的過程有所改進.
本文其它部分內容如下,第1節論述關于柱代數分解算法的預備知識.第2節論述平面和中的簡化胞腔相鄰算法.第3節提出一個在中刻畫n個緊半代數集所組成排列中連通分支的算法.第4節對本文進行總結并對將來的工作提出一些想法.
2 柱代數分解算法的預備知識
本小節中,先介紹柱代數分解算法.對于柱代數分解更詳細的內容請看文獻[5-6,12-13].
輸入有限多項式集
輸出的F-符號不變柱代數分解及其代表系.
(1)如果n=1,求出多項式集F的各個多項式的所有實根r1 求出∏(F)在Γ′上的實根函數 (3)由此得到F-符號不變柱代數分解和它的代表系: 定義 2.1給定上的一個多項式有限集合?,中的一個子集S稱為?-不變的,如果?中每個多項式P在S上是不變號的.如果關于的一個柱代數分解中的每個胞腔都是?-不變的,那么這個柱代數分解稱為適應于?. 下面做對適應于單位球面的柱代數分解. 從柱代數分解算法中需要獲得關于胞腔相鄰[7-8]的重要信息.換言之,對某個柱代數分解中的兩個胞腔,需要知道一個胞腔的閉包是否與另一個相交.例如,以上例子中,點(1,0,0)所對應的胞腔相鄰于胞腔 在第2節中將要給出關于胞腔相鄰更多的細節. 圖1 適應于單位球面的柱代數分解 3.1 預備知識 對于適應于多項式所組成一個有限集合?的一個柱代數分解,為了描述獲得所需胞腔相鄰信息的方法,需要下面的內容. 更多地,可以直觀地對胞腔進行如下標記. 對于R上的一個胞腔標記為Ci,當這個胞腔在一維數軸上從左到右數時為第i個胞腔. 更多地,定義關于柱代數分解中的i-胞腔,(0≤i≤3)是指i-維胞腔.在一個柱代數分解中一個l-胞腔和一個k-胞腔的相鄰定義為{l,k}-相鄰. C2代表點 ?1, C3代表集合 {x|?1 C2,1與C2,2為inter-stack胞腔相鄰,C2,2與C3,2為intra-stack胞腔相鄰;C2,2,2與C3,2,2為{0,1}-相鄰. 在本文中,僅考慮緊半代數集Si,等價地, deg(Pi,j(x,y,z))=2,并且,?∈{≤,=}.下面的內容將要給出,在和中,適合于這種情況的柱代數分解中胞腔相鄰算法.由于在文獻[7-8]中主要算法結果的正確性,不難推出本文中關于胞腔相鄰算法的正確性是顯然的.具體詳情請看文獻[7-8]. 在每一個柱形區域中,通過從下向上標記胞腔可以得到這個柱形區域中所有的 intrastack相鄰信息.例如,胞腔Ci,j相鄰于胞腔Ci,j+1.因此,為了得到關于的一個柱代數分解中的胞腔相鄰信息,主要是確定inter-stack相鄰信息.在R2中,通過利用{0,1}-inter-stack相鄰信息和intra-stack相鄰信息,就能確定關于R2的一個柱代數分解中所有其它胞腔相鄰的信息.例如,假定Ci,j是一個 2-胞腔,包含在以 1-胞腔 Ci為基礎的柱形區域中,并且下面和上面分別被兩個 1-胞腔 Ci,j?1和 Ci,j+1所界定,其中 Ci,j?1和 Ci,j+1分別相鄰于 0-胞腔 Ci?1,k1和 0-胞腔 Ci?1,k2(k1≤k2),并且這兩個0-胞腔包含在以 0-胞腔 Ci?1為基礎的柱形區域中,那么,Ci,j相鄰于這個柱形區域中介于胞腔Ci?1,k1和胞腔Ci?1,k2之間所有的胞腔,并且在這個柱形區域中僅僅與這些胞腔相鄰.因此,只要得到中的{0,1}-inter-stack相鄰信息,就能獲得所有的inter-stack相鄰信息.下面的算法給出了關于的一個柱代數分解中{0,1}-inter-stack相鄰信息的描述. 算法 1 輸入關于的一個柱代數分解中分別以0-胞腔c0=(α,0)和1-胞腔 為基礎的2個柱形區域A和B,其中c0相鄰于c1. 輸出L1是柱形區域A和B之間所有{0,1}-inter-stack相鄰信息的表. 1.令L1←?.求柱形區域A中的0-胞腔 得到 2.如果有一個 sj,0≤j≤m,使得 y=yj與柱形區域 B中的某個 1-胞腔相交,令u←直到y=yj與以{(x,y)|α 3.令柱形區域A中的±∞-截面分別相鄰于柱形區域B中的±∞-截面.在柱形區域B中從下向上求1-胞腔,···,(l≥0).對j=1,···,m做以下3步: 3.1.令n←0和nj←是x=u與柱形區域B中介于y=yj?1和y=yj之間1-胞腔的相交數目. 3.2.在L1中,柱形區域A中的0-胞腔相鄰于柱形區域B中的1-胞腔,···. 3.3.令n←n+nj. 如果c0在c1的右邊,重復算法1. 算法 2 輸入關于的一個柱代數分解. 輸出I是這個柱代數分解中所有胞腔的指標表.L是這個柱代數分解中所有胞腔相鄰信息的表. 1.令I←?.令L←?.構造柱代數分解(平面)所誘導的柱代數分解(線)中的胞腔指標Ci,(1≤i≤2n+1,n≥0).對i=1,···,2n+1做以下2步: 2.2.記錄這個柱形區域中intra-stack相鄰信息到L中. 2.對i=1,···,2n,利用算法1,輸入分別以Ci和Ci+1為基礎的2個柱形區域,然后添加輸出L1到L中(注意,由算法1所輸出的胞腔相鄰信息中的胞腔必須首先轉換成關于的柱代數分解中所對應的胞腔指標). 3.正如第2.2節中第2段所述,使用目前L中的信息可以推出關于的這個柱代數分解中其它inter-stack相鄰信息,然后添加到L中. 算法 3 輸入關于的一個柱代數分解中的2個柱形區域A和B,并且A和B分別是以中的一個0-胞腔c0=(α,β),α,β∈R和一個1-胞腔c1為基礎的柱形區域,其中c0相鄰于c1. p=(ρ,σ),(ρ,σ∈是c1中的一個樣本點.F(x,y,z)∈[x,y,z]使得H(z)=F(α,β,z)的根定義柱形區域A,F(ρ,σ,z)的根定義柱形區域B.G(x,y)∈(x,y)關于x或y或兩個的次數是正的.c1和c0包含在Zero(G(x,y))(即G(x,y)實根的集合)中. 輸出L是柱形區域A和B之間所有的{0,1}-inter-stack相鄰信息表. 1.如果 degy(G)>0,然后令 P(x,z)← Resy(G,F)(F和 G關于 y的結式),否則如果degx(G)>0,然后令P(y,z)←Resx(G,F)(F和G關于x的結式).不失一般性,從現在開始假定G關于y的次數是正的,并且c1在c0的右邊,因此在這步計算P(x,z). 2.令 J=Proj({P(x,z)}).求 J中元素的實根,得到 b∈使得 P定義 2個分別以 (α,0)和 {(x,z)|α 3.1.縮小關于這個根的孤立區間直到這個區間只與P(?b,z)的一個根的唯一孤立區間相交,獲得s1唯一的投影1-胞腔t1; 3.2.令 t0是柱形區域 A′中 t1唯一的邊界 0-胞腔 (從 L1中獲得),然后縮小關于P(α,z)和H(z)的根的孤立區間直到對應于t0的關于P(α,z)的根的孤立區間與H(z)的一個根的唯一孤立區間相交,即求出了柱形區域A中s1的邊界0-胞腔. 算法 4 輸入關于的一個柱代數分解中的2個柱形區域A和B,并且A和B分別是以中的一個1-胞腔c1和一個2-胞腔c2為基礎的柱形區域,其中c1相鄰于c2. 輸出L是柱形區域A和B之間所有的{1,2}-inter-stack相鄰信息表. 1.如果關于R的誘導柱代數分解中存在一個1-胞腔 使得c1和c2包含在以c′為基礎的柱形區域中,并且c2在c1的上面(下面).令是c′中的樣本點,計算 得到關于R2的一個柱代數分解中的2個柱形區域A′和B′,并且這2個柱形區域分別以0-胞腔和1-胞腔 為基礎.利用算法1,輸入A′和B′,得到輸出L′,然后添加L′到L. 否則2.如果關于R的誘導柱代數分解中存在一個0-胞腔c0=(α1,0),(α1∈)使得c1包含在以c0為基礎的柱形區域中,并且c2在c1的右面(左面).令(α1,β),(β∈)是c1中的樣本點,計算{(x,y)|α1 如果c0和c2是關于的一個柱代數分解中的一個0-胞腔和一個2-胞腔,并且c0相鄰于c2,那么恰好在關于的這個柱代數分解中存在2個1-胞腔使得同時相鄰于c0和c2. 算法 5 輸入關于的一個柱代數分解中的2個柱形區域A和B,并且A和B分別是以中的一個0-胞腔c0=(α,β),α,β∈和一個2-胞腔c2為基礎的柱形區域,其中c0相鄰于c2. 輸出L是柱形區域A和B之間所有的{0,2}-inter-stack相鄰信息表. 1.選擇一個1-胞腔c1,使得c1同時相鄰于c0和c2. 2.對柱形區域B中的每個2-胞腔s2,利用算法4,從以c1為基礎的柱形區域中得到s2的邊界1-胞腔t1. 3.利用算法3,從柱形區域A中得到t1的邊界0-胞腔t0.那么對于t1而言,{t0,s2}是柱形區域A和B之間唯一的{0,2}-inter-stack相鄰,添加它到L中. 算法 6 輸入關于的一個柱代數分解. 輸出I是這個柱代數分解中所有胞腔的指標表.L是這個柱代數分解中所有胞腔相鄰信息的表. 1.令 I←?.令 L←?.利用算法 2,輸入關于這個柱代數分解 ()誘導的柱代數分解(平面上),獲得關于誘導柱代數分解(平面上)的輸出I′和L′.對每個胞腔Ci,j做以下2步: 1.2.記錄這個柱形區域中的intra-stack相鄰信息到L中. 2.對L′中的每對相鄰胞腔{c,d},根據c和d的維數,選擇以下3種情況中的一種,在這個柱代數分解(R3)中求以這2個相鄰胞腔為基礎的柱形區域之間的某些inter-stack相鄰信息. 2.1.令 c0=(α,β),α,β∈和 c1是一對相鄰胞腔.令關于的這個柱代數分解中以 c0和 c1為基礎的 2個柱形區域分別是 A和 B.令 p=(ρ,σ),ρ,σ∈是 c1中的樣本點,H(z)=F(α,β,z)的根定義柱形區域A,F(ρ,σ,z)的根定義柱形區域B.令c0和c1包含在Zero(G(x,y))中.利用算法3,輸入c0,c1,A,B,p,H(z),F(α,β,z)和G(x,y),得到輸出L?.注意,在修改L?中元素的指標后,添加它們到L中. 2.2.令c1和c2是一對相鄰胞腔.令關于的這個柱代數分解中以c1和c2為基礎的2個柱形區域分別是A和B.利用算法4,輸入A,B,c1和c2,得到輸出L?.注意,在修改L?中元素的指標后,添加它們到L中. 2.3.令c0和c2是一對相鄰胞腔.令關于的這個柱代數分解中以c0和c2為基礎的2個柱形區域分別是A和B.利用算法5,輸入A,B,c0和c2,得到輸出L?.添加L?中的元素到L中. 3.使用L中現有的內容推出關于這個柱代數分解其它的inter-stack相鄰信息.添加它們到L中. 這些胞腔包含在S中,并且在這個柱代數分解中只有這些胞腔包含在S中.更多地,C2,2,2相鄰于,,和;相鄰于,和;相鄰于, C3,3,4和C4,2,2;C4,2,2相鄰于C3,3,2和C3,3,4.所以S是半代數連通的,即在S中僅有一個連通分支.這個連通分支能被刻畫為: 下面給出刻畫連通分支的算法. 算法 7 輸入中 n個緊半代數集的并集 S,其中每個集合 Si,(1≤i≤n)由有限個集合的并集所定義,其中 輸出S中連通分支的刻畫D. 1.對每個 做以下4步: 1.1.計算適應于集合{Si,1,···,Si,ki}的一個柱代數分解. 1.2.利用算法6,輸入這個柱代數分解,得關于此柱代數分解中所有胞腔相鄰信息的表. 1.3.確定這個柱代數分解中所有包含于Si的胞腔. 1.4.刻畫Si中所有的連通分支{,,···,}. 2.對{S11,1,S11,2,···,}和{,,···,},做以下幾步: 2.1.令 2.1.1.搜索 {S1,α1,···,S1,αw}? {S1,p1{,···,S1,pe},滿足 S1,α1∩[ξ,η]×??,···, S1,αw∩[ξ,η]×??.{S2,β1,···,S2,βv}?S2,q1,···,S2,qf},滿足 2.1.2.求適應于集合{S1,α1,···,S1,αw,S2,β1,···,S2,βv}的一個柱代數分解. 2.1.3.利用算法6,輸入這個柱代數分解,得關于這個柱代數分解中所有包含于[ξ,η]×的胞腔相鄰信息的表. 2.2.由第 2.1步中的內容,得到 S1∪S2中所有連通分支 {,,···,}的刻畫.令S1←S1∪S2. 3.對{S12,1,S12,2,···,}和{S31,1,S31,2,···,},重復第 2步,得到 S1∪S3中所有連通分支{,,···,}的刻畫.令S1←S1∪S3. 4.重復第3步,得到S1∪Sr,(3≤r≤n)中所有連通分支{,,···,}的刻畫.添加S=S1∪Sn中所有連通分支{,,···,}的刻畫到D中. 算法 7的正確性由柱代數分解算法和前面胞腔相鄰算法的正確性所保證.注意,在算法7中的每1步,通過計算適應于在R[x1,x2,x3]中一個有限多項式集的柱代數分解和使用算法6,能確定所有包含于上面這些多項式所定義集合中胞腔相鄰的信息.使用這些胞腔相鄰信息,多項式所定義集合能作為有限數目半代數連通分支不相交的并,而且這些連通分支能被刻畫.通過迭代,能獲得排列中所有的連通分支.而且算法7能在有限步內結束.更多地,對空間中給定的一個點,能夠判斷這個點是否包含于某個連通分支.這個方法能被應用于碰撞檢測,機器人學等領域. 參考文獻 [1]Halperin D,Sharir M.Arrangements and Their Applications in Robotics:Recent Developments.In WAFR: Proceedings of the Workshop on Algorithmic Foundations of Robotics[M].Natick:Springer-Star,1995. [2]Rimon E,Boyd S.Obstacle collision detection using best ellipsoid f i t[J].Journal of Intelligent and Robotic Systems,1997(2):105-126. [3]Lin X,Ng T T.Contact detection algorithms for three-dimensional ellipsoids in discrete element method[J]. International Journal for Numerical and Analytical Methods in Geomechanics,1995,19(9):653-659. [4]Perram J W,Rasmussen J,Praestgaard E,et al.Ellipsoid contact potential:Theory and relation to overlap potentials[J].Physical Review E,1996(6):6565-6572. [5]Collins G E.Quantif i er elimination for real closed f i elds by cylindrical algebraic decomposition[J].Automata theory and formal languages,1975,33(6):134-183. [6]Basu S,Pollack R,Roy M F.Algorithms in Real Algebraic Geometry[M].Berlin:Springer-Verlag,2003. [7]Arnon D S,Collins G E,McCallum S.Cylindrical algebraic decomposition,II:An adjacency algorithm for the plane[J].SIAM J.Comput.,1984,13(4):878-889. [8]Arnon D S,Collins G E,McCallum S.An adjacency algorithm for cylindrical algebraic decompositions of three-dimensional space[J].J.Symbolic Comput.,1988(5):163-187. [9]Arnon D S.Algorithms for the Geometry of Semi-Algebraic Sets[M].Madison:Springer-Vienna,1981. [10]Schwartz J,Sharir M.On the piano movers′problem II.General techniques for computing topological properties of real algebraic manifolds[J].Advances in Applied Mathematics,1983(4):298-351. [11]Arnon D S,McCallum S.A polynomial-time algorithm for the topological type of a real algebraic curveextended abstract[J].Rocky Mountain J.Math.,1984(4):849-852. [12]Arnon D S,Collins G E,McCallum S.Cylindrical algebraic decomposition,I:The basic algorithm[J].SIAM J.Comput.,1984,13(4):865-877. [13]Chen Yufu.Lectures on Computer Algebra[M].Beijing:Higher education Press,2009. Description of the connected components of arrangements Gao Ben We give an algorithm for computing connected components of arrangements of n compact semialgebraic sets inby using the methods of cylindrical algebraic decomposition and simplif i ed cell adjacencies. connected component,compact semi-algebraic set,cylindrical algebraic decomposition, cell adjacency O187.1 A 1008-5513(2014)02-0154-12 10.3969/j.issn.1008-5513.2014.02.006 2013-01-21. 山西省回國留學人員科研資助項目(2013-045);太原理工大學校青年項目基金(2013Z026). 高犇(1985-),博士,講師,研究方向:計算機代數. 2010 MSC:08B8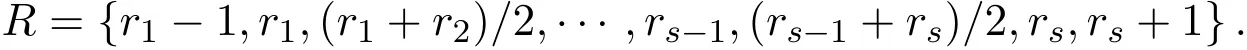
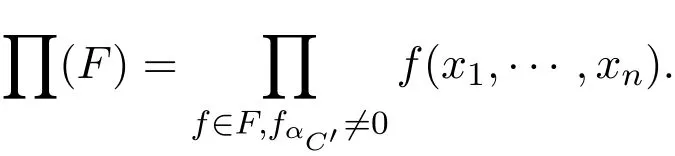
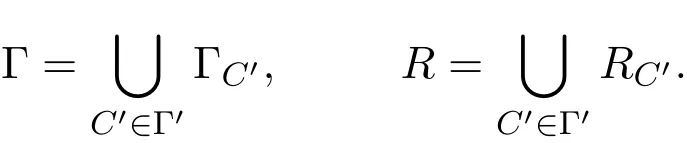
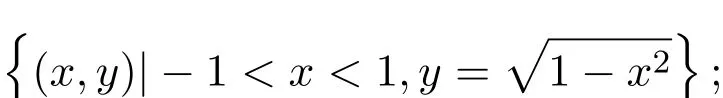
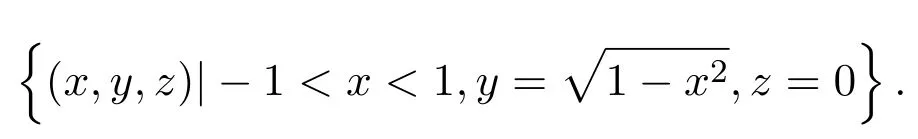
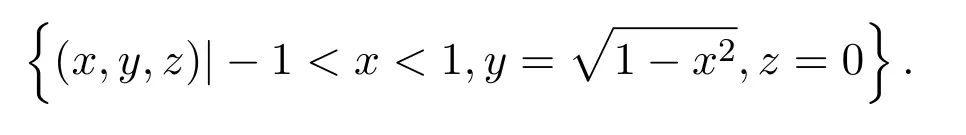
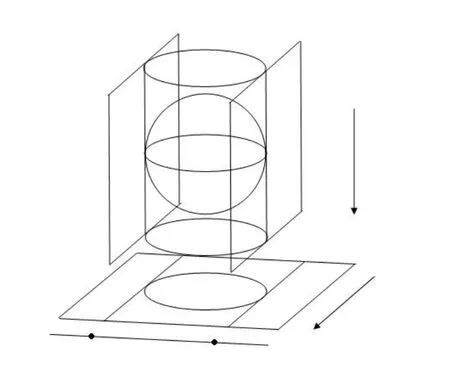
3 胞腔相鄰
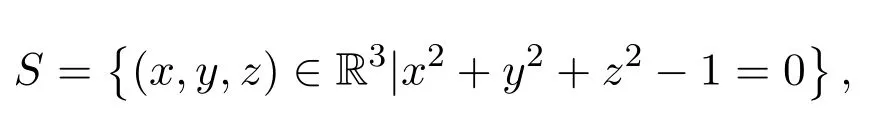
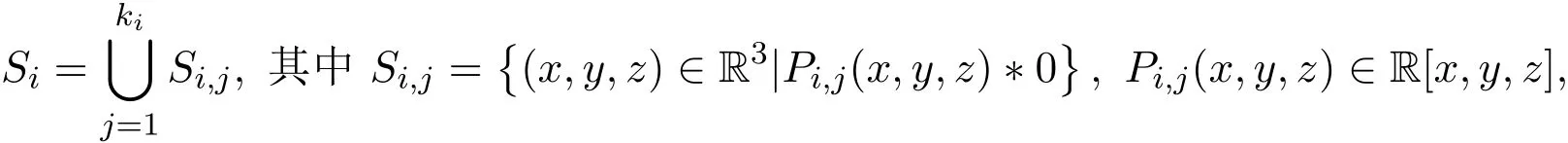
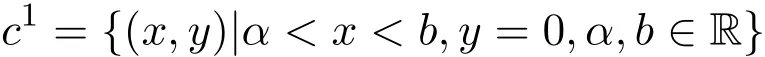
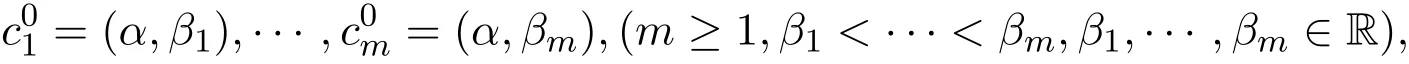
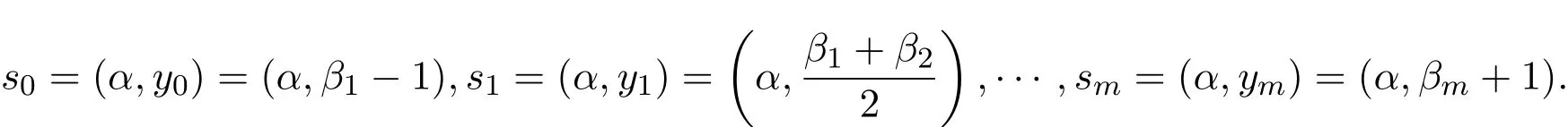
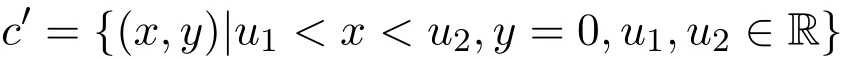
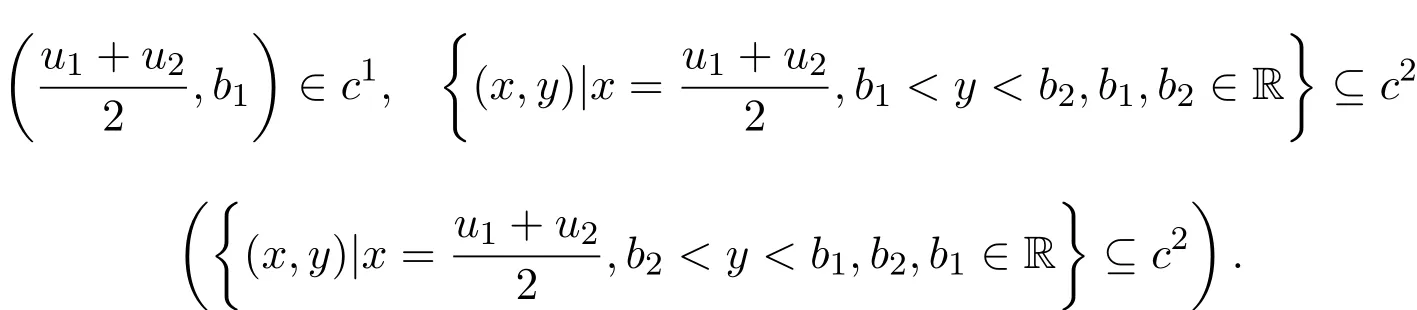
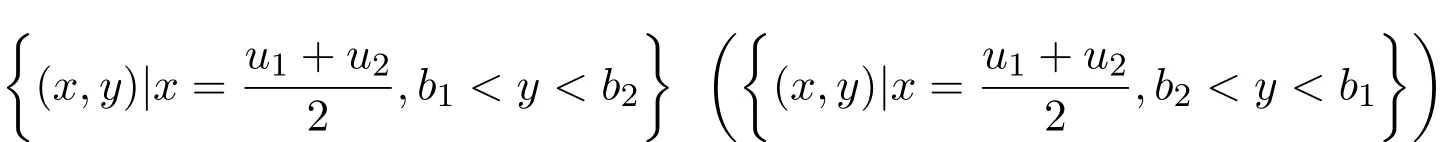
3 刻畫連通分支
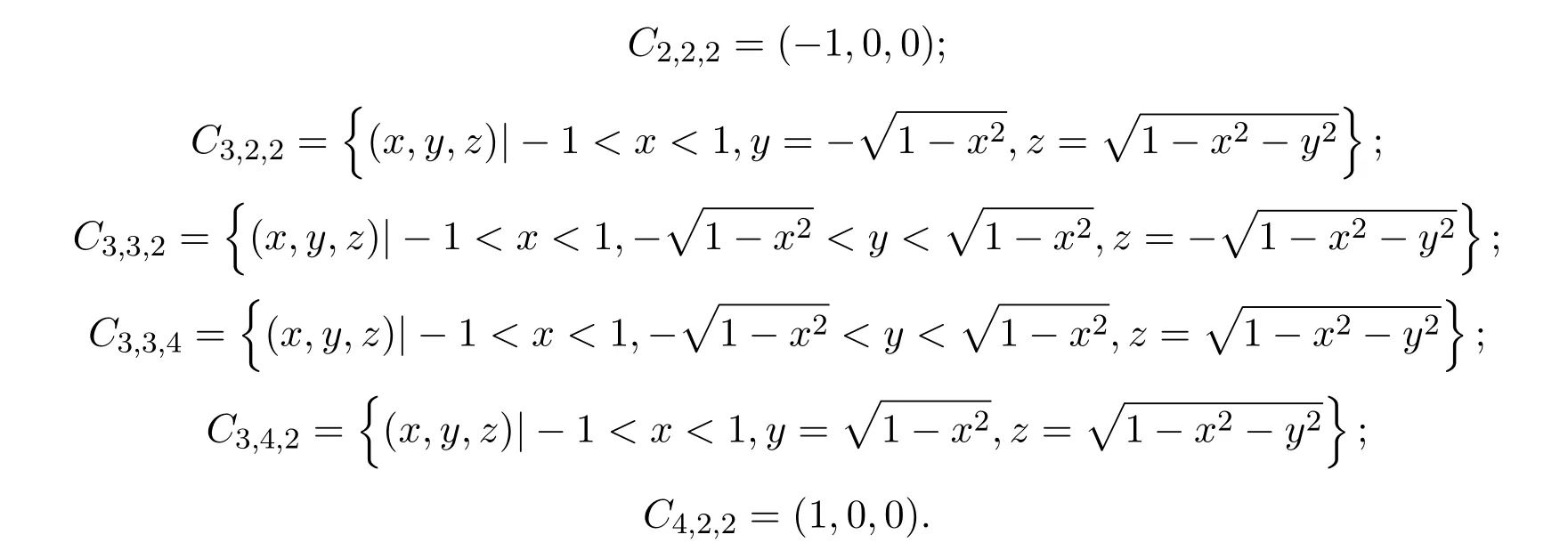
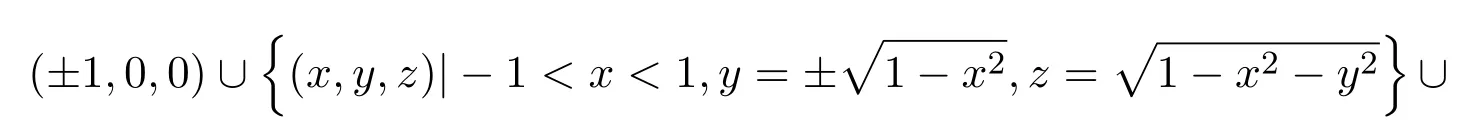
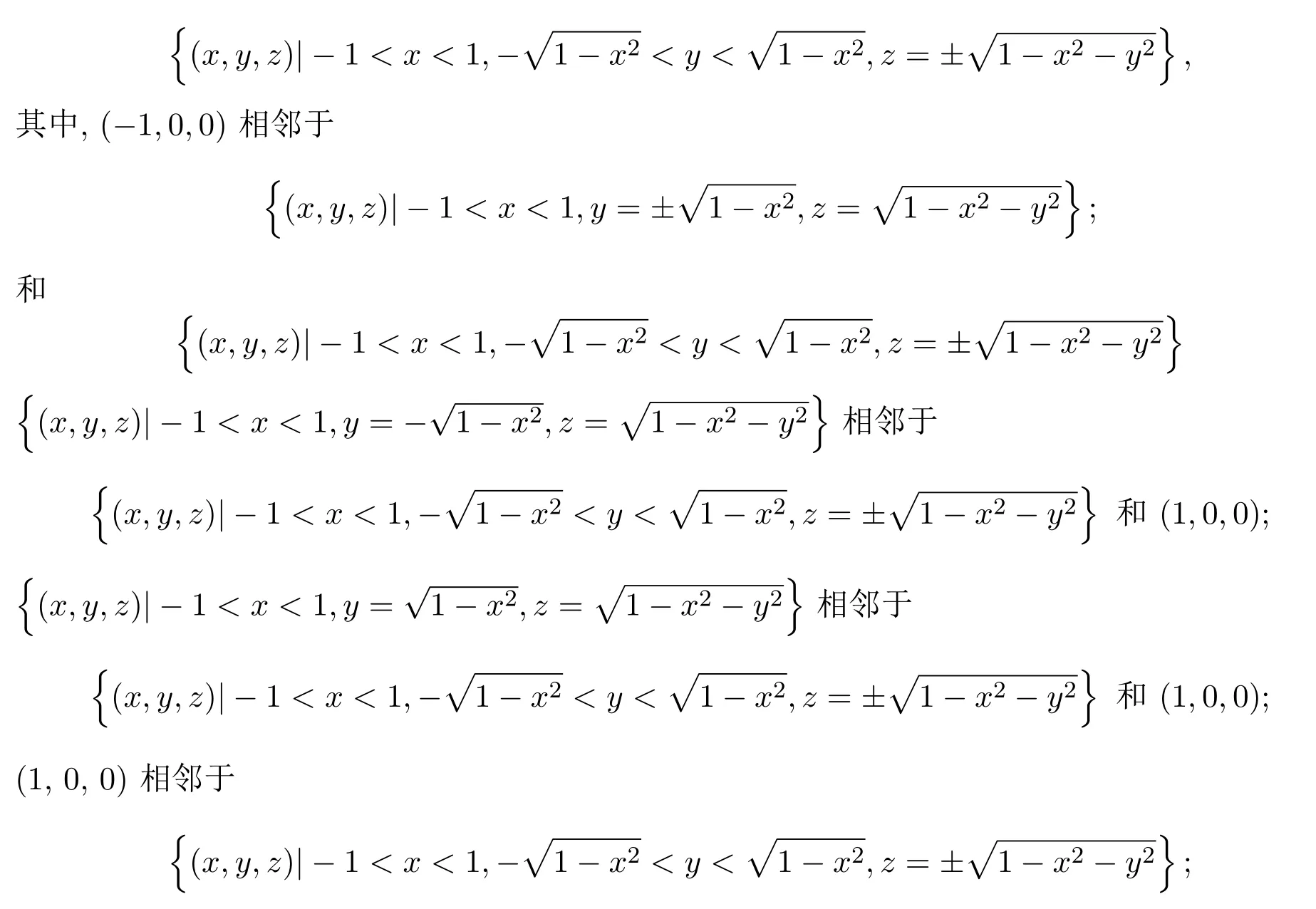
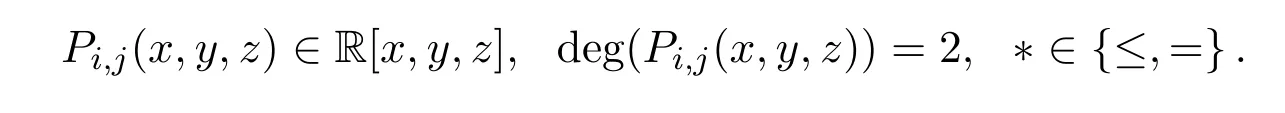
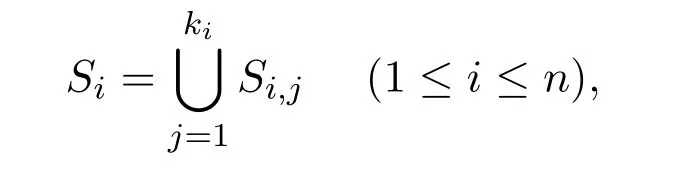
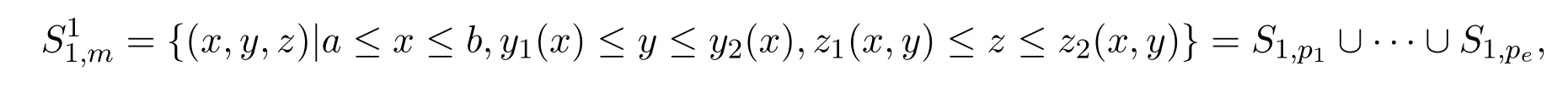
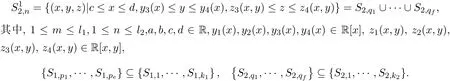

4 結論
(College of Mathematics,Taiyuan University of Technology,Taiyuan 030024,China)

