改進的單純形法迭代計算方法

吳慶豐

淮北師范大學數學科學學院，安徽淮北 235000

改進的單純形法迭代計算方法

吳慶豐

淮北師范大學數學科學學院，安徽淮北 235000

1 引言

單純形法是求解線性規劃的基本方法，許多文獻對其不斷改進。若求解線性規劃問題時，存在基可行解或對偶問題的基可行解，則可直接采用文獻[1]的方法。文獻[2]給出了一種新的原對偶單純形法，文獻[3-4]提出了一種push-to-pull的單純形算法，文獻[5]提出了一種求解線性規劃的新單純形類算法，并與H.Arsham提出的push-to-pull算法作了比較，文獻[6]提出了一種修正的二分單純形法，文獻[7-8]給出了求解線性規劃的攝動單純形法，文獻[9]提出了基于矩陣初等變換初始可行基的獲得方法，得到基于單純形法的求解線性規劃模型的直接方法。文獻[9]的方法其實是對初始系數矩陣進行初等行變換得到一個單位子矩陣，給出了一種新的得到初始可行基的思路，但此法主要是在進行人工計算時可一定程度簡化計算，不便于將算法在計算機上實現，而且在計算機上編程實現該算法也很難降低計算量。如果算法能與計算機結合起來，便于在計算機上實現，那么將更利于實際應用，特別是較大規模的線性規劃問題求解更需要借助于計算機。本文給出的算法既考慮到利用人工計算求解線性規劃能夠簡化計算降低計算量，更重要的是又考慮算法與計算機相結合。

設有線性規劃問題：

其中c∈Rn，x∈Rn，A∈Rm×n，b∈Rm，b≥0，這里向量均為列向量。將系數矩陣A按列分塊，A=(p1，p2，…，pn)，設B是可行基，cB為基B對應的目標系數，檢驗數σj=cj-cTBB-1pj，j=1，2，…，n。

單純形法的基本思想是從一個基可行解向相鄰的另一個改進的基可行解迭代，當所有檢驗數σj≤0時，線性規劃問題達到最優解。

單純形法計算中的幾個問題：

（1）目標函數極小化時解的最優性判別。這時只需以所有檢驗數σj≥0作為判別表中解是否最優的標志。

（2）退化。按最小比值來確定換出基的變量時，有時出現存在兩個以上相同的最小比值，從而使下一個表的基可行解中出現一個或多個基變量等于零的退化解。退化解的出現原因是模型中存在多余的約束，使多個基可行解對應同一頂點。當存在退化解時，就有可能出現迭代計算的循環，盡管可能性極其微小。為避免出現計算的循環，1974年勃蘭特（Bland）提出了一個簡便有效的規則：（1）當存在多個σj＞0時，始終選取下標值為最小的變量作為換入變量；（2）當計算θ值出現兩個以上相同的最小比值時，始終選取下標值為最小的變量作為換出變量。

（3）無可行解的判別。當線性規劃問題中添加人工變量后，無論用人工變量法或兩階段法，當求解結果出現所有σj≤0時，如基變量中仍含有非零的人工變量（兩階段法求解時第一階段目標函數值不等于零），表明問題無可行解。

2 大M法

若化為標準形后的線性規劃問題中約束條件的系數矩陣中不存在單位矩陣，引入人工變量。下面通過舉例說明大M法求解線性規劃以便于與改進的大M法進行比較。

例1用單純形法求解線性規劃問題

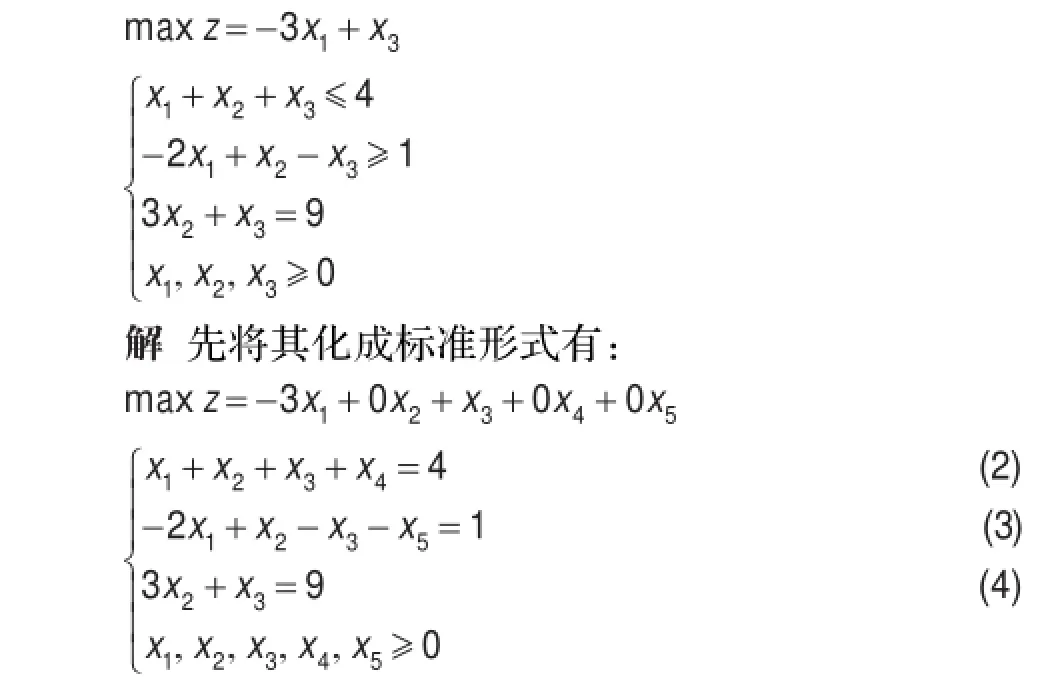
這種情況下，可以通過添加兩列單位向量p6，p7，使連同約束條件中的向量p4構成單位矩陣：

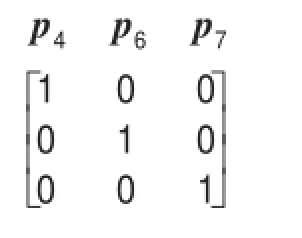
p6，p7是人為添加上去的，它相當于在上述問題的約束條件式（3）中添加變量x6，約束條件式（4）中添加變量x7，變量x6，x7相應稱為人工變量。由于約束條件式（3）、式（4）在添加人工變量前已是等式，為使這些等式得到滿足，在最優解中人工變量取值必須為零。為此，令目標函數中人工變量的系數為任意大的負值，用“-M”代表。“-M”稱為“罰因子”，即只要人工變量取值大于零，目標函數就不可能實現最優。因而添加人工變量后，例1的數學模型形式就變成為：

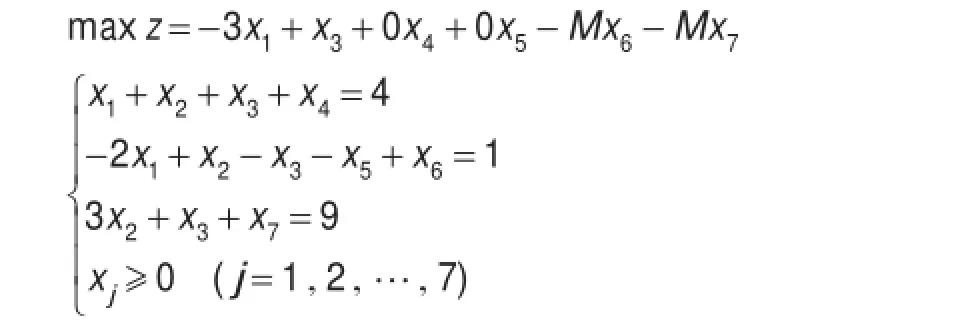
該模型中與p4，p6，p7對應的變量x4，x6，x7為基變量，令非基變量x1，x2，x3，x5等于零，即得到初始基可行解x(0)=(0，0，0，4，0，1，9)T，并列出初始單純形表，在單純形法迭代運算中，M可當作一個數學符號一起參加運算。檢驗數中含M符號的；當M的系數為正時，該檢驗數為正，當M的系數為負時，該項檢驗數為負。例1添加人工變量后，用單純形法求解的過程見表1。

表1 大M法迭代過程

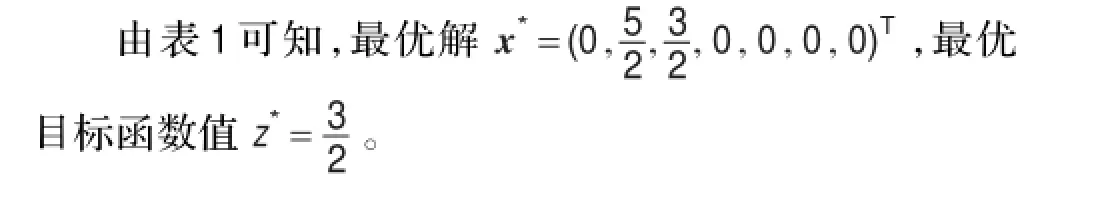
3 改進的大M法

當計算檢驗數表達式中含有M時，結果為（系數×M±常數），因為M很大，很明顯，其值的符號和大小由M的系數符號和大小決定，所以在計算時，只需計算含有M的部分的值即可。這樣可以降低一些運算量。另外，在單純形法迭代過程中，當人工變量全部由基變量變成非基變量時，可以在單純形表中將人工變量部分的表格去掉，然后繼續進行計算，這樣可以再次降低運算量。

為了方便下文敘述，這里將上述方法計算含有M表達式的檢驗數稱為有效檢驗數。有效檢驗數：當計算檢驗數表達式含有M時，只計算含有M的表達式的值；當不含M時，按照原公式計算。

下面給出改進的大M法的計算步驟：

第1步添加人工變量得初始基可行解，列出初始單純形表。

第2步最優性檢驗。

計算有效檢驗數。如表中所有有效檢驗數σj≤0，當基變量中含有非零的人工變量時，則問題無可行解，基變量中不含有人工變量時，表中的基可行解即為最優解（此時，當某非基變量有效檢驗數為零時，問題有無窮多最優解，否則有唯一最優解），計算結束。當表中存在σj＞0時，如有pj≤0，則問題為無界解，計算結束；否則轉下一步。

第3步檢驗是否去掉人工變量。當表中人工變量有效檢驗數σj≤0時，人工變量由基變量變為非基變量，此時去掉含有人工變量部分的表格，轉下一步。

第4步從一個基可行解轉換到相鄰的目標函數值更大的基可行解，列出新的單純形表。

（1）確定換入基的變量。只要有檢驗數σj＞0，對應的變量xj就可作為換入基的變量，當有一個以上檢驗數大于零時，一般從中找出最大一個σk。

σk=max{σj|σj＞0}

其對應的變量xk，作為換入基的變量（簡稱換入變量）。（2）確定換出基的變量。由下式確定θ：

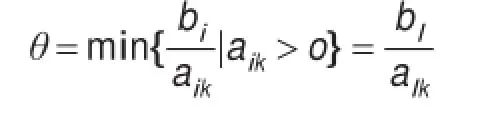
確定xl，是換出基的變量（簡稱換出變量）。元素alk決定了從一個基可行解到相鄰基可行解的轉移去向，取名主元素。

（3）用換入變量xk替換基變量中的換出變量xl，得到一個新的基(p1，…，pl-1，pk，pl+1，…，pm)。對應這個基可以找出一個新的基可行解，并相應地可以畫出一個新的單純形表。

第5步重復第2～4步，一直到計算結束為止。

這里采用改進的大M法求解例1，求解過程見表2。

表2 改進的大M法迭代過程

計算結果同表1，但比較表1和表2的計算過程不難發現，表2在計算檢驗數時，如果結果含有M則不必計算含M的表達式所加減的那些常數，這樣使得計算過程簡化，而且表2迭代計算到第二次時，人工變量已經由基變量變為非基變量，此時基可行解中人工變量取0，此后計算過程直接去掉了人工變量部分的表格，從而再次降低計算量。

4 改進的大M法與兩階段法相結合的算法

實際上，當檢驗數表達式中含有M時，只需計算M的系數即可，從而再次簡化運算，當存在M的系數為正時，只考慮M的正系數部分來確定換入基的變量，取最大的正系數對應的決策變量作為入基變量。出基變量的選擇與原來相同。當然此法更重要的是利用計算機求解時可以克服M的選取與aij，bi或cj的參數值之間的不良影響所導致的計算結果錯誤。下面的方法無需給出M。

設式（1）為標準化的線性規劃問題，添加人工變量得到初始單位基矩陣，將式（1）化為如下線性規劃問題。

這里x=(x1，…，xn，xn+1，…，xn+m)T，e=(1，1，…，1)T∈Rm。

計算檢驗數時，若表達式含有某些人工變量的目標系數cn+1，cn+2，…，cn+m，記為1，2，…，r，r≤m，顯然1，2，…，r的值均為-1，則檢驗數為：

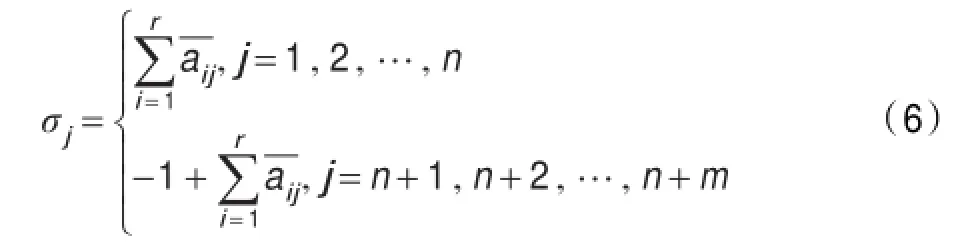
此算法的詳細步驟跟改進的大M類似，只是目標函數不含M，計算檢驗數時有一點差別，這里不再贅述。

5 收斂性分析

單純形方法是求解線性規劃問題的出現較早的一個算法，在理論和實踐上都比較完善，但它不是多項式時間算法。在采用Bland’s法則進行轉軸操作（相同值的情況下取字典序最小）之后，可以證明單純形法一定能夠在有限步之后終止[10-11]，但是最壞情況算法的時間復雜度為指數級別的，而且可以構造出讓單純形法的時間復雜度達到指數級別的具體實例。不過實踐證明在絕大多數情況下單純形法的效率非常令人滿意。單純形法的最壞時間復雜度為指數級別，并不意味著線性規劃不存在多項式級別的算法。橢球算法和內點算法均為解決線性規劃的多項式時間算法。雖然Khachigan和Karmarkar分別在1979年和1984年提出了求解線性規劃問題的多項式時間算法。但就計算工作量而言，一般情況下都沒有單純形方法好。從大量數值計算結果分析，K-變形算法優于Karmarkar算法，從同一內點出發達到同樣精度要求的解所需迭代次數，K-變形方法要優于Karmarkar方法，而對多數問題來說，單純形法又優于K-變形方法和Karmarkar方法，但也有一些情況下單純形法不如Karmarkar方法和K-變形方法。通過大量的計算表明，對于多數問題來說，單純形法要明顯地優于Karmarkar算法及其變形算法[12]。

本文算法主要改進有：

（1）計算檢驗數時，只計算有效部分使得計算簡化。

（2）迭代到適當步驟，去掉人工變量，減小計算規模，降低計算量，減少存貯空間。

（3）解決利用計算機求解時由于大M值的影響所可能導致的錯誤。

本文給出的算法不會減少迭代次數，但會降低計算量及計算機存貯空間，由于不改變迭代次數，從任一基可行解開始，采用Bland’s法則進行轉軸操作一定能夠在有限步之后終止。要減少迭代次數，需要改變樞軸元素選取準則。文獻[13]提出一種新的入基準則為最大加權檢驗數準則，并利用隨機模擬方法將該入基準則與其他入基準則進行比較，結果表明該準則優于最大檢驗數準則和最大上升準則。文獻[14]給出了一種新的選擇入基變量的準則，減少了單純形法的迭代次數。文獻[15]給出了一個新的迭代進出基準則即最大增量準則，可以加快迭代速度，同時也可以避免迭代中可能遇到的所謂循環。但文獻[16]通過大規模的數值實驗結果表明，文獻[15]這種改進的單純形算法雖然在大部分問題上的迭代次數比經典的單純形算法有所減少，但所耗費的計算時間卻普遍增加，其計算效率隨著問題規模的增大而不斷下降。文獻[17]給出了單純形法中確定主元素的兩個新法則，即按使目標函數值增加得最多的原則確定主元素和按使目標函數值增加得最快的原則確定主元素，具有迭代次數更少、收斂速度更快的特點。本文所給出的算法也可以采用如文獻[13-14，17]等所提供的新的樞軸主元的選取方法，迭代次數相應會有所降低。

6 結束語

用大M法處理人工變量，在用手工計算求解時不會碰到麻煩。但用電子計算機求解時，對M就只能在計算機內輸入一個機器最大字長的數字。如果線性規劃問題中的aij，bi或cj等參數值與這個代表M的數相對比較接近，或遠遠小于這個數字，由于計算機計算時取值上的誤差，有可能使計算結果發生錯誤。為了克服這個困難，通常可以對添加人工變量后的線性規劃問題分兩個階段來計算，稱兩階段法。而兩階段法需要將目標函數分為兩個階段，破壞了目標函數的一致性。這里也可以采用本文給出的兩種改進的方法，可以避免由計算機求解時由于M的選取與aij，bi或cj的參數值以及計算機計算誤差所產生的不良影響。并當人工變量全部由基變量變成非基變量時，可以在單純形表中將人工變量部分的表格去掉，這樣相當于又結合了兩階段法的優點。實際上，人工變量的出現只是為了方便得到初始單位基矩陣，在計算過程中，如果到某一步人工變量全部由基變量變成非基變量而此時仍需繼續迭代計算時，由于基可行解中非基變量取0，所以此時完全沒有必要繼續帶著人工變量進行計算。

[1]程理民，吳江，張玉林.運籌學模型與方法教程[M].北京：清華大學出版社，2007.

[2]燕子宗，費浦生，萬仲平.線性規劃的單純形法及其發展[J].計算數學，2007，29（1）：1-14.

[3]Arsham H.An algorithm for simplex tableau reduction：the push-to-pull solution strategy[J].Applied Mathematics and Computation，2003，137（2）：525-547.

[4]Arsham H，Baloh P，Damij T，et al.An algorithm for simplex tableau reduction with numerical comparison[J].International Journal of Pure and Applied Mathematics，2003，4（1）：53-80.

[5]李煒.一個新的單純形類算法[J].數學理論與應用，2003，23（3）：118-122.

[6]Pan P Q.A modified bisection simplex method for linear programming[J].Journal of Computational Mathematics，1996，14（3）：249-255.

[7]Pan Pingqi.A new perturbation simplex algorithm for linear programming[J].Journal of Computational Mathematics，1999，17（3）：233-242.

[8]Pan Pingqi.Primal perturbation simplex algorithms for linear programming[J].Journal of Computational Mathematics，2000，18（6）：587-596.

[9]申卯興，許進.求解線性規劃的單純形法的直接方法[J].計算機工程與應用，2007，43（30）：94-96.

[10]Bland，Robert G.New finite pivoting rules for the simplex method[J].Mathematics of Operations Research，1977，2（2）：103-107.

[11]周勤學，丘兆福.Bland避免循環的單純形方法的改進[J].中山大學學報：自然科學版，1989，28（3）：113-115.

[12]王曉慧，邢麗君.單純形法與Karmarkar算法及其變形算法的比較[J].東北電力學院學報，1997，17（1）：28-33.

[13]林福榮，陳東宜.單純形法的一種新的入基準則[J].曲阜師范大學學報：自然科學版，2002，28（4）：25-28.

[14]申卯興，葉微，劉毅，等.單純形法中樞軸元素選取準則的改進[J].計算機工程與應用，2003，39（25）：57-58.

[15]王全文，吳育華，吳振奎，等.單純形法選擇進出基變元的一個新準則[J].數學的實踐與認識，2009，39（14）：75-81.

[16]高培旺.關于“單純形法選擇進出基變元的一個新準則”的計算效率[J].河南工程學院學報：自然科學版，2012，24（2）：61-64.

[17]羅進，張志軍，劉任河.單純形法中確定主元素的兩個新法則[J].武漢工程大學學報，2008，30（1）：122-124.

WU Qingfeng

School of Mathematical Sciences,Huaibei Normal University,Huaibei,Anhui 235000,China

Improved big-Mmethod is presented.If expressions of the calculated test number containM,the only portion containingMis calculated,and thereby the calculation is simplified.And when artificial variables become nonbasic variables by basic variables in the iterative calculation process,the artificial variables parts of the table can be directly removed and then the calculation is continued.Thus,the amount of computation is again reduced.Taking advantages of two-phase method,an iteration algorithm without giving the bigMis further given.This method does not undermine the consistency of the objective function,and the calculation error can be avoided when using traditional big-Mmethod combined with computer to solve,due to the improper selection of the value ofM.

linear programming;simplex method;big-Mmethod;two-phase method

對傳統大M法進行改進，若計算檢驗數的表達式中含有M則只計算含有M的部分，從而簡化計算，迭代過程中當人工變量由基變量變為非基變量時，直接去掉人工變量部分的表格然后繼續計算，從而再一次降低計算量。借鑒兩階段法的優點進一步給出了無需給出大M的迭代算法，此法不會破壞目標函數的一致性，而且可以避免傳統大M法在利用計算機求解時由于M值的選取不當所導致的計算錯誤。

線性規劃；單純形法；大M法；兩階段法

A

O22

10.3778/j.issn.1002-8331.1210-0107

WU Qingfeng.Improved iterative calculation methods of simplex algorithm.Computer Engineering and Applications, 2014,50（18）：59-62.

安徽省高等學校省級自然科學研究項目（No.KJ2011B152）。

吳慶豐（1979—），男，講師，研究領域：最優化理論及算法。E-mail：wuqingfeng6@163.com

2012-10-12

2013-01-18

1002-8331（2014）18-0059-04

CNKI網絡優先出版：2013-02-07，http://www.cnki.net/kcms/detail/11.2127.TP.20130207.1420.015.html