章魚圖的IC-著色和IC-指數(shù)

楊楊，王力工

（西北工業(yè)大學(xué)理學(xué)院應(yīng)用數(shù)學(xué)系，陜西西安710072）

章魚圖的IC-著色和IC-指數(shù)

楊楊，王力工

（西北工業(yè)大學(xué)理學(xué)院應(yīng)用數(shù)學(xué)系，陜西西安710072）

章魚圖H（Cm，n）是指由圈Cm的一個頂點與星圖STn=K1，n的中心重迭得到的圖，研究了章魚圖H（Cm，n）的IC-著色問題，通過分類討論的方法，分別得到了當(dāng)m=3，4，5，n≥1時章魚圖H（Cm，n）的極大IC-著色和它們相應(yīng)的IC-指數(shù)，并提出章魚圖H（Cm，n）一個上界猜想。

IC-著色；IC-指數(shù)；章魚圖

本文所指的圖均為無向簡單圖，文中未說明的符號和術(shù)語可參考文獻［1］。

設(shè)圖G=(V,E)是一個連通圖，對于圖G的一個著色f:V(G)→?和G的一個子圖H，定義f(H)=∑v∈V(H)f(v)，特別的將f(G)記作S(f)。如果對于任意整數(shù)k∈{1,2,3,…,f(G)}?[1,f(G)]存在G的一個連通子圖H，使得f(H)=k,則稱f為圖G的一個IC-著色。并定義M(G)=max{f(G) f為圖G的一個IC-著色}為圖G的IC-指數(shù)，并且稱適合f(G)=M(G)的IC-著色f為圖G的一個極大IC-著色。

圖的IC-著色問題來源自數(shù)論中郵票問題［2-4］，自從提出以來，得到了廣泛的研究：1995年，Penrice在文獻［4］得到結(jié)論：

1）M(Kn)=2n。

2）當(dāng)n≥2時，M(K1,n)=2n+n。

3）當(dāng)3≤n≤9，n≠7時，M(Cn)=n(n-1)+1。

2005年，Salehi等人在文獻［5］正式提出IC-著色和IC-指數(shù)的概念，并得到結(jié)論：當(dāng)n≥2時，M(K2,n)=3?2n+1。2006年，徐寶根在文獻［6］得到結(jié)論：設(shè)整數(shù)n≥2且b1≥b2≥…≥bn≥2則M(ST(n;b1,b2,…,bn))≥2b1+∑ni=-11(bi+1-1)bin，2008年，Shiue和Fu在文獻［7］得到結(jié)論：當(dāng)2≤m≤n時，M(Km,n)=3?2m+n-2-2m-2+2。2011年，陳劍峰在文獻［8］與［9］當(dāng)中分別得到了笛卡爾積圖Pm×Pn和星的細分圖的IC-指數(shù)的一個下界。2012年，周娟等在文獻［10］得到結(jié)論當(dāng)n=10,12,14時，M(Cn)=n(n-1)+1。2012年，陳劍峰等在文獻［11］和文獻［12］研究了雙星圖的IC-著色，得到了：對于雙星圖DS(m,n)(2≤m≤n)的IC-著色，設(shè)f是G=DS(m,n)的一個極大IC-著色，則當(dāng)f(v1)=1時，有M(G)=(2m-1+1)(2n-1+1)，而且f是唯一的，并由這個結(jié)論得到了雙星圖的IC-指數(shù)為M(DS(m,n))=(2m-1+1)(2n-1+1)。

章魚圖H（Cm，n）是指由圈Cm的一個頂點與星圖STn=K1，n的中心重疊得到的圖，本文研究了章魚圖H（Cm，n）的IC-著色問題，分別得到了當(dāng)m=3，4，5，n≥1時章魚圖H（Cm，n）的極大IC-著色和它們的IC-指數(shù)，并給出章魚圖H（Cm，n）IC-指數(shù)的一個上界猜想。

對于章魚圖H（Cm，n），如圖1。圈的頂點集設(shè)為V(Cm)={ui|1≤i≤m}，星圖的頂點集設(shè)為V(STn)= {vj|1≤j≤n}，記星圖STn的中心為u1=v。

定理1當(dāng)m=3，n≥1時，章魚圖G=H（Cm，n）的IC-指數(shù)滿足

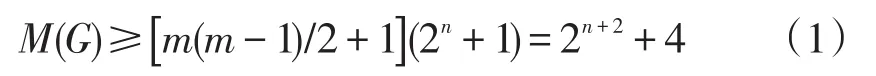
證明當(dāng)m=3,n≥1時，章魚圖G=H(Cm,n)的一個著色記為f，其中f(u1)=5，f(u2)=1，f(u3)=2，f(vj)=2j+1(j=1,2,…,n)，下面證明f是章魚圖G=H(Cm,n)的一個IC-著色。

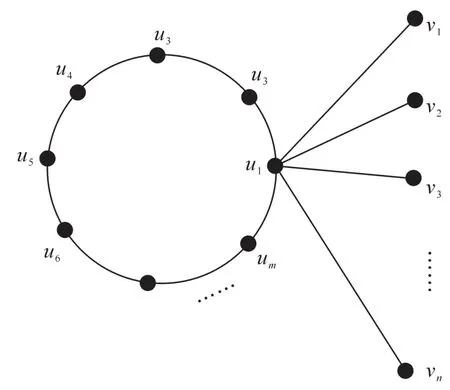
圖1 章魚圖H(Cm,n)Fig.1 Octopus GraphH(Cm,n)

當(dāng)k∈[1,5]時，若k=1，有f(u2)=1；若k=2，有f(u3)=2；若k=3，有f(u2)+f(u3)=3；若k=4，有f(v1)=4；若k=5，有f(u1)=5；當(dāng)k∈[6,2n+1+4]時，記u1=v-1,u2=v0，考慮k-5的展開式：，對k∈[6,2n+2+4]，存在由點導(dǎo)出的連通子圖Hk，使得f(Hk)=k，綜上可知f是章魚圖G=H(Cm,n)的IC-著色，從而得到

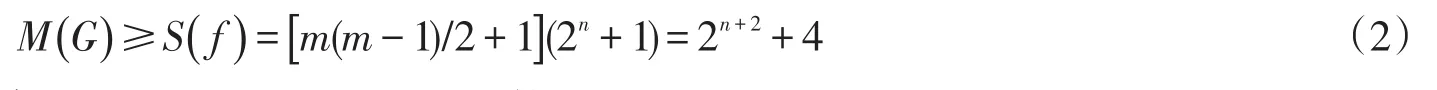
定理2當(dāng)m=3,n≥1時，章魚圖G=H(Cm,n)的IC-指數(shù)為

證明當(dāng)m=3,n≥1時，定理3.1已證得M(G)≥S(f)=[m(m-1)/2+1](2n+1)，下面只需證M(G)≤[m(m-1)/2+1](2n+1)=2n+2+4。設(shè)章魚圖G=H(Cm,n)=H(C3,n)的IC-指數(shù)為M，對k=1,2,3,…，依次尋找圖G的連通子圖Hk，使得f(Hk)=M-k，在著色的過程中，目標是選擇使M最大的方案，下面分步驟進行著色。

步驟1：當(dāng)k=1時，為使連通子圖H1存在，要對章魚圖H(C3,n)上的點著色1，著色為1的點可以為u2或v1。

情況1：當(dāng)f(u2)=1，存在連通子圖H1=G{u2}，使得f(H1)=M-1。

情況2：當(dāng)f(v1)=1，存在連通子圖H1=G{v1}，使得f(H1)=M-1。

步驟2：當(dāng)k=2時，為使連通子圖H2存在，要對章魚圖H(C3,n)上的點著色1或2，在步驟1的情況1下，著色的點可以為u3或v1，在步驟1的情況2下，著色的點可以為u2或v2。為了使得M盡可能大，此步驟中的以下4種情形為最優(yōu)方案。

情況1：當(dāng)f(u2)=1，f(u3)=2，存在連通子圖H2=G{u3}，使得f(H2)=M-2，存在連通子圖H3=G{u2,u3}，使得f(H3)=M-3。

情況2：當(dāng)f(u2)=1，f(v1)=2，存在連通子圖H2=G{v1}，使得f(H2)=M-2，存在連通子圖H3=G{u2,v1}，使得f(H3)=M-3。

情況3：當(dāng)f(u2)=2，f(v1)=1，存在連通子圖H2=G{u2}，使得f(H2)=M-2，存在連通子圖H3=G{u2,v1}，使得f(H3)=M-3。

情況4：當(dāng)f(v1)=1，f(v2)=2，存在連通子圖H2=G{v2}，使得f(H2)=M-2，存在連通子圖H3=G{v1,v2}，使得f(H3)=M-3。

步驟3：顯然在步驟2的4種情形下都存在圖G的連通子圖H3，使得f(H3)=M-3。當(dāng)k=4時，根據(jù)步驟1和步驟2的著色規(guī)則繼續(xù)著色，得到以下7種情況。

情況1：當(dāng)f(u2)=1，f(u3)=2，f(v1)=4，存在連通子圖H4=G{v1}，使得f(H4)=M-4；存在連通子圖H5=G{u2,v1}，使得f(H5)=M-5；存在連通子圖H6=G{u3,v1}，使得f(H6)=M-6；存在連通子圖H7=G{u2,u3,v1}，使得f(H7)=M-7。以下情況同步驟3中的情況1可得，存在連通子圖Hk，使得f(Hk)=M-k，k=4,5,6,7。

情況2：當(dāng)f(u2)=1，f(u3)=4，f(v1)=2。

情況3：當(dāng)f(u2)=1，f(v1)=2，f(v2)=2。

情況4：當(dāng)f(u2)=2，f(u3)=4，f(v1)=1。

情況5：當(dāng)f(u2)=2，f(v1)=1，f(v2)=4。

情況6：當(dāng)f(u2)=4，f(v1)=1，f(v2)=2。

情況7：當(dāng)f(v1)=1，f(v2)=2，f(v3)=4。

繼續(xù)進行著色時，不失一般性，以步驟三的情況1為例，下面依次對點v2,v3,v4,…進行著色。考慮k=8時，為使連通子圖H8存在，需滿足f(v2)+l=8，其中l(wèi)∈{0,1,2,3,4,5,6,7}，易知1≤f(v2)≤8，為保證著色極大，則f(v2)=8，同理可得，為使得f(Hk)=M-k,k=1,2,3,…的連通子圖Hk存在，且保證著色極大，易證除中心v外，余下的點的著色一定為16,32,64,…,2n-1，此時已對章魚圖中的n個點完成著色。

當(dāng)對章魚圖中的n個點（除中心v外）的著色為1,2,4,…,2n-1時，存在一種特殊情形，僅對星圖頂點的著色，著色為f(vj)=2j-1，j=1,2,3,…,n，此時可以找到連通子圖Hk，使得cj=0.1，連通子圖為，從而當(dāng)k=1,2,3,…,2n-1時，可以找到連通子圖Hk，使得f(Hk)=M-k，下面分2種情形繼續(xù)著色。

情形1：當(dāng)f(u1)=1時，H′=G{v,v1,v2,…,vn}=G[u2,u3]為連通子圖且f(H)=M-2n。為使數(shù)M-(2n+1)對應(yīng)一個連通子圖，應(yīng)有f(u2)+l=2n+1，l∈{0,1,2,3,…,2n}，記u2的著色為α，則α≤2n+1，此時M-k都對應(yīng)一個連通子圖，其中k=1,2,3,…,2n+α，再考慮數(shù)M-(2n+α+1)所對應(yīng)的連通子圖，同理有f(u3)≤2n+α+1。當(dāng)f(ui)(i=2,3)都取得最大值時，依次檢驗數(shù)i=1,2,…,2n+2+3，都有連通子圖與之對應(yīng)，此時，極大著色為S(f1)=2n+2+3。

情形2：當(dāng)f(u1)≠1時，為使數(shù)M-2n對應(yīng)一個連通子圖，應(yīng)有f(u2)+l=2n，l∈{0,1,2,3,…,2n-1}，記u2的著色為α，則α≤2n，此時則M-k都對應(yīng)一個連通子圖，其中k=1,2,3,…,2n-1+α，再考慮數(shù)M-(2n+α)所對應(yīng)的連通子圖，同理有f(u3)≤2n+α。當(dāng)f(ui)(i=2,3)都取得最大值時，依次檢驗數(shù)i=1,2,3,…，發(fā)現(xiàn)當(dāng)i=3時，無連通子圖與之對應(yīng)，從而應(yīng)有f(u1)≤3，此時，極大著色為S(f2)=2n+2+2。

當(dāng)對章魚圖中的n個點（除中心v外）的著色為1,2,4,…,2n-1時，除去上述僅對章魚圖中的星圖著色的情況外，繼續(xù)著色，易證，余下點的著色必為2n,2n+1,…；此時，除章魚圖的中心v之外，其它點的著色都已經(jīng)確定。

下面以步驟3中的情況1，情況2的著色為例進行分析。

對于步驟3中的情況1，繼續(xù)著色，著色為f(u2)=1，f(u3)=2，f(vj)=2j+1，j=1,2,…,n，依次檢驗i=1,2,3,…，發(fā)現(xiàn)當(dāng)i=5時，無連通子圖與之對應(yīng)，故對中心v著色使得f(v)+l=5，l∈{0,1,2,4}，易知1≤f(v)≤5，當(dāng)f(v)取得最大值時，依次檢驗i=1,2,3,…,2n+2+4，都有連通子圖與之對應(yīng)，此時，極大著色為S(f3)=2n+2+4。

對于步驟3中的情況2，繼續(xù)著色，著色為f(u2)=1，f(u3)=4，f(v1)=2，f(vj)=2j+1，j=2,3,…,n，依次檢驗i=1,2,3,…，發(fā)現(xiàn)當(dāng)i=3時，無連通子圖與之對應(yīng)，故對中心v著色使得f(v)+l=3，l∈{0,1,2}，易知1≤f(v)≤3，當(dāng)f(v)取得最大值時，依次檢驗i=1,2,3,…,2n+2+2，都有連通子圖與之對應(yīng)，此時，極大著色為S(f4)=2n+2+2。

通過對步驟3的2種著色情況的分析，推廣到所有情況，當(dāng)所有點（除中心v外）的著色確定后，依次檢驗i=1,2,3,…，當(dāng)i=3時，發(fā)現(xiàn)除步驟3的情況1之外，無連通子圖與之對應(yīng)，故對中心v著色使得f(v)+l=3，l∈{0,1,2}，易知1≤f(v)≤3，當(dāng)f(v)取得最大值時，依次檢驗i=1,2,3,…,2n+2+2，都有連通子圖與之對應(yīng)，此時，極大著色為S(f)=2n+2+2。

綜合以上所有情況可知，章魚圖H（Cm，n）=H（C3，n）的著色滿足f(G)≤S(f1)=2n+2+4，結(jié)合定理3.1可知當(dāng)m=3,n≥1時，章魚圖G=H（Cm，n）的IC-指數(shù)為

例1當(dāng)m=3,n≥1時，章魚圖H（Cm，n）=H（C3，n）的極大IC-著色見圖2。

定理3當(dāng)m=4，n≥1時，章魚圖H（Cm，n）的IC-指數(shù)為

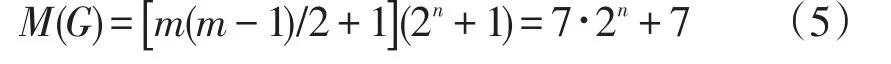
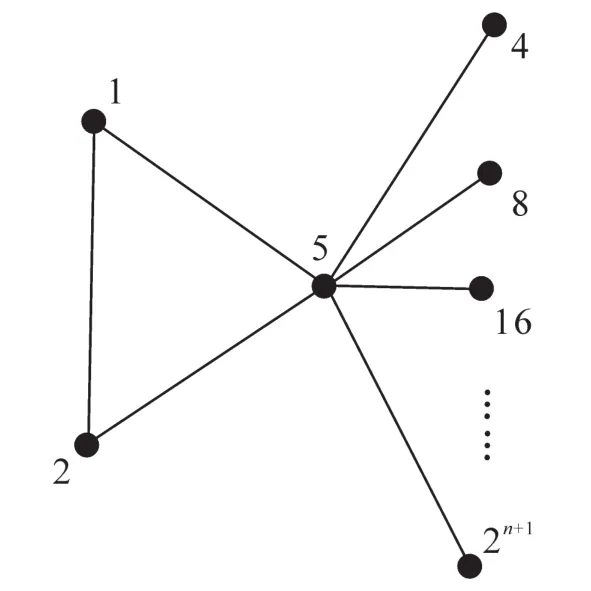
圖2 章魚圖H（C3，n）的極大IC-著色Fig.2 Maximal IC-coloring of H（C3，n）

證明當(dāng)m=4，n≥1時，記章魚圖的著色為f，章魚圖H（Cm，n）=H（C4，n）的著色為f(u1)=8， f(u2)=1，f(u3)=3，f(u4)=2，f(vj)=7?2j-1(j=1,2,…,m)，同定理3.1的證明可得，f是章魚圖G=H（Cm，n）的IC-著色，從而得到當(dāng)m=3,4,n≥1時，M(G)≥S(f)=[m(m-1)/2+1](2n+1)=7?2n+7。

下面證明M(G)≤[m(m-1)/2+1](2n+1)=7?2n+7，設(shè)章魚圖G=H(Cm,n)=H(C4,n)的IC-指數(shù)為M，對k=1,2,3,…，依次尋找連通子圖Hk，使得f(Hk)=M-k，下面分步驟進行著色（由于情況太多，在此不一一列舉），仿照定理3.2的證明，可得當(dāng)m=3,4,n≥1時，M(G)≤S(f)=[m(m-1)/2+1](2n+1)=7?2n+7，從而章魚圖G=H(Cm,n)=H(C4,n)的IC-指數(shù)為M(G)=[m(m-1)/2+1](2n+1)=7?2n+7。

例2當(dāng)m=4,n≥1時，章魚圖H(Cm,n)=H(C4,n)的極大IC-著色見圖3。

定理4當(dāng)m=5,n≥1時，章魚圖G=H(Cm,n)的IC-指數(shù)為

證明當(dāng)m=5,n≥1時，記章魚圖的著色為f，章魚圖G=H(Cm,n)=H(C5,n)的著色為f(u1)=5，f(u2)=1，f(u3)=3，f(u4)=5?2n+5，f(u5)=2，f(vj)=5?2j-1(j=1,2,…,m)，參照定理1和定理2的證明，同理可證得，這一著色是章魚圖G=H(Cm,n)的一種極大IC-著色，IC-指數(shù)為M(G)=11+10×2n。

例3當(dāng)m=5,n≥1時，章魚圖H(Cm,n)=H(C5,n)的極大IC-著色見圖4。

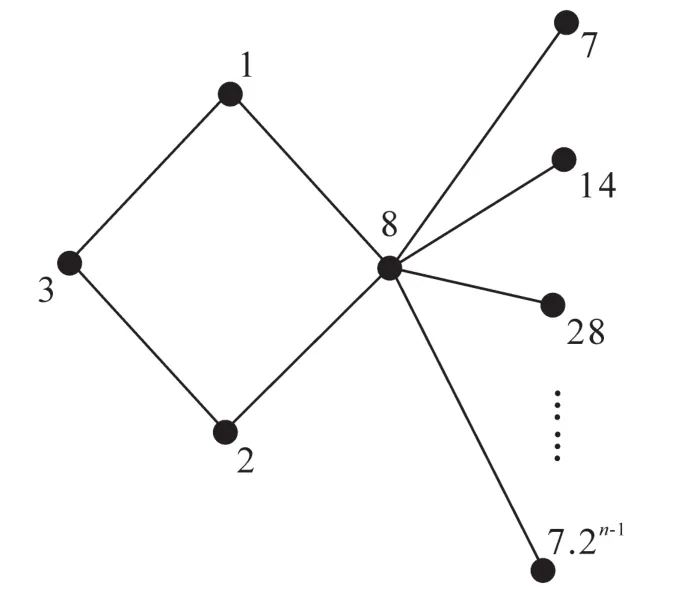
圖3 章魚圖H（C4，n）的極大IC-著色Fig.3 Maximal IC-coloring of H（C4，n）

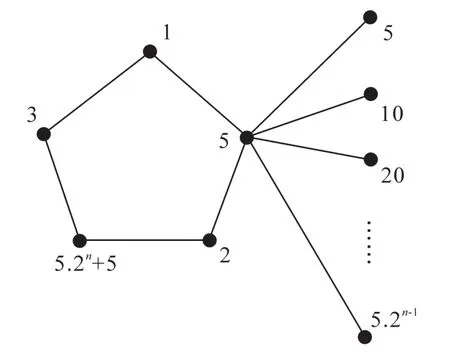
圖4 章魚圖H(C5,n)的極大IC-著色Fig.4 Maximal IC-coloring of Octopus GraphH(C5,n)

猜想當(dāng)m≥3,n≥1時，章魚圖H(Cm,n)的IC-指數(shù)的上界為

[1]SALEHI E,SIN MIN LEE,KHATIRINEJAD M S.IC-colorings and IC-indices of graphs[J].Discrete Mathematics,2005,299(8): 297-310.

[2]ALTER R,BRNETT J A.A postage stamp problem[J].The American Mathematical Monthly,1980,87(3):206-210.

[3]程卓,王殊.基于IC著色的認知差分跳頻系統(tǒng)多址原理[J].武漢大學(xué)學(xué)報:理學(xué)版,2010,56(4):478-482.

[4]PENRICE S G.Some new graph labeling problems:A preliminary report[J].DIMACS Technical Reports,1995,95(7):1-9.

[6]徐寶根.關(guān)于連通圖的IC-著色[J].華東交通大學(xué)學(xué)報,2006,23(1):134-136.

[7]SHIUE C L,FU H L.The IC-indices of complete bipartite graphs[J].The Electronic Journal of Combinatorics,2008,15(3):1-13.

[8]陳劍峰.笛卡爾積圖Pm×Pn的IC-著色[J].莆田學(xué)院學(xué)報,2011,18(2):13-15.

[9]陳劍峰.星的細分圖的IC-著色[J].莆田學(xué)院學(xué)報,2012,19(2):11-13.

[10]周娟,謝承旺,徐寶根.關(guān)于圈Cn的IC-著色和IC-指數(shù)[J].華東交通大學(xué)學(xué)報,2012,29(4):64-68.

[11]陳劍峰,楊大慶.雙星圖的IC-著色[J].純粹數(shù)學(xué)與應(yīng)用數(shù)學(xué),2012,28(2):201-212.

[12]陳劍峰,楊大慶.雙星圖的IC-指數(shù)[J].數(shù)學(xué)的實踐與認識,2013,43(7):132-140.

IC-coloring and IC-index of Octopus Graphs

Yang Yang,Wang Ligong
(Department of Applied Mathematics,School of Science,Northwestern Polytechnical University,Xi'an 710072,China)

The octopus graphH(Cm,n)is formed by identifying a vertex of the cycleCmand the center of a starSTn=K1,n.In this paper,the problem of IC-colorings on the octopus graph is studied.Whenm=3,4,5,n≥1,IC-indices andmaximal IC-colorings of the octopus graphH(Cm,n)are obtained respectively.A conjecture for the up?per bound of the IC-index of the octopus graph is proposed.

IC-coloring;IC-index;octopus graph

O157.5

A

2014-01-10

國家自然科學(xué)基金（11171273）；國家級大學(xué)生創(chuàng)新創(chuàng)業(yè)訓(xùn)練計劃項目資助（201310699069）

楊楊（1990—），男，碩士研究生，研究方向為圖論；王力工（1968—），男，教授，博士生導(dǎo)師，研究方向為圖論及應(yīng)用。

1005-0523（2014）04-0077-05