往復旋轉直線運動球軸承保持架的強度分析

馬延波，孫立明，傅建海，曾獻智，宗曉明

(1.洛陽軸研科技股份有限公司，河南 洛陽 471039；2.萬向錢潮股份有限公司，杭州 311215)

往復旋轉直線運動球軸承(以下簡稱直線軸承)是直線軸承的一種，其基本結構由內圈、外圈、鋼球及保持架組成，可同時做軸向往復運動及周向旋轉運動。該軸承生產成本低、摩擦因數小、精度高、可承受中等強度載荷，是機電設備中關鍵部件之一，廣泛應用于數控機床、自動儀表、沖壓模具及汽車工業等領域[1-2]。

為滿足軸承承載能力的要求，設計中往往需要較多的鋼球個數，這就制約了保持架的強度，一旦保持架強度不夠，就會發生斷裂，造成軸承失效。因此需對保持架進行受力分析，以保證其強度和工作可靠性。由于保持架實際運動狀態比較復雜，難以建立準確的分析模型，因此選取保持架極限運動狀態下的受力進行分析具有典型意義(其他運動狀態下保持架的受力情況均好于該極限運動狀態)。文中以某機構用直線軸承為例，對其保持架在極限運動狀態下的受力情況進行有限元仿真分析，以校核保持架的強度。

1 軸承工況及結構特點

某直線軸承如圖1所示。該結構中空心轉軸充當軸承內圈，直線軸承有軸向限位裝置。內圈相對外圈轉速為60 r/min，軸向往復運動頻率為16 Hz，往復運動行程為5 mm，徑向載荷為300 N，球組節圓直徑為25 mm，鋼球直徑為3.5 mm，保持架兜孔直徑為3.75 mm。保持架兜孔在圓周上呈螺旋線分布，圓周均布18列，每列3個鋼球。

圖1 直線軸承

2 保持架受力分析

該軸承在做直線及旋轉運動時，保持架受到鋼球施加的沿軸向和旋轉運動切線方向的作用力(由鋼球與滾道間的摩擦力提供)。在正常運動情況下，保持架兜孔受到的鋼球作用力較小。但實際工作中，保持架可能出現極限運動狀態，即保持架端面與軸承的軸向限位裝置接觸，導致保持架不能運動，鋼球與滾道變為純滑動。此時，鋼球對兜孔的作用力最大，為2fq(內、外滾道同時對鋼球施加大小、方向相同的摩擦力fq)。

根據Hertz接觸理論，接觸載荷與鋼球位置角的關系為[3]

Qq=QmaxcosnΨq,

(1)

式中：Qq為內、外接觸角相等時第q個鋼球與滾道間的接觸載荷；q為鋼球序號，規定位于徑向載荷作用線上的鋼球序號為0，兩邊對稱，依次為1，2，3，…；Qmax為最大滾動體載荷；n為指數，對于點接觸n=1.5；Ψq為第q個鋼球的位置角，如圖2所示。

圖2 軸承接觸載荷及鋼球位置角示意圖

考慮正常徑向游隙時，最大滾動體載荷為

Qmax=5Fr/Z，

(2)

式中：Fr為外部徑向載荷；Z為鋼球個數。

結合(1)～(2)式得，直線軸承運動過程中鋼球與滾道之間所產生的摩擦力fq為

(3)

式中：μ為摩擦因數。

由于軸承同時作旋轉及直線運動，鋼球對兜孔作用力的方向由旋轉運動與直線運動的合力決定，即

(4)

式中：α為兜孔受力方向與水平方向夾角；v為直線運動瞬時速度；Ω為旋轉運動線速度。

根據材料特性選取摩擦因數μ=0.2[4]，由(3)式得，保持架極限狀態下Ψq=0，±20°，±40°，±60°，±80°處兜孔所受作用力2fq依次為11.2，10，7.4，4，0.8 N。由(4)式得兜孔受力方向與水平方向夾角α=45°。

3 保持架有限元分析

3.1 模型建立

仿真時不考慮鋼球離心力的作用(離心力為0.000 02 N，忽略不計)，在SolidWorks中建模，如圖3所示。

圖3 保持架模型

3.2 材料設置

軸承內、外圈及鋼球材料均為G95Cr18鋼，保持架材料為聚酰亞胺。根據材料性質，在SolidWorks中添加聚酰亞胺為自定義材料，并將兩種材料分別應用于對應的三維模型，材料性能見表1。

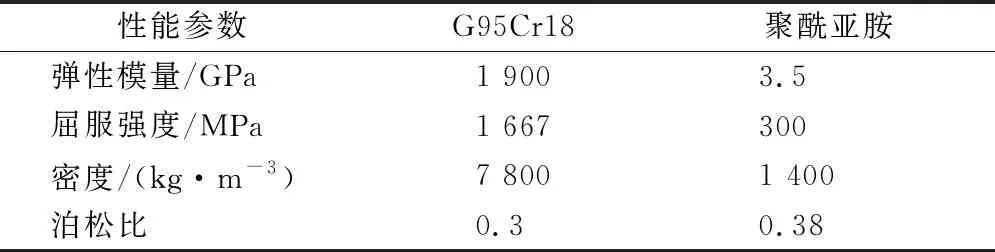
表1 G95Cr18及聚酰亞胺材料性能

3.3 添加固定幾何體

啟動SolidWorks Simulation，選取保持架一端面為固定幾何體，如圖4所示。

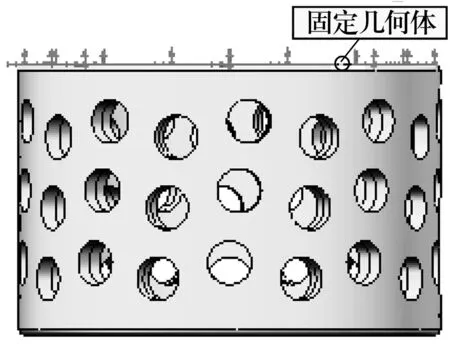
圖4 固定面設置

3.4 添加外部載荷

由球組節圓建立鋼球與保持架兜孔的接觸點。任選一兜孔，建立基準軸1，該軸過鋼球中心，與水平方向成45°。基準軸1與交線圓的交點即為鋼球與兜孔的接觸點，以鋼球與兜孔的接觸點作為力的參考點，添加大小為11.2 N的力，方向類型為“選定的方向”，并選取基準軸1作為力的方向，如圖5所示。

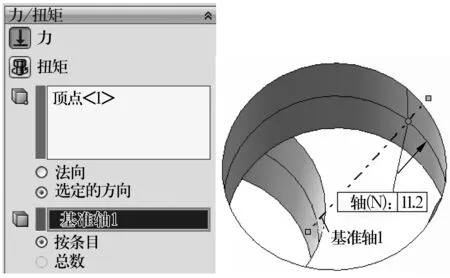
圖5 外部載荷設置

以被選取的兜孔所在兜孔列為0位置角兜孔列，鋼球在同一列兜孔上的作用力大小相等。按以上方法依次對0位置角其余兩兜孔添加大小相等的外部載荷，并以該列為基準，對位置角為±20°，±40°，±60°，±80°的兜孔列添加載荷，載荷值見表2。

表2 載荷值表

3.5 網格化分

對模型進行網格劃分，設置網格大小為0.478 mm。該模型包括401 482個單元，596 104個節點。

3.6 結果分析

從圖6a中可以看出，最大Von Mises應力出現在0位置角鋼球與兜孔接觸點處，應力值為32.8 MPa，遠小于保持架材料的屈服應力300 MPa；并且同一列兜孔所受應力大小相等，0位置角兩側各列兜孔所受應力值逐漸減小，與實際受力情況相符。從圖6b中可以看出，保持架最大變形量只有0.03 mm。

圖6 仿真分析結果

4 結束語

對某機構用往復旋轉直線運動球軸承極限工況下保持架的有限元分析可知，保持架所受最大Von Mises應力遠小于保持架材料的屈服應力，且保持架最大變形量只有0.03 mm，保持架強度滿足要求，安全可靠。