可傾瓦氣體軸承氣膜厚度的計算和分析

程進杰，孫郁，孫立佳，季偉，張武,2

(1.中國科學院 理化技術研究所，北京 100190，2.航天低溫推進劑技術國家重點實驗室，北京 100028)

符號說明

b——軸承寬度，m

B——軸瓦厚度，m

Cb——半徑間隙，m

Cp——名義半徑間隙，m

d——轉子內徑，m

ex——軸心在x坐標上的值，m

ey——軸心在y坐標上的值，m

E——轉子的彈性模量，GPa

f——密度分布概率

F——動壓氣膜力作用在軸瓦上力的矢量

h——氣膜厚度，m

hm——平均氣膜厚度，m

h(θ)——θ方向上的氣膜厚度，m

I——截面慣性矩，m4

K——剛度矩陣

M——彎矩，N·m

Oj——軸心位置

Opad——軸瓦中心位置

P——氣膜壓力，Pa

rg——離心力引起的軸的變形量，m

R——軸半徑，m

R0——初始狀態下的軸半徑，m

Rb0——初始狀態下的支點圓半徑，m

Rbearing——支點圓半徑，m

Rp0——初始狀態下的瓦半徑，m

Rpad——軸瓦半徑，m

S——軸瓦弧長，m

t——時間，s

v——軸頸表面的周向運動速度，m/s

αp——線脹系數，℃-1

β——軸承偏斜角度，rad

βi——第i軸瓦的支點位置角，rad

ΔTp,ΔTs——軸瓦和軸的溫差，℃

λ——軸承的偏斜程度

δ1——軸瓦半徑的膨脹變形，m

δ2——軸瓦厚度的變化量，m

δ3——軸的熱變形量，m

δ4——軸瓦的彈性變形量，m

δi——軸瓦的擺角，rad

δtotal(θ)——在考慮軸瓦和軸的熱力變形時，θ方向上氣膜厚度的變化量，m

ε0——轉子在中心平面的偏心率

θ——沿軸承軸向的角坐標，rad

λe——軸承的偏斜率

λm——軸承的最大偏斜率

μ——氣體的動力黏度，Pa·s

ν——泊松比

ρ——軸密度，kg/m3

σ——表面粗糙度的標準差

φ——軸承軸向上軸的偏心角，(°)

φ0——偏斜條件下的姿態角，(°)

ψ——承載方向的偏斜平面和軸向平面的夾角，(°)

ω——軸的轉速，r/min

1 概述

相對于傳統的滾動軸承和滑動軸承，氣體軸承具有轉速高、摩擦損失小、壽命長、噪聲低、無污染和工作溫度范圍廣等優點，在很多領域得到了廣泛應用，如透平膨脹機、高速牙鉆、高速主軸、慣性陀螺儀等。

根據氣膜壓力產生的原理,氣體軸承大致分為擠壓膜氣體軸承、靜壓氣體軸承和動壓氣體軸承3種。動壓氣體軸承由于不需要供氣系統，降低了裝置的復雜性，另外，由于不需要耗費高壓氣體，提高了運行的經濟性，且動壓效果隨表面相對運動速度的增加而愈加明顯[1]。

目前，較為常見的幾種動壓氣體軸承結構形式有可傾瓦型、螺旋槽型、人字槽型、階梯型和箔片型等。可傾瓦軸承由于軸瓦可以繞樞軸擺動，各軸瓦均能自由傾斜，具有良好的穩定性和自對中能力，在旋轉機械中得到了廣泛應用，特別是在高速透平機械中日益受到青睞。

可傾瓦氣體軸承一般由多片可繞其樞軸自由旋轉的軸瓦構成，結構如圖1所示，為了便于顯示，放大了軸和軸瓦的間隙。當系統承受載荷時，每片軸瓦都會根據載荷補償氣膜厚度的改變，并產生相應的氣膜壓力保持平衡，以達到穩定狀態。

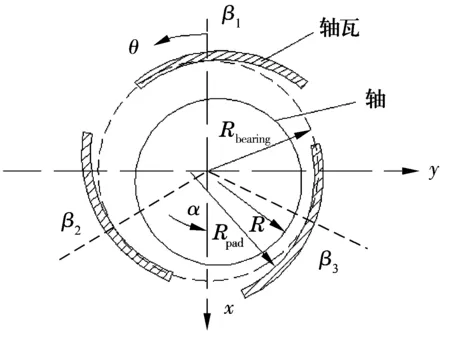
圖1 可傾瓦動壓氣體軸承結構簡圖

目前主要研究的是可傾瓦油潤滑軸承，對可傾瓦氣體軸承的研究相對較少。而且研究的方向主要側重于軸承的穩定性、剛度、阻尼系數、承載力、偏斜比和偏心比等方面，很少涉及到熱力變形、軸線偏斜、離心變形和表面粗糙度等結構參數。由于氣體軸承的半徑間隙很小(0.02 mm左右)，高轉速下這些影響因素不可忽略[2]。

2 基礎理論

氣體潤滑軸承的動靜性能計算均會涉及到Reynolds方程的求解，求解該方程首先需要求解氣膜厚度，忽略氣體動力黏度隨溫度的變化，等溫條件下的氣體潤滑Reynolds方程為

(1)

氣膜厚度的計算公式為[2]

h=Cp-(Cp-Cb)cos(θ-βi)-(R+

B)δisin(θ-βi)+excosθ+eysinθ。

(2)

然而可傾瓦氣體軸承很少能夠在理想狀態下運行，實際運行中的離心力變形、軸瓦和軸的熱力變形、制造和安裝誤差等，都會影響軸承的氣膜厚度。

3 氣膜厚度的影響因素

研究的可傾瓦氣體軸承結構尺寸如下：軸徑為25 mm，材料為鋁合金；軸瓦厚度為2 mm，寬為30 mm，內半徑為15 mm，材料為3Cr13;半徑間隙為0.02 mm，支點圓半徑為12.5 mm。

下文將分別計算離心力造成的軸的徑向變形、軸瓦和軸的熱變形、軸瓦的彈性變形以及軸承偏斜和表面粗糙度對氣膜厚度的影響。

3.1 離心力變形

轉子在旋轉時由于離心力的存在，會造成軸的徑向變形，變形量為[3]

(3)

C0=[(3+ν)/8]ρω2(d2+R2)；C1=-[(3+ν)/8]ρω2d2R2；E=72 GPa；ν=0.33；ρ=2 820 kg/m3。

由(3)式可知，離心力變形量與轉速的平方成正比，且和轉子半徑的立方有很大相關性，因此轉子的轉速和直徑也是可傾瓦軸承設計中需要考慮的因素。對于轉速較低的場合，可以忽略離心力導致的變形，但在高轉速下，離心力導致的變形不可忽略。

對于直徑為25 mm的軸，當轉速為12×104r/min時，離心力變形為0.5 μm；轉速為20×104r/min時，離心力變形為1.67 μm。由此可知，一般情況下，轉速對軸離心力變形的影響可以忽略。

為了減輕軸的質量，提高軸承承載力，有時會采用空心軸。假設有2個空心軸，內徑分別為15 mm和20 mm，外徑均為25 mm。轉速為12×104r/min時，離心力變形分別為1.1 μm和1.47 μm；轉速為20×104r/min時，離心力變形分別為3 μm和4.1 μm。由此可知，雖然空心軸可以減小軸的質量，但是會導致軸的離心力變形量增大。因此采用空心軸時，需要充分考慮軸承結構尺寸對其離心力變形的影響。

3.2 熱變形[4]

可傾瓦氣體軸承在運行時，氣膜受到摩擦而造成溫升，一般情況下，這些熱量會通過軸和軸瓦傳遞到周圍環境中并且會隨著軸的轉動從氣膜中排出。軸、軸瓦以及氣膜的溫度，與軸承的結構和轉子的轉速關系密切，一般是通過對氣膜建立瞬態能量求解，再用瞬態導熱方程計算軸和軸瓦的溫度分布[5]。

假設氣膜、軸瓦以及軸的溫度一致，求解由于溫升而導致的軸和軸瓦的熱變形。軸瓦的熱變形包括軸瓦的厚度變化和軸瓦曲率半徑的變化，而軸的半徑也會發生變化。這些變化會影響半徑間隙和最小氣膜厚度，從而影響軸承的性能。

(1)軸瓦的半徑膨脹變形量為

δ1=αpRpΔTp，

(4)

對于3Cr13，αp=10-5/℃，Rp=15 mm；假設溫差為20 ℃，可得變形量為3 μm。由此可知，溫度的升高對名義半徑間隙的影響較大，在可傾瓦結構設計中，應該充分考慮到運行中的溫升問題。

(2)軸瓦厚度的變化量為

δ2=αpBΔTp，

(5)

對于3Cr13，αp=10-5℃，B=2 mm，假設溫差為20 ℃，則變形量為0.4 μm。

(3)軸的熱變形為

δ3=αpRΔTs，

(6)

對于鋁合金，αp=2.45×10-5/℃，R=12.5 mm，假設溫差為20 ℃，則變形量為6.1 μm。

3.3 彈性變形

對于可傾瓦油潤滑軸承，由于載荷較大，在設計時需要考慮軸瓦的彈性變形。對于氣體軸承，一般載荷較小，作用在軸瓦上的力較小，但為了減小軸瓦的慣性力以及支點處的摩擦力，一般情況下軸瓦的厚度較薄且質量較輕，有的甚至采用彈性軸瓦，因此在設計過程中需要考慮其彈性變形。軸瓦的簡化結構如圖2所示，假設支點為剛性軸承，則軸瓦的彈性變形[5]為

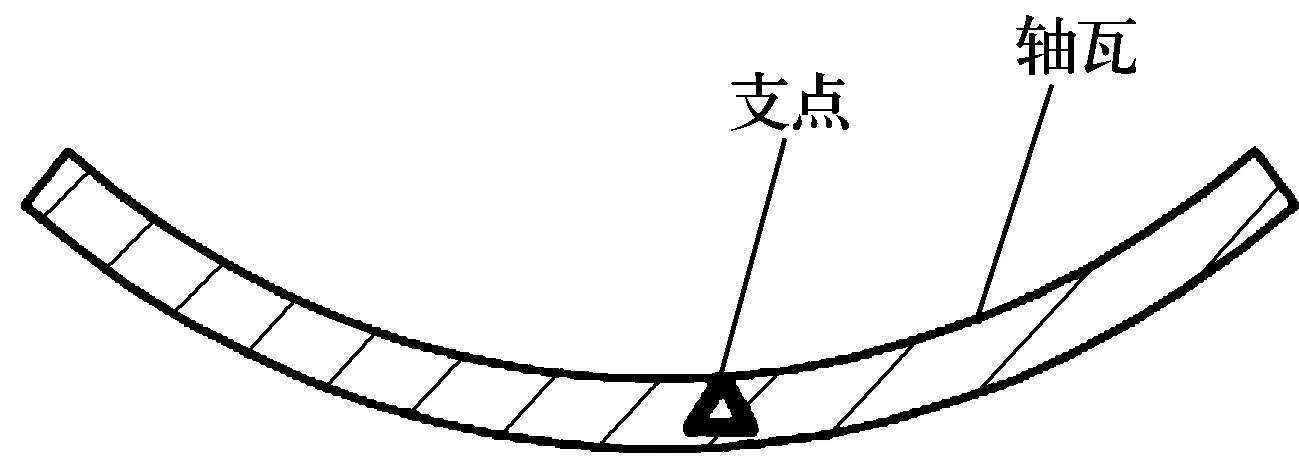
圖2 軸瓦結構簡圖

K·δ4=F。

(7)

3.4 軸承偏斜

對于軸承-轉子系統，軸承的偏斜會影響潤滑膜內的壓力分布、承載能力和氣膜厚度等，從而影響軸承系統的穩定性。對于流體潤滑軸承，即使設計非常好，由于存在制造和裝配誤差，轉子很少能夠在對中條件下運行，轉子的偏斜運動常常是由制造裝配誤差、偏心承載、軸的熱變形和彈性變形或者外部的沖擊所致。由于可傾瓦分為線接觸和點接觸，對于線接觸，軸瓦只有1個自由度，只能沿軸線擺動；對于點接觸，軸瓦有2個自由度，還可以在軸向上擺動。文中分析的為線接觸可傾瓦軸承。線接觸可傾瓦軸承的偏斜分為2種類型：豎直偏斜和水平偏斜，通常軸承偏斜由這2種類型混合而成[6]。

z為軸承中心的軸向坐標；y為垂直于軸承中心，在豎直方向的坐標；x為垂直于軸承中心，在水平方向的坐標。

豎直偏斜：在yz平面內，軸的軸向和軸承的軸向的夾角如圖3所示。

圖3 豎直偏斜

水平偏斜：在xz平面內，軸的軸向和軸承的軸向的夾角如圖4所示。

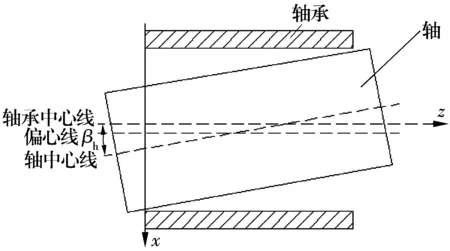
圖4 水平偏斜

偏斜狀態下滑動軸承的結構如圖5所示，λ的值在0～1之間，ε0，φ，ψ詳細內容可參考文獻[8-9]。

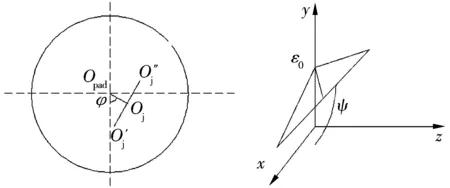
圖5 偏斜滑動軸承的結構

λ=λe/λm，

(8)

cos(ψ-φ0),

(9)

λe=2βb/Cp。

(10)

3.5 表面粗糙度

在絕大多數關于可傾瓦滑動軸承的研究中，都是假設軸承-轉子表面為光滑表面，然而，當表面粗糙度和潤滑膜的尺寸在一個數量級時，需要考慮到潤滑表面粗糙度。表面粗糙度的存在使軸和軸承的安全運行間隙減小了，更容易發生碰磨，表面粗糙度的隨機模型是由Christensen提出的[9]。

潤滑膜的厚度為

h=hm(x,y,z)+δ(x,y,z)，

(11)

δ(x,y,z)為軸承表面任一點的厚度與平均厚度之差，可以為正值也可以為負值。期望因子E(x)定義為

(12)

由于絕大多數的機械表面服從Gauss分布，用多項式形式隨機變量的密度分布模擬Gauss分布

(13)

式中：c=3σ為隨機潤滑膜厚度變化的一半。考慮軸和軸承表面粗糙度，并假設兩者相等，表面粗糙度使實際可安全運行的間隙減小了6σ。如標準粗糙度為0.8，則由于2個摩擦面粗糙度造成的運行間隙的減小量為4.8 μm。因此在可傾瓦軸承設計時，需要充分考慮表面粗糙度的影響。

結合(12)～(14)式，潤滑膜厚度的期望值為

(14)

由此可知，表面粗糙度的存在并不影響潤滑膜的平均厚度，也就是說，不會影響名義半徑間隙。但是由于表面不光滑，軸承和軸在運行過程中容易發生碰磨，使安全運行的最小潤滑厚度增大。另外有研究顯示，表面粗糙度還會影響壓力分布和承載能力等。

3.6 修正后的氣膜厚度

考慮熱變形、離心變形和彈性變形后氣膜厚度及其變化量計算公式為

h(θ)=Cp0-(Cp0-Cb0)cos(θ-βi)-(R+

B)δisin(θ-βi)+excosθ+eysinθ+Cpλλm·

(15)

δtotal(θ)=(δ1+δ4-rg-δ3)-(δ1+δ4+

δ2)cos(θ-βi) 。

(16)

從上式可知，軸瓦的半徑變化和彈性變形使氣膜間隙增大；離心力變形、軸瓦厚度方向的熱變形以及軸的熱變形使氣膜間隙減小；表面粗糙度和軸承的偏斜使安全運行的最小間隙增大，并且氣膜在軸向上的厚度分布也是變化的。因此在可傾瓦的設計中，要綜合考慮到各種影響因素。把影響軸承性能的主要因素控制在合理的范圍以內是可傾瓦設計的關鍵點之一。

4 結論

相對于固定瓦軸承，可傾瓦軸承的設計制造難度較高，在不同運行條件下，對可傾瓦的結構尺寸的變化進行分析，得出如下結論：

(1)在轉速不高且為實心軸的情況下，軸半徑對離心力變形的影響較小，但是對于空心軸，需要考慮軸承結構尺寸對離心力變形的影響。

(2)溫度的升高對軸瓦厚度的影響較小，而對軸瓦的名義半徑和軸半徑的影響較大。

(3)通常情況下，可傾瓦氣體軸承承載力小，軸瓦的彈性變形可以忽略，但是對于彈性軸瓦，需要考慮其彈性變形。

(4)軸承的偏斜使氣膜厚度在軸向上不再是一個定值，并且會影響軸承的安全運行。

(5)表面粗糙度的存在并不影響潤滑膜的平均厚度，但是會使安全運行的最小氣膜厚度增大。