基于Kalman濾波和譜峭度的滾動(dòng)軸承故障診斷

劉志川，唐力偉，曹立軍

(軍械工程學(xué)院 火炮工程系，石家莊 050003)

滾動(dòng)軸承廣泛應(yīng)用于旋轉(zhuǎn)機(jī)械中，是常見(jiàn)的易損件。軸承故障會(huì)導(dǎo)致機(jī)器出現(xiàn)振動(dòng)和噪聲，嚴(yán)重時(shí)會(huì)影響整臺(tái)設(shè)備的正常運(yùn)行，因此軸承的狀態(tài)檢測(cè)和故障診斷具有重要意義。

共振解調(diào)技術(shù)是目前軸承故障診斷中普遍使用的方法，但是存在帶通濾波器參數(shù)難以確定的問(wèn)題，傳統(tǒng)的小波和小波包分析技術(shù)均不能自適應(yīng)選擇最優(yōu)帶通，導(dǎo)致應(yīng)用受限。譜峭度[1]的基本原理是通過(guò)計(jì)算頻域中每根譜線的峭度值，從而在頻域中定位瞬態(tài)沖擊。文獻(xiàn)[2]提出將譜峭度值作為短時(shí)Fourier窗口函數(shù)，通過(guò)譜峭度圖選擇帶通濾波器的參數(shù)。針對(duì)譜峭度圖計(jì)算耗時(shí)的問(wèn)題，文獻(xiàn)[3]提出了快速譜峭度圖的概念。文獻(xiàn)[4]則指出在信噪比較高的情況下，譜峭度能夠較好地識(shí)別瞬態(tài)沖擊信號(hào)。軸承工作環(huán)境相對(duì)復(fù)雜，環(huán)境噪聲較大，而復(fù)雜工況對(duì)譜峭度計(jì)算值會(huì)產(chǎn)生影響，從而給最優(yōu)帶通濾波的帶寬和中心頻率的計(jì)算帶來(lái)誤差，影響診斷效果，因此有必要對(duì)信號(hào)進(jìn)行降噪預(yù)處理。

Kalman濾波是一種動(dòng)態(tài)數(shù)據(jù)處理方法，屬于遞推式濾波方法[5]，可以克服傳統(tǒng)時(shí)頻分析方法不適用于處理非平穩(wěn)信號(hào)的問(wèn)題，對(duì)測(cè)量數(shù)據(jù)逐一處理，由遞推方程隨時(shí)給出某一時(shí)刻新的狀態(tài)估計(jì)值，并與該時(shí)刻后的數(shù)據(jù)一起做出下一狀態(tài)的最優(yōu)估計(jì)，達(dá)到信號(hào)降噪目的。在此，針對(duì)軸承內(nèi)、外圈裂紋故障，將Kalman濾波與快速譜峭度圖相結(jié)合，以實(shí)現(xiàn)軸承的故障診斷。

1 AR模型

1.1 參數(shù)估計(jì)

對(duì)于時(shí)間序列{xt}，t=1，2，…,N，AR模型為

xt=φ1xt-1+φ2xt-2+…+φnxt-n+at，

(1)

式中：φ2,…，φn及σa是AR模型[6]的參數(shù);n為模型階次。參數(shù)估計(jì)即估計(jì)出這n+1個(gè)數(shù)值，由于

at=xt-φ1xt-1-φ2xt-2-…-φnxt-n，

(2)

(3)

1.2 模型階數(shù)

AR模型的階次n未知，需要在遞推過(guò)程中確定。在遞推過(guò)程中，可以給出低階到高階的每一組參數(shù)，模型的最小預(yù)測(cè)誤差功率P是遞減的，當(dāng)Pn達(dá)到最小值或者不再變化時(shí)，此時(shí)的階次就是AR模型的正確階次。

定階是建立AR模型的關(guān)鍵過(guò)程，其中AIC準(zhǔn)則(Akaike Information Criterion)應(yīng)用較為廣泛。它由2項(xiàng)構(gòu)成：第1項(xiàng)隨階數(shù)增大而變小，體現(xiàn)模型擬合好壞；第2項(xiàng)隨階數(shù)增大而變大，體現(xiàn)模型參數(shù)多少。AIC準(zhǔn)則表示為

AIC(n)=Nln(Pn)+2n。

(4)

從n=0開(kāi)始增加模型階數(shù)，AIC(n)先減小,后增大。當(dāng)階數(shù)n達(dá)到某一值n0時(shí)，AIC(n0)最小，則n0即為AR模型的最合適階次。

2 Kalman濾波

Kalman濾波是工程應(yīng)用較為成熟的一種遞推線性最小方差估計(jì)，能夠通過(guò)前一時(shí)刻的最優(yōu)值與當(dāng)前時(shí)刻的測(cè)量值一起給出當(dāng)前時(shí)刻的最優(yōu)估計(jì)，能夠?qū)y(cè)量數(shù)據(jù)進(jìn)行實(shí)時(shí)更新。通過(guò)對(duì)原始數(shù)據(jù)建立的AR模型可以構(gòu)建Kalman濾波的5個(gè)基本方程。

設(shè)齒輪箱振動(dòng)真實(shí)信號(hào)為x(t),t=1,2,3,…，N，觀測(cè)噪聲為R，觀測(cè)值為y(t)，則觀測(cè)方程可表示為

y(t)=Hx(t)+R,

(5)

其中H=[1 0 … 0]1×n。設(shè)系統(tǒng)狀態(tài)為s(t)=[x(t),x(t-1),…,x(t-n+1)]T，則狀態(tài)轉(zhuǎn)移方程可表示為

s(t)=As(t-1)+a(t)，

(6)

其中In-1為n-1維單位陣。由此可建立Kalman濾波的5個(gè)基本方程：

(1)假設(shè)系統(tǒng)現(xiàn)在狀態(tài)為t，根據(jù)上一時(shí)刻狀態(tài)預(yù)測(cè)現(xiàn)在的狀態(tài)為

s(t|t-1)=As(t-1|t-1)+a(t);

(7)

(2)s(t|t-1)時(shí)刻協(xié)方差更新為

P(t|t-1)=AP(t-1|t-1)A′+Q;

(8)

(3)更新Kalman增益為

K(t)=P(t|t-1)H′/[HP(t|t-1)H′+R];

(9)

(4)新觀測(cè)得到的狀態(tài)最優(yōu)估計(jì)值為

s(t|t)=X(t|t-1)+K(t)[y(t)-

Hs(t|t-1)];

(10)

(5)s(t|t)時(shí)刻協(xié)方差更新為

P(t|t)=[I-K(t)H]P(t|t-1),

(11)

式中：P為協(xié)方差；Q為系統(tǒng)過(guò)程噪聲；R為測(cè)量噪聲；K(t)為系統(tǒng)增益；I為單位矩陣。

3 譜峭度

信號(hào)的Wold-Cramer分解在頻域的表達(dá)式為

(12)

式中：H(t,f)為t時(shí)刻沖擊響應(yīng)h(t,f)的頻域表示，是一個(gè)復(fù)包絡(luò)函數(shù)。

定義Y(t)過(guò)程的4階譜累積量為

(13)

2n階的譜瞬時(shí)矩為

S2nY(f)E{|H(t,f)dX(f)|2n}/df。

(14)

則譜峭度定義為

譜峭度[7-8]是關(guān)于中心頻率和帶寬的函數(shù)，當(dāng)帶寬無(wú)限小時(shí)，譜峭度為0，當(dāng)帶寬過(guò)大時(shí)，譜峭度無(wú)法反映頻帶范圍中的瞬態(tài)沖擊現(xiàn)象。快速譜峭度圖的原理是找到一個(gè)中心頻率fs和帶寬Bw，使峭度達(dá)到最大值，這時(shí)對(duì)應(yīng)的中心頻率和帶寬即最優(yōu)濾波器的2個(gè)參數(shù)。快速譜度圖是平面上的二維圖，圖中顏色的深淺代表不同中心頻率和帶寬組合下的峭度值，顏色最深處峭度值最大，對(duì)應(yīng)獲得最優(yōu)濾波器的中心頻率和帶寬。

4 基于Kalman濾波和譜峭度的故障診斷方法

軸承工作環(huán)境常常有較大噪聲，為降低振動(dòng)信號(hào)噪聲，提高故障特征，先采用Kalman濾波技術(shù)對(duì)振動(dòng)信號(hào)進(jìn)行降噪預(yù)處理，然后利用快速譜峭度圖確定最優(yōu)濾波器的中心頻率和帶寬。應(yīng)用能量算子解調(diào)法解決傳統(tǒng)Hilbert包絡(luò)解調(diào)過(guò)程中存在的信號(hào)兩端調(diào)制和計(jì)算量大的問(wèn)題，然后對(duì)包絡(luò)進(jìn)行FFT變換得到包絡(luò)譜，將包絡(luò)譜中峰值較大的頻率成分與軸承故障特征頻率相比較，實(shí)現(xiàn)診斷，其流程如圖1所示。

圖1 軸承故障診斷方法流程圖

5 試驗(yàn)驗(yàn)證

軸承內(nèi)、外圈故障實(shí)測(cè)信號(hào)來(lái)自二級(jí)減速器試驗(yàn)平臺(tái)，試驗(yàn)軸承為6206型深溝球軸承，鋼球個(gè)數(shù)Z=9，鋼球直徑Dw=9.5 mm，球組節(jié)圓直徑Dpw=46.5 mm。采用線切割分別在軸承的內(nèi)圈和外圈上加工寬度0.5 mm、深度1 mm的細(xì)小裂紋作為故障。采集信號(hào)時(shí)，振動(dòng)加速度傳感器B&K4508固定在故障軸承所在的軸承座上，采樣頻率為10 kHz；轉(zhuǎn)速由JN338型轉(zhuǎn)速轉(zhuǎn)矩傳感器測(cè)量。

5.1 內(nèi)圈故障

輸入軸轉(zhuǎn)速為610.20 r/min，故障頻率f=27.55 Hz，中間軸轉(zhuǎn)動(dòng)頻率fr=5.08 Hz，采樣時(shí)間為2.5 s。

首先通過(guò)原始信號(hào)建立系統(tǒng)AR模型，利用AIC準(zhǔn)則計(jì)算得到的AIC曲線如圖2所示，從曲線中可以看出，階數(shù)取50時(shí)，AIC有極小值，因此確定模型階數(shù)為50。

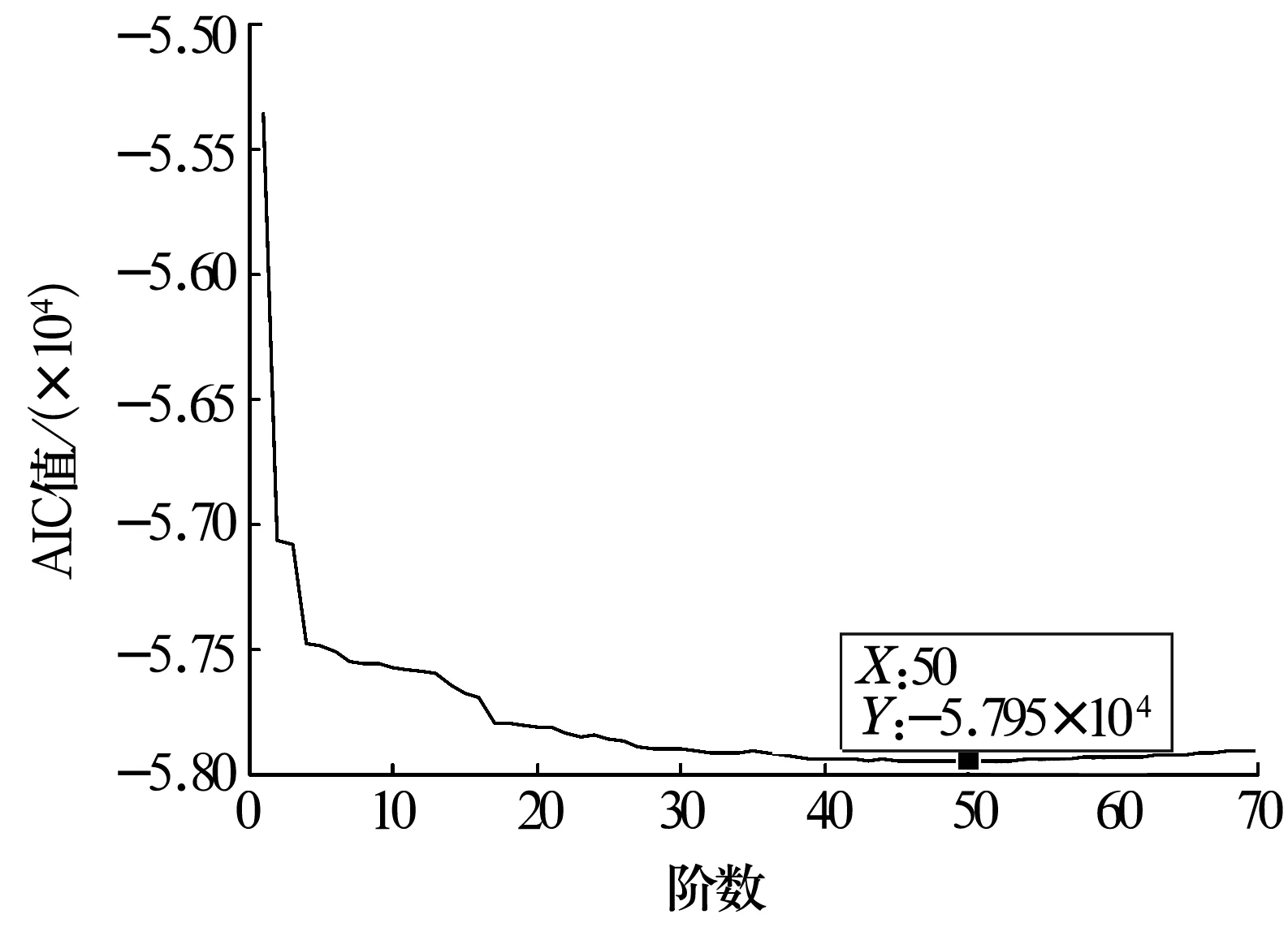
圖2 AR模型的AIC曲線

Kalman濾波過(guò)程中，過(guò)程噪聲和觀測(cè)噪聲是2個(gè)重要參數(shù)[9]。觀測(cè)噪聲使用小波變換降噪的方法提取，對(duì)振動(dòng)信號(hào)進(jìn)行小波多尺度分解，得到小波系數(shù)，設(shè)置合適的閾值，大于閾值的小波系數(shù)置零，對(duì)保留的小波系數(shù)進(jìn)行逆變換即為噪聲信號(hào)。過(guò)程噪聲在濾波過(guò)程中由大量試驗(yàn)數(shù)據(jù)確定。軸承內(nèi)圈故障信號(hào)濾波前、后的時(shí)域圖如圖3所示，從圖中可以明顯看出，濾波后信號(hào)幅值減小，沖擊更加明顯。

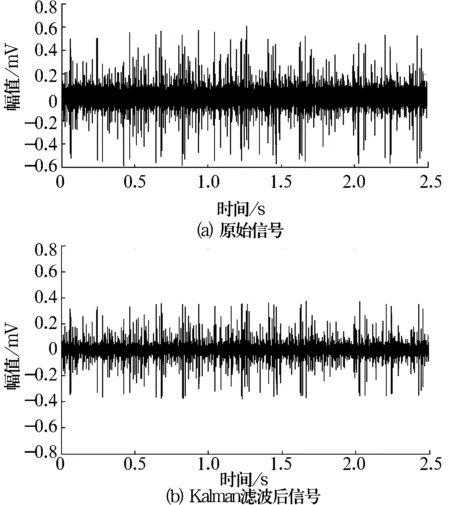
圖3 軸承內(nèi)圈故障信號(hào)濾波前、后時(shí)域圖

對(duì)濾波后的信號(hào)進(jìn)行譜峭度計(jì)算，繪制快速譜峭度圖，如圖4所示。

圖4 濾波后內(nèi)圈故障信號(hào)的快速譜峭度圖

由圖4可知，在中心頻率為4 791.67 Hz、帶寬為416.67 Hz的頻帶內(nèi)，峭度達(dá)到最大值35(在3.6層內(nèi))，其他頻帶信噪比較低。以此中心頻率和帶寬為帶通濾波器的最優(yōu)參數(shù)對(duì)信號(hào)進(jìn)行帶通濾波，并對(duì)帶通濾波后信號(hào)進(jìn)行能量算子包絡(luò)解調(diào)，結(jié)果如圖5所示。圖中可以看出與內(nèi)圈裂紋故障特征頻率接近的27.48 Hz及其倍頻等，而且故障軸承所在軸的轉(zhuǎn)動(dòng)頻率(5.09 Hz)非常明顯，從結(jié)果可以判斷是內(nèi)圈故障。

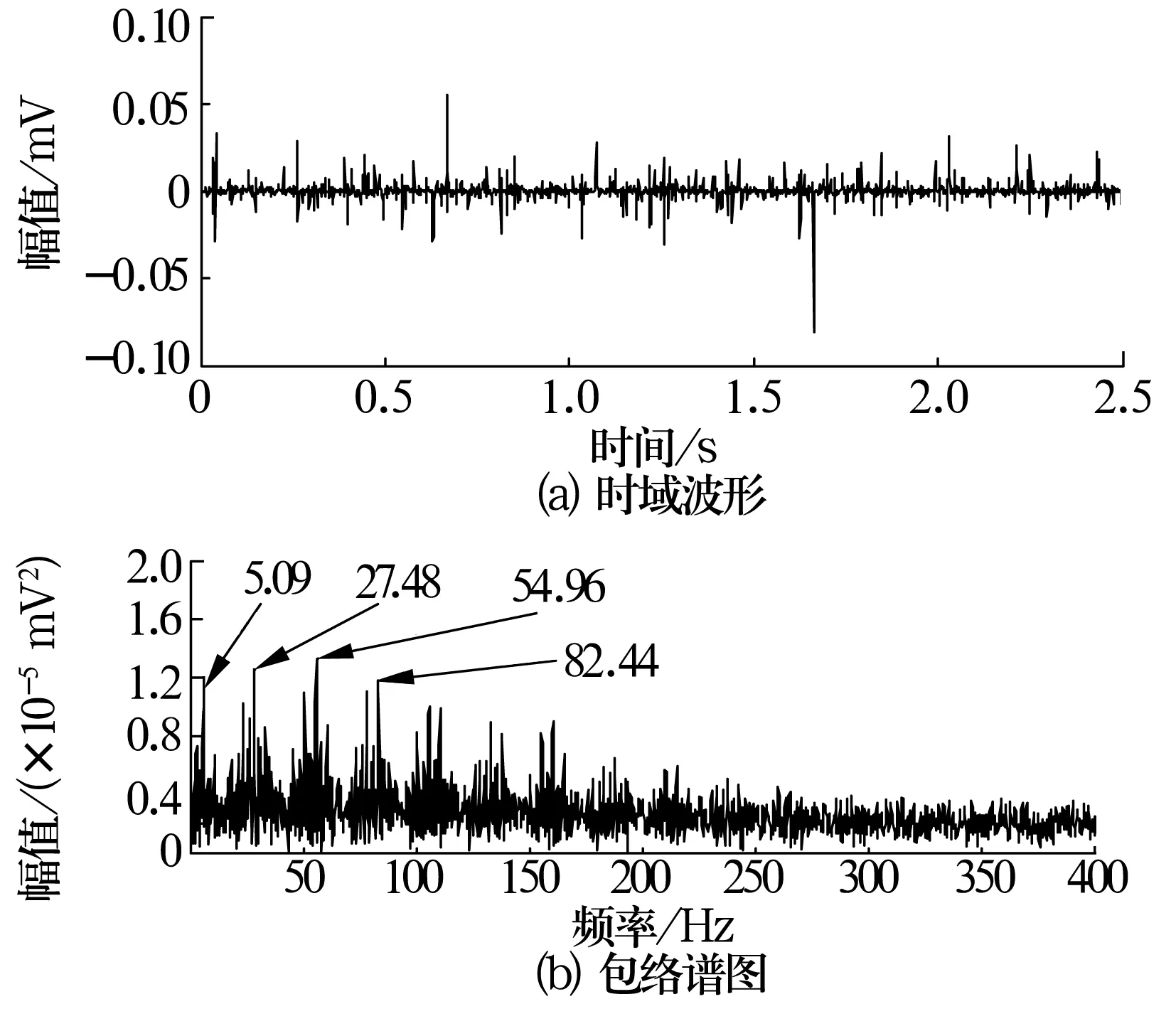
圖5 帶通濾波后內(nèi)圈故障信號(hào)時(shí)頻圖

5.2 外圈故障

輸入軸轉(zhuǎn)速為1 488.5 r/min，故障頻率f=44.41 Hz，中間軸轉(zhuǎn)動(dòng)頻率fr=12.4 Hz，采樣時(shí)間為1 s。對(duì)采集到的信號(hào)進(jìn)行Kalman濾波及譜峭度計(jì)算，繪制的快速譜峭度圖如圖6所示。由圖可知，在中心頻率為4 375 Hz、帶寬為1 250 Hz的頻帶內(nèi)峭度達(dá)到最大值13.6(在2層內(nèi))。對(duì)信號(hào)進(jìn)行帶通濾波和能量算子包絡(luò)解調(diào)，結(jié)果如圖7所示，可以看出與外圈裂紋故障特征頻率接近的44.26 Hz及其倍頻等，而且故障軸承所在軸的轉(zhuǎn)動(dòng)頻率(12.52 Hz)非常明顯，從結(jié)果可以判斷是外圈故障。

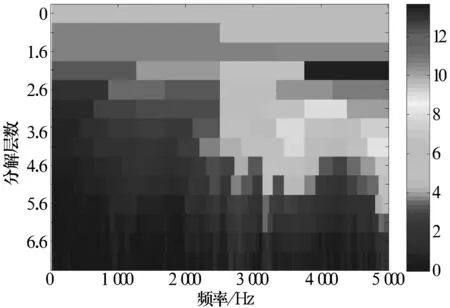
圖6 濾波后外圈故障信號(hào)的快速譜峭度圖

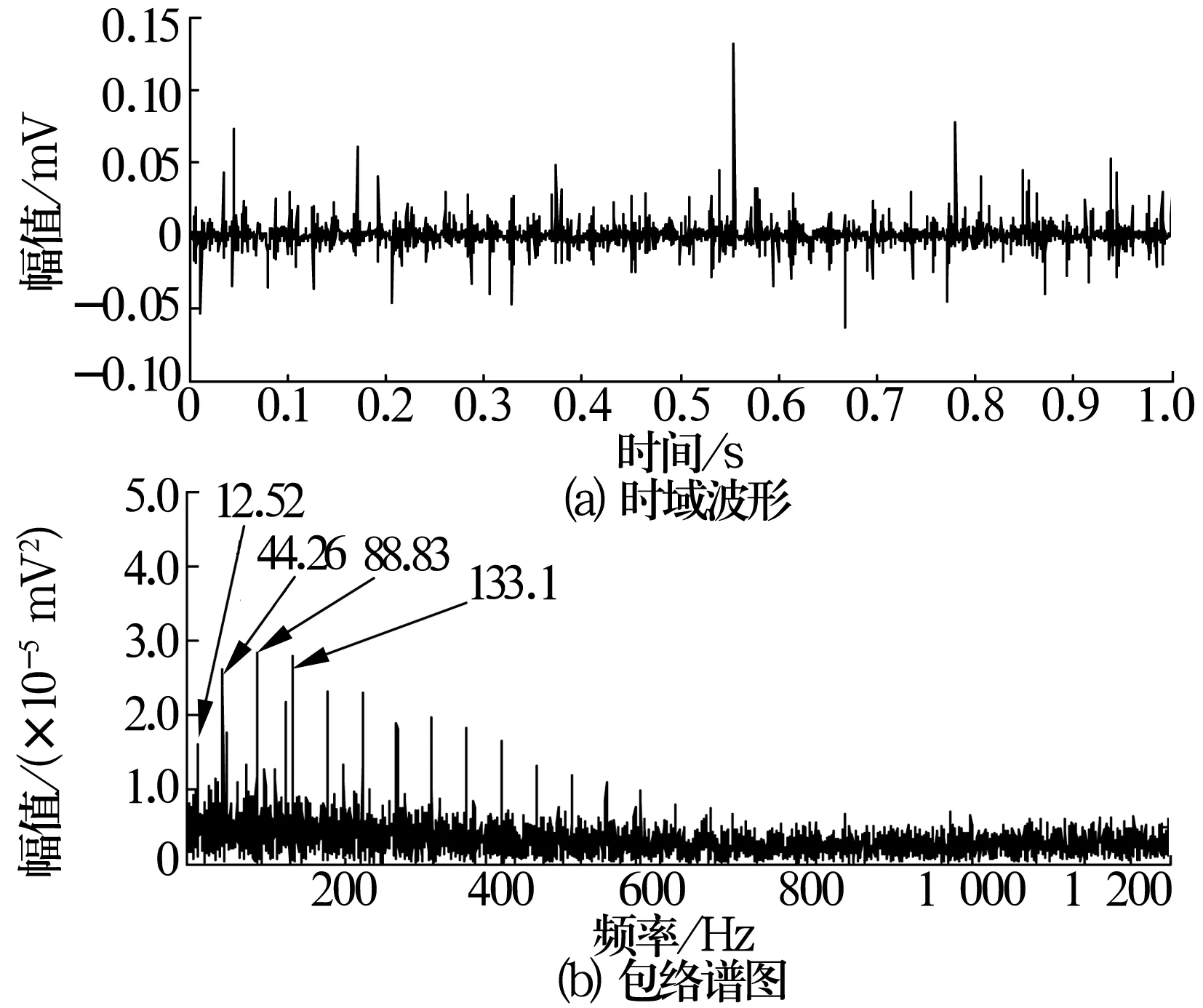
圖7 帶通濾波后外圈故障信號(hào)時(shí)頻圖

6 結(jié)束語(yǔ)

為解決傳統(tǒng)包絡(luò)分析方法中心頻率和帶寬參數(shù)難以確定的問(wèn)題，提出了基于Kalman濾波和譜峭度圖的軸承故障診斷方法。首先建立系統(tǒng)AR模型，對(duì)原始信號(hào)進(jìn)行Kalman濾波降噪預(yù)處理，提高信噪比，然后利用譜峭度自適應(yīng)確定最優(yōu)濾波器的中心頻率和帶寬，最后利用能量算子解調(diào)法對(duì)帶通濾波后的信號(hào)進(jìn)行包絡(luò)解調(diào)分析，結(jié)合軸承故障特征頻率實(shí)現(xiàn)故障診斷。

對(duì)工程信號(hào)的分析處理驗(yàn)證了本方法的可行性，而且在轉(zhuǎn)速相對(duì)較低的情況下也可以成功診斷出軸承內(nèi)、外圈故障，為低速無(wú)載荷軸承故障診斷提供了新的研究方向。