KdV-Burgers-Kuramoto系統的漸近吸引子
張曉明,姜金平,董超雨
KdV-Burgers-Kuramoto系統的漸近吸引子
張曉明,姜金平,董超雨
(延安大學數學與計算機科學學院,陜西延安716000)
研究了KdV-Burgers-Kuramoto方程的漸近吸引子,即利用正交分解法構造一個有限維解序列.首先用數學歸納法證明了該解序列不會遠離方程的整體吸引子,接著證明解序列在長時間后無限趨于方程的整體吸引子,最后給出漸近吸引子的維數估計.
KdV-Burgers-Kuramoto方程;解序列;漸近吸引子;維數估計
1 引言
KdV方程是物理學中非常重要的一類非線性波動方程,已有許多研究[1-3],但對KdV的發展方程,如Benney方程解的研究相對較少,D.J.Benney研究了具有耗散和不穩定因素作用下的KdV方程,文獻[2-4]提出了包含耗散和不穩定效應的一個重要的一維波產生模型Benney方程:
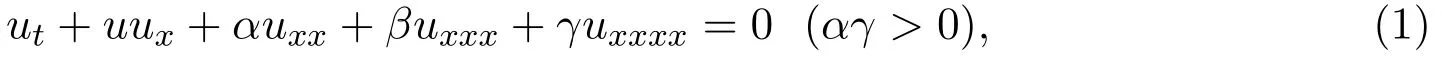
上式稱為KdV-Burgers-Kuramoto方程.當β=1時稱為Kuramoto-Sivashinsky-KdV方程[4],這個方程在等離子體物理、流體動力學和其他領域有著廣泛的應用.
人們在研究無窮維動力系統學性質的過程中,相繼建立了整體吸引子和慣性流形[5-6],將一個無窮維系統約化為一個有限維系統,但是要進一步研究約化后的有限維系統的動力學行為就顯得很困難,因其結構是未知的,所以產生了近似慣性流形、指數吸引子和近似吸引子等概念[6-8],鑒于近似系統與原系統之間缺少較嚴格的等價性,文獻[9]中提出了有限維漸近吸引子的概念.
定義1.1[9]對一個發展系統,其方程為:

記其相空間為H,解算子半群為{S(t),t≥0},吸收集為B.假設對任意u0∈B,存在N維子空間的近似解序列{uk(t),k≥1},滿足:
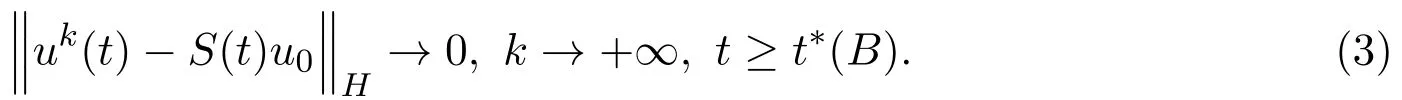
定義

為系統(2)的漸近吸引子,其中∥·∥H為相空間H的模,uk(t)依賴于初值u0,t?(B)只依賴于吸引集半徑,且對B中的u0是一致的.
因為uk(t)為N維系統的解,Ak的結構較易討論,(3)式保證了uk(t)對真解u(t)的漸近逼近性而不僅是近似性.自漸近吸引子提出以來,一些方程的漸近吸引子已經獲得[3,10-12].
本文將討論一維周期邊界條件下的KdV-Burgers-Kuramoto方程:

2 預備知識與解序列的構造
方程(4)-方程(7)的解的存在唯一性證明可參考文獻[13],由此得到相空間([0,2π])和([0,2π])上的解算子半群{S(t),t≥0}.引入類似文獻[14]有關吸收集的結論.
引理2.1對任意初值u0∈([0,2π]),若滿足≤L(<∞),則存在時間
使得

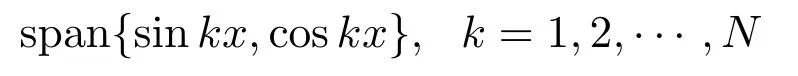
為HN,記([0,2π])到HN的N維正交投影為PN,而QN=I?PN.對

記p=PNu,q=QNu,則u=p+q,用正交投影可將方程分成兩部分:

對任意初值u0(x)∈B,按如下方式構造漸近解序列:

3 逼近性證明
下面考慮漸近解序列uk(x,t)對精確解u(x,t)的逼近性.首先證明,對任意u0∈B,上述序列(11)-序列(12)所得的漸近解序列不會遠離吸收集.
定理3.1設u(x,t)是對應于初值u0∈B的方程(4)-方程(7)的解,qk(k=0,1,2,···)按序列(11)-序列(12)給出,則存在N0∈N和(B),使得當N≥N0時,有

證明由吸收集的正不變性,u0∈B可得u(t)∈B,t≥0,則

為了證明(13)式,只需證明

即可.用歸納法證明,由q0與(11)式作內積得,
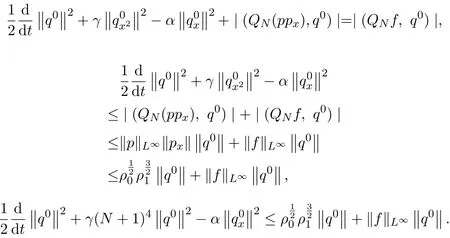
設E(N)=γN4?αN2,則有


即

所以,當N充分大,即滿足

時,有



故由Gronwall不等式,存在

使得

即

當N充分大,滿足
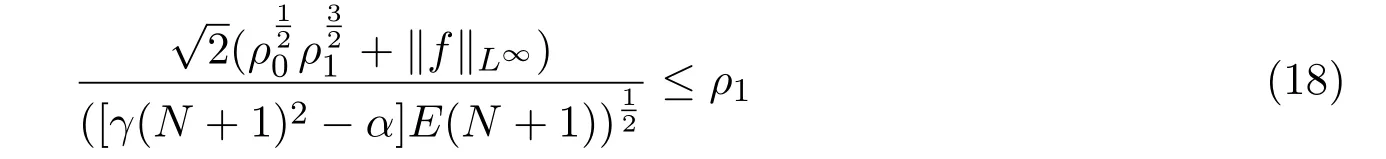
時,有

則由(17)式,(19)式可以說明當k=0時,(15)式成立.現在假設(16)式對k?1成立,即
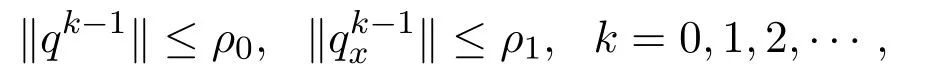
則由(12)式可得,
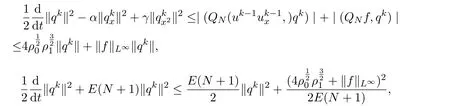
即

由Gronwall不等式知,存在

使得

即

所以,當N充分大時,滿足

時,有


則
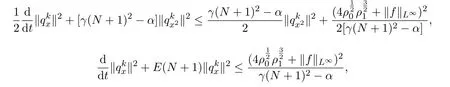
由Gronwall不等式知,存在時間

使得

即

當N充分大,滿足
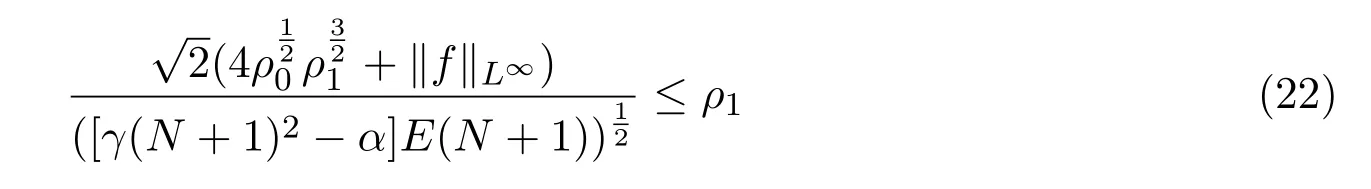
時,有

由(21)式,(23)式可知(15)式對k也成立,由歸納法原理可知,N0取滿足(16)式,(18)式, (20)式,(22)式的最小自然數,=max{,,,},(15)式對一切k∈N成立.
下面證明qk收斂于q.
定理3.2設u(x,t)是對應初值u0的方程(4)-方程(7)的解,qk(k=0,1,2,···).由(11)式-(12)式給出,則存在N1∈N和t?2(B)>0,使得當N≥N1時,有

其中N1為滿足

的最小自然數.
證明記wk=qk?q,由(10)式和(12)式得:
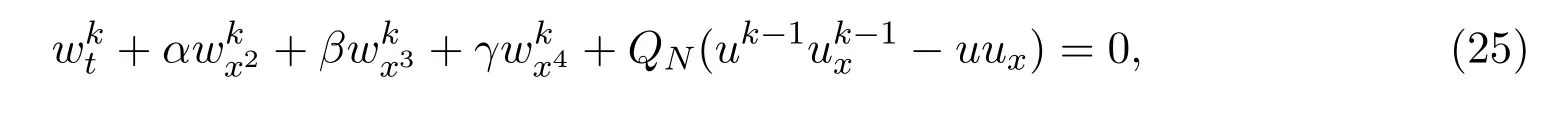
因為
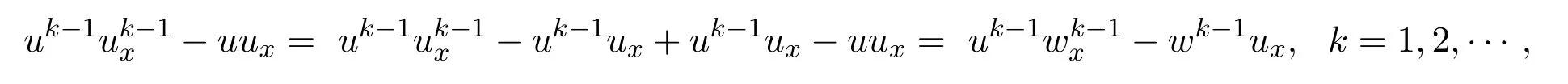
所以由(25)式得:
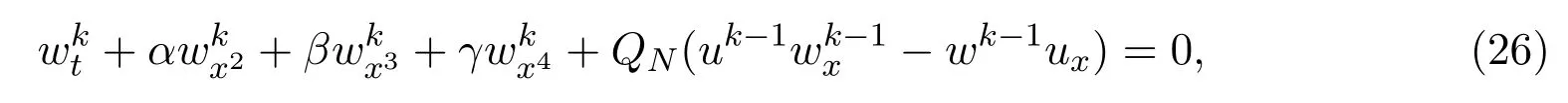


由(10)式和(11)式得:

從而

即




若要使∥wkx∥→0,k→∞,則需要取N1為滿足

的最小自然數.
定理3.3設uk(x,t)為方程(11)-(12)的解,則

為方程(4)-方程(7)的漸近吸引子,且其維數即漸近解序列的維數為滿足條件(20)式,(22)式, (32)式的最小自然數,即

[1]毛杰健,楊健榮.非線性KdV-Burgers-Kuramoto方程新的行波解[J].蘭州理工大學學報:自然科學版, 2006,32(2):150-153.
[2]劉式適,劉式達.物理學中的非線性方程[M].北京:北京大學出版社,2000.
[3]羅宏,蒲志林,馬麗蓉.耗散KDV型方程的漸近吸引子[J].四川大學學報:自然科學版,2009,46(6):1709-1713.
[4]Feng B F,Malomed B A,Kawahara T.Stable periodic waves in coupled Kuramoto-Sivashinsky-Kortewegdevries equations[J].J.Phys.Soc.Japan.,2002,71(11):2700-2707.
[5]Foias C,Sell G R,Temam R.Varites inertills des equations dif f erentielles dissipatives[J].C.R.Acad.Sci. Paris.Ser.I,1985,301:139-142.
[6]Temam R.Inf i nite-Dimensional Dynamical Systems in Mechanics and Physics[M].2nd ed,New York: Springer-Verlag,1997.
[7]Foias C,Manley O,Temam R.Sur linteraction des petits et grands tourbillon’s dans les ecoulements turblents[J].C.R.Acad.Sci.Paris Ser.I,1987,305:497-500.
[8]戴正德,郭柏靈.慣性流形與近似慣性流形[M].北京:科學出版社,2000.
[9]王冠香,劉曾榮.Kuramoto-Sivashinsky方程的漸近吸引子[J].應用數學學報,2000,23(3):329-336.
[10]鄺雪松.四階反應擴散方程的漸近吸引子[J].中山大學學報:自然科學版,2003,42(6):15-18.
[11]趙磊娜.一類非線性發展方程的漸近吸引子[J].重慶大學學報:自然科學版,2007,30(2):136-148.
[12]羅宏,蒲志林.Extended Fisher-Kolmogorov系統的漸近吸引子[J].純粹數學與應用數學,2004,20(2):150-156. [13]馬麗蓉.KdV-Burgers-Kuramoto系統的近似慣性流形[J].四川師范大學學報:自然科學版,2010,33(5):617-620.
[14]王冠香.一維周期邊界條件下Kuramoto-Sivashinsky方程動力學初探[D].蘇州:蘇州大學圖書館,1996.
Asymptotic attractor of KdV-Burgers-Kuramoto equation
Zhang Xiaoming,Jiang Jinping,Dong Chaoyu
(College of Mathematics and Computer Science,Yan′an University,Yan′an716000,China)
In this paper,we study the asymptotic attractor of KdV-Burgers-Kuramoto equations.A solution sequence is constructed by using orthogonal decomposition.It is shown that the solution sequence doesn′t go away from the global attractor in terms of mathematical induction.Then it is obtained that the solution sequence approaches to the global attractor of the equation in long time and the dimensional estimate of the asymptotic attractor is obtained.
KdV-Burgers-Kuramoto equation,solution sequence,asymptotic attractor,dimensional estimate
O175.29
A
1008-5513(2014)06-0595-09
10.3969/j.issn.1008-5513.2014.06.008
2014-04-08.
國家自然科學基金(11171269);陜西省科技計劃項目(2014K150307);延安市科技計劃項目(2013KS03);延安大學研究生教育創新計劃項目.
張曉明(1987-),碩士生,研究方向:無窮維動力系統.
2010 MSC:35B41

