Bezoutian矩陣的一致逼近形式
曹萌
Bezoutian矩陣的一致逼近形式
曹萌
(安徽大學數(shù)學科學學院,安徽合肥230601)
借助閉區(qū)間上的連續(xù)函數(shù)可以用Bernstein多項式一致逼近這一事實,將多項式對所生成的經(jīng)典Bezoutian矩陣和Bernstein Bezoutian矩陣推廣到C[0,1]上函數(shù)對所對應的情形,給出了Bezoutian矩陣一致逼近形式的定義,并且得到如下結(jié)論:給出了經(jīng)典Bezoutian矩陣的Barnett型分解公式和三角分解公式的一致逼近形式;提供了經(jīng)典Bezoutian矩陣和Bernstein Bezoutian矩陣的一致逼近形式的兩類算法;得到了上述兩種矩陣的一致逼近形式中元素間的兩個恒等關(guān)系式.最后,利用數(shù)值實例對恒等關(guān)系式進行驗證,結(jié)果表明兩類算法是有效的.
Bernstein多項式;經(jīng)典Bezoutian矩陣;Bernstein Bezoutian矩陣;一致逼近形式;算法
1 引言
Bezoutian矩陣是一類由兩個多項式所生成的特殊結(jié)構(gòu)方陣,在控制理論、多項式穩(wěn)定性理論等領(lǐng)域中發(fā)揮著重要作用[12],也是矩陣理論的一個熱門研究方向(見文獻[3-9]).另一方面,由于Bernstein多項式自身的優(yōu)良性質(zhì),使得它在計算機輔助幾何設計(CAGD)和計算機圖形學(CG)中具有廣泛的應用[1011].此外,對于由Bernstein多項式所衍生的如Bernstein型算子的研究也受到了科研工作者們的高度重視[1214].
考慮到閉區(qū)間上的連續(xù)函數(shù)可以用Bernstein多項式進行一致逼近這一重要性質(zhì),本文將函數(shù)逼近論思想應用到矩陣理論中來,對多項式對所生成的經(jīng)典Bezoutian矩陣和Bernstein Bezoutian矩陣進行了推廣,給出了C[0,1]上函數(shù)對所生成的Bezoutian矩陣的一致逼近形式的定義.在得出一些自身性質(zhì)的同時,也為豐富和發(fā)展Bezoutian矩陣與友矩陣的纏繞關(guān)系、Bezoutian矩陣經(jīng)Vandermonde矩陣合同后的對角約化以及Bernstein多項式的最大公因式的計算等問題[1517]起著參考作用,具有一定的實際意義.
本文具體安排如下:為了敘述的方便,第二節(jié)首先給出一些需要用到的相關(guān)定義;第三節(jié)給出了經(jīng)典Bezoutian矩陣的Barnett型分解公式和三角分解公式的一致逼近形式;第四節(jié)給出了關(guān)于經(jīng)典Bezoutian矩陣和Bernstein Bezoutian矩陣的一致逼近形式的兩類算法;第五節(jié)得到了經(jīng)典Bezoutian矩陣與Bernstein Bezoutian矩陣的一致逼近形式中元素間的兩個恒等關(guān)系式.在最后一節(jié)中,通過數(shù)值實例對第五節(jié)提供的恒等關(guān)系式進行檢驗,結(jié)果表明所給的兩類算法是有效可行的.
2 預備知識
定義2.1[18]對于給定的多項式對

稱由多項式


所定義的矩陣為p(x)和q(x)在標準冪基{1,x,···,xn?1}下的經(jīng)典Bezoutian矩陣;稱由多項式


下的Bernstein Bezoutian矩陣.這里

定義2.2[19]設f(x)是C[0,1]上的函數(shù),稱

為f(x)的第n個Bernstein多項式.
定義2.3[19]設f(x)是C[0,1]上的函數(shù),如果對于任意的ε>0,存在多項式P(x),使得對于任意x∈[0,1],總有|f(x)?P(x)|<ε成立,則稱f(x)在[0,1]上可以用多項式一致逼近.
3 經(jīng)典Bezoutian矩陣的Barnett型分解公式和三角分解公式的一致逼近形式
引理3.1[19]設f(x)是C[0,1]上的函數(shù),那么?ε>0,?N>0使得n>N時,?x∈[0,1]都有|Bn(f;x)?f(x)|<ε成立,即
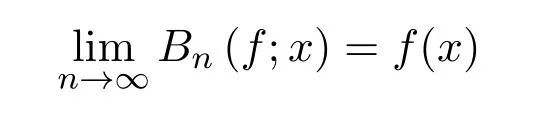
在[0,1]上一致成立.
定義3.1設f(x)和g(x)是C[0,1]上的函數(shù)對,則

和

在[0,1]上一致成立.稱由函數(shù)

所定義的矩陣
為f(x)和g(x)在標準冪基{1,x,···,xn?1}下的經(jīng)典Bezoutian矩陣的一致逼近形式;稱由函數(shù)
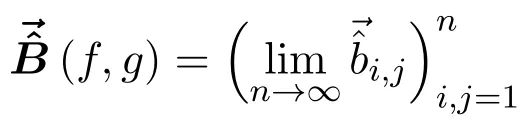

所定義的矩陣

引理3.2[19]

這里?i稱為i階差分算子,?μi=μi+1?μi,i=0,1,···,n?1.
引理3.3[20]對于給定的多項式對


稱為p(x)的對稱化子,

稱為p(x)的第一酉矩陣.
定理3.1設f(x)和g(x)是C[0,1]上的函數(shù)對,則其中

分別稱為C[0,1]上函數(shù)f(x)的對稱化子和第一酉矩陣的一致逼近形式.
證明首先由引理3.2可知

再由定義3.1及引理3.3易知定理3.1成立.
引理3.4[21]對于給定的多項式對


即經(jīng)典Bezoutian矩陣的三角分解公式.
定理3.2設f(x)和g(x)是C[0,1]上的函數(shù)對,則(f,g)

證明首先由引理3.2可知,

再由定義3.1及引理3.4易知定理3.2成立.
4 經(jīng)典Bezoutian矩陣和Bernstein Bezoutian矩陣的一致逼近形式的算法
定理4.1C[0,1]上的函數(shù)對f(x)和g(x)在標準冪基{1,x,···,xn?1}下的經(jīng)典Bezoutian矩陣的一致逼近形式
的算法如下:

證明由題設條件可知,

由引理3.2可知,

從而有

分別比較上式等號兩端xi,xiyj以及xnyj的系數(shù)可知,

即可得出(1)-(3)式,故定理4.1成立.
引理4.1[22]多項式對

在Bernstein基

下的Bernstein Bezoutian矩陣B(p,q)=的算法如下:


定理4.2C[0,1]上的函數(shù)對f(x)和g(x)在Bernstein基

下的Bernstein Bezoutian矩陣的一致逼近形式

的算法如下:

證明根據(jù)引理3.2及引理4.1易知定理4.2成立.
5 經(jīng)典Bezoutian矩陣與Bernstein Bezoutian矩陣的一致逼近形式中元素間的恒等關(guān)系式
引理5.1[22]標準冪基{1,x,···,xn?1}和Bernstein基

之間滿足關(guān)系式:

其中Hn?1=(hi,j)n i,j=1,滿足

定理5.1設C[0,1]上的函數(shù)對f(x)和g(x)在標準冪基{1,x,···,xn?1}和Bernstein基

下的經(jīng)典Bezoutian矩陣和Bernstein Bezoutian矩陣的一致逼近形式分別為

和


證明對于C[0,1]上的函數(shù)對f(x)和g(x),由引理5.1可知,

從而有,




再由(6)式易知,


再由(7)式易知,

即(5)式成立.從而定理5.1成立.
6 數(shù)值實例
例6.1給定C[0,1]上的函數(shù)對f(x)=ex,g(x)=ln(1+x),則稱f(x)和g(x)可分別表示成:

為了方便起見,取i=3,j=1,則由定理4.1可知,

由引理3.2易得,

代入到(8)式中可得,

此外,有

根據(jù)定理4.2可得,

代入到(9)式等號右端,有

從而有

即滿足(4)式,同理可知(5)式成立.
數(shù)值實例表明:定理4.1和定理4.2中的兩類算法是有效可行的,它將定理3.1和定理3.2關(guān)于經(jīng)典Bezoutian矩陣的一致逼近形式的求解具體細化到每一個元素中,為此無需根據(jù)Barnett型分解公式或三角分解公式去求解Bezoutian矩陣的某一特定元素,這將為計算帶來極大的方便.
[1]Fuhrmann P A.A Polynomial Approach to Linear Algebra[M].New York:Springer-Verlag,1996.
[2]Barnett S.Polynomials and Linear Control Systems[M].New York:Springer-Verlag,1983.
[3]Yang Z H.Polynomial Bezoutian matrix with respect to a general basis[J].Linear Algebra and its Applications,2001,331:165-179.
[4]Yang Z H,Hu Y J.A generalized Bezoutian matrix with respect to a polynomial sequence of interpolatory type[J].IEEE Transactions on Automatic Control,2004,49(10):1783-1789.
[5]Wu H Z.Generalized polynomial Bezoutian with respect to a Jacobson chain basis over an arbitrary f i eld[J]. Linear Algebra and its Applications,2010,432(12):3351-3360.
[6]Yang Z H,Cui B F.On the Bezoutian matrix for Chebyshev polynomials[J].Applied Mathematics and Computation,2012,219:1183-1192.
[7]Rost K.Matrix representations of split Bezoutians[J].Linear Algebra and its Applications,2012,436:3904-3918.
[8]Ehrhardt T,Rost K.Resultant matrices and inversion of Bezoutians[J].Linear Algebra and its Applications, 2013,439(3):621-639.
[9]Belhaj S.Computing the polynomial remainder sequence via Bezout matrices[J].Journal of Computational and Applied Mathematics,2013,250:244-255.
[10]盧振泰,陳武凡.基于Bernstein多項式的數(shù)字圖像分存[J].電路與系統(tǒng)學報,2009,14(4):17-20.
[11]嚴蘭蘭.帶形狀參數(shù)的Bernstein-Bezier曲面[J].計算機工程與科學,2014,36(2):317-324.
[12]程麗.Bernstein-Kantorovich算子線性組合同時逼近的正逆定理[J].純粹數(shù)學與應用數(shù)學,2011,27(1):56-62.
[13]單銳,魏金俠,張雁.Bernstein算子矩陣法求高階若奇異積分微分方程數(shù)值解[J].華僑大學學報, 2012,33(5):595-600.
[14]劉國芬.一類推廣的Bernstein-Kantorovich算子的點態(tài)逼近[J].純粹數(shù)學與應用數(shù)學,2014,30(1):32-39.
[15]Fiedler M,Ptak V.Bezoutians and intertwining matrices[J].Linear Algebra and its Applications,1987,86: 43-51.
[16]Chen G N,Yang Z H.Bezoutian representation via Vandermonde matrices[J].Linear Algebra and its Applications,1993,186:37-44.
[17]Winkler J R,Yang N.Resultant matrices and the computation of the degree of an approximate greatest common divisor of two inexact Bernstein basis polynomials[J].Computer Aided Geometric Design, 2013,30:410-429.
[18]Lancaster P,Tismenetsky M.The Theory of Matrices with Applications[M].2nd ed.New York:Springer-Verlag,1985.
[19]常庚哲,史濟懷.數(shù)學分析教程[M].北京:高等教育出版社,2003.
[20]Barnett S.A note on the Bezoutian matrix[J].SIAM Journal on Applied Mathematics,1972,22(1):84-86. [21]Helmke U,Fuhrmann P A.Bezoutians[J].Linear Algebra and its Applications,1989,122-124:1039-1097.
[22]Bini D A,Gemignani L.Bernstein-Bezoutian matrices[J].Theoretical Computer Science,2004,315:319-333.
The uniform approximation form of Bezoutian matrix
Cao Meng
(School of Mathematical Science,Anhui University,Hefei230601,China)
Using the fact that Bernstein polynomial has the character of uniform approximation to continuous function on a closed interval,we generalize the classical Bezoutian matrix and Bernstein Bezoutian matrix generated by a pair of polynomials to functions on the closed interval.The def i nition on the uniform approximation of Bezoutian matrices is given.And we obtain some conclusions about them.Firstly the uniform approximation form of the Barnett type factorization and triangular factorization formulas of classical Bezoutian matrix are presented.Secondly the algorithms of the uniform approximation form with respect to the classical Bezoutian matrix and Bernstein Bezoutian matrix are provided.Furthermore,we obtain two identical relations on elements of the uniform approximation form relative to the two matrices mentioned before.Finally the numerical example is presented to verify the identical relation and show the ef f ectiveness of the algorithms.
Bernstein polynomial,classical Bezoutian matrix,Bernstein Bezoutian matrix,algorithm, uniform approximation form
O151.21
A
1008-5513(2014)06-0649-12
10.3969/j.issn.1008-5513.2014.06.015
2014-07-10.
曹萌(1991-),碩士生,研究方向:矩陣與算子理論.
2010 MSC:15A09

