基于有限元方法的排氣歧管后法蘭疲勞模擬計算
張傲,路明
(安徽江淮汽車股份有限公司技術中心,安徽合肥 230601)
0 引言
某款發動機的排氣歧管后法蘭在兩次全負荷試驗中共斷裂了7次,均是在試驗進行了10~20 h的范圍,全速全負荷試驗發動機轉速為6 000 r/min。經過計算得到后法蘭是在發動機運轉3.6×106~7.2×106次循環后斷裂,初步判斷是由于疲勞引起的破壞。斷裂情況如圖1所示。文中采用有限元分析的方法重現失效模式,并對優化后的模型進行驗證,以便解決斷裂問題。
1 疲勞有限元分析理論
由于各點均為三維應力狀態,故采用復雜應力狀態下的多軸疲勞強度理論計算疲勞安全系數。多軸等效應力幅 (即Mises等效應力幅)為:
式中:σ1a、σ2a、σ3a為局部主應力幅值。
疲勞安全系數為:
式中:σ-1為單軸疲勞極限;Ψσ為平均應力影響系數,一般取0.34,對應的剪切部對稱循環系數Ψτ取0.21;β為表面加工系數,取0.88;ε為尺寸系數,取0.8;σrqm為等效平均應力。
計算等效平均應力一般有3種方法:
(1)Mises等效平均應力法[1]
式中:σ1m、σ2m、σ3m為3個主應力平均值。
(2)Sines平均主應力法[2]
σrqm=σ1m+σ2m+σ3m
(3)應力分量重考慮平均應力方法[3]
計算復雜應力幅分量時將非對稱循環加在對稱循環上去,即:
σx(n)=σxa+Ψσσxm
σy(n)=σya+Ψσσym
σz(n)=σza+Ψσσzm
τxy(n)=τxya+Ψττxym
τyz(n)=τyza+Ψττyzm
τzx(n)=τzxa+Ψττzxm
式中:σxa、σya、σza、τxya、τyza、τzxa分別為各方向上的正應力幅和剪應力幅;σxm、σym、σzm、τxym、τyzm、τzxm分別為各方向上的循環正應力的平均應力和循環剪應力的平均應力。一般情況下,壓平均應力對疲勞損傷無貢獻,因此計算中不考慮負平均應力分量的影響。等效應力幅 (即Mises等效應力幅)為:
疲勞安全系數為:
2 有限元模型
分析模型主要包括排氣歧管、排氣歧管法蘭以及排氣歧管支架等,由于試驗發生斷裂的部位為排氣歧管后法蘭,因此法蘭位置的網格劃分得較密,特別是圓角處,至少劃分4層以上的網格,其他部分可以使用較粗的網格來節省計算時間。分析模型如圖2所示。判斷排氣歧管法蘭主要受到振動載荷,因此疲勞分析工況選取施加6個方向各20g的加速度[4-5],加速度大小的設置主要考慮以下兩個方面的因素:(1)該款發動機為2.0 L排量的發動機,根據爆發壓力的大小推算出外圍附件的加速度一般不超過20g;(2)根據實測的其他位置的加速度情況。結合以上兩個因素,設置載荷為20g加速度。模型中的材料屬性如表1所示。
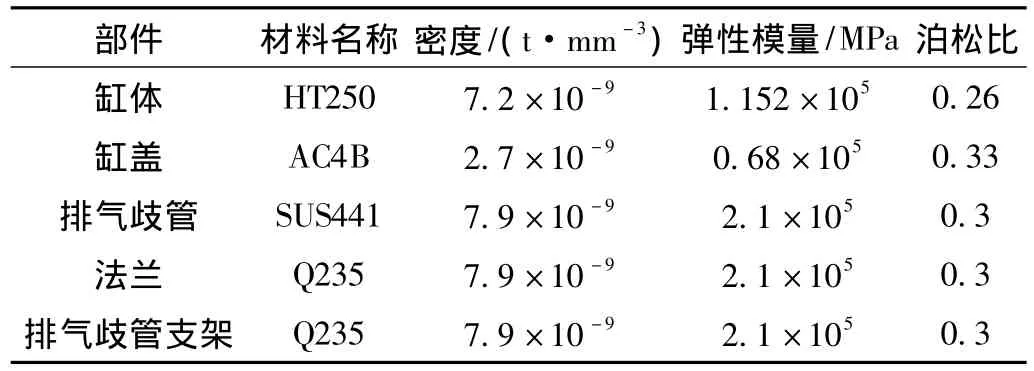
表1 材料關鍵屬性
3 分析結果
6個工況中應力最大的分析結果如圖3所示。可以看出:在施加了20g加速度后排氣歧管后法蘭的最大應力為273 MPa。而利用這6個工況進行疲勞分析后得到的安全系數如圖4所示,可以看出最小安全系數為0.83,小于1.1的限值,位置在法蘭的倒角處,經過觀察后發現:與試驗發生斷裂的位置一致,很好地重現了試驗的故障模式。
由于文中主要計算高周疲勞安全系數,不考慮溫度梯度的影響,而溫度對強度及疲勞參數的影響主要在計算時通過調節材料存活率以及疲勞強度值來實現。并且由于斷裂位置不在焊接部位,分析時也忽略此影響。經過分析后可以發現:斷裂的原因是排氣歧管支架支撐的位置靠近排氣歧管,沒有有效地支撐住排氣歧管法蘭,在較大的振動下發生疲勞斷裂。修改的思路為把排氣歧管支架向后端移動,支撐在法蘭的后端,這樣有效地提升了法蘭圓角位置的剛度。運用同樣的方法對優化后的模型進行分析,應力結果如圖5所示,可以看出:排氣歧管后法蘭的最大應力為80 MPa,比原模型有了很大幅度的提升,安全系數分布如圖6所示,此位置的最小安全系數提升到1.38,大于1.1的限值,滿足要求。
優化后的結構通過400 h全速全負荷試驗后沒有發生斷裂的現象,試驗后的排氣歧管如圖7所示。
4 結論
通過分析,原模型的最小疲勞安全系數為0.83,小于1.1的限值,發生位置與試驗斷裂位置一致。
優化后的模型最小安全系數為1.38,較原模型有了較大的提升,而且經過試驗后未發生斷裂。
通過有限元的方法很好地重現了排氣歧管法蘭的失效模式,并且可以驗證優化后的模型,可以有效地來指導設計,避免斷裂的發生。
【1】徐灝.機械設計手冊:第2卷[M].北京:機械工業出版社,1991.
【2】趙少汴.抗疲勞設計-方法與數據[M].北京:機械工業出版社,1997.
【3】比爾格爾.機械零件強度計算手冊[M].姚兆生,譯.北京:機械工業出版社,1987.
【4】吳道俊,錢立軍,祝安定,等.基于疲勞壽命的車架支架結構優化[J].汽車工程,2013,35(10):863 -867.
【5】朱凌云,路明,胡昌良.發動機附件支架的有限元分析方法研究[J].內燃機,2011,4(2):18-20.

