基于疊加原理的地基極限承載力之誤差分析
房 亮
(上海建筑設計研究院有限公司,上海 200041)
0 引言
淺基礎的極限承載力通常采用Terzaghi的疊加原理形式給出,即分別考慮地基土粘聚力c、基礎底面以上超載q以及土體重度γ對地基承載力的貢獻,然后進行線性疊加求得極限承載力,計算公式為[1]:
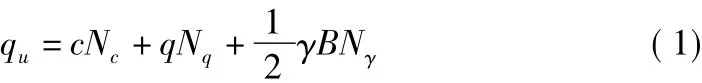
其中,Nc,Nq,Nγ均為地基承載力系數,均為摩擦角 φ 的函數;B為基礎寬度。為了求得地基承載力系數Nc,Nq,Nγ,大多數方法假定兩個不同的破壞機理:一個為考慮超載q但不考慮土體重度γ的c-φ土,另一個為不考慮超載q但考慮土體重度的無粘性土。采用第一個破壞機理可求得Nq,Nc的解析表達式:


采用第二個破壞機理并不能求得Nγ的解析表達式,只能采用數值方法得到其近似數值解。目前常用的數值方法有:極限平衡法[2,3]、極限分析法[4,5]、有限元或有限差分法[6,7]、滑移線法[8,9]。基于Nγ的數值解一些經驗公式被提出以簡化計算。其中比較經典的Nγ公式為:
Terzaghi公式[1]:
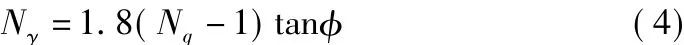
Meyerhof公式[10]:

Hansen 公式[11]:

Vesic 公式[12]:

實際上在極限荷載作用下只有一個破壞模式發生,由于土體材料的非線性,采用傳統的疊加原理計算地基承載力會產生誤差。Michalowski[13]采用極限分析上限法分析地基極限承載力時發現,地基承載力系數不僅依賴于摩擦角,還與無量綱參數c/(γB)和 q/(γB)有關。Smith[14]采用滑移線法分析發現,疊加原理引起的誤差最高可達25%,因此承載力計算的疊加誤差應該予以考慮。同時基于不同的假定采用不同的數值方法求解地基承載力系數Nγ也會引入誤差。由于基于疊加原理的極限承載力公式及以上四個Nγ的經典公式被廣泛應用,分析采用這些公式時的誤差具有重要的工程意義。近期的研究成果發現,如果假定土體為理想彈塑性材料,由滑移線法得到的極限地基承載力為精確解[14],故本文采用 Martin[15]基于滑移線法的軟件 ABC計算地基極限承載力并與經驗公式求得的結果進行比較,該軟件在各種極端條件下均能高精度的求得地基極限承載力。
1 地基承載力問題的等效處理[16]
淺基礎的極限承載力是c,φ,γ,B與q的函數,針對每一組(c,φ,γ,B,q)都可單獨求出一個極限承載力,為了系統的進行誤差分析需要對地基承載力問題進行等效處理。假定土體為理想剛塑性材料,根據摩爾—庫侖破壞準則得:

其中,σ1,σ3分別為最大和最小主應力。式(8)可被寫成下式形式:

式(9)表明一般的c-φ土可以看作為在土體處增加一個c cotφ壓力的無粘性土。
如圖1a)所示,基于疊加原理的地基極限承載力為:
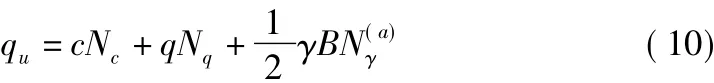
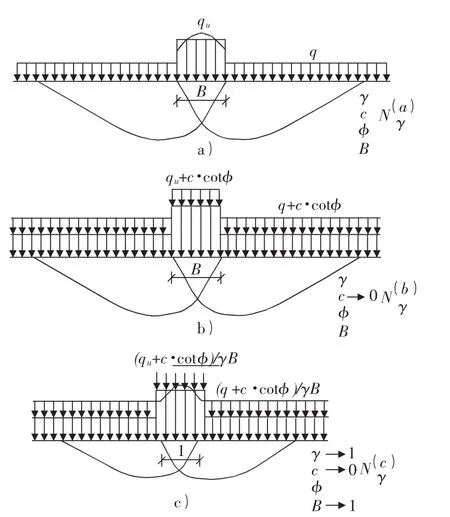
圖1 地基承載力的等效處理
然后將土體看作無粘性土,同時在地表及基礎上施加正應力c cotφ,如圖1b)所示,則極限承載力可表示為:
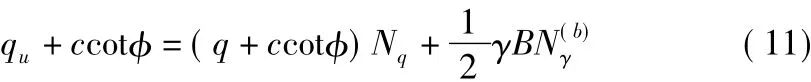
式(11)左右同時除以γB則可得到無量綱化的極限承載力公式,如圖1c)所示:
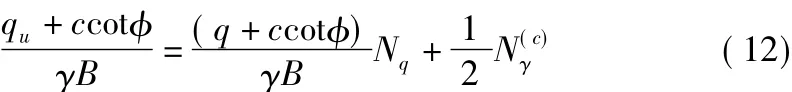
通過比較式(10)~式(12)可知:


Pu為無量綱化的極限承載力,λ為無量綱化的超載。從而地基承載力問題可以簡化為下面的問題進行分析:土體重度γ=1,基礎寬度B=1,超載q=λ,土粘聚力c=0。
2 誤差分析
針對特定的λ值,將式(4)~式(7)中任一個Nγ經驗公式代入式(14),均可得到無量綱的地基極限承載力。由于這四個經典的經驗公式并不是精確的表達式,因此會引入誤差。其誤差可采用下式進行評估:

其中,Pu為準確的無量綱極限承載力,可采用ABC軟件直接求出;Ncγlassical為式(4)~式(7)中任一個Nγ經驗公式;v為誤差因子,當v>1時表明采用經驗公式求得的極限承載力小于準確值,當v<1時表明采用經驗公式求得的極限承載力大于準確值。
圖2a)為采用Terzaghi經驗公式時的誤差分析,由圖可知,當摩擦角φ=5°時,v隨著λ的增大從1.28先增大到1.41然后減小到1,在整個過程中v均不小于1,表明φ=5°時采用Terzaghi經驗公式求得的極限承載力小于準確值。當摩擦角φ=20°時,v隨著λ的增大從0.8先增大到1.14然后減小到1,表明φ=20°時,當λ<0.6采用Terzaghi經驗公式求得的極限承載力大于準確值;當λ>0.6采用Terzaghi經驗公式求得的極限承載力小于準確值。當摩擦角φ=35°時,v隨著λ增大的變化規律與φ=20°時類似,經驗公式求得的極限承載力先大于準確值然后小于準確值。當摩擦角φ=50°時,采用Terzaghi經驗公式求得的極限承載力均小于準確值。
圖2b)為采用Meyerhof經驗公式時的誤差分析,由圖可知,當摩擦角φ=5°時,v隨著λ的增大從1.63先增大到1.70然后減小到1,在整個過程中v均不小于1,表明φ=5°時采用Meyerhof經驗公式求得的極限承載力均小于準確值。當摩擦角φ=20°時,v隨著λ的增大從0.99先增大到1.23然后減小到1,表明φ=20°時,經驗公式求得的極限承載力先大于準確值然后小于準確值。當摩擦角φ=35°與φ=50°時v隨著λ增大的變化規律與φ=20°時類似,經驗公式求得的極限承載力先大于準確值然后小于準確值。
圖2c)為采用Hansen經驗公式時的誤差分析。通過比較式(4)和式(6)可知Hansen經驗公式與Terzaghi經驗公式類似,因此圖2c)中v隨著λ的增大的變化規律與圖2a)相似。當φ=20°且λ<0.005時v略小于1,其余情況下v均大于1。因此采用Hansen經驗公式時經驗公式求得的極限承載力基本上均小于準確值,偏安全。
圖2d)為采用Vesic經驗公式時的誤差分析,由圖可知,當摩擦角φ=5°時,v隨著λ的增大而增大最終趨于1,在整個過程中v均不大于1,表明φ=5°時采用Vesic經驗公式求得的極限承載力均大于準確值。當摩擦角φ=50°時v隨著λ增大先增大后減小,經驗公式求得的極限承載力先大于準確值然后小于準確值。通過圖2d)可知,大多數情況下v均小于1,因此采用Vesic經驗公式時經驗公式求得的極限承載力基本上大于準確值,偏不安全。
3 結語
1)由于土體的非線性及計算模型不準確,常用的一些經典公式均存在著誤差。經驗公式求得的極限承載力可能大于準確值也可能小于準確值。
2)采用Hansen經驗公式求得的極限承載力基本上小于準確值,偏安全,當現場得到土體的摩擦角較準確時,可采用Hansen公式計算地基極限承載力從而得到偏保守的值。
3)采用Vesic經驗公式求得的極限承載力基本上大于準確值,偏不安全。當現場試驗得到極限承載力時,可采用Vesic公式反分析求得土體摩擦角。采用反分析得到的摩擦角對附近類似工程進行極限承載力分析時可以得到偏保守的結果。
[1]Terzaghi K.Theoretical soil mechanics.New York,John Wiley& Sons,1944.
[2]Meyerhof G.G.The ultimate bearing capacity of foundations[J].Géotechnique,1951,2(4):301-332.
[3]Zhu D.Y,Lee C.F,Jiang H.D.A numerical study of the bearing capacity factor Nγ[J].Can.Geotech.J,2001,38(5):1090-1096.
[4]Kumar J.Effect of footing-soil interface friction on bearing capacity factor Nγ[J].Géotechnique,2004,54(10):677-680.
[5]Hjiaj M,Lyamin A.V.,Sloan S.W..Numerical limit analysis solutions for the bearing capacity factor Nγ[J].Int.J Solids Struct,2005,42(5-6):1681-1704.
[6]Frydman S.,Burd H.J..Numerical studies of bearing-capacity factor Nγ[J].J.Geotech.Geoenviron.Engng,ASCE,1997,123(1):20-29.
[7]Loukidis D.,Salgado R..Bearing capacity of strip and circular footings in sand using finite elements[J].Comput Geotech,2009,36(5):871-879.
[8]Bolton M.D.,Lau C.K..Vertical bearing capacity factors for circular and strip footings on Mohr-Coulomb soil[J].Can.Geotech J,1993,30(6):1024-1033.
[9]Kumar J.Nγ for rough strip footing using the method of characteristics[J].Can.Geotech.J,2003,40(3):669-674.
[10]Meyerhof G.G.Some recent research on the bearing capacity of foundations[J].Can.Geotech.J.,1963(1):16-31.
[11]Hansen J.B..A revised and extended formula for bearing capacity[J].Danish Geotechnical Institute,Copenhagen,Bulletin,1970(28):5-11.
[12]Vesic A.S..Analysis of ultimate loads of shallow foundations.Journal of the Soil Mechanics Foundations Division.ASCE,1973,99(1):45-73.
[13]Michalowski R.L..An estimate of the influence of soil weight on bearing capacity using limit analysis[J].Soils and Foundations,1997,37(4):57-64.
[14]Smith C.C..Complete limiting stress solutions for the bearing capacity of strip footings on a Mohr-Coulomb soil[J].Géotechnique,2005,55(8):607-612.
[15]Martin C.M..ABC-Analysis of bearing capacity.Available online from www-civil.eng.ox.ac.uk/people/cmm/software/abc/,2004.
[16]Zhu D.Y.,Lee C.F.,Law K.T..Determination of bearing capacity of shallow foundations without using superposition approximation[J].Can.Geotech.J,2003,40(2):450-459.

