冶金企業內部鐵路網絡區域劃分研究

陳建強，張 昱，李春明

（1. 中鐵第四勘察設計院集團有限公司 通號處， 武漢 430063；2. 鐵道第三勘察設計院集團有限公司，天津 300142；3. 中鐵第五勘察設計院集團有限公司，北京 102600）

冶金企業內部鐵路網絡區域劃分研究

陳建強1，張 昱2，李春明3

（1. 中鐵第四勘察設計院集團有限公司 通號處， 武漢 430063；2. 鐵道第三勘察設計院集團有限公司，天津 300142；3. 中鐵第五勘察設計院集團有限公司，北京 102600）

針對冶金企業內部的鐵路線路呈網狀分布的特點，提出一種基于共鄰點矩陣與復合度函數、綜合考慮劃分子區域所需列車控制防護能力的線路網區域劃分方法，并應用該劃分方法對某鋼廠企業的鐵路線路網進行了區域劃分，該劃分結果有效地指導了區域控制系統控制范圍的設計與規劃。

冶金企業；內部鐵路線路網；區域劃分；共鄰點矩陣；復合度函數；區域控制能力

鐵路運輸是冶金企業生產的動脈，列車運行控制系統是鐵路運輸的神經中樞，區域安全控制系統（RSCS ，Regional Security Control System）作為列控系統的核心部分，是實現列車安全高效運行最終執行者。在冶金企業內部，為了滿足企業內部物料運輸準時性要求，列車的接發車作業和機車的取送作業等交叉同時進行，整體鐵路運輸十分繁忙[1]，若整個廠區鐵路運輸只設置單個RSCS，則其所要控制的列車數將以百計，同時需要處理的數據量十分龐大，邏輯關系極為復雜，考慮到被自動控制的列車的登錄或注銷需盡快被響應，從而及時獲得行車憑證以確認其安全的運行，最終完成相應的運輸任務，因此單個系統難以做到。另外，一旦單個系統發生故障，將導致整個鐵路運輸系統降級進入人工控制模式，極大地降低運輸效率，所以應對冶金企業內部的整個鐵路網絡進行劃分，由多個系統分別控制。而合理的重疊劃分還可對重疊區域實現冗余控制，當重疊區的某個控制子系統發生故障時，可以由該重疊區上的其他子系統控制，進而提高了重疊區安全防護的可靠性。綜上所述，合理安排每個RSCS的控制范圍，以實現其控制能力的最大化并獲得最佳的控制效果，對于實現冶金企業內部鐵路運輸的自動化控制具有十分重要的意義[2]。

由于冶金企業內部的鐵路線具有網狀分布的特點，若以冶金企業內部各個生產車間內的各個停車點、煉鐵高爐區各個高爐停車位、各個廠內功能編組站和聯合編組站為頂點，各個頂點之間的鐵路線為連線邊構建網絡模型[3]，由于各個頂點之間可能同時存在多條鐵路線相連線路，線路網各個頂點之間的單條連線就具有了權重，且可雙向行車，因此線路網是一個無向有權的網絡。所以，合理安排每個RSCS的控制范圍問題就成了如何對此線路網進行區域劃分的問題。

對于復雜網絡區域劃分的相關研究大體包含計算科學中的圖形分割[4～5]和社會科學中的層次聚類[6～8]，以及由Donetti和Newman等人提出結合二者優缺點，引入一種衡量頂點間的相似性標準模塊度的結合譜分析和凝聚算法特點的算法[10～12]，并推廣到加權網絡中。文獻[13]、[14]受模塊度思想的啟發，以頂點與頂點之間所擁有的共鄰點數作為區域劃分的衡量標準，由此將基于共鄰點矩陣和復合度函數的算法推廣到加權網絡中，結果明顯優于Newman等人基于模塊度的多區域劃分算法和其他的區域劃分算法。因此，參考文獻[14]，本文定義一個共鄰點矩陣和一個復合度函數，綜合考慮劃分子區域所需列車控制防護能力，提出一種針對企業內部的鐵路網絡進行區域劃分方法，最后利用這種劃分方法對某大型鋼廠鐵路網進行區域劃分，分析劃分結果的有效性并據此劃分結果設計RSCS的控制區域范圍，控制結果表明所述劃分方法有效可行。

1 基于共鄰點矩陣與復合度函數的線路網區域劃分算法

區域劃分問題可描述為一個并行計算的問題：假設有n個來自各個頂點的運輸任務需由x個RSCS完成，每個任務不一定和其他任務有直接關聯。所有的運輸任務之間的關聯模式由整個廠內的鐵路網來表示，如圖1所示，網絡中每一個頂點對應一個運輸任務，而每條邊就連接了一對需要直接聯絡的關系。區域劃分的問題就是如何分配這n個頂點（包含運輸任務）到這x個RSCS上，使得每個RSCS處理的運輸任務數近似相等，且各個RSCS之間連接的邊數最少，從而使各個RSCS之間的通信量最小（也就是發生區域交接的次數最少，因為區域交接會在某種程度上影響運輸效率）。

當企業內部的鐵路網絡的規模很大時，找到一個使各個區域安全控制系統之間連接的邊數最少，從而使各個區域安全控制系統之間的通信量最小的區域劃分問題的精確解是一個NP難問題，因此本文采用試探性算法以期求得滿意解。

1.1 帶有權重的聯結矩陣及其共鄰點矩陣

為便于描述，將上述線路網G抽象為一個由頂點集V(G)={1, 2,…, i,}和邊E(G)={(i1, j1), (i2, j2), …}組成的圖，若(i, j)=(j, i)，則G為無向圖，否則為有向圖[15]。若定義：

圖1 具有區域結構的企業內部鐵路線路網絡示意圖

則聯結矩陣A={aij}表示圖G中頂點之間的連接關系，由于上節所構建的線路網是一個無向有權的網絡，因此 是一個非零元素代表邊的權重的對稱的0-1矩陣[13～14]，也就是把頂點之間有n條邊相連看作是權重為 的1條邊聯結著2個頂點，如圖2（b）所示為某簡易加權線路網的示意。若定義共鄰點矩陣 H，則其各個元素可表示為[14]：

由于只有當第i個頂點和第j個頂點有邊相連時，aikakj=1，因此Hij表示頂點i和頂點j共有相同鄰點的數目。如圖2（a）中，頂點IV就是頂點I與頂點II的一個共鄰點，其共鄰點矩陣H的計算如圖2（b）所示。

圖2 簡易區域內網絡及其共鄰點矩陣

而圖2（c）中，由于頂點I通過頂點IV到達頂點II的路徑有6條，因此可以認為頂點I與頂點II擁有共鄰點（即頂點IV）的數量為6，其共鄰點矩陣H的計算如圖2（d）所示，其中非零元素代表邊的權重。

1.2 復合度函數

由于基于共鄰點矩陣區域劃分的算法是通過使區域內部的頂點對之間擁有盡可能多的共鄰點，因此需要定義一個復合度函數，以度量共鄰點的多少，繼而通過尋找一種區域劃分使復合度函數最大，獲得算法搜索的終止條件。結合公式（1）和公式（2），參照文獻[11～12]中對隨機相連的網絡中兩個頂點有邊相連的概率表示，以di和dj分別表示頂點i和j的度，didj/n表示當網絡隨機相連接時頂點對之間擁有的共鄰點的數目，復合度函數的定義如下：

其中∏ij表示頂點i和j的區域認定函數，且

可見，Ψ體現了區域內部頂點對之間擁有的共鄰點的數目與在隨機網絡相連的情況下的數目的差，也就是當Ψ＜0時，網絡中將不存在區域結構。

1.3 基于共鄰點矩陣和復合度函數的線路網的區域劃分算法

首先定義一個標示向量Θ，其各個元素為：

則有：

因此，復合度函數為：

若定義對稱矩陣X為復合度矩陣：

則可將式（8）寫成：

由于X為實對稱矩陣，當n個特征值互異時，利用其標準正交基η1, η2,…,ηn表示向量X，有寫成δi=ηT

iX代入式（10），可得到：

其中：ζi指X對應的特征向量ηi的特征值。

若假設ζ1≥ζ2≥…≥ζn，通過選擇適當的δi使式（11）中的最大特征值的那一項在最大化Ψ'時發揮主要作用。在一般的譜分析中，若標示向量?的選取無約束，則可選其正比于矩陣X的主特征向量η1（表示最大特征值對應的特征向量），而式（5）中對?具有限定，因此?不能平行于η1，故只能選擇?盡可能平行于η1，獲得較好的次優解，也就是令：

其中，ηi1表示主特征向量η1中的第i個元素。

上述過程可以總結為：首先求得復合度函數最大特征值的主特征向量，然后根據主特征向量中的元素符號把網絡劃分為兩個區域。若復合度函數的最大特增方程為m重根，需要對其對應的m 個特征向量Schmidt正交化，然后根據m個正交化后的特征向量中的元素符號把網絡劃分為兩個區域，共有m種不同的結果。

至此，上述方法可將線路網劃分為兩個區域，然而這往往是不夠的。為了繼續進行劃分，可以先假設其中一個區域為ξ，且該區域包含nξ個頂點，將上述劃分方法繼續用在區域ξ，繼續將其劃分為更小的區域。但是當一個網絡被劃分為兩個區域之時，由于已刪去了連接這兩個區域的邊，導致區域內部頂點的度發生了變化。為此，這里給出繼續劃分子區域ξ的過程中產生的復合度函數ψ的增量?Ψ計算公式：

其中：

重新定義針對區域 中頂點的復合度矩陣：

從而式（15）可以寫成：

由于式（16）與式（10）的形式相同，因而可與上述劃分兩個區域時使Ψ最大化的方法使?Ψ最大化來劃分區域ξ。文獻[13]根據復合度函數Ψ是否繼續增加作為是否終止劃分的條件，即當?Ψ≤0（說明整個網絡經過劃分后各個子區域已經不再存在區域結構特征）時，終止劃分。但對于本文，如果只是參考上述終止條件將使劃分的區域范圍過小，造成RSCS控制能力的浪費，進而抬高了造價與成本。同時由于重根的存在，上述劃分方法可能得出多種劃分方案，本質上，這些劃分結果只是考慮了區域之間交接最少的目標，而未考慮RSCS控制能力的利用。因此，下文將參考系統設計的相關知識，結合實際，給出另一個綜合考慮RSCS控制能力區域劃分的終止條件。

1.4 各個控制系統的控制能力的計算及其能力邊界

在冶金企業內部的線路網的相關運輸中，各個頂點之間因為運輸需求的存在而聯結在一起，這些運輸關系包括接發車和取送車作業，前者主要對應于鐵路局列車的運輸作業，后者則主要是廠內的生產運輸。由于企業內部的連續不間斷生產的特點，在一定的周期內，各個生產車間對所需物資的運輸需求相對穩定，因此其鐵路線路網上各個頂點之間所運輸的物資種類和運量相對比較固定，這使得對各個頂點的運輸需求的確定提供給了可能，因而可以確定出各個頂點之間運輸的繁忙程度，進一步確定子區域所需的RSCS控制能力。考慮到所設計的RSCS的控制能力一般考慮單個系統同時能處理的可能同時存在：

（1）已設置的路徑數R；（2）已激活的TSLA（臨時限速服務區域）個數TSLA；（3）已激活的緊急區域個數EB；（4）控制的道岔組的范圍l道岔；（5）需要裝或卸的裝卸區個數FH；（6）登錄的列車數量V。

計算所劃分的子區域所包含的上述R、TSLA、EB、l道岔、FH和V的值，由于在特殊情況下，如果發生區間列車堵塞現象，這時列車運行速度已經下降，當RSCS控制的列車數量超過RSCS容量時，新列車將無法呼叫RSCS以取得行車憑證正常運行，因此，對于上述各個數目的值應設定一定的冗余量?，各個冗余值?FH和?V根據各個區域的線路特點和生產設備商所提供的RSCS設備性能進一步確定，本文分別取表1中的值。

表1 各個參量的冗余值

故所劃分的子區域需滿足式（17）成立：

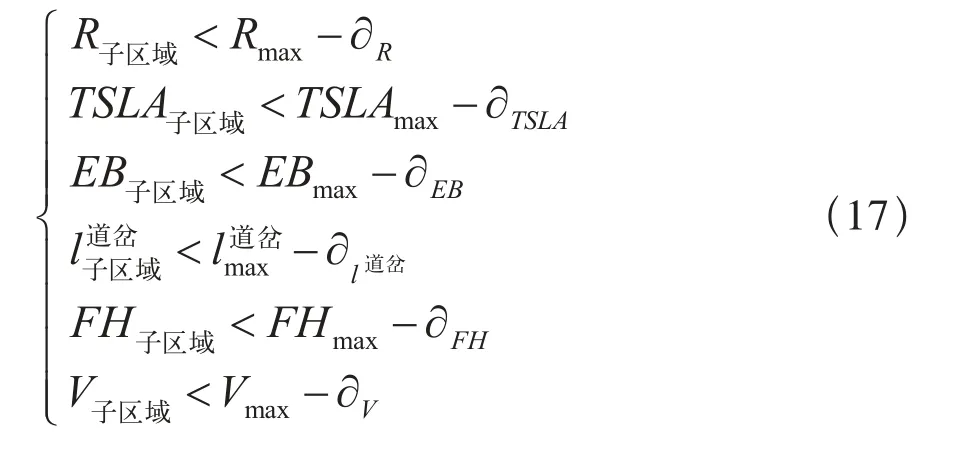
其中：下標為“子區域”分別表示劃分所得的子區域所包含的R、TSLA、EB、l道岔、FH和V的值，下標為“max”表示單個RSCS所能監控的 R、TSLA、EB、l道岔、FH和V的最大值，該值由設備生產商提供。式（17）即為RSCS的控制能力邊界。R、TSLA、EB、l道岔、FH和V值的計算方法如下：

（1）對于R，由于取消了軌道電路，不存在嚴格的路徑概念，因此計算路徑R的數量以所劃分的子區域內所可能完成的運輸任務所需要安排的路徑的最大值，這個值可通過機車車輛控制中心獲得，其根據調度任務綜合計算求得；

（2）對于TSLA，根據整個企業生產廠區的全局地圖上的鐵路線路數據，當子區域劃分出來后，只需在相應的范圍內搜索即可獲得；

（3）對于EB和FH的計算方法同（2）；

（4）對于l道岔，根據整個企業生產廠區的全局地圖上的鐵路線路數據，確認所劃分的子區域最大范圍不超過設定范圍；

（5）對于V，包括區間列車數量V區間、站內停車數量V站內以及RSCS控制分界口列車數量V分界口，即：

其各部分求解方法如下。

a.區間列車數量V區間

由于冶金企業內部的鐵路運輸基本都是貨物運輸，且運送不同貨物的列車具有不同的等級，在同一區間上采用的運行速度也不盡相同，因此其運行圖呈現非平行的特點，參考文獻[16]，將冶金企業內部各種類型的列車定義成3個不同等級，并定義其相應的扣除系數（即在運行圖上鋪畫列車時需要從平行運行圖上扣除的列車對數或列數），某鋼廠采用的扣除系數如表2所示[17]：

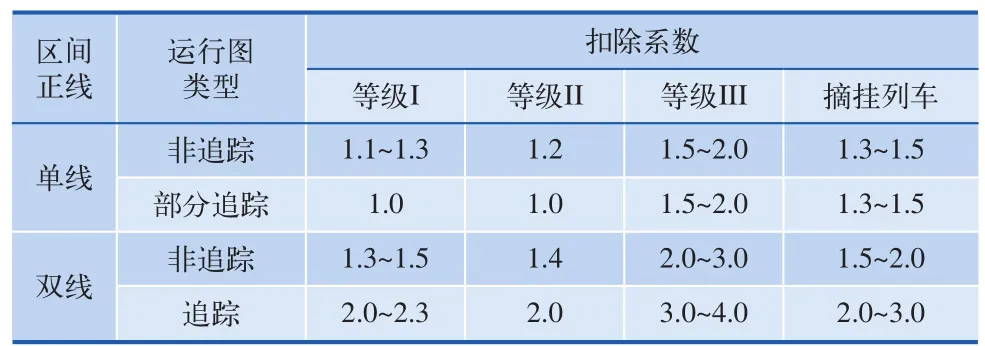
表2 扣除系數表

非平行運行圖的通過能力η非的計算公式為[16]：

其中：K指一個T周中所包含的列車對數或列數，T周指平行運行圖上任何一個區段的列車運行線以同樣的鋪畫方式所排列的一組列車占用區間的時間，詳見參考文獻[16]，這里不再贅述；εI～εIII分別指等級為I～III的列車扣除系數；ε摘掛指摘掛列車扣除系數； nI～nIII分別代表鋪畫在非平行運行圖上的等級為I～III的列車對數或列數； n摘掛代表鋪畫在非平行運行圖上的摘掛列車對數或列數。

根據式（19）和表2的扣除系數，結合企業內部已有的鐵路運輸運行圖，可求得區間列車數量：

b.車站停車數量V站內

在計算區間列車數量V區間時，實際已經考慮了車站正線股道上的列車，因此在計算車站停車數量V站內時，只需要計算到發線的停車數，即待發列車數和調度列車數，這兩個數可分別由到發線股道數（每股到發線為1列）和車站的編組能力（一般每3條調車線有1輛摘掛機車作業）取其總和的最大值求得。

c.分界口列車數量V分界口

冶金企業內RSCS的區間管轄范圍內與外部一般有多處分界口，若n個接口處為雙線則取2列，m個接口處為單線取1列，共有車數2n+m列。

1.5 區域劃分算法

綜上，對于冶金企業內部鐵路線路網區域劃分的最終算法如下：

步驟1：對冶金企業內部的鐵路線路網G中的頂點進行相應的編號，求解G的復合度矩陣ΨG；

步驟2：求解復合度矩陣ΨG的最大特征值，若最大特征值不存在重根，轉步驟4；

步驟3：若最大特征值存在m重根，依次取其中一個重根，轉步驟4，并存儲每一種劃分結果；

步驟4：根據Lanczos方法求解最大特征值所對應的主特征向量，根據主特征向量的元素符號把鐵路線路網劃分為兩個區域；

步驟5：根據上述方法及公式計算所有劃分結果中每個子區域的R、TSLA、EB、l道岔、FH和V的值，判定式（17）是否滿足，若滿足，則終止劃分，比較各個劃分結果，選取各個R、TSLA、EB、l道岔、FH和V的值最為接近的一組為最終解，否則繼續下一步；

步驟6：對于每一個子區域，用式（16）來代替式（10），重復步驟2；

步驟7：斷定Ψ是否繼續增加，即若?Ψ≤0成立，則終止劃分，否則轉到步驟2。

由于線路網具有較明顯的區域特征，對于頂點數為n，邊數為m的網絡，步驟2中線路網的復合度矩陣是一個稀疏矩陣，其主特征值λ2能很快從其他特征值中分離出來，因此步驟4中用Lanczos方法計算其主特征向量的時間復雜度約為m/(λ3–λ2)；而步驟5計算過程的時間復雜度為m+n，因此整體算法時間復雜度約為O(n(n+m))。

2 應用示例

本文根據上述劃分方法，對某鋼廠企業內部的鐵路線路網進行區域劃分，并將自主研制的針對企業內部鐵路運輸區域控制系統軟件在自主構建的冶金企業仿真環境中布置安排，通過其運行結果來驗證本文所提劃分方法的有效性。圖3為某實際鋼廠的鐵路運輸情況。

圖3 某鋼廠的鐵路運輸狀況

其內部共有原料站1個，中心庫1個，機務段2個，熱電站2個，連鑄連軋廠3個，線材廠2個，中板廠2個，煉鋼廠4個，煉鐵廠3個，軋鋼廠4個，工廠站4個，綜合料場2個，渣池3個，綜合利用加工廠1個，酸洗鍍鋅廠1個，鍋爐房2個，高爐5個，原料房2個，焦化站1個，焦化廠3個，燒結廠3個，其相應的路徑數R為513條，TSR（臨時限速服務器）個數為126個，緊急區域個數EB為234，道岔組的范圍l道岔為21 km以內，裝卸區個數FH為147個，車數量V為287列。上述鐵路線路網的區域劃分結果如圖4所示。

圖4 某鋼廠的鐵路線路網區域劃分結果

圖4 中，3次劃分把整個線路網劃分為4個區域：

區域1中：R=123條；TSR =34個；EB =67個；l道岔＜12 km；FH=36個；V=94列。

區域2中：R=166條；TSR =46個；EB =76個；l道岔＜14 km；FH=56個；V=57列。

區域3中：R=94條；TSR=19個；EB=43個；l道岔＜9 km；FH=23個；FH=63列。

區域4中：R=130條；TSR=27個；EB =48個；l道岔＜16 km；FH=32個；V=73列。

根據該劃分結果設計布置區域控制系統的控制范圍，應用結果不僅實現了交接區域路徑最少，交界區的切換次數最少（相鄰區域監控系統之間的交換數據量最少），簡化區域交接過程的復雜性，提高了安全可靠度，同時滿足每個RSCS的控制范圍在其能力之內，且不至于太小（當小于其控制范圍內的列車在舒適運行狀態下的常用制動距離時，將導致相鄰兩個區域監控系統跨區呼喚而引起控制權的競爭，最終導致諸如“幽靈列車”出現等故障的發生，引發危險事故），各個RSCS的控制能力合理分布。

3 結束語

本文針對冶金企業內部的鐵路線路呈網狀分布的特點，構建線路網絡模型，參考復雜網絡劃分的相關理論，提出一種基于共鄰點矩陣與復合度函數、綜合考慮劃分子區域所需列車控制防護能力的線路網區域劃分方法，并應用該劃分方法對某鋼廠企業的鐵路線路網進行了區域劃分，根據該劃分結果設計布置區域控制系統的控制范圍。應用結果表明，本文所提出的劃分方法能有效地指導區域控制系統對列車控制范圍的設計與規劃，對于有效防護列車的安全運行，實現鐵路運輸的自動化具有實際指導意義。

[1] 李鵬云，牛清梅，崔新金，等．淺談冶金企業鐵路運輸的發展[J]．安陽師范學院學報，2003（2）：87-89.

[2] 苑志斌，安海軒，魏啟寧.2013-2017年中國冶金工業投資分析及前景預測報告[J] .中投顧問，2013（8）：1-7.

[3] 何 誠.中國鐵路網的復雜網絡性質研究[D].廣州：中山大學，2007：38-60.

[4] Garey M R, Johnson D S. Computers and Intractability:A Guide to the Theory of NP-Completeness[M]. San Francisco: Freeman Publishers, 1979.

[5] Kernighan B W, Lin S. An efficient heuristic procedure for portioning graphs[J]. Bell System Technical Journal, 1970（49）：291-307.

[6] Scott J. Social Network Analysis: A Handbook[M]. Sage Publications, London, 2000.

[7] Fiedler M. Algebraic connectivity of graphs[J]. Czechoslovak Mathematical Journal, 1973, 23 (98): 298-305.

[8] Pothen A, Simon H, Liou K P. Partitioning sparse matrices with eigenvectors of graphs[J].SIAM Journal on Matrix Analysis and Applications. 1990, 11(3): 430-452.

[9] Girvan M, Newman M E J. Community structure in social and biological networks[J]. PNAS, 2001, 99(12): 7821-7826.

[10] Donetti L,Munoz M A. Detecting network communities: A new systematic and efficient algorithm[J]. Stat. Mech. Thior. Exp, 2004(10): P10012.

[11] Newman M E J. Analysis of weighted networks[J]. Phys. Rev. E, 2004, 70(5): 056131.

[12] Newman M E J. Finding community structure in networks using the eigenvectors of matrices[J]. Physical Review. E, 2006, 74(3): 036104.

[13] 郭崇慧，張 娜.基于共鄰矩陣的復雜網絡社區結構劃分方法[J].系統工程理論與實踐，2010，30（6）： 1077-1084.

[14] 張 娜.復雜網絡社區結構劃分算法研究[D]. 大連：大連理工大學，2009：13-24.

[15] 汪小帆，李 翔，陳關榮.復雜網絡理論及其應用[M].北京：清華大學出版社，2006：17-25，46-54.

[16] 高繼祥.鐵路信號運行基礎[M]. 北京：中國鐵道出版社，2008：80-84.

[17] 賈忠孝.廠礦鐵路運輸組織[M]. 北京：冶金工業出版社，1994：107-112.

責任編輯 方 圓

Regional division of railway network for metallurgical enterprises

CHEN Jianqiang1, ZHANG Yu2, LI Chunming3
( 1. Communication & Signal Design & Research Dept., China Railway Siyuan Survey and Design Group Co., LTD., Wuhan 430063, China; 2. The Third Railway Survey and Design Institute Group Corporation, Tianjin 300142, China; 3. China Railway Fifth Survey and Design Institute Group Co., LTD., Beijing 102600, China )

metallurgical enterprises; railway network; regional division; common adjacency matrix; combined degree function; regional control capability

This paper focused on the railway net areal distribution in metallurgical enterprise, proposed a network partition method which was based on common adjacency matrix and combined degree function, considerated the required train control protection ability of each sub-area. The applications of this division method in a metallurgical enterprise showed effective feedback, guided the design and planning of the range of regional control systems.

2014-05-16

陳建強，助理工程師；張昱，助理工程師。

F530.32∶TP39

A

1005-8451（2014）11-0009-07