低空立體像對的嚴密相對定向

何海清，程朋根，王晉

(1.東華理工大學 測繪工程學院，南昌 330013；2.江西省數字國土重點實驗室，南昌 330013；3.武漢大學 遙感信息工程學院，武漢 430079)

1 引 言

低空攝影測量與傳統航空攝影測量不僅飛行平臺不同，且獲取的影像數據也存在較大的差異，主要表現在影像的俯仰、翻滾、偏航角較大，可能達到甚至超過10°的差異，增加了立體像對的相對定向等空三過程中解算的困難[1-2]。而且，傳統的航空攝影測量空三解算過程中，對某些具有較小值的復雜表達式近似簡化。然而，對于大旋角像對的相對定向參數解算可能出現迭代不收斂甚至定向失敗，不適用于大旋角等低空影像處理，已無法滿足低空影像空三的需要。隨著數字化與計算機技術的發展，全自動化、高精度的低空影像相對定向等數據處理對于提高數據處理效率意義重大。

低空影像空中三角測量主要包括兩個步驟：相對定向與絕對定向。在相對定向中，連接各立體模型并構建航帶自由網，把測區內影像統一到同一坐標系下，并為區域網光束法平差提供初值。相對定向后測區影像立體模型是以像空間輔助坐標系為基準的自由坐標系模型，仍需通過絕對定向，利用地面控制點，把自由坐標轉換到地面攝影測量坐標。

低空立體像對相對定向是通過像對中兩影像同名射線的對對相交關系來建立地面立體模型。相對定向的關系式有以下兩種[3]：①單獨像對相對定向；②連續像對相對定向。在處理多個立體像對相對定向模型中大多采用連續相對定向方法。

在傳統航空攝影測量中，由于姿態角度值較小，可對基線分量近似簡化，以便于相對定向元素求解。然而，在低空攝影測量中，由于低空影像旋偏角較大，基線分量不能進行簡化，應嚴格按照表達式進行計算。

本文針對傳統相對定向方法難于滿足低空立體像對相對定向元素值高精度解算的需要，提出了低空立體像對相對定向嚴密解法，利用直接解法解算出相對定向元素的初值，代入推導出的低空立體像對相對定向誤差方程迭代精化，實現相對定向元素值嚴密解算。試驗表明，該方法能滿足低空立體像對相對定向元素值高精度地解算，具有較強的實用性。

2 連續相對定向

連續像對相對定向是以像對中左片為基準，解求出右片相對于左片運動的5個相對定向元素bv,bw,φ,ω,κ。

如圖1所示，像對中左片以S1為原點的像空間坐標系S1-U1V1W1作為參考基準，右片以S2為原點的像空間輔助坐標系為S2-U2V2W2，按共面條件列出右片坐標(u2,v2,w2)變換到左片(u1,v1,w1)的關系式為

(1)

式中，

陣9個元素表達式為：

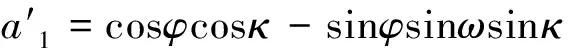
(2)

(bu,bv,bw)為S2在S1-u1v1w1中的坐標即基線向量B，其分量表達式為

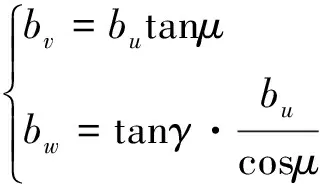
(3)

在傳統航空攝影測量中，由于μ、γ角度值較小，對分量bv、bw分別簡化為近似值buμ、buγ。然而，在低空攝影測量中，由于低空影像旋偏角較大，分量bv、bw不能進行簡化，應嚴格根據表達式進行計算。

由于式(1)為非線性函數，需對其進行泰勒展開線性化，表達式為：

(4)

其中，F0為bu,bv,bw,φ,ω,κ的初值代入式(1)中得到的函數近似值，各偏導為：

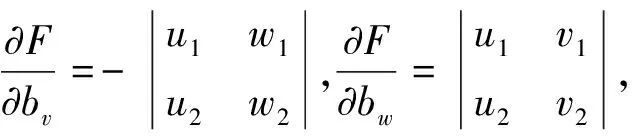
(5)

圖1 連續像對共面條件

在傳統航空攝影測量中，常把bv=bw=φ=ω=κ=0作為相對定向元素初值進行迭代運算。然而，在低空影像中相對定向元素以0作為初值的迭代運算難于近似地表達各影像旋偏角，可能會影響相對定向元素結果值的精度及迭代效率。

3 低空立體像對的嚴密相對定向

針對傳統方法難于滿足低空影像相對定向，本文提出低空立體像對相對定向嚴密解法解算相對定向元素值。首先，采用相對定向直接解[4]得到的相對定向元素作為式(4)的初值，然后代入低空立體像對相對定向誤差方程進行迭代運算，進而得到精確的相對定向元素值，相關流程如圖2所示。

在直接解中，式(1)展開得：

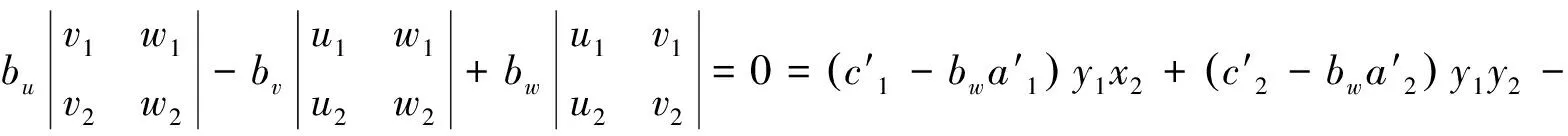
(6)

對式(6)系數用L1,L2,L3,L4,L5,L6,L7,L8,L9代替簡化表示為：

L1y1x2+L2y1y2-L3y1f+L4x2f+L5y2f-L6ff+L7x1x2+L8x1y2-L9x1f=0

(7)

式(7)兩邊同除以L5可使得9個未知參數減少為8個，其表達式為：

(8)

其中，

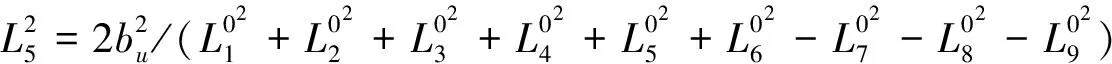
(9)

可比照李德仁[5]提出的相對定向誤差方程式，并給定基線B分量bu的值，利用式(3)計算分量bv、bw。同時引入左片與右片像點坐標(x1,y1),(x2,y2)改正數，其偏導為：

(10)

推導出低空立體像對相對定向誤差方程為：

(11)

(12)

式(11)的誤差方程可表示為：

AV=BX-L

(13)

利用最小二乘間接平差方法可得：

(14)

在解出各改正數后，代入到式(4)中進行迭代直至收斂得到最優的相對定向元素值，各參數值迭代運算表達式為：

dbv=dbv0+dbv1+dbv2+…
dbw=dbw0+dbw1+dbw2+…
dφ=dφ0+dφ1+dφ2+…
dω=dω0+dω1+dω2+…
dκ=dκ0+dκ1+dκ2+…

(15)

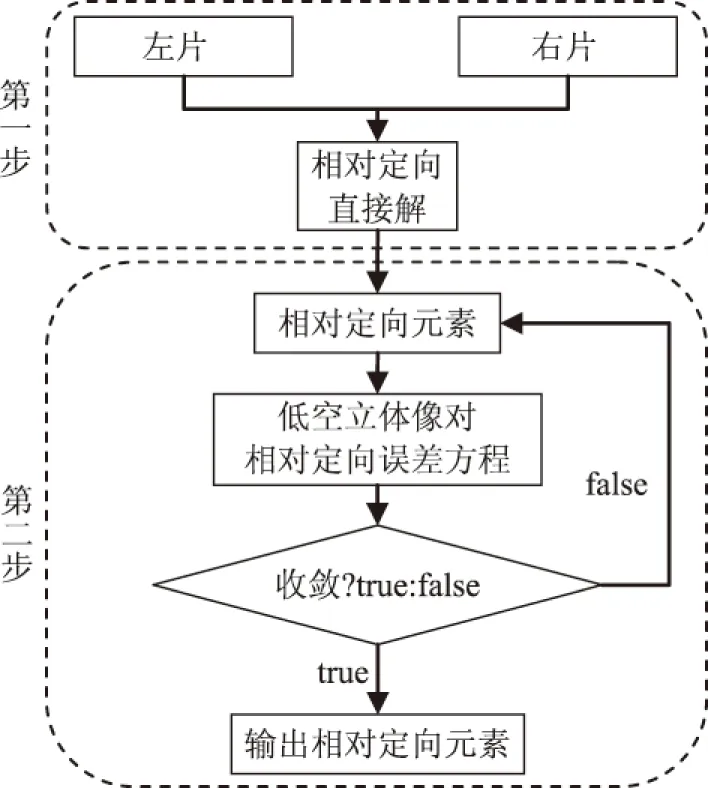
圖2 低空立體像對相對定向嚴密解法流程

4 實驗結果及分析

采用Cannon EOS 5D Mark Ⅱ相機在焦距為35.4944mm獲取的3744×5616像素及像素大小為6.4μm的低空影像立體像對進行試驗。

當前，低空立體像對大多利用計算機自動匹配點[6-8]來解算相對定向元素值。由于自動匹配得到的同名點可能存在定位誤差，為盡量減少同名點定位給試驗帶來外部誤差，本次試驗通過人工量測16個同名點來解算相對定向元素，同名點如圖3所示，拼接結果如圖4所示。同時，為了便于對比分析，對傳統連續相對定向、直接解、本文方法進行試驗，設基線B分量bu=1000，相對定向元素及上下視差如表1所示。

圖3 低空影像立體像對相對定向點

圖4 立體像對相對定向后的拼接

表1三種相對定向方法試驗對比

bubvbwφ/radω/radκ/rad最大上下視差/μm視差中誤差/μm傳統方法1000951.163720.09580.004-0.0107-0.1312.43716.3912直接解1000945.226119.12630.0051-0.0112-0.13415.57737.5462本文方法1000953.729322.00130.0043-0.0109-0.1193.78721.5337

從以上試驗對比分析可知，本文方法視差中誤差比傳統方法和直接解法相對定向小得多，精度也更高。

為進一步對比分析這三種方法，本文采用單航帶20幅影像進行相對定向后連接模型，拼接影像試驗結果如圖5所示。可見隨著航帶的變長，影像累積誤差造成的扭曲效應逐漸變大，累積誤差：直接法>傳統方法>本文方法。

圖5 三種方法單航帶拼接對比

傳統相對定向方法因初值選擇不夠準確影響解算相對定向元素的精度；直接解法不夠嚴密，未知參數Li間存在相關性，解算結果不夠穩定，也會影響相對定向結果精度；本文方法融合了傳統方法與直接解法，以直接解得到的相對定向結果作為初值，通過迭代求精的嚴密解算，在低空影像相對定向方面比傳統方法和直接解法更優。

5 結束語

針對傳統航空影像相對定向元素確定的初值難于近似地表達低空影像基線和旋偏角值，從而影響相對定向元素結果值的精度及迭代解算效率，提出了低空立體像對相對定向嚴密解法，試驗表明了該方法相對定向視差中誤差僅為傳統方法的1/4和直接解法的1/5，精度更高，對于諸如無人機、飛艇等作為平臺的低空攝影測量立體像對相對定向解算具有較強的實用性。

參考文獻：

[1] 林宗堅.多重信息多重判據影像匹配[D].武漢：武漢測繪科技大學，1987.

[2] 桂德竹.基于組合寬角相機低空影像的城市建筑物三維模型構建研究[D].徐州：中國礦業大學，2010.

[3] 王佩軍，徐亞明.攝影測量學[M].武漢：武漢大學出版社，2010.

[4] 張祖勛，張劍清.數字攝影測量學[M].武漢：武漢測繪科技大學，1996.

[5] 李德仁.解析攝影測量學[M].北京：測繪出版社，1992.

[6] 柯濤，張永軍.SIFT特征算子在低空遙感影像全自動匹配中的應用[J].測繪科學，2009，34(4)：23-26.

[7] LINGUA A，MARENCHINO D，NEX F.Performance analysis of the SIFT operator for automatic feature extraction and matching in photogrammetric applications[J].Sensors，2009，(9)：3745-3766.

[8] XING C，WANG J，XU Y.A method for building a mosaic with UAV images[J].Information Engineering and Electronic Business，2010，2(1)：9-15.