InSAR相位解纏算法在礦區沉降監測中的對比與分析

王志勇，孟慶穎

(山東科技大學 測繪科學與工程學院，山東 青島 266590)

1 引 言

隨著地下礦產資源的開采，礦區地表沉陷問題日益嚴重，在礦區形成大量的塌陷坑、塌陷槽，引起農田破壞、房屋損毀等，嚴重影響人民的生命財產安全和經濟的可持續發展。雷達干涉測量(Interferometric Sythetic Aperture Radar，InSAR)技術提供了一種全新的地表形變監測方法，具有全天候、全天時、低成本等優勢[1-6]。相位解纏是InSAR數據處理及應用的一個關鍵技術和處理步驟，特別是在InSAR礦區沉降監測數據處理中，它直接影響InSAR地表形變監測的可靠性及精確性。

InSAR技術已經初步被應用于礦區地面沉降監測中[7]，但標志性的成果還很少，尚未在礦區沉降監測中得到大規模應用，這主要是由于礦區環境的復雜性以及InSAR技術的局限性決定的。礦區形變比較特殊[7]，主要表現為沉降速率不均勻、礦區形變量非常大(如在活躍期內，一個月的沉降量可達半米，甚至更大)、沉降范圍分散；其次，沉降范圍很小(多為半徑幾百米的沉降漏斗)；礦區農田多、地表植被覆蓋率高，雷達數據相干性很差，致使在干涉條紋圖中出現很多不連續的區域。基于這些特點，部分InSAR相位解纏在礦區沉降監測中不能正確解纏，致使InSAR監測的可靠性存在很大問題。

由于不同的相位解纏算法都具有一定的適應性，并不是所有的相位解纏算法都能解決礦區大形變沉降監測時的相位解纏問題。因此，針對礦區形變的特殊性，對現有的相位解纏算法進行對比分析，探討適合礦區沉降特點的InSAR相位解纏算法，對于礦區沉降監測的可靠性及精度方面都具有十分重要的意義。

本文選取沉降特點非常明顯的濟寧市梁寶寺礦區為試驗區域，采用真實的ALOS PALSAR(日本雷達衛星，2006年發射)雷達數據，生成差分干涉圖。分別用經典的相位解纏方法進行礦區大形變區域的相位解纏實驗，并對解纏結果進行分析評價，找出適于礦區環境的、精度較高、可靠性較好的解纏方法。

2 相位解纏算法分析

所謂的相位解纏就是將相位由主值恢復為真實值的過程[2]。在InSAR數據處理中，針對相位解纏已經進行了大量的研究，提出了許多算法，主要可以概括為以下三大類[3，8-9，14]：路徑跟蹤類相位解纏算法、最小范數類相位解纏算法、基于最優估計的相位解纏算法。

路徑跟蹤類算法主要采用不同的策略尋找最優化的積分路徑，避開殘差點造成的誤差傳遞，以滿足相位梯度閉合路徑積分為零的條件，它一般是通過識別殘差點，設置正確的枝切線阻止積分路徑穿過；或者是在相位質量圖的幫助下，從高質量數據開始積分。主要包括：枝切法[10]、掩膜切線法[9]、Flynn的最小不連續法等。

最小范數類相位解纏算法是一種全局求解算法，以纏繞相位的離散偏微分與解纏相位的離散偏微分的差最小為準則建立全局的數學模型來求解相位解纏的估計值。主要包括：最小LP范數法[2-3]、高斯-賽德爾迭代法、PCG預解共軛梯度法、FFT/DCT最小二乘法、多級格網法[2-3]。

基于最優估計的相位解纏算法將最優估計的算法應用到相位解纏中，主要包括：網絡規劃法[11]、Kalman濾波法[12]、遺傳算法[13]等。

表1列出了幾種經典的相位解纏算法的核心思想以及其優缺點。

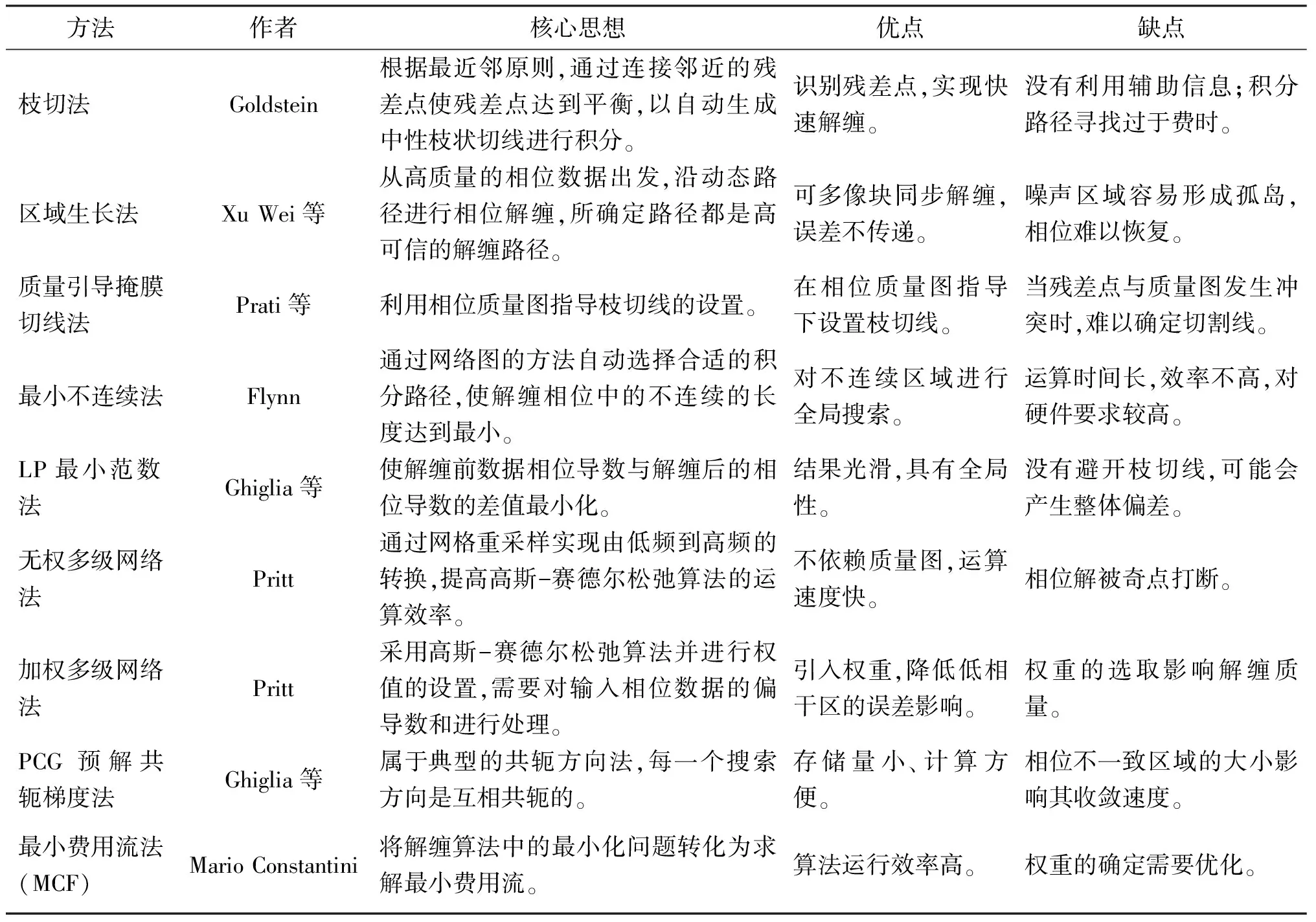
表1 相位解纏方法及特點分析

3 研究區域及InSAR相位解纏實驗

3.1 研究區域及實驗數據

選取了我國礦區地面沉降比較嚴重的濟寧礦區的梁寶寺煤礦作為實驗區，選用2009年01月10日和2009年02月25日獲取的兩景ALOS PALSAR數據組成干涉對，其path號為449，Frame號為700，其工作模式為FBS(Fine Beam Single Polarization)模式，L波段(波長23.6cm)，產品級別為Level1.1(即單視復影像數據)，HH極化，視角為34.3°，方位向像元大小為3.148m，距離向像元大小為4.684m。干涉對的垂直基線為268.542m，時間間隔46d。

除此之外，為了去除地形相位的影響，本文采用了SRTM DEM數據。

3.2 InSAR技術生成差分干涉圖

采用雙軌法差分干涉測量[7]的方法生成差分干涉圖，并采用改進的Goldstein濾波算法濾除了部分相位噪聲。為使實驗更具針對性，對原始單視復影像(SLC)進行區域裁剪，獲得單個礦區的差分干涉圖，采用1∶2(距離向：方位向)多視處理，生成的差分干涉圖的大小為：470行×481列。圖1(a)為梁寶寺礦區的濾波后的差分干涉圖，圖1(b)為相干圖。

圖1 差分干涉圖及相干圖

3.3 相位解纏對比實驗

對濾波后的差分干涉相位圖分別采用枝切法、區域生長法(Region Grow)、質量引導掩膜切線法、最小不連續法、LP最小范數法、無權多級網絡法、加權多級網絡法、PCG預解共軛梯度法、最小費用流法(minimum cost flow algorithm，MCF)進行解纏實驗，解纏結果如圖2所示。

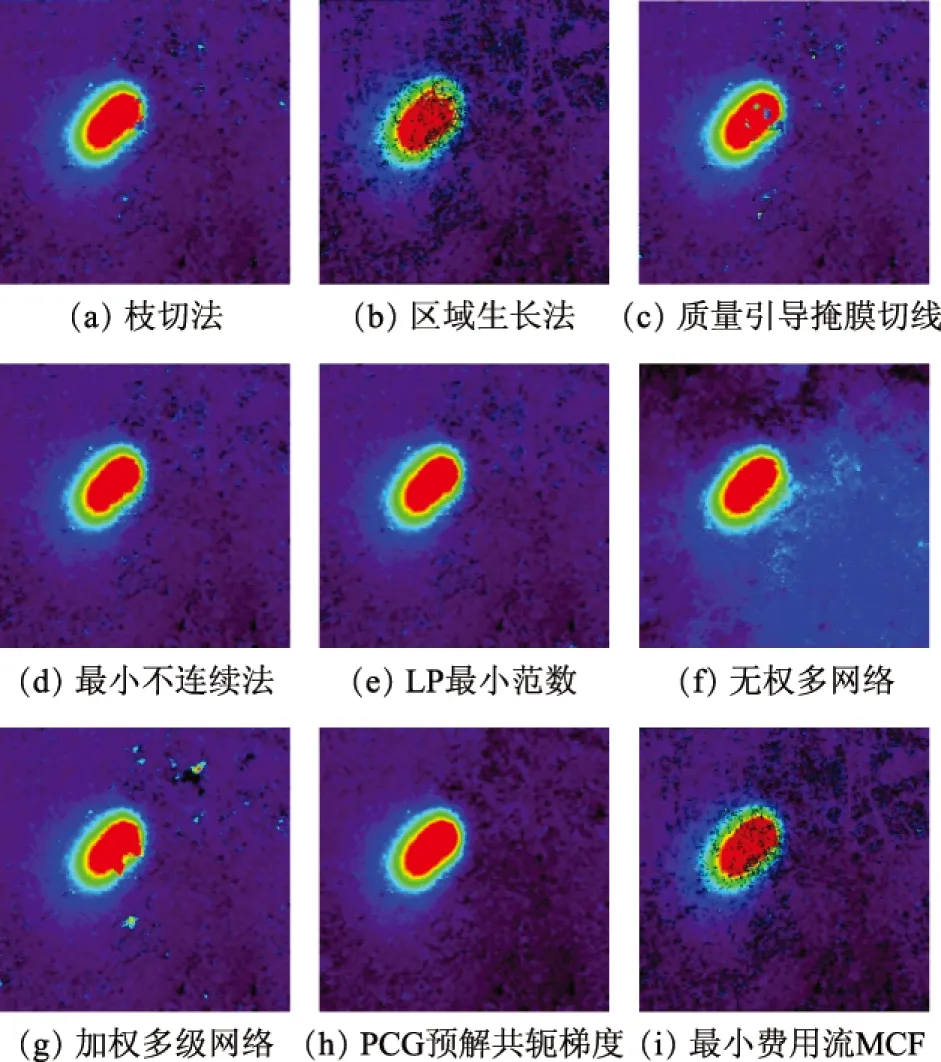
圖2 不同相位解纏方法解纏結果

4 相位解纏結果分析及評價

為了對比各種相位解纏算法在礦區沉降監測中的解纏結果，從剖面圖、統計分析、運行時間、形變量等幾個方面進行對比分析。

4.1 直接分析

根據圖2，分析不同相位解纏方法得到的解纏結果發現，基于路徑跟蹤的相位解纏算法整體效果較差，只有Flynn最小不連續法解纏效果相對較好，這是因為枝切法在相位不連續點較多且比較密集的時候，無法進行解纏，區域生長法需要從質量較好的區域開始，質量引導掩膜切線需要提供質量較好的品質圖像，礦區環境復雜，相干性較差，相位噪聲嚴重，很難滿足上述要求，只有Flynn最小不連續法可以在沒有相位質量圖指導的情況下較好地完成相位解纏；基于最小范數的相位解纏算法總體解纏效果不錯，但是加權多級網絡由于權重選擇導致其在噪聲較大的區域無法實現正確解纏；基于網絡規劃的相位解纏算法，最小費用流法(MCF)出現了較多不可解纏的區域，解纏效果較差。

4.2 剖面圖

實驗選取了其中的一行數據(位于差分干涉圖的第210行)，對比分析每種相位解纏算法的結果圖的剖面圖，所生成的剖面圖如圖3所示。

根據圖3，通過分析不同解纏方法下的剖面圖，發現枝切法、最小不連續法 、LP最小范數、加權多級網絡剖面線走勢大致相同；區域生長法、最小費用流(MCF)剖面線出現大量不連續點；質量引導掩膜切線出現突變值，形成兩個波峰，不符合整體走勢。無權多網絡、PCG預解共軛梯度雖然整體光滑，但是與其他剖面線有一定差別，可能在解纏過程中引入了誤差，導致解纏結果出現問題。

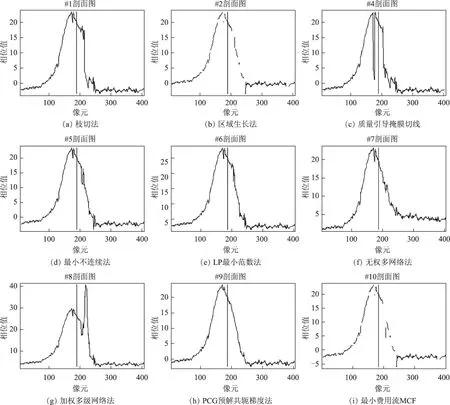
圖3 不同解纏算法的剖面圖比較

4.3 定量統計比較及運行效率對比

對各相位解纏算法得到的解纏結果進行了統計分析，分別統計了其最大值、最小值、均值及標準差等，表2列出了各種相位解纏方法的統計結果。

結果顯示加權多級網絡和LP最小范數法的平均值和標準差較大，其他方法大致接近。在運行速度上，枝切法運行時間最短，LP最小范數運行時間最長。枝切法運行速度最快，但是穩定性較差；區域生長法穩定性較好，但是運行時間過長；無權多級網絡運行較快且穩定性較好；最小不連續法在解纏效果、標準差、運行時間、直方圖形狀和剖面線走勢上比較均衡，沒有突出優勢，但是整體較好；LP最小范數穩定性一般、運行最慢，但是解纏效果較好。

本文采用的9種相位解纏算法均運行在Windows XP環境下，電腦配置為Intel(R) Core(TM)2 Duo CPU2.80GHz、4G內存。各種解纏算法運行時間如表2所示。從表2中可以看出，不同的相位解纏算法的運行時間有很大差異，其中枝切法最快，而LP最小范數法由于是一種全局最優解，其運行時間相對較長，是所有算法中最慢的一種方法。

4.4 相位解纏對形變結果的比較

以上的統計及分析還不能確定相位解纏算法在礦區大形變量解纏時的優劣，還需要考慮解纏算法可靠性的問題。

在差分干涉圖中，一個條紋代表了半個波長的形變量，因此，根據條紋的數量可以得到最大形變量的大小，通過不同相位解纏算法得到的礦區最大形變量與條紋數目直接反應的最大形變量的差值應該在較小的范圍內，表3列出了各相位解纏方法得到的最大形變量與理論值之間的差值。

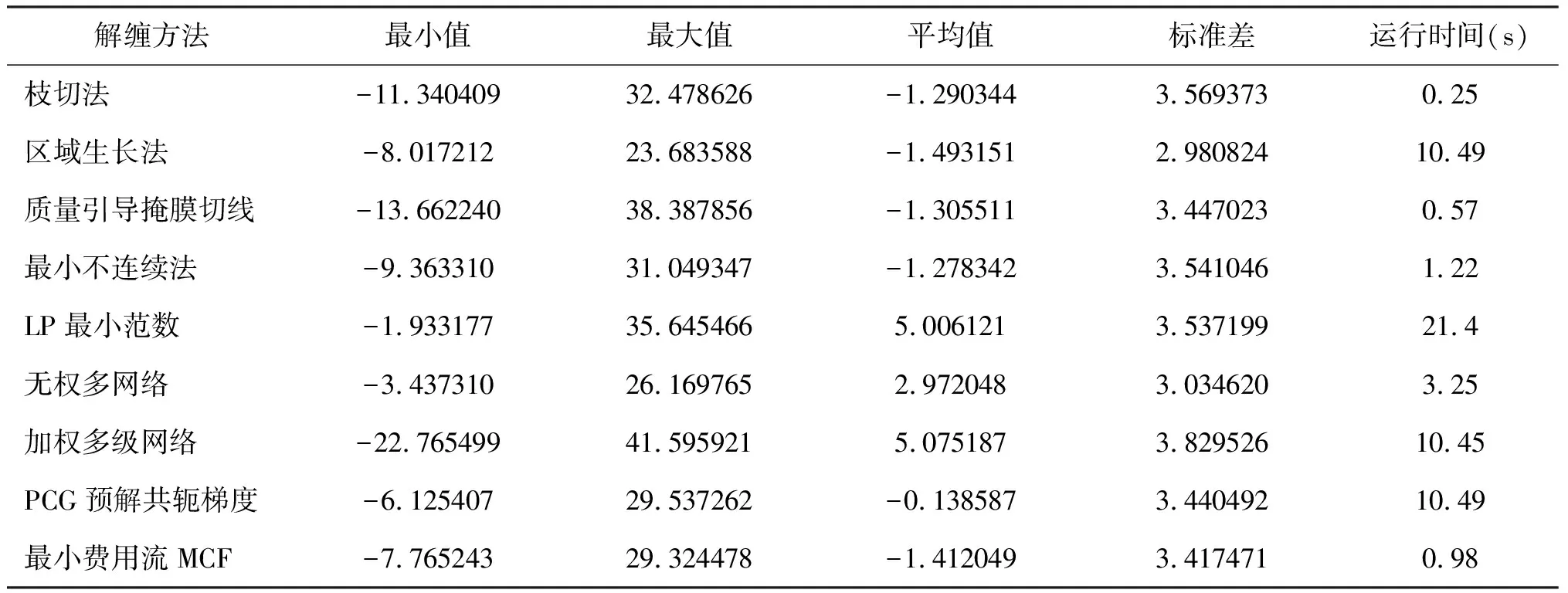
表2 相位解纏算法統計比較

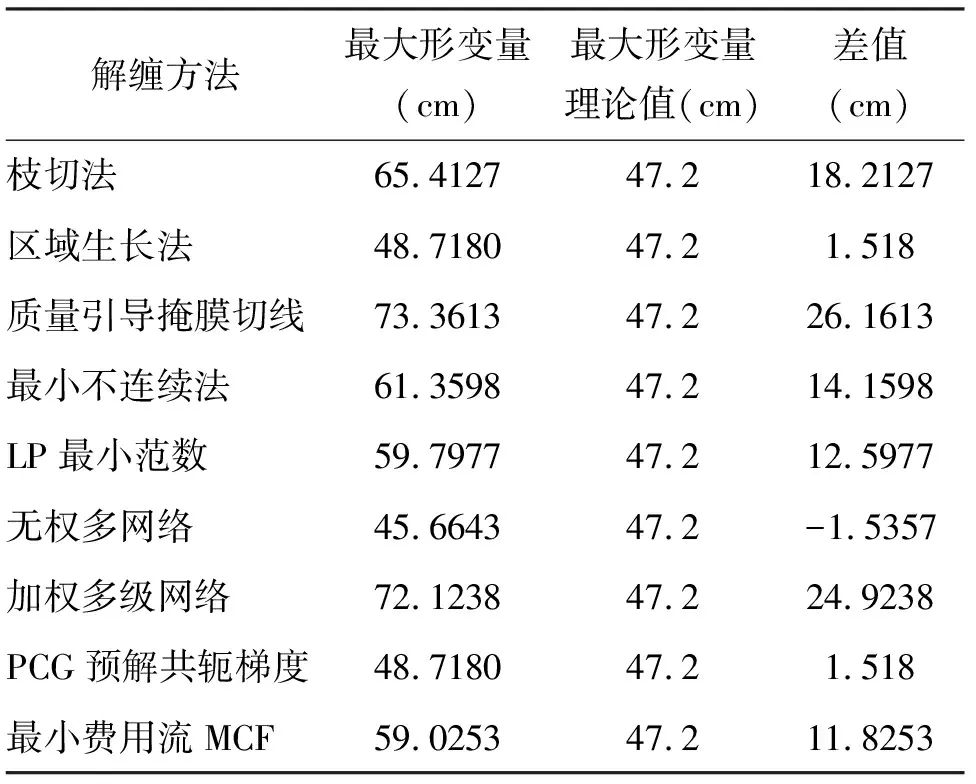
表3 各種解纏方法最大形變量與理論值的差異

從表3中可以看出，盡管所有的相位解纏算法都能恢復相位的主值并且得到形變量，但在得到的最大形變量方面卻存在較大的差異。并且有的算法與理論值相差較大，在這些算法中，區域生長法、無權多網絡算法、PCG預解共軛梯度方法得到的形變量與理論值相差較小。

通過分析各種解纏方法解纏后的形變區域的直方圖，發現區域生長法、最小費用流法(MCF)的直方圖較平滑，分布較好；枝切法、質量引導掩膜切線、最小不連續法分布雖然較好，但是零值較高；LP最小范數、加權多級網絡、PCG預解共軛梯度直方圖分布不好且有毛刺；無權多網絡出現兩個峰值。

5 結束語

對梁寶寺礦區的差分干涉圖，采用多種方法進行了解纏實驗，并對解纏結果進行了定性和定量分析，通過分析發現：在礦區環境中，最小費用流法沒有顯著優勢，反而出現了較多不可解纏的區域，而最小不連續法、LP最小范數、無權多級網絡和PCG預解共軛梯度在解纏效果相對不錯。其中PCG在解纏過程中引入誤差導致直方圖和剖面線與整體不一致，LP最小范數運行時間過長。綜合分析得出最適于用于礦區的相位解纏方法是最小不連續法和無權多級網絡法，它們解纏效率較高、精度較高，穩定性和可靠性較好，在礦區解纏實驗中，受噪聲影響較小，能較好地完成相位解纏。本文較全面地分析了在礦區環境中各種相位解纏方法的優缺點，為礦區相位解纏方法的選擇提供了依據，對礦區沉降監測精度的提高具有重要意義。

致謝：本研究還得到了山東省泰山學者建設工程專項以及山東科技大學科研創新團隊支持計劃項目(2011KYTD103)的資助，在此表示感謝。

參考文獻：

[1] HANSSEN R.Radar interferometry-data interpretation and analysis[M].Kluwer Academic Publisher，2001.

[2] 李平湘，楊杰.雷達干涉測量原理與應用[M].北京：測繪出版社，2006.

[3] 王超，張紅.星載合成孔徑雷達干涉測量[M].北京：科學出版社，2002.

[4] 張永紅，張繼賢，龔文瑜.基于SAR干涉點目標分析技術的城市地表形變監測[J].測繪學報，2009，38(6)：482-487.

[5] 程璞，許才軍，王華.InSAR相位解纏算法研究[J].大地測量與地球動力學，2007，27(3)：50-55.

[6] 黃國滿，張繼賢，趙爭，等.機載干涉SAR測繪制圖應用系統研究[J].測繪學報，2008，37(3)：277-279.

[7] 王志勇，張繼賢，黃國滿.基于InSAR技術的濟寧礦區沉降精細化監測與分析[J].中國礦業大學學報，2014，43(1)：169-174.

[8] 靳國旺，徐國華，余懋勛，等.基于瞬時頻率估計的InSAR相位解纏[J].測繪科學技術學報，2009，26(1)：33-35.

[9] GHIGLIA D C.Two-dimensional phase unwrapping：Theory，algorithms and software[M].New York：John Wiley & Sons，Inc，1998.

[10] GOLDSTEIN R M，ZEBKER H A，WERNER C L.Satellite radar interferometry：Two-dimensional phase unwrapping[J].Radio Science，1988，23(4)：713-720.

[11] CHEN C W.Statistical-cost network-flow approaches to two-dimensional phase unwrapping for radar interferometry[D].California：Standford University，2001.

[12] 劉國林，郝華東，陶秋香.卡爾曼濾波相位解纏及其與其他方法的對比分析[J].武漢大學學報(信息科學版)，2010，35(10)：1174-1178.

[13] 趙爭，張繼賢，張過.遺傳算法在InSAR相位解纏中的應用[J].測繪科學，2002，27(3)：37-39.

[14] 劉志敏，張景發，羅毅，等.InSAR相位解纏算法的實驗對比研究[J].遙感信息，2012，27(2)：71-76.